柱形料腔中超声空化效应的空间分布特性研究

俞剑，刘斌，徐雪冬，冯丽丽

柱形料腔中超声空化效应的空间分布特性研究

俞剑，刘斌，徐雪冬，冯丽丽

(北京工商大学材料与机械工程学院，北京 100048)

研究了20 kHz的圆柱形料腔中超声空化效应的形成及其空间分布特性。应用柱贝塞尔函数，推导获取了柱形声场内超声传播的声能密度的分布，并采用有限元方法进行仿真分析。针对频率为20 kHz的功率超声实验，结合声学测量方法和鲁米诺声致化学发光方法，对理论分析结果进行了验证对照。结果表明：料腔半径=50 mm，20 kHz谐振液位高度=90 mm时，若功放电流<40 mA，超声空化效应出现在变幅杆端部区域；若40 mA≤功放电流≤80 mA，空化效应显著增强，空化效应的空间分布与场内声压分布一致，空化效应受声模态影响，形成远场空化效应的分布特性；若功放电流>80 mA，受非线性因素影响，谐振液位时，空化效应在声流作用下呈柱形拖尾状分布，并在底部壁面边界形成平铺状分布；非谐振液位高度等于75 mm时，超声空化效应随功率增加仅在变幅杆端部区域出现，且呈现局域空化分布特性。

柱形料腔；空化效应；功率超声；谐振液位；鲁米诺声致化学发光法

0 引言

超声波破碎是利用声能对液体内的固体颗粒或生物组织实施破碎的过程，与传统破碎技术相比，超声破碎可获得更为均匀和细小的粒径，并具有更高的能效[1-5]。空化效应作为超声破碎中的主要作用机制，理解超声空化效应的形成，如何增强空化效应的作用范围，提高超声能效的利用已成为超声研究的重要内容[6-7]。

超声空化效应是由料液声场中的交变压力所引发，超声波的输入频率[8-11]、振幅[8,11-12]、声场条件[12-15]、料液空化阈值[11,16]是影响空化效应的直接因素。当超声波频率、料液确定时，提高超声波的输入振幅，改变声场条件是增强超声空化的有效措施。提高超声波输入振幅主要有两种途径：(1) 增大变幅杆功率输入[14]；(2) 设计高效能的变幅杆结构[17-19]。改变声场条件则考虑料腔声场的几何形状与边界条件，以获取更为高效的声能密度分布，以利于空化效应的增强[20-23]。

已有研究表明，低频功率超声具有更强的超声空化作用，现有的超声破碎机频率多采用20 kHz。本研究以频率为20 kHz的浸入式圆柱形超声破碎装置为研究对象，从声场能效增强利用的角度出发，应用柱贝塞尔函数推导获取了柱形料液场的声模态，结合谐振强化，针对20 kHz超声频率设计了柱形容器的半径和液位高度，在声学有限元分析的基础上，分析了该声场条件下的声能密度分布特性，并与非谐振液位进行了对比研究。最后采用直接声场测量与间接鲁米诺声致化学发光方法相结合(Sono Chemi Luminescent, SCL)，对理论分析结果进行了实验验证，获取超声空化效应在柱形料腔中的空间分布特性。

1 材料与方法

1.1 材料与仪器

1.1.1 材料与试剂

鲁米诺(luminol，C8H7N3O2，一种化学发光剂)，纯度98%，Ark Pharm公司；固体NaOH，纯度96%，阿拉丁工业公司；反应料液采用去离子水；半径50 mm、高度120 mm的柱形透明容器。

1.1.2 主要仪器设备

超声波处理单元构成：超声功率放大器，额定功率为200 W，变幅杆式超声换能器，输出端半径为6.5 mm，输出频率为20 kHz，中国科学院声学研究所定制；测振系统：速度型激光测振仪，速度灵敏度为200 mm·s-1，B&K公司；多通道数字示波器：TDS 2024B数字彩色示波器，测试带宽为200 MHz，采样率为2 GHz，4通道，泰克公司。

1.2 方法

1.2.1 实验方案及系统

超声波在水中传播时，产生大量空化泡，空化泡溃灭时产生的高温高压会形成光辐射现象，即“声致发光”。由于其光辐射能量较低，常温状态下肉眼难以观察。为了强化其光辐射能量，可加入微量增强剂鲁米诺(luminol)。其作用原理为超声空化气泡溃灭时产生的高温高压可水解产生羟基(OH自由基)，并与鲁米诺发生反应，羟基化的鲁米醇显示强烈的化学发光，这种现象被称为声致化学发光(SCL)[15]。发光强度由羟基数量决定，即超声空化强度大小(反映了声场能量的分布特性)决定。为了有效增加羟基数量，可在水溶液中加入适量NaOH或KOH，鲁米诺浓度宜采用0.1 g·L-1，NaOH的添加量为1 g·L-1[12]。

为观察发光现象，实验采用暗室条件，声致化学发光可形成淡蓝色的光束，肉眼可见，采用数码相机记录图片，曝光时间>3 min。料腔工况条件为：底部悬置点支撑条件，使料腔底部与料腔径向壁面的边界条件统一为软边界条件。

测试系统简图如图1所示。图中，为柱形料腔半径，为变幅杆浸入水中深度，为液位高度。

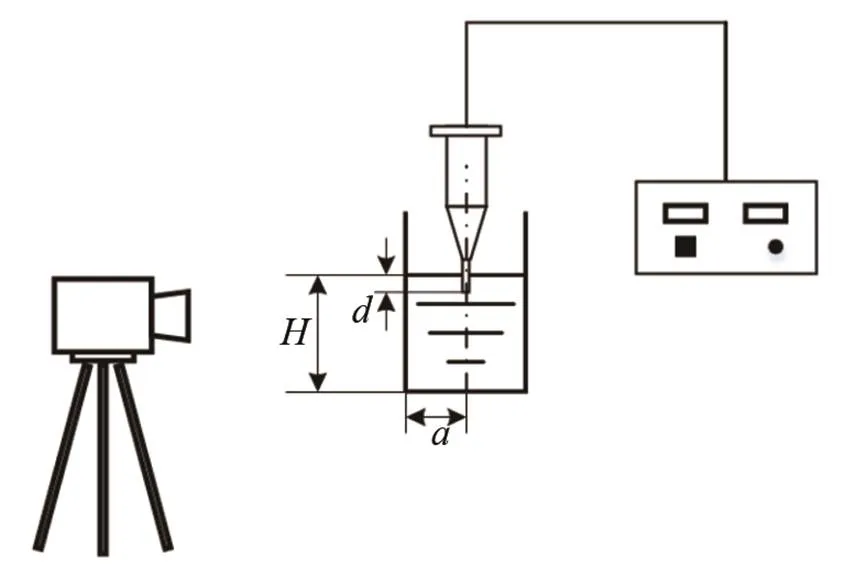
图1 测试系统简图

1.2.2 圆柱管腔内的超声传播特性

理想均质流体媒介中小振幅声波的波动方程可表示为

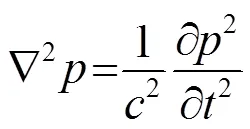
超声破碎料腔采用圆柱形管腔形式，根据水和空气的声阻抗特性及料腔壁厚，可将液体-空气界面、液体-料腔壁-空气界面均可简化为软壁面边界条件，腔内形成高次波的传播形式，声压可表示为轴向波束和径向波束的合成：

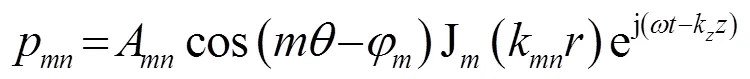
由软壁面边界条件和对称声源特性，可以得到圆柱形管腔内高次波贝塞尔函数为

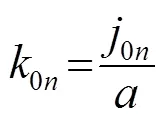
由此可得：

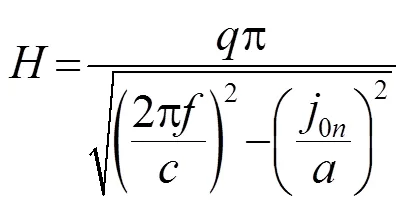
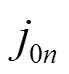
研究表明，当料液腔高度取声模态液位高度时，料液腔声场中的声能分布大大提高，由此可知，超声破碎应用中，当料腔中料液物性、边界条件、声源强度一定时，声源频率达到料腔声场的声模态频率(谐振频率)，可增强声传播能量，提高空化能利用率并有效增加空化作用范围。

1.2.3 声场有限元模型

有限元分析采用COMSOL软件。声场几何形状为圆柱形腔体，声场模型的网格划分：根据轴对称条件，可简化为轴对称二维平面，取一半进行四边形网格划分，网格最大边长为4 mm，计算上限频率约为62 kHz。传声媒介的特性取值：设定水的密度为1 000 kg·m-3，声速取1 480 m·s-1。边界条件：声源边界条件是变幅杆端部振动速度(实测值)；壁面边界条件是变幅杆侧面-料液界面为刚性壁硬边界全反射条件；料液-空气界面为软边界全反射条件；料液-玻璃壁面-空气可视为料液-空气软壁面边界全反射条件，由于20 kHz超声在中间层玻璃中的波长(纵波)约为280 mm，远大于玻璃壁厚(2 mm)，根据声波通过中间层的传播规律，玻璃层透射系数约为1，因此可忽略中间层玻璃的影响，简化为料液-空气边界条件。

2 结果与分析

2.1 声源边界条件的确定

由于声源边界条件为超声变幅杆端部振动速度，因此需获取超声变幅杆的工况频率和振速幅值作为仿真声源边界条件，以确保仿真的有效性。取功放电流为40 mA和70 mA，变幅杆端部振速幅值随频率的变化如图2所示。

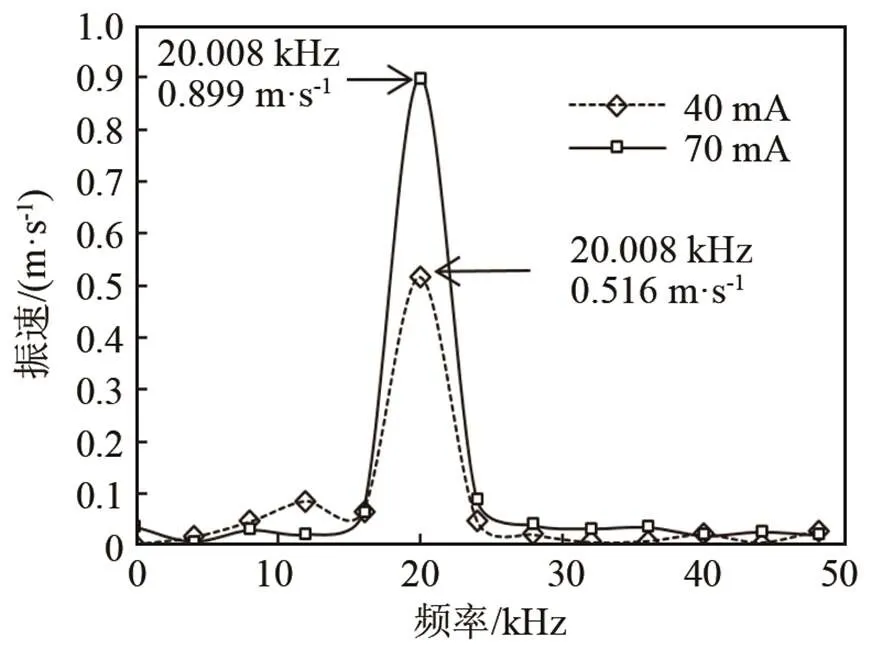
图2 声源振速频谱图

变幅杆出厂标称频率为20 kHz。由图2可知，其工况频率为20.008 kHz，频率误差为0.04%，对于20 kHz条件下模态液位计算的影响较小，对于平均声能量密度幅值及分布的量化分析计算影响可忽略。仿真分析可采用工况频率20 kHz。

图2表明，工况20 kHz频率时，变幅杆端面的纵向振动速度达到最大，超声功放电流为40 mA和70 mA时，振速分别为：0.516 m·s-1，0.899 m·s-1。

2.2 谐振料腔声场的声能分布特性

根据定容声场条件，以半径50 mm圆柱形料腔为例，取为1的柱贝塞尔函数解(高阶解时，径传播的声压幅值衰减较大)。声源工作频率20 kHz，由式(5)中的谐振液位高度计算公式，可求得轴向简正波数为=2时的液位高度=90 mm。另取一非谐振液位高度=75 mm进行对照。考察两种液位高度下声场中的声能的分布特性。

取功放电流为70 mA，变幅杆浸入料液腔深度为10mm作为声源边界条件。两种液位高度的料腔声场中的声压分布云图如图3所示。

液位高度为75 mm时，该声场条件下的一、二阶谐振频率与20 kHz偏差较大，在声源频率为20 kHz时不能形成谐振条件，场内声压分布如图3(a)所示。液位高度为90 mm时，该声场条件下谐振频率为20 kHz时，波束沿轴线方向形成2个简正波数，表现为二阶声模态特性，其声压分布呈双椭圆上下对称分布，两声压极值位置分别位于料腔高度的1/3和2/3处，对称面位于料腔高度的1/2处，且该对称面处声压为0。声压幅值远高于非谐振液位条件，且声压最大值分布表现为远离声源位置。

图3 两种液位高度下的平均声能密度

2.3 不同功放电流条件下柱形液腔中的空化分布规律

2.3.1 料腔声场的声能密度峰值特征

为了验证在谐振液位高度=75 mm和=90 mm下不同功率对超声空化效应空间分布特性的影响，功放电流取值范围为40～80 mA，增量为10 mA(变幅杆浸入料液深度为10 mm，料腔半径为50 mm，激励频率为20 kHz，液位高度为=75 mm和90 mm)，两种液位条件下料腔声场中声能密度峰值随变幅杆输入电流的变化特征如图4所示。

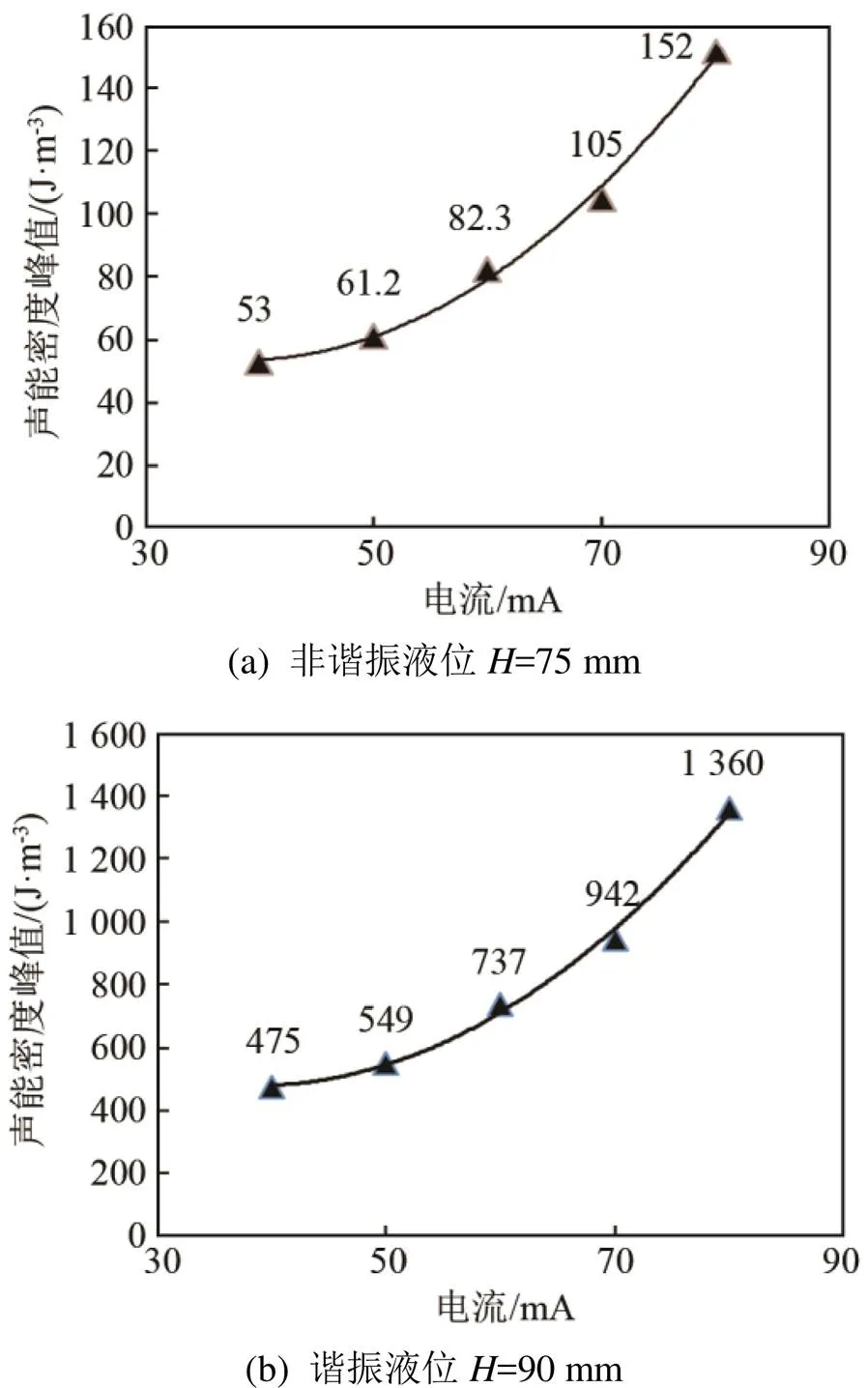
图4 不同电流下的声能密度峰值

图4中，在非谐振液位=75 mm，电流在40～80 mA的情况下，平均声能密度的空间分布不变，声能密度峰值整体较小，同时随着电流增大，声能密度峰值呈非线性增长。当柱形料腔处在谐振液位=90 mm时，电流在40～80 mA的情况下，平均声能密度的空间分布不变，声能辐射效果好，声能的辐射便最大限度地得到了提高，并且是随着电流的增大，声能密度随之增大。在谐振液位时，因柱形料腔中产生共振的现象明显，共振效果好，导致空化效应明显，声能密度较大；而非处于谐振液位时，共振效果不明显，声能密度峰值小，并且谐振液位是非谐振液位声能密度峰值的10倍左右。

为了更好地研究超声破碎空化场的效果，将鲁米诺发光实验结果与仿真分析进行比对，以获得超声空化场的能量分布特性。

鲁米诺发光实验中，变幅杆激励频率为20 kHz，功放电流范围为40～200 mA，变幅杆浸入料液深度为10 mm，料腔半径为50 mm。采用两种液位条件：非谐振液位高度为75 mm；谐振液位高度为90 mm。

2.3.2 非谐振液位料腔空化场

柱形料腔中，在非谐振液位=75 mm时，随功放电流变化，料腔场内鲁米诺发光图像如图5所示。当电流处在40～200 mA范围时，空化区域不符合线性模态分布，此时空化区域呈现非线性分布。在此阶段，随着电流变化，柱形料腔中的空化效应一直符合仿真的结果，声能密度的大小随之变化，料液中的物料在超声处理下只在变幅杆端部附近能够有效空化破碎，超声能量的转换效率比较低。非谐振液位时，声压最大值分布于变幅杆端部附近，超声空化集中作用于变幅杆端部，一方面加剧了变幅杆端部表面的金属腐蚀，另一方面使其附近料液的温迅速明显，大大降低了声能的转换效率和作用范围，不利于实际应用。实验结果验证了仿真得出的空化效应的空间分布特性。

图5 非谐振液位H=75 mm时在不同电流下的SCL图像

2.3.3 谐振液位的空化场特征

柱形料腔中，在谐振液位=90 mm时，随功放电流变化，料腔场内鲁米诺发光图像如图6所示。当电流在40～80 mA范围时，空化区域符合线性模态分布，在此阶段，随着电流变化，柱形料腔中的空化效应一直符合仿真的结果，空化区域呈现模态分布，只有声能密度的大小随之变化，谐振液位时，声压最大值表现为远离声源位置，且超声空化区域也明显增大，声能的转换效率显著提高，空化作用范围有所扩大。当功放电流继续增大，至80～200 mA时，空化区域的模态分布被破坏，呈现柱形束状分布，随着电流进一步增大，集束状的发光区域扩展至料腔底部形成平铺层状。由此推断，随功放电流增大，声源振幅的增大导致声波的非线性传播形成，出现有声流现象，不再满足小振幅声模态规律，有待后续进一步研究分析，本文不再讨论。

2.3.4 空化域分析

谐振液位=90 mm与非谐振液位=75 mm鲁米诺发光面积占比百分数柱状图如图7所示。

图6 谐振液位H=90 mm时在不同电流下的SCL图像

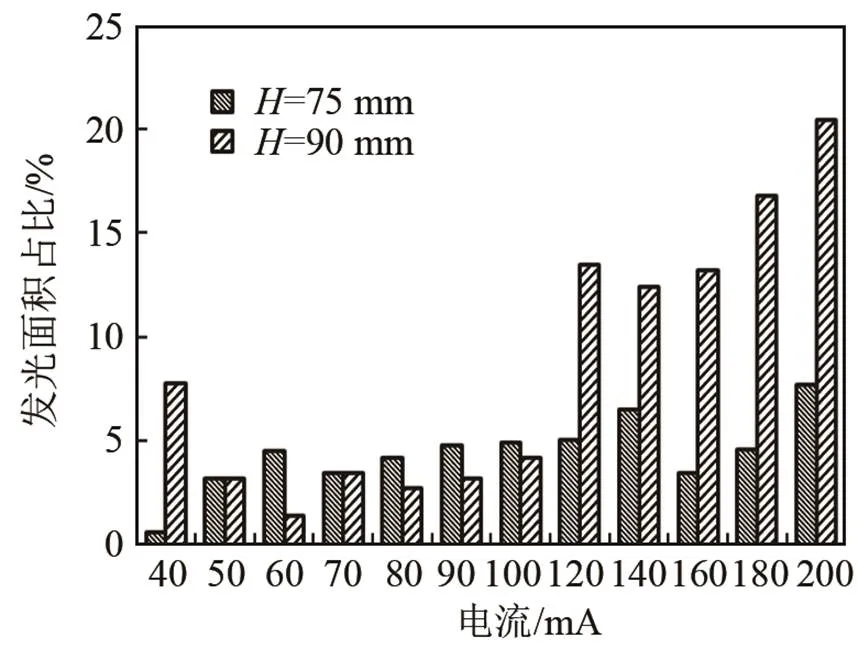
图7 谐振与非谐振液位在不同电流下发光面积占比

图7中，柱形料腔在在非谐振液位=75 mm、电流在40～200 mA时，鲁米诺发光面积占比百分数随着电流的增大而增强，在谐振液位=90 mm，电流在40～200 mA时，随着电流的增大，鲁米诺发光面积占比百分数先增大后减小，此时的空化效应效果明显。并且圆柱形料腔声场在谐振液位=90 mm时的发光面积百分比大于非谐振液位=75 mm时的发光面积百分比，即柱形料腔在谐振液位下，空化效应远强于非谐振液位，具有更高的能量转化效率。

3 结论

本文基于有限元方法进行仿真，再应用鲁米诺声致化学发光(SCL)的方法，对柱形料腔中的空化效应进行半定量测量，研究了功率和液位高度对超声空化效应的空间分布特性的影响规律，得到以下结论：

(1) 将实验方法与有限元分析相结合，研究了定容料腔声场的声模态条件下的声能分布特性。选取半径为50mm的圆柱形料腔声场，由实验获取的声源频率和振速作为声源边界条件，结合声传媒介的物料特性确定壁面边界条件，应用声波导方程获得该声场条件下的谐振液位(二阶)高度为90 mm，提供了定容料腔声场内超声波声能传播及声量转化分析的理论基础。

(2) 对于定容料腔声场而言，当容腔半径一定时，不同液位高度中声能量分布特性具有显著差异。相同声源条件下，非谐振液位声场中平均声能密度幅值有限，且声能分布集中在声源附近，作用区域有限，导致空化现象出现在变幅杆端部附近，且远场空化效应较弱；谐振液位条件下平均声能密度幅值大大增强，且分布范围扩大明显，表现为空化效应显著增强，空化作用域的空间分布呈稳定扩大趋势，且具有明显的远场空化效应。

(3) 谐振液位条件下，功率大小(即功放电流大小)也是影响声能密度幅值与空化效应空间分布特性的重要因素。功率大小对声能和空间分布特性影响显著。在低功率条件下，空化效应呈线性模态分布，超声能量转换更为高效；在高功率条件下，空化效应受声流影响呈非线性分布，空化区域呈柱形束状分布，会导致液体温升明显，壁面边界的空化腐蚀效果增强。

本文研究了超声空化效应的空间分布特性，拓展了空化效应理论的研究，为超声破碎的实际应用和化学反应器的设计优化提供了理论参考。

[1] 何明霞, 夏大祥, 王康, 等. 低频超声激励射流破碎过程模拟与实验研究[J]. 天津大学学报(自然科学与工程技术版), 2013, 46(11): 1029-1033.

HE Mingxia, XIA Daxiang, WANG Kang, et al. Jet breakup process simulation and experimental study of low-frequency ultrasonic excitation[J]. Journal of Tianjin University(Science and Technology), 2013, 46(11): 1029-1033.

[2] 冯丽丽, 刘斌, 徐雪冬, 等. 液位对超声破碎能量场的影响研究[J]. 农产品加工, 2018(4): 15-17.

FENG Lili, LIU Bin, XU Xuedong, et al. Research on the effect of liquid level on ultrasonic broken energy field[J]. Farm Products Processing, 2018(4): 15-17.

[3] 严万里, 陈晓明, 郭丽燕, 等. 超氧化物歧化酶活性测定的影响因素研究[J]. 生物学通报, 2011, 46(3): 50-53.

YAN Wanli, CHEN Xiaoming, GUO Liyan, et al. Study on the influencing factors of superoxide dismutase activity determination [J]. Bulletin of Biology, 2011, 46(3): 50-53.

[4] 郭璇, 杨艳玲, 李星, 等. 超声空化及絮体破碎过程的模拟与试验分析[J]. 中国环境科学, 2015, 35(5): 1429-1435.

GUO Xuan, YANG Yanling, LI Xing, et al. Simulation of ultrasound cavitation bubble and numerical/experimental analysis of flocs breakage process[J]. China Environmental Science, 2015, 35(5): 1429-1435.

[5] 岑为, 夏先知, 刘月祥, 等. 基于超声破碎测定聚丙烯球形催化剂强度的方法[J]. 石油炼制与化工, 2014, 45(8): 17-21.

CEN Wei, XIA Xianzhi, LIU Yuexiang, et al. Determination of spherical catalyst strength for polypropylene by ultrasonication[J]. Petroleum Processing and Petrochemicals, 2014, 45(8): 17-21.

[6] 张婵, 郑爽英. 超声空化效应及其应用[J]. 水资源与水工程学报, 2009, 20(1): 136-138.

ZHANG Chan, ZHENG Shuangying. Effect of ultrasonic cavitation and its application[J]. Journal of Water Resources and Water Engineering, 2009, 20(1): 136-138.

[7] 应崇福. 液体中的声处理应用和声空化工程[J]. 应用声学, 2006, 25(5): 261-264.

YING Chongfu. Acoustic processing in liquids and acoustic cavitation engineering[J]. Applied Acoustics, 2006, 25(5): 261-264.

[8] 崔方玲, 纪威. 超声空化气泡动力学仿真及其影响因素分析[J]. 农业工程学报, 2013, 29(17): 24-29.

CUI Fangling, JI Wei. Dynamic simulation of ultrasonic cavitation bubble and analysis of its influencing factors[J]. Transactions of the Chinese Society of Agricultural Engineering, 2013, 29(17): 24-29.

[9] 刘丽艳, 刘芃宏, 杨洋, 等. 超声频率和液位对空化场的影响[J]. 天津大学学报(自然科学与工程技术版), 2016, 49(8): 802-808.

LIU Liyan, LIU Penghong, YANG Yang, et al. Effect of ultrasonic frequency and liquid level on the cavitation field[J]. Journal of Tianjin University(Science and Technology), 2016, 49(8): 802-808.

[10] 张艾萍, 杨钊, 夏荣涛, 等. 超声频率和管型对超声空化效应的影响研究[J]. 化工机械, 2016, 43(4): 517-521.

ZANG Aiping, YANG Zhao, XIA Rongtao, et al. Influences of ultrasonic frequency and tube types on ultrasonic cavitation effect[J]. Chemical Engineering & Machinery, 2016, 43(4): 517-521.

[11] 李争彩, 林书玉. 超声空化影响因素的数值模拟研究[J]. 陕西师范大学学报(自然科学版), 2008, 36(1): 38-42.

LI Zhengcai, LIN Shuyu. Numerical simulation of the factors influencing ultrasonic cavitation[J]. Journal of Shaanxi Normal University(Natural Science Edition), 2008, 36(1): 38-42.

[12] SON Y, LIM M, KHIM J, et al. Acoustic emission spectra and sonochemical activity in a 36 kHz sonoreactor[J]. Ultrasonics Sonochemistry, 2012, 19(1): 16-21.

[13] KLÍMA J, FRIAS-FERRER A, GONZÁLEZ-GARCÍA J, et al. Optimisation of 20 kHz sonoreactor geometry on the basis of numerical simulation of local ultrasonic intensity and qualitative comparison with experimental results[J]. Ultrasonics Sonochemistry, 2007, 14(1): 19-28.

[14] ASHOKKUMAR M, LEE J, IIDA Y, et al. Spatial distribution of acoustic cavitation bubbles at different ultrasound frequencies[J]. Chemphyschem, 2010, 11(8): 1680-1684.

[15] SON Y, LIM M, ASHOKKUMAR M, et al. Geometric optimization of sonoreactors for the enhancement of sonochemical activity[J]. Journal of Physical Chemistry C, 2011, 115(10): 4096-4103.

[16] 杨日福, 丘泰球, 罗登林. 超临界CO2流体中超声空化阈值的研究[J]. 华南理工大学学报(自然科学版), 2005, 33(12): 100-104.

YANG Rifu, QIU Taiqiu, LUO Denglin. Threshold investigation of ultrasonic cavitation in supercritical fluid CO2[J]. Journal of South China University of Technology(Natural Science Edition), 2005, 33(12): 100-104.

[17] 林书玉, 鲜小军. 功率超声换能振动系统的优化设计及其研究进展[J]. 陕西师范大学学报(自然科学版), 2014(6): 31-39.

LIN Shuyu, XIAN Xiaojun. Progress and optimization design of high power piezoelectric ceramic ultrasonic vibrating system[J]. Journal of Shaanxi Normal University(Natural Science Edition), 2014(6): 31-39.

[18] 刘浩东, 胡芳友, 李洪波, 等. 功率超声技术的分类研究及应用[J]. 电焊机, 2014, 44(12): 25-29.

LIU Haodong, HU Fangyou, LI Hongbo, et al. Classification research and the application summarization of power ultrasonic technology[J]. Electric Welding Machine, 2014, 44(12): 25-29.

[19] 潘巧生, 刘永斌, 贺良国, 等. 一种大振幅超声变幅杆设计[J]. 振动与冲击, 2014, 33(9): 1-5.

PAN Qiaosheng, LIU Yongbin, HE Liangguo, et al. Design of an ultrasonic horn with high amplitude of longitudinal vibration[J]. Journal of Vibration and Shock, 2014, 33(9): 1-5.

[20] 张颖, 刘晓宙, 龚秀芬. 两个硬边界附近的声流的数值计算(英文)[J]. 南京大学学报(自然科学), 2012, 48(5): 565-571.

ZHANG Ying, LIU Xiaozhou, GONG Xiufen. Numerical calculations of acoustic streaming near two rigid planes[J]. Journal of Nanjing University(Natural Sciences), 2012, 48(5): 565-571.

[21] 刘丹晓, 周城光, 刘克. 谐振管形状对热声发动机内非线性声场的影响[J]. 声学学报, 2012(1): 36-44.

LIU Danxiao, ZHOU Chengguang, LIU Ke. Influence of resonator shape on nonlinear acoustic field in a thermoacoustic engine[J]. Acta Acustica, 2012(1): 36-44.

[22] 魏鑫, 吴胜举, 许昊, 等. 槽壁边界对超声清洗声场特性的影响[J]. 陕西师范大学学报(自然科学版), 2012, 40(3): 48-51.

WEI Xin, WU Shengju, XU Hao, et al. Influence of tank wall boundary on characteristics of sound field in ultrasonic cleaning[J]. Journal of Shaanxi Normal University(Natural Science Edition), 2012, 40(3): 48-51.

[23] 郭策, 祝锡晶, 王建青, 等. 超声场下刚性界面附近溃灭空化气泡的速度分析[J]. 物理学报, 2016, 65(4): 180-187.

GUO Ce, ZHU Xijing, WANG Jianqing, et al. Velocity analysis for collapsing cavitation bubble near a rigid wall under an ultrasound field[J]. Acta Physica Sinica, 2016, 65(4): 180-187.

Study on the spatial distribution of ultrasonic cavitation effect in cylindrical reactor

YU Jian, LIU Bin, XU Xuedong, FENG Lili

(College of Material and Mechanical Engineering, Beijing Technology and Business University, Beijing 100048, China)

The formation and spatial distribution of ultrasonic cavitation in the cylindrical reactor of 20 kHz are studied. The distribution of the acoustic energy density in the cylindrical sound field is obtained by using Bessel function, and the finite element method is used for simulation analysis. By combining the acoustic measurement method and the sono-chemi luminescent (SCL) method, the theoretical analysis results are verified in the power ultrasonic experiment of 20 kHz. The results show that the ultrasonic cavitation effect appears in the end region of the horn when the cavity radius is=50 mm, the resonant liquid level of 20 kHz is=90mm and the current of Power Amplifier is <40 mA, in the case of 40 mA ≤ the current of Power Amplifier ≤ 80 mA, the cavitation effect is significantly enhanced; that the spatial distribution of the cavitation effect is consistent with the distribution of sound pressure in the field, the acoustic modes affect the cavitation effect to form the distribution characteristics of the far-field cavitation effect, and when the current of Power Amplifier is >80 mA, due to nonlinear factors, the cavitation effect is distributed in a cylindrical tail shape under the action of the acoustic flow at the resonant liquid level, and a tile-like distribution is formed at the boundary of the bottom wall; and that for the non-resonant liquid level of 75 mm, with the increase of power, the ultrasonic cavitation effect appears only in the end region of the horn and presents the local cavitation distribution characteristics.

cylindrical rector; ultrasonic cavitation; power ultrasonic; resonance liquid level; sono chemi luminescent (SCL)

O426

A

1000-3630(2020)-02-0127-07

10.16300/j.cnki.1000-3630.2020.02.001

2019-05-05;

2019-07-12

国家重点研发计划资助(2016YFD0400305)、北京市自然科学基金-市教委联合资助项目资助(KZ201810011017)

俞剑(1995－), 男, 安徽芜湖人, 硕士研究生, 研究方向为噪声与振动控制。

刘斌,E-mail: liubin@th.btbu.edu.cn