基于简化毕肖普法对生活垃圾土堆体边坡稳定性影响因素的影响度分析研究*
2020-05-09孙春光冯银均骆振中
孙春光,冯银均,骆振中,牟 杰
(浙江省安全生产科学研究院,浙江省安全工程与技术研究重点实验室,浙江 杭州 310012)
1 引言
卫生填埋法是目前处理生活垃圾的主要手段之一,由于近年来生活垃圾产生量急剧增加,各填埋场大多采取超量扩容填埋的应对措施。经过多地调研发现,很多填埋场扩容导致垃圾堆体增高、坡度变陡,可能造成垃圾堆体边坡失稳,从而导致发生滑坡、崩塌等事故的风险大大增加。
由于垃圾堆体边坡经长达几十年的填埋形成,垃圾成分复杂且垃圾土强度参数严重不均一,致使各垃圾堆体边坡物理力学性质差别巨大,决定了该类边坡工程的稳定性有很大的不确定性。除此之外,物理模型的不同和破坏机理同样存在不确定性,因此很难准确分析该类边坡的实际稳定性情况。垃圾堆体边坡稳定性分析的特点在于从分析之初就考虑这些不确定性,利用概率的方法统计边坡失稳破坏的可靠度和概率。在垃圾堆体稳定性影响分析方面,方玲等[1]综合考虑了影响垃圾堆体边坡稳定性的多种因素,通过数值模拟计算得到稳定性的适当参数值。Babu 等[2]研究垃圾埋龄不同造成的强度参数不同,对其进行分层分析边坡的稳定性。刘华丽等[3]利用模糊数学法研究边坡稳定性影响因素,分析稳定性强度。
由于我国与国外在文化、经济、生活上的差异,产生的垃圾土成分并不相同,处置垃圾的方法和工艺也有较大的差别,把国外垃圾土的物理力学指标直接用于我国垃圾填埋场的设计和施工欠合理,有必要对我国垃圾土进行分析研究[4]。本研究通过对我国研究学者获得的垃圾土内摩擦角、内聚力、容重等力学性质参数测值进行分析,并调研了浙江省大部分的垃圾填埋场堆体边坡几何情况,获取边坡现状的平均几何参数,建立垃圾土边坡稳定性分析模型。通过简化毕肖普分析法对垃圾堆体边坡稳定性的主要影响因素进行影响度分析,通过分析影响因素的变化对堆体边坡的稳定性影响度,为垃圾堆体边坡失稳的治理提供参考。
2 分析方法和模型建立
2.1 简化毕肖普法
依据现行的GB 50869—2013 生活垃圾卫生填埋处理技术规范13.3.3 条要求,填埋堆体边坡的稳定性计算宜按现行国家标准GB 50330—2013 建筑边坡工程技术规范中土坡计算方法的有关规定执行。GB 50330—2013 要求计算土质边坡、极软岩边坡、破碎或极破碎岩质边坡的稳定性时,可采用圆弧形滑面,并推荐使用毕肖普法分析计算。
该方法是对边坡沿纵向细分为多个切块,其假定相互条块间无剪切力,受力情况只作用于水平方向,分析条块受力情况,在抗滑力中引入安全系数,通过稳定性安全系数大小来表征边坡的稳定性。图1 为毕肖普法土条受力简图,式(1)为简化毕肖普法计算公式。

图1 毕肖普法土条受力简图

式中:ci为内聚力,φi为内摩擦角,FS为稳定性安全系数,li为条块滑动面长度,Wi为土条重力,ΔHi为受到的切向力,θi为法向夹角。
2.2 分析数值模型的建立
根据简化毕肖普法可知影响垃圾土堆体边坡稳定性的主要影响因素有:垃圾土的重力密度、内摩擦角、内聚力等垃圾土的工程特性;边坡高度、边坡比等堆体边坡几何因素。
通过对浙江省部分垃圾填埋场实地调研获取边坡高度和边坡比的数据,如表1 所示。

表1 浙江省部分垃圾填埋场边坡高度和边坡比现状
根据堆体边坡的几何样本,通过正态分布考虑,计算得到堆体高度(去除天子岭堆体高度数据) 均值μ 为44 m,标准差为16;边坡比均值μ为0.50(即1∶2),标准差为0.10。
垃圾土的工程特性主要由2 种方法获取,第1种为现场勘探采样,再进行试验测定,第2 种由原有研究测量成果获取。由于垃圾土与普通的土坡土最大的区别在于单个样本的随机性很大,每个样本获得的工程特性参数差别很大,没有相当多的总样本数,所获得的工程特性参数意义不大。作者通过第2 种方法,利用原有研究人员测得的垃圾土工程参数(表2) 进行分析利用。
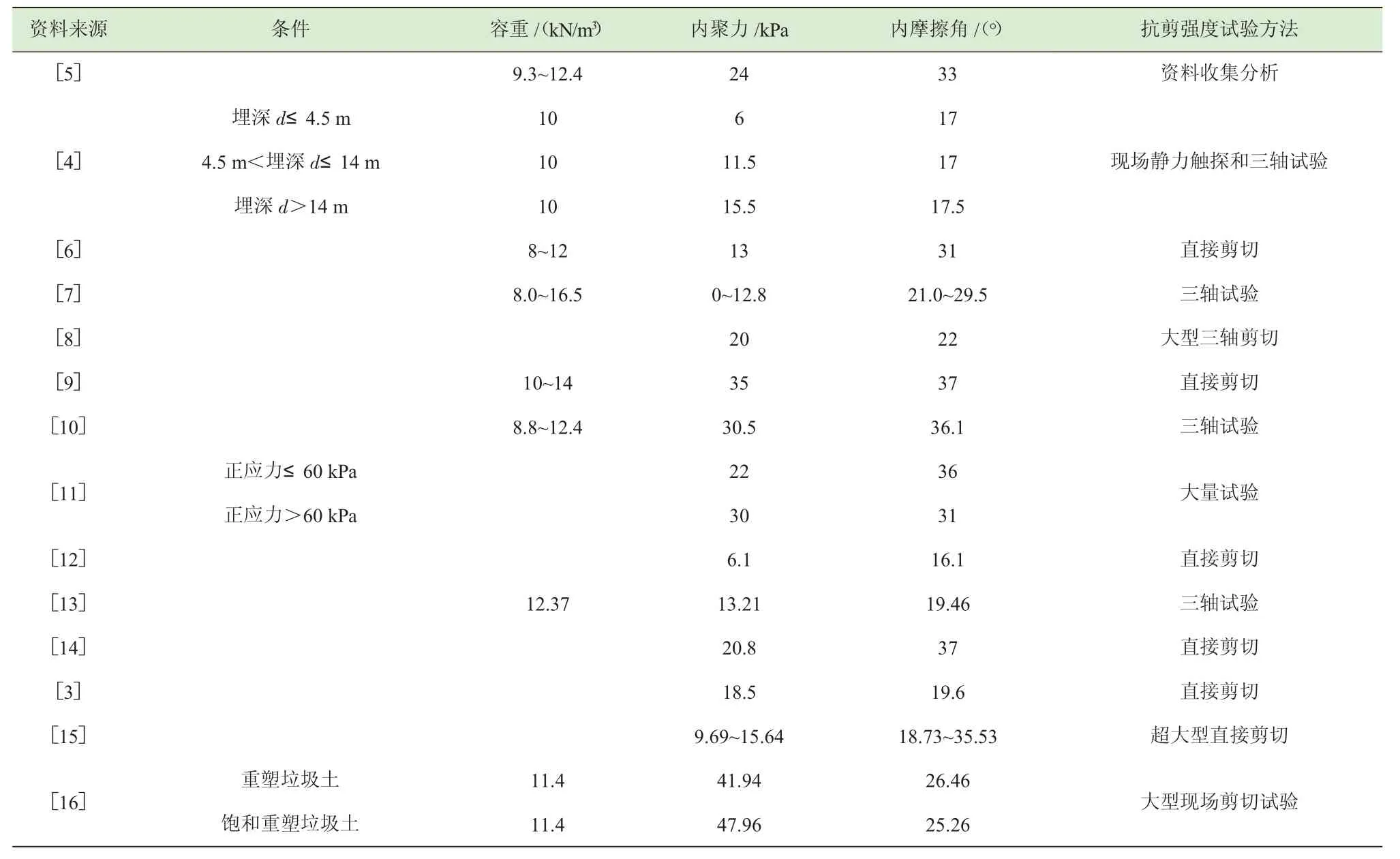
表2 收集的稳定性影响因素的数值
获得的容重、内聚力、内摩擦角等数值通过正态分布分析,得出容重均值为11.2 kN/m3,标准差为0.9;内聚力均值为22.3 kPa,标准差为12.2;内摩擦角均值为28°,标准差为6.9。
采用偏度- 峰度检验法分别对样本中的堆体高度、边坡比、容重、内聚力、内摩擦角等数值是否符合正态分布进行检验:取α=0.1,查得Ζα/4=Ζ0.025=1.96,故拒绝域为u1≥1.96 或u2≥1.96;分析计算堆体高度样本数值的u1=1.78 <1.96,u2=1.65<1.96;分析计算边坡比样本数值的u1=1.27<1.96,u2=1.16<1.96;分析计算容重样本数值的u1=1.01<1.96,u2=1.12<1.96;分析计算内聚力样本数值的u1=1.85<1.96,u2=1.72<1.96;分析计算内摩擦角样本数值的u1=1.72<1.96,u2=1.84<1.96;故可认为堆体高度、边坡比、容重、内聚力、内摩擦角等样本数值服从正态分布。
根据上述参数建立一个垃圾填埋场边坡稳定性分析模型,具体参数如表3 所示,依据参数得到边坡的横截面几何形状如图2 所示。

表3 分析模型参数

图2 模型边坡的横截面几何形状
3 稳定性分析
3.1 最危险圆弧面的确定
依据费伦纽斯法经验表,得到本模型的β1为25°,β2为35°。依据费伦纽斯法和简化毕肖普法分析安全系数,获得模型堆体边坡最危险滑动圆弧和圆心,见图3。

图3 模型堆体边坡最危险滑动圆弧和圆心
3.2 稳定性分析计算
依据简化毕肖普法,首先对模型最危险滑动圆弧宽度等分成10 个条块,做重力线OB,获得每一块与OB 的法向夹角见图4。垃圾土容重为11.2 kN/m3,并测得每块条块的面积和圆弧长度,如表4 所示。
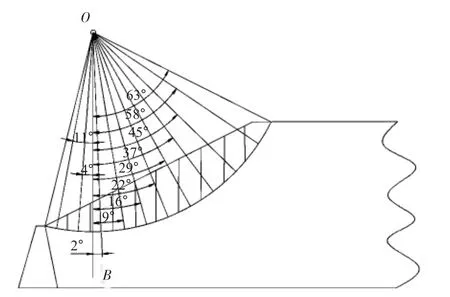
图4 最危险滑动圆弧条块划分

表4 条块法向夹角、面积和圆弧长度
假设FS=1,代入式(2) 得到:mθi={0.88,0.96,1.07,1.11,1.13,1.14,1.12,1.08,1.01,0.93};内聚力c 为22.3 kPa,内摩擦角φ 为28°,代入式(1) 得到FS=1.322。再次代入式(2) 得到:mθi={0.90,0.97,1.05,1.08,1.11,1.11,1.08,1.04,0.97,0.975,0.89},代入式(1) 得到FS=1.426。再次代入式(2) 得到:mθi={0.91,0.97,1.05,1.07,1.10,1.11,1.06,1.07,1.00,0.92},代入式(1)得到FS=1.431。通过3 次迭算,边坡安全系数FS已很接近真值,模型边坡安全系数为1.431。
4 稳定性影响因素的影响度分析
4.1 边坡高度对稳定性影响分析
根据2.2 节获得堆体高度均值μ 为44 m,标准差为16。选取1 个标准差内等分11 个样本数{28.0,31.2,34.4,37.6,40.8,44.0,47.2,50.4,53.6,56.8,60.0},在其他模型参数不变的情况下,该11 个样本数通过第3 节稳定性分析计算方法,分别分析计算获得边坡安全系数FS,如表5所示,图5 为边坡高度与安全系数影响度关系,可以看出安全系数随着边坡高度的增加而降低,边坡高度每增加0.2 个标准差,安全系数约降低0.011。

表5 边坡高度样本数与其对应的边坡安全系数

图5 边坡高度对安全系数的影响
4.2 边坡比对稳定性影响分析
根据2.2 节获得边坡比均值μ 为0.50,标准差为0.10。选取1 个标准差内等分11 样本数{0.40, 0.42, 0.44, 0.46, 0.48, 0.50, 0.52,0.54,0.56,0.58,0.60},在其他模型参数不变的情况下,该11 个样本数通过第3 节稳定性分析计算方法,获得安全系数如表6 所示,图6 为边坡比与安全系数影响度关系,可以看出边坡安全系数随着边坡比的增加而降低,边坡比每增加0.2 个标准差,安全系数降低0.077。

表6 边坡比样本数与其对应的边坡安全系数
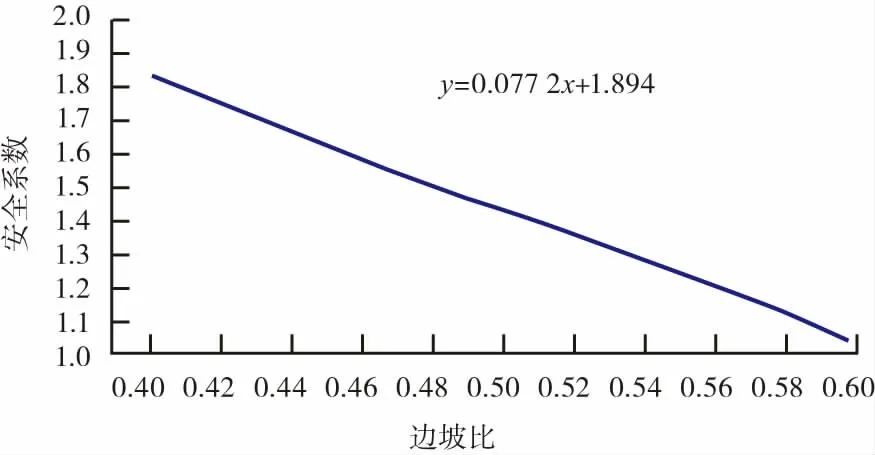
图6 边坡比对安全系数的影响
4.3 容重对稳定性影响分析
根据2.2 节获得容重均值μ 为11.2 kN/m3,标准差为0.9。选取1 个标准差内等分11 样本数{10.30, 10.48, 10.66, 10.84, 11.02, 11.20,11.38,11.56,11.74,11.92,12.10},在其他模型参数不变的情况下,该11 个样本数通过第3 节稳定性分析计算方法,获得安全系数如表7 所示,图7 为容重与安全系数影响度关系,可以看出边坡安全系数随着容重的增加而降低,容重每增加0.2 个标准差,安全系数降低0.010。

表7 容重样本数与其对应的边坡安全系数

图7 容重对安全系数的影响
4.4 内聚力对稳定性影响分析
根据2.2 节获得内聚力均值μ 为22.3 kPa,标准差为12.2。选取1 个标准差内等分11 样本数{10.10, 12.54, 14.98, 17.42, 19.86, 22.30,24.74,27.18,29.62,32.06,34.50},在其他模型参数不变的情况下,该11 个样本数通过第3 节稳定性分析计算方法,获得安全系数如表8 所示,图8 为内聚力与安全系数影响度关系,可以看出边坡安全系数随着内聚力的增大而增大,内聚力每增加0.2 个标准差,安全系数增加0.050。

表8 内聚力样本数与其对应的边坡安全系数

图8 内聚力对安全系数的影响
4.5 内摩擦角对稳定性影响分析
根据2.2 节获得内摩擦角均值μ 为28°,标准差为6.9。选取1 个标准差内等分11 样本数{21.10,22.48,23.86,25.24,26.62,28.00,29.38,30.76,32.14,33.52,34.90},在其他模型参数不变的情况下,该11 个样本数通过第3 节稳定性分析计算方法,获得安全系数如表9 所示,图9 为内摩擦角与安全系数影响度关系,可以看出边坡安全系数随着内摩擦角的增大而增大,内摩擦角每增加0.2 个标准差,安全系数增加0.059。

表9 内摩擦角样本数与其对应的边坡安全系数

图9 内摩擦角对安全系数的影响
4.6 各影响因素的影响度比较结果
根据简化毕肖普分析法对边坡稳定性主要影响因素(边坡高度、边坡比、容重、内聚力、内摩擦角) 进行安全系数影响度分析,在1 个标准差范围内,每增加或减少0.2 个标准差,影响因素的影响度排序为:边坡比(0.077) >内摩擦角(0.059) >内聚力(0.050) >边坡高度(0.011) >容重(0.010)。
5 结论与展望
1) 浙江省垃圾填埋场垃圾堆体边坡稳定性影响因素数值范围:边坡高度为28~60 m,边坡比为1∶2.5~1∶1.7(即边坡角度21.8°~31.0°),堆体容重为10.3~12.1 kN/m3,内摩擦角为21.10~34.9°,内聚力为10.1~34.5 kPa。
2) 依据简化毕肖普分析法对各影响因素的影响度进行分析,得到对边坡稳定性影响度。其中边坡比对边坡稳定性影响最大,内摩擦角和内聚力影响度其次,边坡高度和容重对边坡稳定性影响较小。故在预防边坡失稳塌滑控制措施中,减小边坡比、增大内摩擦角和内聚力是较为有效的方法。
3) 生活垃圾堆体边坡稳定性影响因素与安全系数关系:边坡比增加0.02 时(0.2 个标准差,下同),边坡安全系数降低约0.077;内摩擦角每增加1.38°,边坡安全系数增加约0.059;内聚力每增加2.44 kPa,边坡安全系数增加约0.050;边坡高度每增加3.2 m,边坡安全系数降低约0.011;容重每增加0.18 kN/m3,边坡安全系数降低约0.010。
4) 基于简化毕肖普法进行稳定性影响因素的分析,未能对其他影响因素如淋滤液水位和降解产气压力等开展研究,需今后进一步分析。
