奇异值分解提取阵列声波时差的改进方法

李鹏举, 吴昀朔, 任 莉

(1.东北石油大学 地球科学学院, 黑龙江 大庆 163318; 2.东北石油大学 非常规油气成藏与开发省部共建国家重点实验室培育基地， 黑龙江 大庆 163318; 3.中国石油集团测井有限公司 大庆分公司解释评价中心， 黑龙江 大庆 163000)

0 引 言

多极子阵列声波测井是20世纪90年代和21世纪初出现的一种极具前景的地球物理测井技术，是目前应用较为广泛的现代测井方法之一[1-2]。多极子阵列声波全波列波形曲线中包含纵波、横波、斯通利波等丰富的曲线信息，这些信息可用于裂缝识别及评价、岩层渗透性评价、油气层识别评价和地层各项异性分析等，因而很有必要提高提取时差信息的精度[3]。由于声波全波列波形曲线主要是由纵波、横波、伪瑞利波和斯通利波等四种组分波及随机噪声组成，各组分波不仅在时间上有分离现象，在频率上也是分离的，且纵波与横波都有它们的固有频率，即各组分波都有其自身的相似性[4]。早期声波测井数据处理方法主要是阈值法，这种方法的缺点是在有噪声脉冲存在的情况下首波检测容易出错[5-6]。后期Kimball与Marzetat提出了时差—时间相关分析法—STC方法[7-8]，该方法对速度接近的一些波组分的分辨力有限,并且该方法对波列中较弱的成分灵敏度较低[9]。因此，笔者采用奇异值分解法提取声波时差，利用改进后的奇异值分解法进行阵列声波数据处理，以提高时差提取的精度。

1 阵列声波时差的提取原理

奇异值分解作为一种在工程理论中获得广泛应用的数学方法，其具有很明显的物理意义。奇异值分解方法在处理占据大量储存空间并且十分复杂的矩阵时具有极大优势，用几个结构简单占据储存量小的子矩阵相乘来对原始矩阵进行表示，且对原始矩阵的重要的特性进行详细描述。

一组由n条波形曲线组成的全波列声波测井记录，每条波形曲线的采样点数为m，将这组数据转化为二维数组由矩阵X表示，其中各元素为xij，即：

(1)

矩阵X的奇异值分解等式可表示为

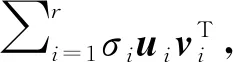
(2)

式中：U——方阵XXT的m×r阶特征向量(ui)矩阵；

V——方阵XTX的n×r阶特征向量(vi)矩阵；

Λ——对角线矩阵，矩阵中各个元素为矩阵X的奇异值σi(XXT或XTX的非负平方根)，各个元素按递减顺序，Λ=diag(σ1,σ2,…,σi);

r——矩阵X的秩。

矩阵XXT(或XTX)为协方差矩阵，由于协方差矩阵所具有的正定性质，使矩阵XXT(或XTX)的特征值为实数且为非负数，因此，矩阵X的奇异值一定是存在的[10]。

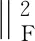
(3)

式中：XP——当第P项至最后一项奇异值σP+1，σP+2，…，σN取零值时的重构矩阵，即XP=U·ΛPVT，其中ΛP=diag(σ1,σ2,…,σP,0,…,0)；

‖X‖F——矩阵X的F范数[11-12]。

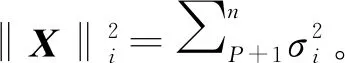
2 改进的阵列声波时差提取方法

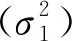
(4)

2.1 子空间类算法

通过奇异值分解算法得到的奇异值矩阵主对角线元素σk是按递减顺序排列的，奇异值矩阵主对角线元素σk从首项开始对相邻2项依次进行差分得到梯度序列为

B(k)=σk-σk+1，(k=1,2,…,M-5),

(5)

式中,B(k)——差分梯度序列第k个元素。

算法的基本原理为寻找梯度序列每一项元素与后5项元素之和的比值序列A(k)的最大值，并将最大值的序列号k作为空间分界点

(6)

根据性质0≤A(k)≤1，当A(k)最大时，其k值代入式(7)便可对信噪比进行优化，

(7)

式中：σSi——奇异值中有用信号部分；

σN——奇异值中无用信号部分。

2.2 加权函数法

在得到用于时差提取的信噪比αSNR后，将αSNR加一个加权函数，从而突出有用αSNR，提高时差提取的准确性。

加权函数为

(8)

加权后的信噪比为

βGSNR=ρ·αSNR，

(9)

3 实际测井数据的处理

为验证改进后的奇异值分解提取阵列声波时差方法的实际应用效果，应用子空间类奇异值分解算法对玛湖油田玛十八井区某井XMAC阵列声波数据进行实际处理。

3.1 子空间类奇异值分解法时差提取步骤

步骤一利用拉格朗日插值法，在每两个记录点之间插入五个点，将时间采样间隔由原来12 μs变为2 μs，大大提高了处理精度。

步骤二在实际测量过程中，测井声系的选取由所测井段实际地层情况来决定。时窗宽度Tw的一般选取原则为：选取某种待检测模式波的理论长度作为时窗宽度。Tmin和Tmax分别代表任意一条波形曲线所含有有用信号的最小时间与最大时间；ΔTb、ΔTe、δT三个变量分别代表相邻接收探头间波形曲线的扫描时差ΔT的起始值、终止值和增量。

步骤三将一组声波全波列波形数据以T=Tmin为时窗中心，以ΔTb为扫描时差ΔT的起始值，以Tw为时窗宽度形成二维数据X。对得到的矩阵XXT或XTX进行奇异值σi的计算，随后计算信噪比αSNR，并对其进行优化，优化后的信噪比βGSNR为相邻波形曲线相似性的度量。

步骤四令ΔT=ΔTb+δT·i(i=1,2,…)，重复步骤二,直到ΔT=ΔTe为止,得到一条以Tmin为参数的ΔT-GSNR曲线。

步骤五令T=Tmin+(Tw/2),重复步骤二、步骤三，得到以Tmin+(Tw/2)为参数的ΔT-βGSNR曲线，如图1所示。

步骤六令T=Tmin+(Tw/2)·j(j=2,3,…)，重复步骤二、三、四，直到T=Tmax为止，将得到的曲线合成绘制成βGSNR与ΔT、T的函数关系，如图2所示，函数关系图的峰值对应的时差值作为时差结果进行输出。

图1 时差提取步骤Fig. 1 Extract interval transit time

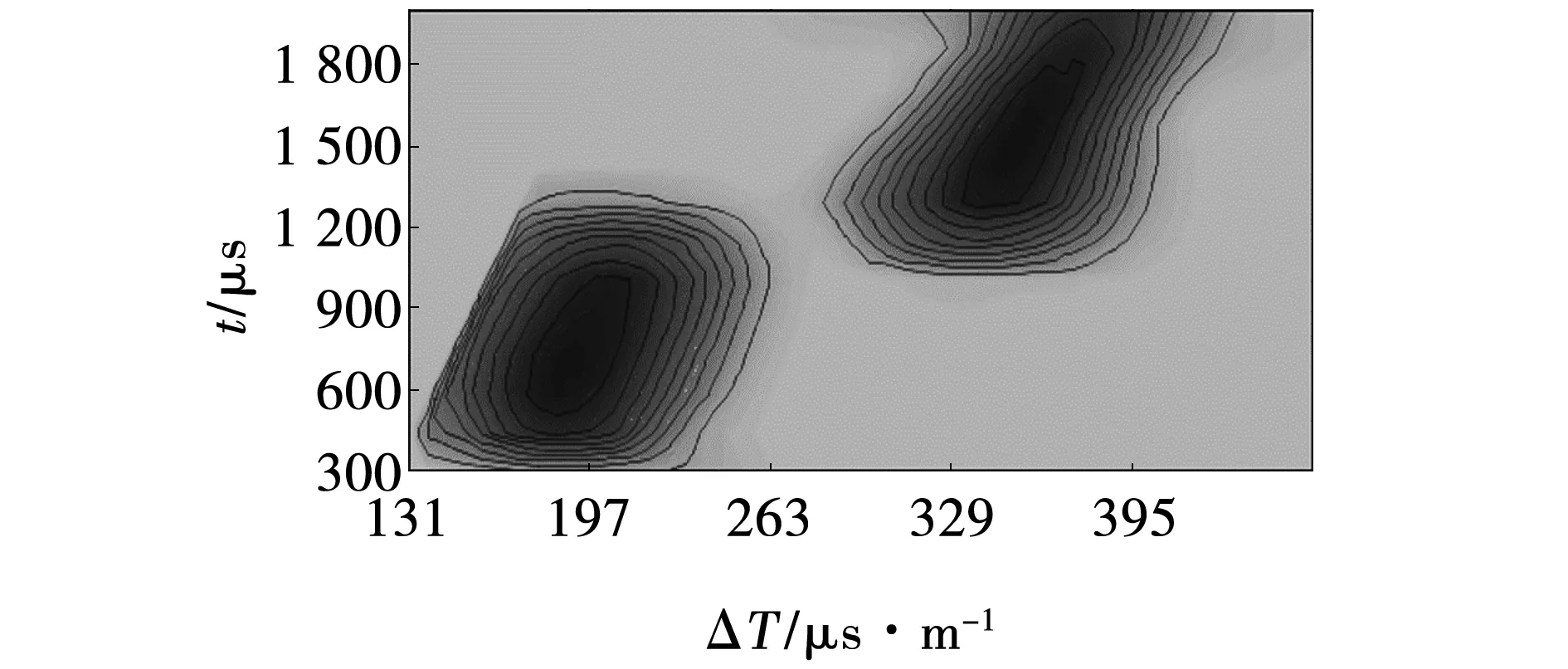
图2 函数关系Fig. 2 Function relationship

图2中,横坐标代表时差ΔT，纵坐标代表声波到时t。从图2中可以看出，纵波时差的大致分布范围为131～262 μs/m；横波时差的分布范围大致在295～427 μs/m之间。

3.2 数据分析

通过对阵列声波测井信息提取方法的研究和总结，采用改进后的奇异值分解方法借助CIFLog阵列声波处理模块对实际XMAC阵列声波数据进行处理。图3是玛湖油田玛十八井区某井在2 710至2 820 m井段模式波时差提取结果。从图3中可以看出，基于改进后的奇异值分解法所提取出的声波纵波时差DTC-New曲线与CIFLog软件STC方法提取出的纵波时差DTC曲线结果基本一致，没有出现大规模的曲线异常现象，且曲线间相关性较好。

该井数据各模式波形相关系数较高，根据DTC-New曲线可知，2 710～2 830 m深度段时差值稳定在187～243 μs/m之间，且曲线较为平滑，在2 719～2 732 m处以及2 811～2 818 m处时差曲线出现3～62 μs/m的波动，是由于地层岩性突变以及软地层造成的横波缺失所导致的结果，对纵波时差提取产生一定影响。在模式波时差曲线道横波时差曲线与偶极源横波曲线基本重合，总体上，根据实际测井情况可得出结论，基于改进后的奇异值分解法提取的阵列声波测井纵波时差结果较好，精度较高。

4 结束语

在阵列声波测井时差提取的方法基础上，对常规的奇异值分解法加以改进，通过子空间类算法和加权函数法，大大提高了声波时差的提取精度，应用子空间类奇异值分解法对玛湖油田玛十八井区某井XMAC测井数据进行解释处理。通过与STC方法时差提取结果对比分析可知，改进后的奇异值分解法提取出的时差结果更接近地层真实数据。该方法能够提取出可靠的声波时差，且计算效率较高，表明该方法在大多数地层中具有一定的实用价值，为进一步的阵列声波测井资料处理提供了新的思路与方法。