改进果蝇算法的运输车辆路径规划
2020-05-09胡浩然孙启智葛遵辉
赵 杰, 胡浩然, 孙启智, 葛遵辉
(黑龙江科技大学 电气与控制工程学院, 哈尔滨 150022)
0 引 言
物流配送车辆的路径规划是诸多规划出将物品运送到客户手中的最优方案,是一个多配送站的配送问题(Multi-depot vehicle routing problem,MDVRP)。目前,关于MDVRP问题有诸多的研究,Klapp等[1]以最小化总运送成本为目标,提出以车辆容量和行驶里程为约束条件的MDVRP,设计了禁忌搜索算法。Mirabi等[2]研究了以最小配送时间为目标的MDVRP,提出一种随机混合启发式算法。Kuo等[3]针对具有装载成本的MDVRP,设计了三阶段的变邻域搜索算法。Ran等[4]基于多承运商合作情形下的MDVRP,给出一种两阶段贪婪启发式算法。Salhi等[5]建立了异质车辆的MDVRP模型,根据车站是否共享、每种车辆数目限制、每个配送站的容量限制进行了扩展,配送车辆的行驶速度、行驶距离均会对燃料消耗量具有显著的影响,燃料消耗直接影响配送成本。Demir等[6]提出车辆装载量、发动机类型和尺寸、道路坡度等因素与配送车辆的燃料消耗具有一定的关系,影响配送成本。笔者提出考虑成本和燃料消耗优化MDVRP的方法,设计多种群果蝇算法对路径规划问题进行求解。
1 模型构建
1.1 燃料消耗量与成本模型
Sahin等[7]指出,载荷20 t的卡车满载行驶时平均每1 000 km的燃料消耗成本占据了物流总成本的60%。基于上述研究,构建了行驶里程与燃料消耗量的模型为
式中:ρ*——车辆满载时的燃料消耗率;
ρ0——车辆空载时的燃料消耗率;
mmax——车辆的最大装载量;
ρ(m1)——车辆装载量m1时单位行驶里程的燃料消耗量。
对于任意配送路径(i,j),当配送车辆配送完消费者i,驶向消费者j的这段路径中,设配送车辆k在该段路径上的实际装载量为mijk,则该段路径上单位行驶里程的燃料消耗为
ρij=ρ(mijk),
式中,ρij——车辆行驶在i和j之间的路径(i,j)上的燃料消耗率。
燃料消耗成本可以表示为
式中:Co——单位燃料成本;
dij——两个消费者之间的欧氏距离。
1.2 问题描述与模型构建
一个城市物流配送系统拥有M个配送中心,n个客户。每辆配送车辆的最大荷载量为mmax,考虑到车辆油耗和司机工作负荷存在约束,配送车辆的行驶距离不超过L。要求在满足车辆载重和行驶距离的约束条件下,合理安排配送车辆和车辆的行驶路线,基于最小化配送的成本和行驶距离,构建的模型为:
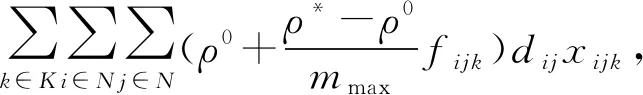
式中:Chc——每辆车的租赁成本费用;
Cvc——车辆单位行驶里程的变动成本;
Cfc——单位燃料消耗成本;
C——消费者位置的集合,C={v1,v2,…,vn};
n——消费者数量;
D——配送中心点集合,D={vn+1,vn+2,…,vn+M};
M——配送中心数量;
N——消费者和配送中心集合,N=C∪D;
K——可供使用的配送车辆集合,K={k1,k2,…,ks},
s——车辆总数;
dij——任意两点i和j之间的欧氏距离;
xijk——变量,若车辆k经过路径(i,j)值为1,否则为0。
为保证每个消费者仅被一辆车服务一次,加入的约束条件为:
为保证路径的连续性,加入的约束条件为:
车辆的容量约束和行驶时间限制分别表示为:
式中:mk——配送车辆k(k∈K)的最大装载量;
Ti——配送中心给消费者i的最晚收货时间;
mi——消费者i的需求量(0≤mi≤mmax,i∈C)。
车辆行驶过程中每段行驶路径上的载重量限制条件为:
mjxijk≤gijk≤(mmax-mi)xijk,∀(i,j)∈A,k∈K,
式中:gijk——配送车辆k经过路径(i,j)时货物的运输量;
A——路径集合,A={(i,j)|i,j∈N,i≠j}。
2 多种群的改进果蝇算法
VRP属于NP-Hard问题,国内外学者通常采用启发式或亚启发式算法进行求解[8-10],而文中模型涉及多个配送中心、燃料消耗量优化,使求解更加困难。Pan[11]受到果蝇觅食行为的启发提出果蝇优化算法(Fruit fly optimization,FFO)。FFO具有参数少,收敛速度快的优点,然而果蝇种群存在容易陷入局部最优的劣势[12],因此文中试图对其进行改进,在FFO的基础上,设计基于多种群的改进果蝇优化算法(Improved fruit fly optimization algorithm, IFFO)对文中模型进行求解。
2.1 解的编码
考虑到MDVRP属于典型的离散优化问题,文中采用自然数编码方式表示调度方案,设调度方案X=(x1,x2,…,xk)T,其中k表示车辆数目,xk=(0,r1,r2,…,rs,0)表示第k辆车的配送路线,0则表示配送站下标。在具体编码阶段,首先将MDVRP转化为多个VRP进行并行求解,然后根据油耗、成本等外部因素,为每一位客户分配配送车辆,设计配送车辆的行驶路线。具体解码过程:(1)根据果蝇个体编码,得到车辆的具体方位与排列顺序。(2)根据车辆的排列顺序,得到运输任务的序列T=(t1,t2,…,tk)。(3)将运输任务序列按照油耗配送时间等约束条件分配给W个运输车辆。(4)得到W个运输车辆根据建模条件的约束,自动划分每个车辆应到哪个目标点合理。(5)根据改进果蝇优化算法进行合理路径规划。
2.2 多种群方法
多种群的方法可以使算法在一次运行中获得多个较优解,已被广泛应用到车间调度等NP-Hard问题求解中[12]。针对果蝇算法求解过程中易陷入局部最优的劣势,文中采用多种群同时进化的策略,将果蝇种群中的个体分成多个子种群;同时,为了有效地利用各子种群中优势解的有利信息,加强子种群之间的交流协作,在果蝇算法的迭代过程中设计了子种群之间的交流互动策略,通过子种群中最优个体之间的信息交互,增强最优解的搜索效率和搜索精度。图1为子种群间的信息交互策略,在子种群1中随机选择一个果蝇个体,如选中子种群1中的个体d1作为父代1,然后分别以概率P0、P1和P2选择同一种群中的个体、其他子种群中的个体和全局最优个体执行交叉操作,这种子种群之间的信息交互方式提高了对问题最优解的搜索能力,同时以一定概率将种群中最优个体的优秀基因传递到当前个体中,可以实现快速收敛。
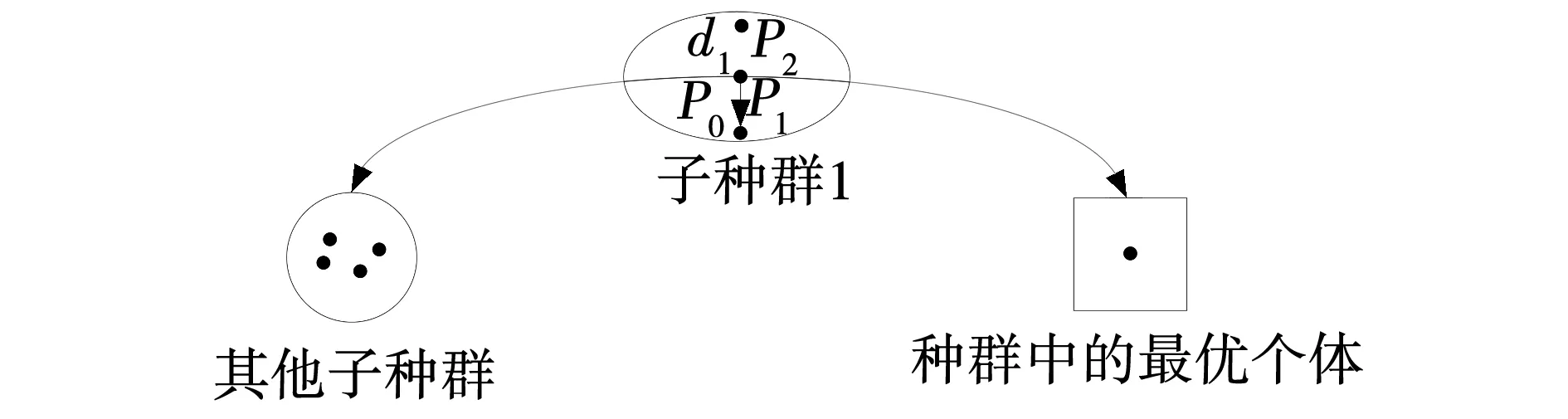
图1 子种群之间的信息交互形式Fig. 1 Information interaction between subpopulations
2.3 个体的遗传进化策略
在原果蝇算法中,果蝇个体的更新是通过不断的新旧最佳值比较而得到的,这样容易陷入早熟收敛境地,同时也会失去果蝇群体中果蝇的的个数,导致搜索速度下降,在文中设计的IFFO中,引入遗传算法中的交叉操作,以获得新的果蝇个体。为提高解的搜索能力,根据果蝇个体的编码方式设计了果蝇个体基因的删除、交叉策略,如图2所示。在同一种群中果蝇个体必有相似基因,但是在相似基因中所包含的信息不同。随机选中同一种群中的父代1果蝇个体和父代2果蝇个体,其中锁定父代1和父代2的相同基因,然后在父代1中删除一组相似基因,在父代2中删除另一组相似基因,由于父代1 中删除的基因与父代2中的基因存在相似基因,因此利用父代2中基因来代替父代1中删除的基因,进而实现了果蝇个体基因的删除、交叉策略。同理在父代2中删除的基因也是如此替代。此时产生新的果蝇个体,新的果蝇个体都具有了对方的基因信息,从而进一步提升搜素速度。
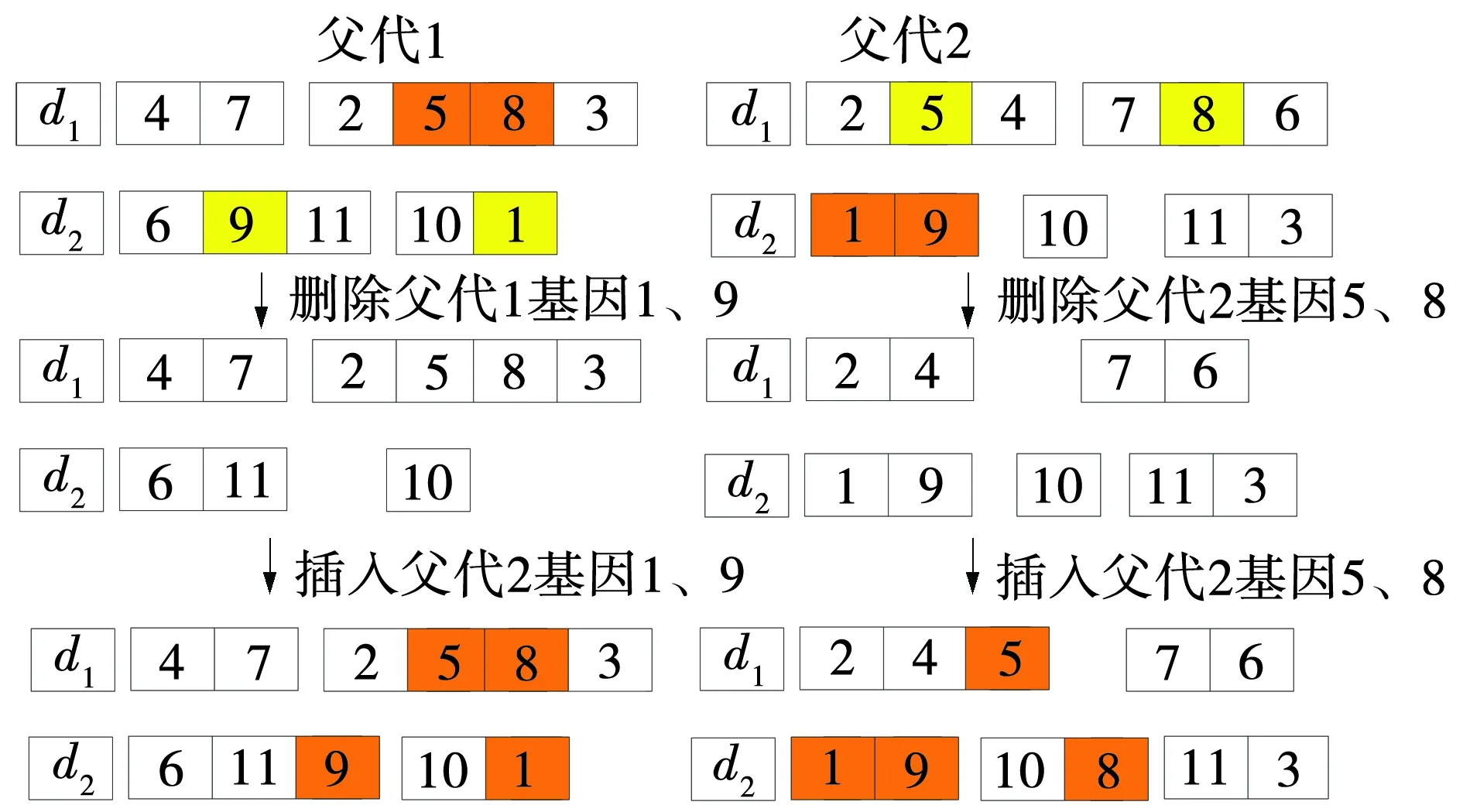
图2 交叉算子Fig. 2 Crossover operator
同时,为了提高果蝇个体间的多样性,在IFFO中采用交换(swap)、移位(insert)、倒置(invert)三种变异算子,三种变异算子的图示如图3所示。其中,交换变异是随机的选择两个不同位置,然后交换两个位置上的消费者;而移位变异是随机选择一个位置上的消费者,并将其插入到另一个随机位置,根据文中的编码方式可知,交换变异操作和移位变异操作选中的两个位置既可以是同一条子路径上的两个位置,也可以是不同子路径上的两个位置,这样就使得不同的路径能够顺畅的实现“信息交流”,增加解空间的搜索范围。倒置变异首先随机选中一条子路径(即一条配送路线),然后在该子路径上随机选择两个不同的位置,并将两个位置之间的消费者顺序进行翻转。
通过交叉和变异产生的新果蝇个体被放入到对应的种群中,并在选择阶段依据精英保留策略将该子问题的较好个体遗传到下一代。
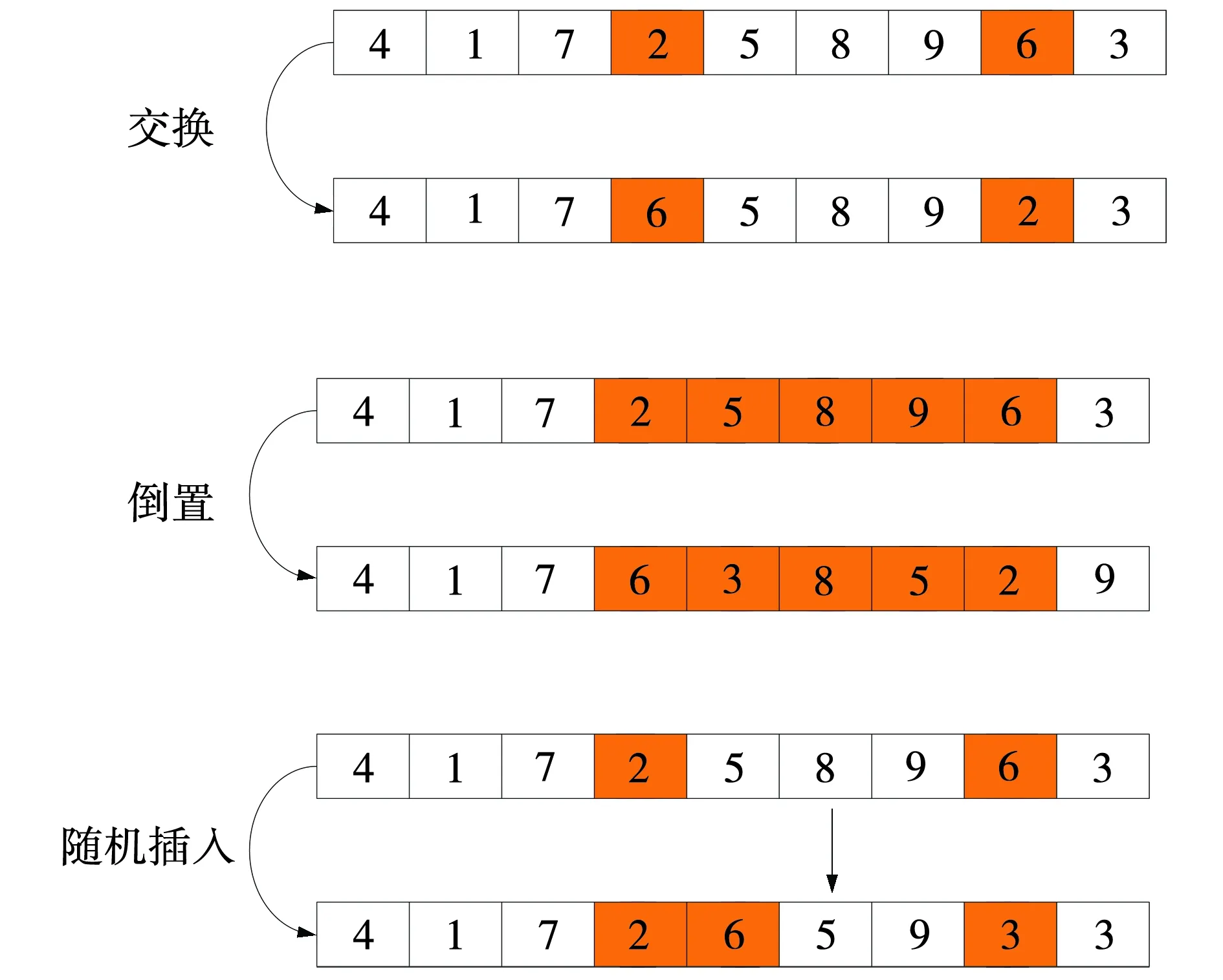
图3 交换、倒置、随机插入算子Fig. 3 Swap, invert, and random insert operators
2.4 算法步骤
初始化阶段主要分为两步:算法参数的初始化与种群个体的初始化。
Step1算法参数主要有:果蝇子种群个数(N)、子种群的果蝇个体数目(P)、算法迭代次数(M)、子种群交流互动准则(I)。
Step2为了扩大解的搜索范围,文中采用随机初始化的方式,具体来说,在为消费者i分配配送车辆时,随机选择一辆配送车辆,如选择配送车辆k1,将该消费者分配到该配送车辆,由配送车辆k1对其执行配送任务,当该配送车辆的容量和行驶路径超过最大限制约束时,再次随机选择另一车辆k2,直至所有的消费者均得到配送车辆对其执行配送任务后,种群个体的初始化阶段完成。
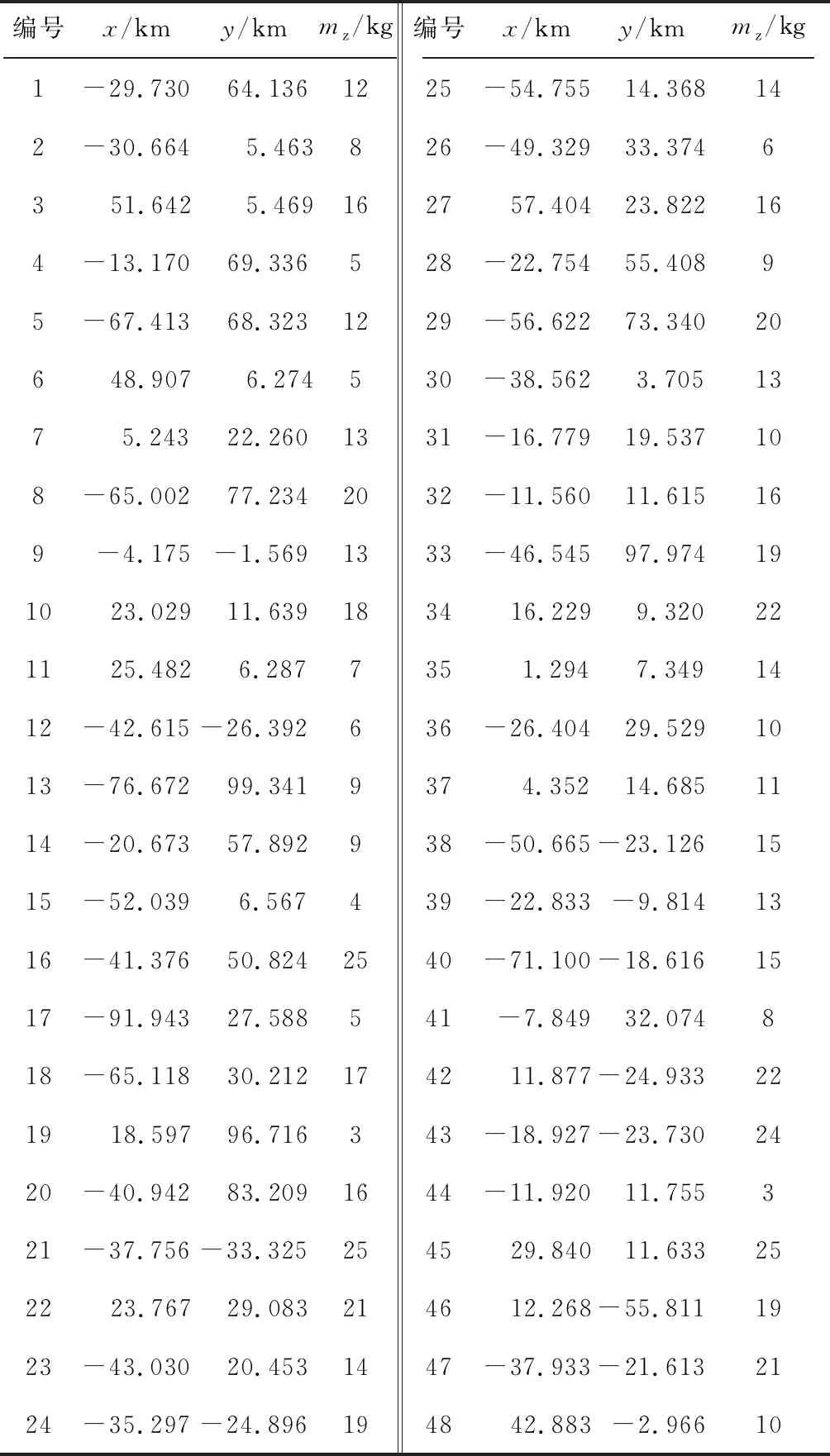
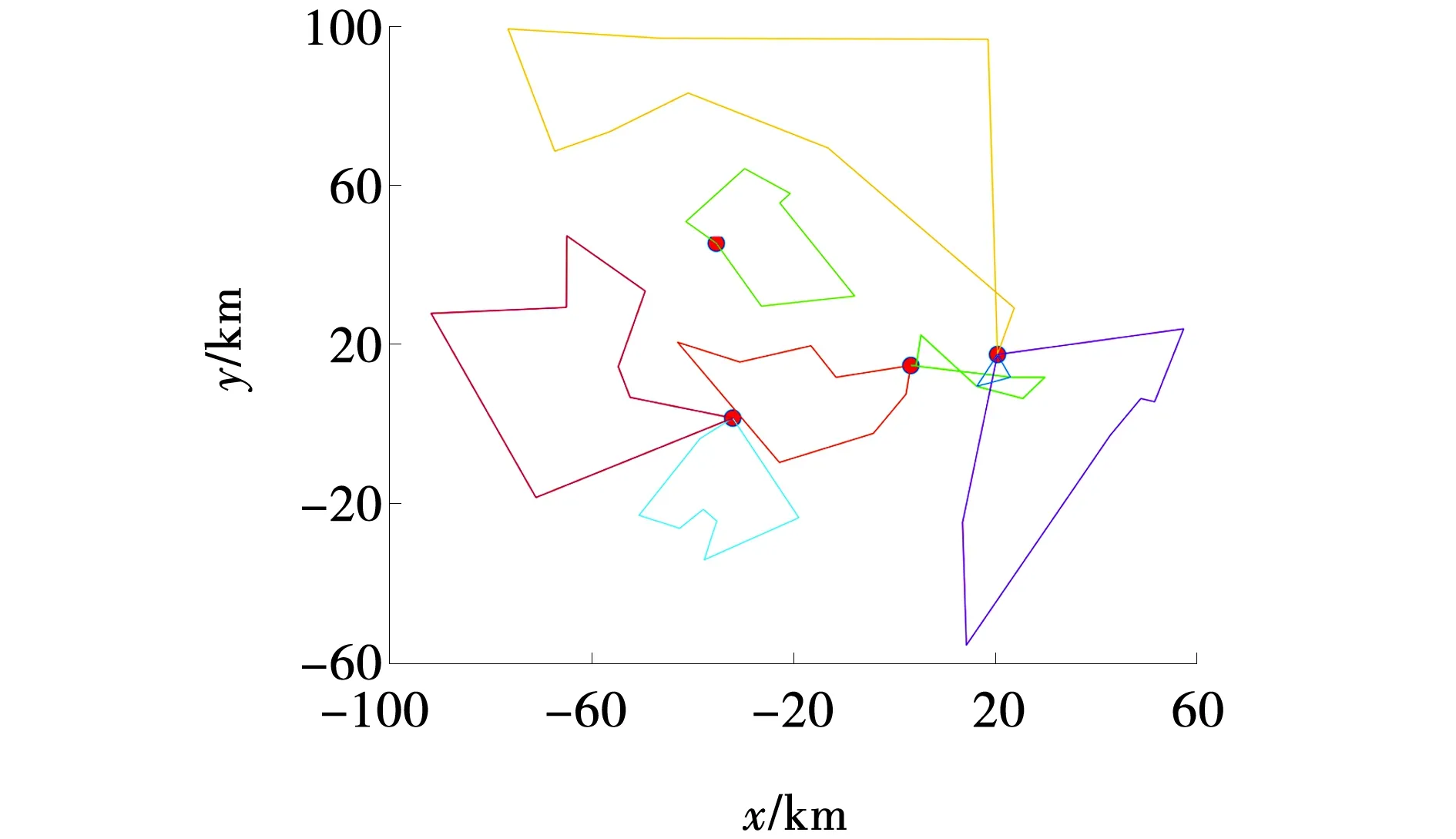
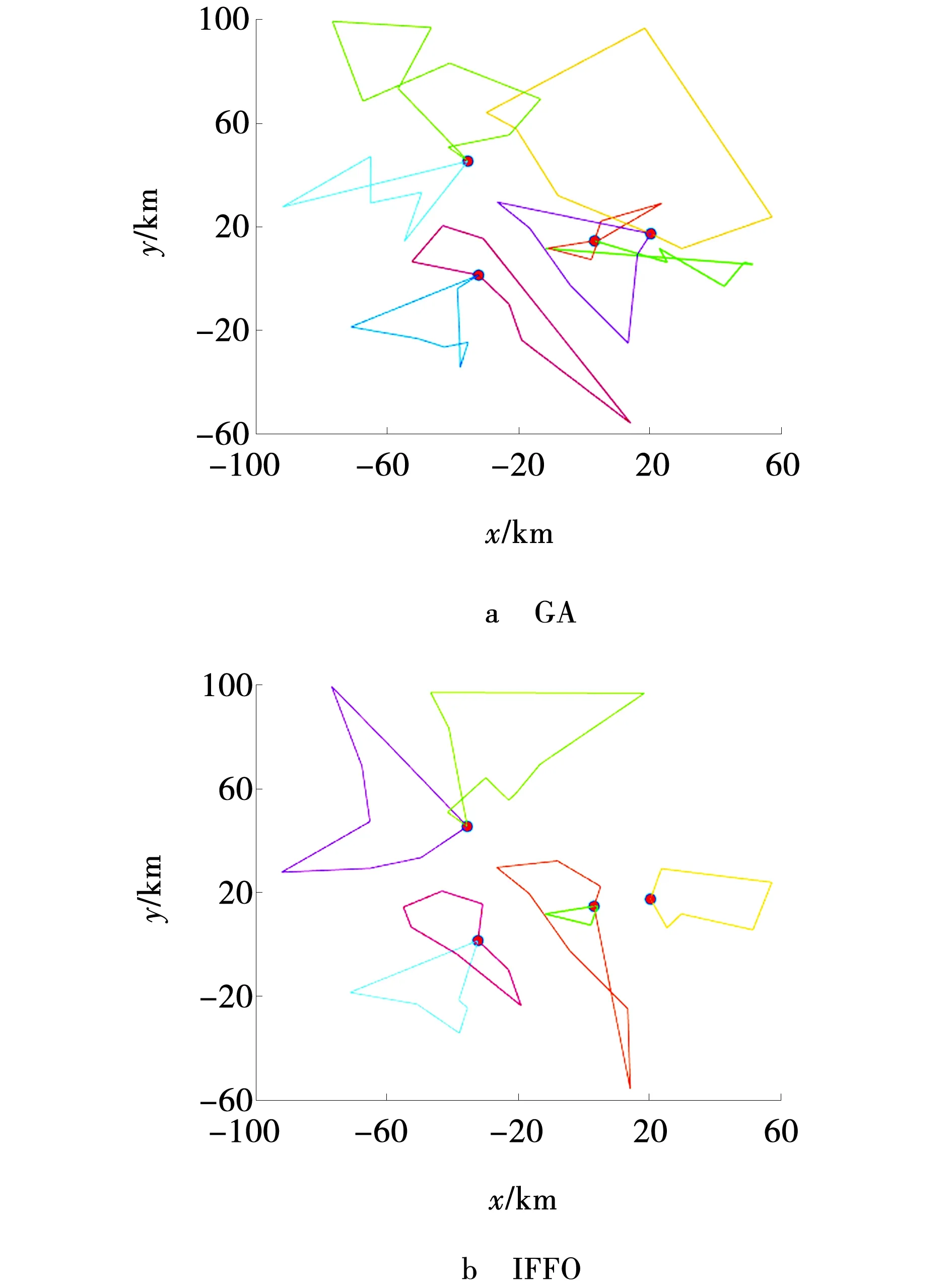
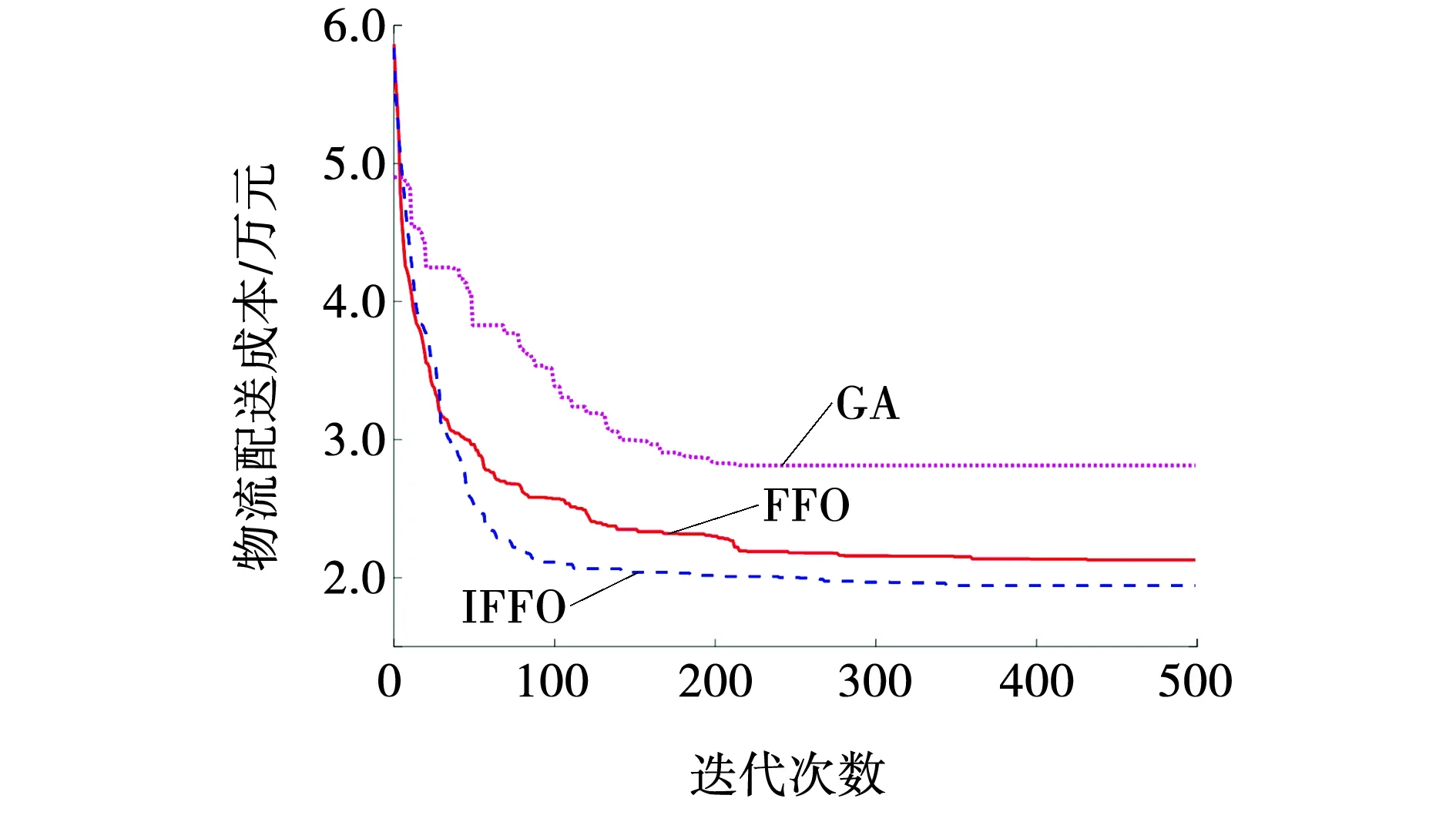
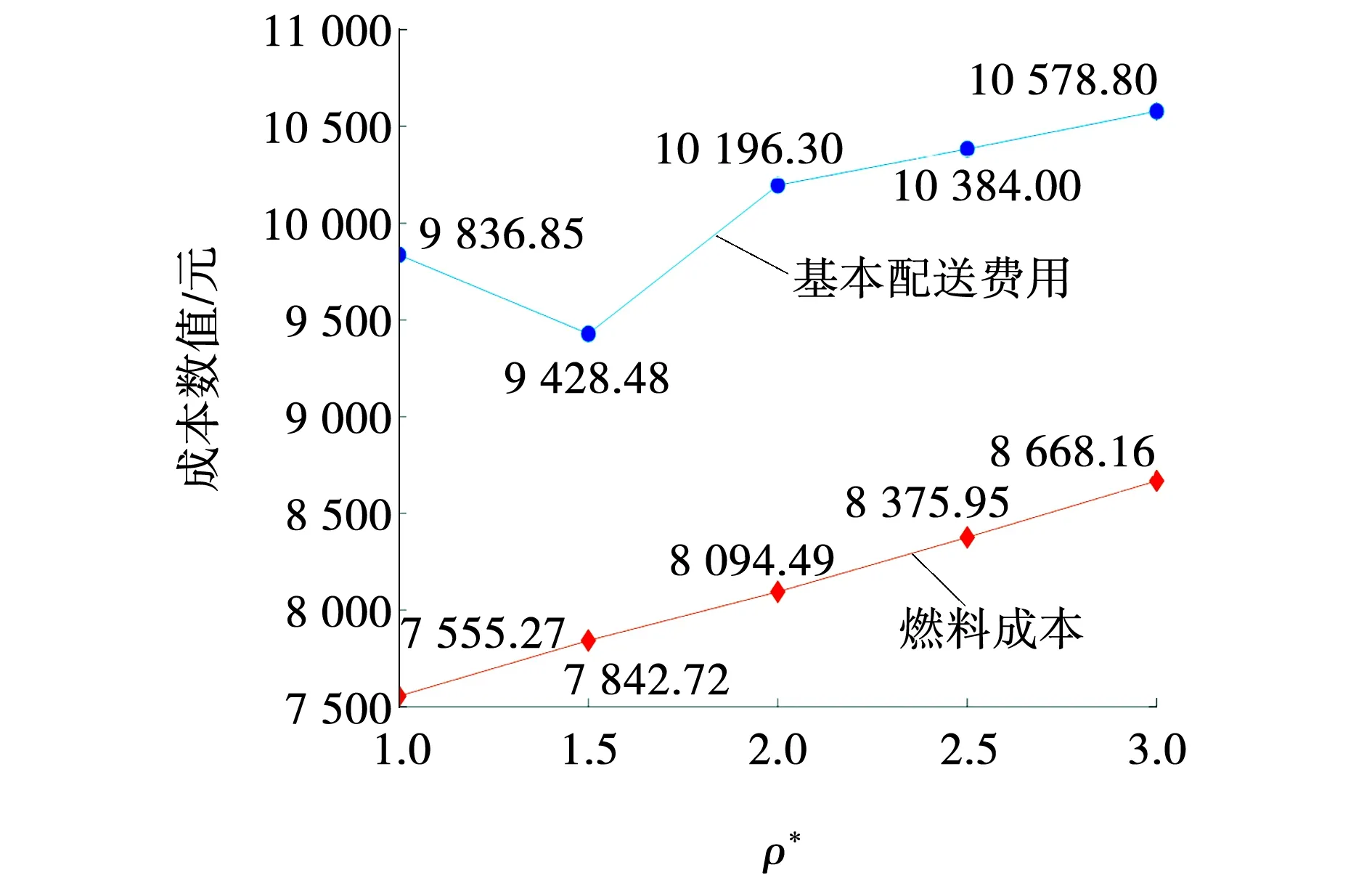
在嗅觉搜索阶段,对于每个子种群,在当前位置通过上述的遗传进化策略产生P个新的果蝇个体。如设子种群r在当前位置Xc处通过遗传进化策略新产生的P1个果蝇个体(X1,X2,…,XP)且新个体中的最优个体为Xb,那么在视觉搜索阶段执行果蝇个体的更新,如果目标函数值f(Xb) 对于基于种群的智能优化算法而言,种群中个体之间的交流协作可以扩展解的搜索空间,加快收敛速度,从而提高算法的求解效率和求解精度,而文中设计的多种群的果蝇算法具有多个子种群,且各子种群之间分别进行种群解的更新,缺乏种群之间的交流。因此,采用图1所示的子种群交流机制,在果蝇算法的迭代过程中,每经历P次的迭代次数后,执行多次种群之间的互动交流,以此为子种群选择性的引入外部种群或者最优个体的优良基因,进而提高对问题最优解的搜索能力。具体流程如图4所示。 图4 改进果蝇优化算法流程Fig. 4 Flow of improved fruit fly optimization algorithm 为验证模型及IFFO算法的有效性,文中以某电商物流公司为例进行数值仿真。该物流公司拥有4个配送中心,每辆配送车辆的最大载重量均为200 kg,每辆车的最大行驶距离均为500 km,每辆配送车的租赁成本为600元/辆,单位行驶里程的变动成本为5元/km;燃料费用为7.5元/L。4个配送站需要向48个消费者提供配送服务,用欧氏距离表示任意点之间的距离,已知各消费者的需求量,假设物流配送车辆从当天的上午10:00出发执行配送任务,并承诺在当天的17:00之前将货物送达,允许一定的延迟配送,但是最晚不能超过18:00,车辆的平均行驶速度为60 km/h。要求满足降低物流配送成本并减少顾客的延时收货时间,设计合理的调度和物流配送路线。其中配送站信息的坐标(单位:km)分别为:(4.163,13.559),(21.387,17.105),(-36.118,49.097)(-31.201,0.235),消费者信息如表1所示。 表1 消费者位置和需求量信息 遗传算法(Genetic algorithm, GA)在求解NP-Hard问题中具有快速收敛的求解优势,已成为求解车辆路径规划问题的重要方法。为了验证IFFO的有效性,将FFO、IFFO与GA三种算法求解结果进行比较,绘制了三种算法得到的配送路线图。其中,GA、FFO的种群数目设置为60,IFFO子种群数目设置为5,每个种群均有12个个体,GA的交叉率和变异率分别设置为0.9和0.1,IFFA每迭代10次进行一次子种群之间的信息交互,三个算法的总迭代次数均为500次。三个算法各独立运行20次,取最优计算结果如图5、6所示。 图5 FFO计算得到的配送路线Fig. 5 Distribution route obtained by FFO 图6 不同算法计算得到的配送路线 Fig. 6 Distribution routes calculated by different algorithms 由图5、6可以看出,GA和FFO运行后均得到了8条配送路线,而文中设计的多种群果蝇算法IFFO运行后得到了7条配送路线,即减少了一辆配送车的使用,也减少了配送路径的长度,这进一步说明了改进的果蝇算法可以规划出合理的物流配送路线。 为验证IFFO的实用性分别对FO、IFFO与GA三种算的收敛性进行对比如图7所示。 图7 三种算法的收敛性对比Fig. 7 Convergence comparison of three algorithms 从图7可以看出,在算法迭代的过程中,GA和FFO的求解结果和IFFO的求解结果差距不断增大,说明文中提出的多种群机制对于物流配送车辆的路径规划可扩大解的搜索范围,提高解的寻优速度和精度。 相比GA而言,GA计算得到的基本配送费用为13 000元,燃料成本为13 000元,超时赔付费用为2 000元。IFFO计算得到的基本配送费用为10 358元、燃料成本为9 789元、超时赔付费用1 622元,因此基本配送费用,燃料成本,超时赔付费用分别降低25.5%、32.8%、23.3%,相比基本的果蝇算法FFO计算得到的配送费用为11 228元,燃料成本费用为10 346元,因此IFFO计算得到的配送费用、燃料成本分别降低8.4%、5.1%。因此结合上述得到的配送路线、燃料成本、配送费用充分证明了改进的果蝇算法对车辆的物流配送有着很大的提升效率。 为了验证满载时的燃料消耗率参数ρ*对燃料消耗成本的影响,以ρ0=1不变,分别设置ρ*为间隔0.5的不同数值,探索ρ*不同取值下的物流配送成本变动情况如图8所示。 从图8可以看出,基本配送费用和燃料成本总体趋势均随着满载时的燃料消耗率ρ*的增加而增加,而当ρ*=1.5时基本配送费用得到了减少,这主要是因为在ρ*=1.5时,减少了一辆配送车辆的使用,使得基本配送费用减少了600元,从而降低了基本配送费用。 图8 基本配送费和燃料成本随ρ*的变化趋势Fig. 8 Trend of basic distribution fee fuel cost with ρ* 文中将配送车辆的行驶距离和载重量作为影响燃料消耗量的关键因素,建立了燃料消耗量模型和包含有多个配送站的终端配送路径规划模型,设计了问题的编码方式。在路径规划方面,考虑到传统果蝇算法易陷入局部最优的不足,设计了多个果蝇种群同时进化的多种群进化机制,给出了子种群个体之间的交流互动机制,应用遗传算法、果蝇算法和改进后的果蝇算法对模型进行求解,验证了改进多种群果蝇算法的有效性,确保了在燃料消耗,配送成本这些外部条件因素的限制下,规划出最合理的路径。改进的果蝇算法收敛速度得到明显的提升,扩大了搜索范围,提高解的寻优速度和精度。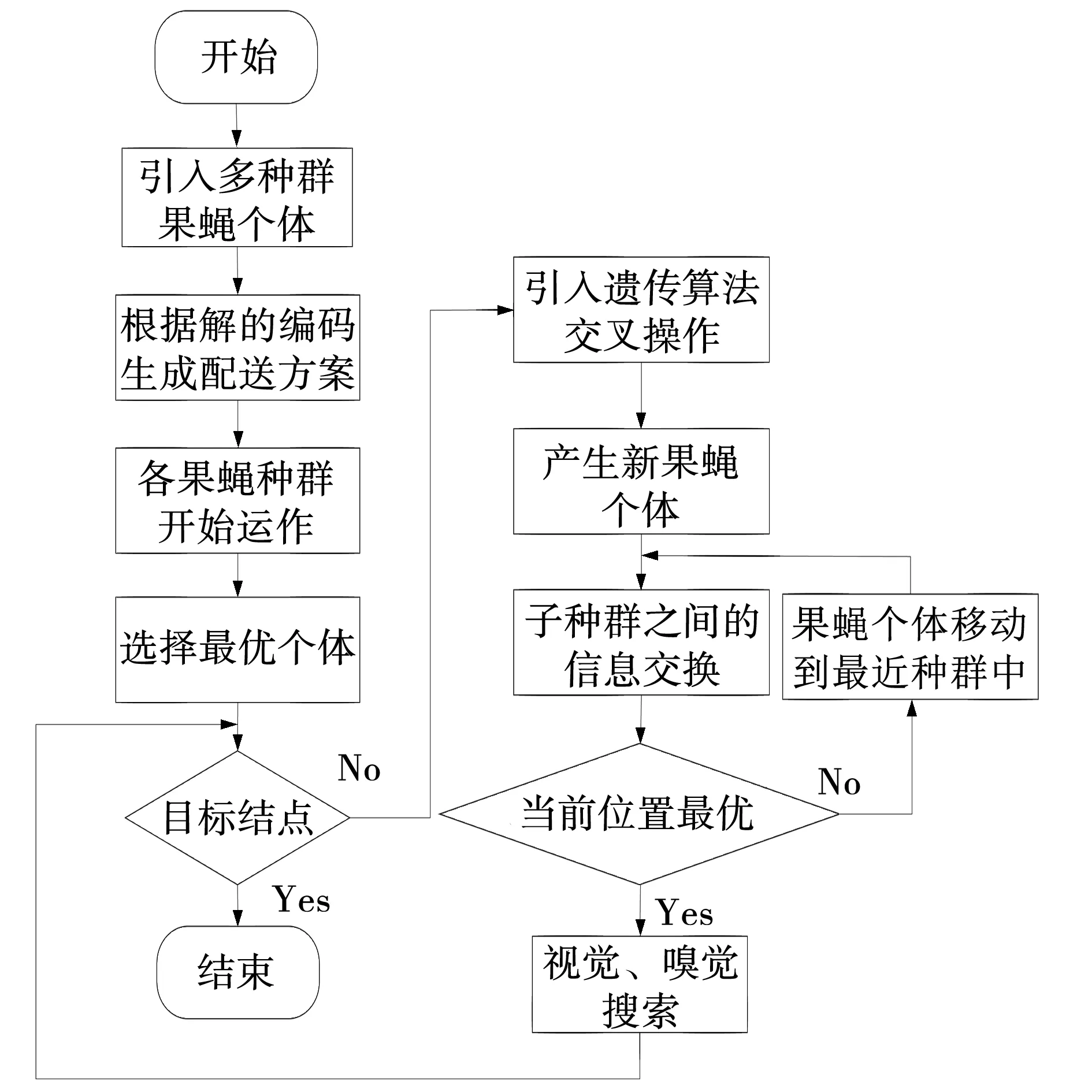
3 实例分析
3.1 IFFO算法求解效率
3.2 ρ*的灵敏度
4 结束语
