黏滞阻尼器对大跨度斜拉桥的减震效果优化研究

2020-05-09杨德健吴慧福

天津城建大学学报 2020年2期

杨德健，吴慧福，陈光

（天津城建大学土木工程学院，天津 300384）

我国是世界上地震多发的国家之一，地震造成的人员伤亡及财产损失不计其数，对斜拉桥的毁坏案例也是不胜枚举，给人们的正常生活带来极大威胁[1].国内外专家学者一直致力于研究如何减少地震带来的损失这一世界性难题.近年来，有关斜拉桥减隔震技术的研究受到了越来越多的关注.目前，针对桥梁有两种阻尼装置最适用，分别为与位移相关的金属不屈服约束支撑和液体黏滞阻尼器，其中黏滞阻尼器的应用最为广泛.Yamasaki等[2]研究了线性黏滞阻尼器的参数变化对斜拉桥塔底弯矩的影响；姜冲虎等[3-4]研究了在液体黏滞阻尼器和隔震支座的配合使用下桥墩的受力影响，均可得到黏滞阻尼器能有效减小地震响应.但上述研究的阻尼器安装位置主要是在桥塔处，与之对比的是传统的抗震体系，而对斜拉桥的其他位置的减震体系的研究以及减震体系之间的对比研究相对较少.

本文以某大跨度斜拉桥为主要研究对象，通过分析确定较为合理的参数，并对比分析4种工况下斜拉桥的位移和弯矩响应，确定最优的阻尼器安装位置，为今后同类型的斜拉桥的减震设计提供参考.

1 工程概况

以某混凝土斜拉桥为工程背景，跨径为152 m+370 m+152 m，桥面宽38.6 m.其主塔为H型，布置30对索，在索塔梁交接处布置一对0号索，同时在该部位布设有纵横向的限位装置.主梁采用C60混凝土，主塔高137.1 m，其中上塔柱、中塔柱高度分别为77.0，47.0 m，下塔柱高13.1 m，下塔柱倾斜布置，在塔底处向主梁倾斜.目标结构中的各杆件在Midas Civil软件中均采用梁单元模拟[5]，其有限元模型如图1所示.

图1 斜拉桥有限元模型

本工程所处位置为Ⅲ类场地，因是特大桥，考虑其安全性[6]，将地震设防烈度提高为8度，设计基本地震加速度值为0.2 g.因为强震记录的数量有限[7]，地震波采用拟合反应谱法进行模拟，生成适合于Ⅲ类场地的8度罕遇地震动加速度时程曲线，如图2所示，基于人工波时程曲线转化成拟合反应谱与目标反应谱对比，如图3所示.由图3可知：两者较为吻合，因此可用于抗震反应分析.计算中地震波沿纵向+竖向输入，且竖向地震动取0.65倍的水平地震动.

图2 人工地震波时程曲线

图3 人工地震波拟合反应谱与目标反应谱对比

2 黏滞阻尼器参数的确定

阻尼装置的耗能效率主要取决于阻尼系数和阻尼指数两个关键参数[8].一般情况下，大跨度斜拉桥选用的黏滞阻尼器的阻尼力与速度之间的关系为F=Cvξ，其中，F为阻尼力；C为阻尼系数，与构造尺寸有关；v为活塞与缸体的相对运动速度；ξ为阻尼指数，与介质黏度和孔径大小有关.阻尼系数和阻尼指数两个参数分别取[9]ξ=0.2～1.0，C=1 000～20 000 kN/（m/s）.

2.1 不同参数下的位移响应

为寻求相对最优的参数值，在模型的墩塔和主梁的交接处同时布置4组阻尼器，其中塔墩处每组4座装置，塔梁交接处每组2座阻尼装置，模型阻尼器的阻尼系数 C 分别为 1 000，2 000，5 000，8 000，10 000，20 000 kN/（m/s），阻尼指数ξ分别为0.3、0.4、0.6、0.8、1.0.将拟合的人工波输入到结构中，并进行地震响应分析，结构南侧主梁梁端、南侧塔顶、中间跨跨中（下文依次简称为梁端、塔顶、跨中）的位移响应曲线如图4所示.

由图4可知：当阻尼指数ξ一定时，结构梁端、塔顶、跨中的位移随着阻尼系数C的增大呈减小的变化趋势，且当C＜10 000 kN/（m/s）时，位移的衰减速率较大，即C的变动对结构位移响应影响很大；当C≥10 000 kN/（m/s）时，位移的变化速率较小，此时增大C对位移的影响可以忽略不计；当阻尼系数C一定时，结构的位移随着阻尼指数ξ的增大而减小；当阻尼器的C=10 000 kN/（m/s）、ξ=1.0时，结构的位移响应可以降到最低.

图4 位移随C、ξ的变化曲线

2.2 不同参数下的弯矩响应

不同参数不但对结构的位移响应有不同的影响，而且对结构的弯矩响应也有不同的影响.现重复2.1中操作，得到结构塔底、跨中、边跨的弯矩响应见图5.

分析图5可知：结构中塔底和跨中弯矩均可在ξ=1.0时取得最小值，此时边跨的弯矩响应也能得到有效控制；塔底和边跨弯矩都是随着C的增大而先减小后增大，当C=10 000 kN/（m/s）时结构的弯矩响应得到有效控制，此时结构跨中的弯矩响应同样能得到很好的控制.为了优化阻尼器的减震效果，延长结构的寿命，因此模型中阻尼器的参数选取C=10000 kN/（m/s），ξ=1.0.

图5 弯矩随C、ξ的变化曲线

3 减震体系地震响应分析

为了提高黏滞阻尼器对斜拉桥的减震效果，还需对阻尼器的安装位置进行研究.现调整阻尼器的放置位置，设置4种工况为：不加设阻尼器的结构（记为工况一），将阻尼器设置在墩顶处的结构（记为工况二），将阻尼器设置在塔梁交接处的结构（记为工况三），将阻尼器同时设置在“墩顶（工况二）+塔梁交接处（工况三）”的结构（记为工况四）.阻尼器数量恒定，每组4座.黏滞阻尼器的C、ξ按照最优参数设定，分别取C=10 000 kN/（m/s）、ξ=1.0.

3.1 不同工况的位移响应

现采用非线性时程分析法对上述4种工况进行地震响应分析，4种工况梁端、塔顶、跨中的位移响应如图6所示.

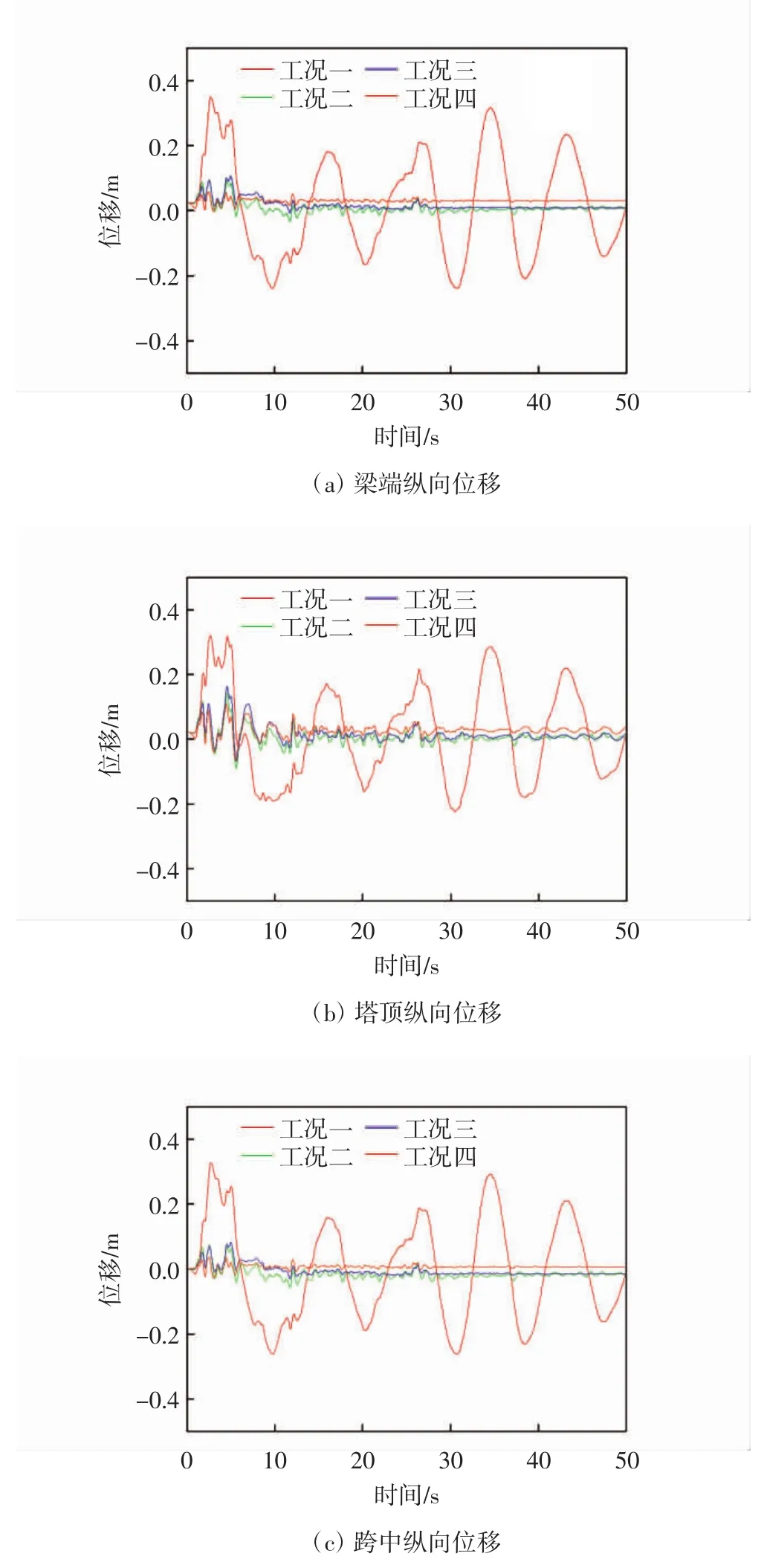
图6 4种工况的结构位移响应

为了更直观地比较梁端、塔顶、跨中位移响应的减小幅度，取结构的纵向位移响应峰值列于表1，不同工况下梁端、塔顶、跨中的纵向位移峰值如表1所示.

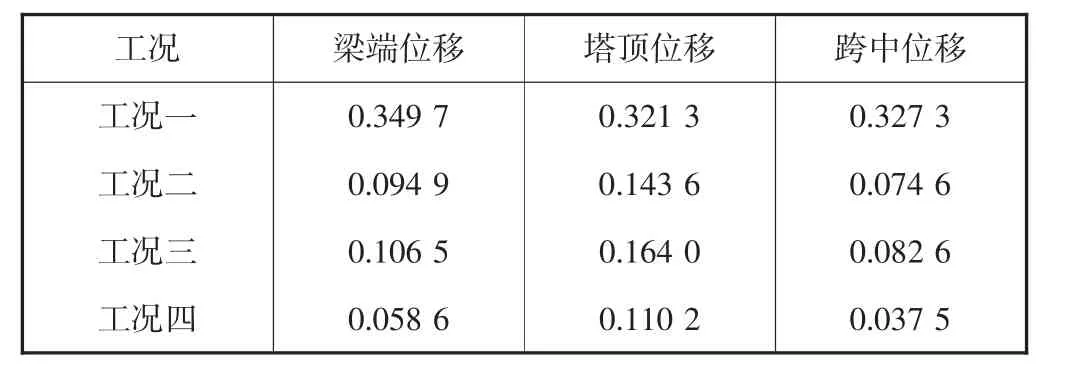
表1 不同工况下的纵向位移峰值 m

由图6a-6c可以看出：相比于工况一，加设阻尼器的工况中梁端、塔顶、跨中的位移响应均由原来的-0.4～0.4 m的变化区间减小，并稳定在-0.1～0.1 m的范围内，其中工况四梁端和跨中处的位移响应均是在6 s时开始趋于稳定，用时最短；工况二、工况三在短暂的波动之后也随之趋于稳定，并且其位移减小率差别很小，而且两者都略小于工况四的.结构在设置阻尼器后，主梁梁端的纵向位移大为减小，其中工况四的纵向位移减小得最多；结构主塔塔顶处的位移响应在地震波输入12 s以后才开始趋于稳定，其中也是工况四的位移响应减小最多；结构跨中纵向位移响应与梁端纵向位移响应的变化趋势相似.由此可知，设置阻尼装置可以有效防止主梁因位移过大而造成的梁端与桥台结合处脱离，进而使限位装置被频繁碰撞而造成剪切破坏.在结构的纵向设置阻尼器，可以有效减小该方向上的位移动力响应.

通过表1可知：工况二、三、四中各点位移峰值均小于工况一，其中跨中位移的减小幅度最大，减小幅度分别为77.20%、74.76%、88.54%；对于不同工况，在同一位置处的纵向位移，工况四的效果最明显，位移峰值减小最多，其次是工况二的，工况三减小得最少.

3.2 不同工况的弯矩响应

为了更全面分析结构在设置阻尼器后的地震响应的变化，输入地震波后，斜拉桥的塔底、边跨和跨中弯矩响应如图7所示，其弯矩响应峰值如表2所示.

分析图7a-7c可知：工况二、三、四相对于工况一，在地震动时程作用的初始阶段，弯矩响应与原结构一样有所增大，但随着时间的增加，弯矩变化幅度越来越趋于平稳，而且弯矩有大幅减小；其中，工况四相对于工况二、三弯矩响应减小的幅度更大，弯矩响应的变化趋势最为稳定.

由表2可知：工况四的弯矩最大响应有较大的减小，塔底、边跨、跨中弯矩最大响应分别减小了30.79%、13.58%、2.23%；工况三的塔底弯矩峰值大于工况一的，显然工况三对塔底的弯矩控制不利；塔底、边跨和跨中的三处弯矩工况二与工况四相对于工况一的弯矩峰值均有所减小，但工况四比工况二减小得更多.

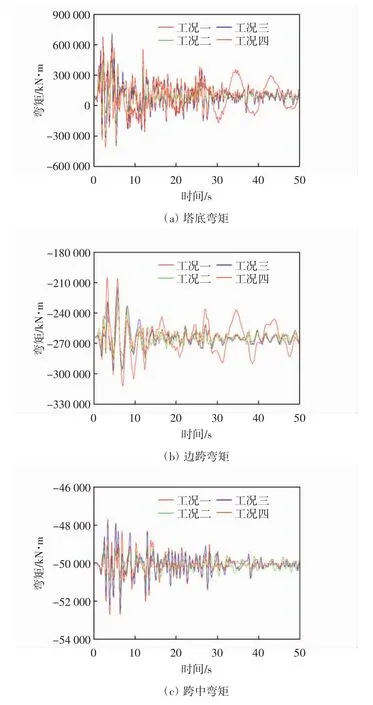
图7 4种工况的结构弯矩响应

表2 不同工况下的弯矩峰值 kN·m

对于大跨度斜拉桥，在不同位置安装阻尼器，综合考虑位移响应和弯矩响应，虽然工况二、三、四相对于工况一的位移响应均有所减小，但如果采用工况三则对塔底的弯矩控制不利；工况四的最大弯矩响应比工况二减小得多，工况四不仅能有效减小结构的位移响应，而且还能有效控制结构的弯矩响应.因此，综合考虑结构在地震作用下的整体变形及弯矩响应，工况四是大跨度斜拉桥抗震设计的较优选择.