基于速度前瞻的数控运动轨迹控制及平滑处理

林 浒，刘 飞

1(中国科学院大学，北京 100049)2(中国科学院 沈阳计算技术研究所，沈阳 110168)3(中国航发沈阳黎明航空发动机有限责任公司，沈阳 110043)

1 引 言

高速数控加工是提高零件加工质量和效率的重要手段，超快激光加工尤其如此[1]，超快激光加工质量的关键取决于加工轨迹在拐角处的质量优劣.因此，拐角处的加工速度是高速加工需要着重考虑的问题之一.关于拐角平滑处理的研究，目前的研究大多朝着两个方向进行研究，一是基于前瞻的速度规划算法的研究，通过避免不必要拐角处的加减速改善加工效果，此外，通过在拐角处增加过渡元素来解决，关于过渡元素的选取问题，很多专家学者进行了大量的研究，文献[2]采用样条曲线作为过渡元素进行研究，但由于样条曲线插补运算量较大，灵活性不足，其推广应用还有待于深入研究；文献[3,4]采用三次多项式样条作为过渡元素进行研究，但由于该样条曲线插补对于空间曲线的过渡转接运算量较大，使用范围仍然受到很大的限制，为此，提出一种既计算简便并且满足灵活性要求的过渡元素是非常必要的.

由于圆弧插补技术较为成熟[5]，并且运算效率高，本文采用空间圆弧实现程序段间的轨迹转接，保证轨迹的C1连续性，其具有计算简单、技术成熟等特点，使用空间圆弧可以简洁地描述数控运动轨迹在拐角处的平滑过渡曲线，此外，采用实时前瞻技术，实现平滑且高速的轨迹运动效果，提高工件的整体加工效率[6]，有利于加工轨迹计算的实时性的提高，根据目前数控系统中常用的编程元素，其中包括直线运动段及圆弧运动段，本文分别针对不同的连接情况进行具体研究，并进行了实际的加工验证.

2 轨迹平滑处理的基本思想

在数控加工系统中，运动段拐角的处理是提高运动轨迹平滑的关键问题[7,8]，主要原因包括如下两方面：其一，拐角速度的确定，如果拐角处理处理不当，易造成加工过程中频繁的加减速，显著降低运动的平滑性；其二，提高拐角处轨迹的平滑性，在保证轨迹误差的情况下，在拐角处添加具有平滑特点的运动段，满足较好的轨迹平滑性.为了解决以上问题，本课题开展了运动段拐角处过渡技术的研究，其基本思想见图1所示，在满足轨迹误差的前提下，在拐角处添加圆弧、样条曲线等过渡运动段，保证加工轨迹的平滑性，在此基础上，通过采用实时前瞻技术，在满足运动拐角处加工精度及机床加速性能的前提下，最大程度的提高拐角处的运动速度，从而提高工件的整体加工效率，并实现平滑的轨迹运动效果.

3 轨迹平滑处理技术

高速加工过程中，要求数控系统确保机床运动的平稳性，防止较大的冲击载荷影响零件的加工质量，并保护机床的进给系统，高速加工同时也给数控系统带来一定的挑战[9]，若在加工区域中存在尖锐的拐角或是高曲率路径时，由于高速加工的进给速度都比较高，很容易产生过切、拐角处表面质量不好等情况，因此需要在加工轨迹拐角处进行速度的平滑处理，以下分别针对编程轨迹间不同的连接情况进行分析.

3.1 直线与直线间拐角过渡

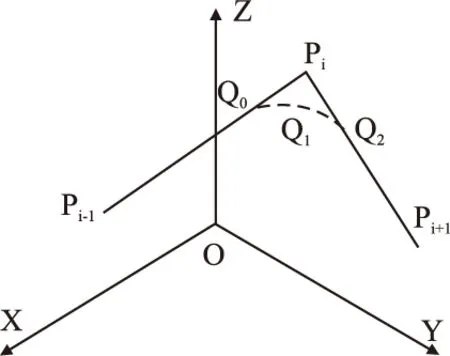
图2 圆弧过渡示意图Fig.2 Circle transition diagram

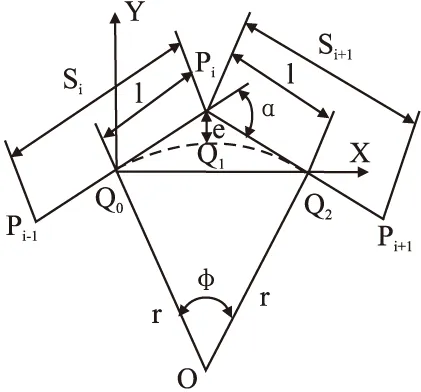
图3 圆弧过渡坐标系Fig.3 Arc transition coordinate system

图3中，ΔQ0OQ2根据平面几何知识，易知为等腰三角形，根据切线的基本性质可以得出ΔQ0PiQ2也为等腰三角形，因此两运动段的拐角点Pi与过渡圆弧的起始点Q0和结束点Q2之间是等距的，此处定义以上距离为过渡距离，即Pi到起始点Q0和结束点Q2的距离，该距离为两运动段Pi-1Pi和PiPi+1完成圆弧过渡所需的最短距离.此处定义轮廓误差为两运动段的拐角点Pi与过渡圆弧间的最短距离，该距离可以由图中线段PiQ1的长度表示，由于PiQ1垂直于过渡圆弧上过点Q1的切线，由几何关系可知，由PiQ1表示的轮廓误差即为拐角点Pi与过渡圆弧间的最短距离.

(1)

通过关系公式(1)可进一步推导，根据相邻运动段之间的夹角α、加工精度所确定的轮廓误差，得出两运动段间的过渡距离l、过渡圆弧的半径r各自与α及e的关系为公式(2):

(2)

采用过渡圆弧实现相邻运动段间的平滑过渡时，存在着实际路径与原始路径间的拟合误差.首先，考虑运动段拟合后满足轮廓误差的要求，根据轮廓误差、两运动段间夹角和运动段长度的几何关系，确定过渡圆弧的半径以及过渡圆弧的起始点和结束点，其次，需要考虑过渡圆弧上的进给速度需满足机床的最大加速性能，由最大加速度确定过渡圆弧的最大进给速度.

1)确定过渡圆弧半径、起始点及结束点

在两运动段间添加过渡圆弧后，原直线运动段与直线运动段的连接以直线-圆弧-直线的连接代替，实际加工路径与原始路径间存在着拟合误差，该误差即为轮廓误差.为了满足轮廓加工精度的要求，在确定过渡圆弧的半径和起始点、结束点时首先需满足轮廓误差的要求，因此需要将最大轮廓误差Em作为约束条件确定过渡圆弧的其他参数.将Em代入公式(3)中，可以得到满足最大轮廓误差的过渡距离lc为：

(3)

由于公式(3)是根据图3的几何关系得到，对于通常情况下得运动段，Em远远小于运动段的长度，因此Em约束下的过渡距离lc必定小于相邻运动段的长度.

2)过渡圆弧段最大进给速度的确定

为保证加工过渡圆弧时满足机床的加速度性能，考虑到过渡圆弧加工时，方向的不断变化所引起的向心加速度，根据运动学原理，向心加速度与过渡圆弧的进给速度有关，因此，确定过渡圆弧进给速度时要考虑向心加速度的约束.由向心加速度公式，最大进给速度vm与机床的最大加速度为am、过渡圆弧的半径r的约束关系为公式(4):

(4)

因此，为保证过渡圆弧加工时，既满足加工精度的要求又满足机床的加减速性能，进行过渡圆弧段加工的最大速度应选择工件程序设定的最大加工速度与机床最大加速度约束的速度vm中的较小值，即：

v=min(F,vm)

(5)

为满足过渡圆弧段加工时的进给速度，在进行过渡圆弧段之前，基于前瞻算法进行进给速度的规划，使过渡圆弧的起始点的进给速度为v，并保证过渡圆弧的加工过程中速度保持不变.

3.2 圆弧与直线间拐角过渡

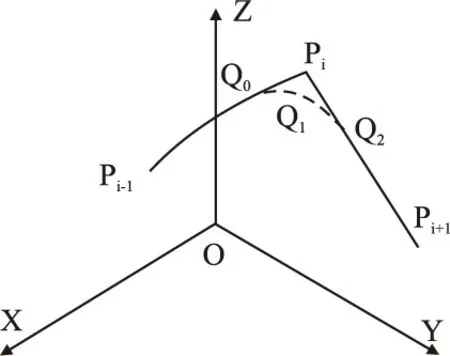
图4 圆弧与直线过渡示意图Fig.4 Diagram of transition between arc and straight line

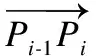
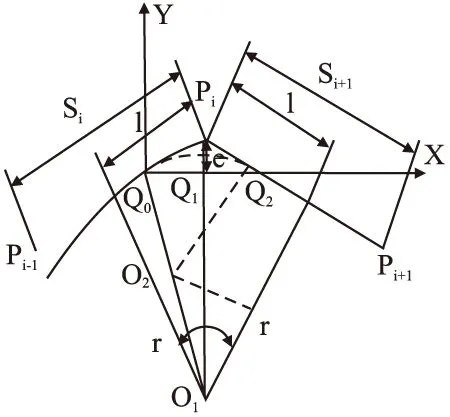
图5 圆弧与直线过渡坐标系Fig.5 Transition coordinate system of arc and straight line

假定过渡圆弧的圆心角为φ，过渡圆弧与原轨迹间的误差为e，Pi与O1间的距离为h，Pi与切点间的长度为d，则:

(6)

考虑到运动段自身长度限制，且每条线段上的过渡距离不超过自身长度的一半，则有:

(7)

并确定修整后的半径：

R1=ls·tanθ

且过渡圆弧的加工需要满足法向加速度要求，设满足要求的半径为R2， 符合工艺要求的加工速度为v，法向加速度为an，则:

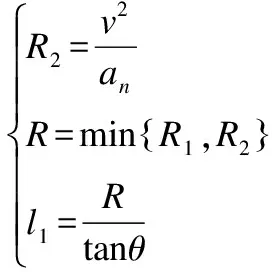
(8)

此外，圆弧与圆弧连接的处理方法与圆弧与直线拐角过渡类似，在此不再详述.

3.3 过渡圆弧段最大进给速度的确定

在加工过程中，需要确定以下几个速度量：Vnormal、Vplanar、Vgoal、Vmaz_alt、Vplan，Vreq等.其中Vnormal为满足最大法向加速度要求的最大速度约束；Vplanar计算平面合成速度的约束；Vgoal为程序段终点的速度；Vmaz_alt为满足拐角要求的最大速度约束；Vplan为规划过渡圆弧所采用的速度；Vreq为运动段的速度命令值.各速度确定的流程如下：

1)在包含圆弧与直线的平面上，确定最大合成速度Vplanar.

2)计算法向最大加速度及由最大法向加速度所确定的最大速度Vnormal.

3)根据相邻运动段的命令速度及修调倍率，确定拐角处的目标速度Vgoal.

4)在包含圆弧与直线的平面上，确定满足拐角要求的最大速度Vmax_alt.

5)计算满足以上约束的目标速度Vgoal、规划速度Vplan.

4 实验与结果分析

根据以上控制系统的设计方案，利用自主开发了超快激光控制系统，其中，工控机选用贝加莱第三代嵌入式工控机Autumation PC910，采用沈阳高精数控智能技术有限公司自主研发的GJ430数控系统，激光加工设备，包括激光器、扫描系统、加工检测设备、加工监测设备等，由中科院西安光学精密机械研究所提供.在该机床上对航空工件的异性槽，如簸箕槽，其加工形貌如图6所示，经测试后，轨迹拐角处的加工精度满足设计要求.

图6 簸箕槽加工形貌Fig.6 Machining appearance of dustpan trough

5 结 语

拐角速度处理是制约高速加工的瓶颈问题之一.为了优化工件拐角处的加工效果，本章从轨迹平滑、提高拐角速度等两个方面为切入点进行研究，从而实现超快激光数控机床的高速加工性能，在轨迹平滑方面，本文采用空间圆弧实现程序段间的轨迹转接，保证轨迹的C1连续性，其具有计算简单、技术成熟等特点，此外，在提高拐角速度方面，采用实时前瞻技术，实现平滑且高速的轨迹运动效果，提高了工件的整体加工效率.