一种半监督机器学习的EM算法改进方法

夏筱筠，张笑东，2，王 帅，2，罗金鸣，崔露露，2，赵智阳，2

1(中国科学院 沈阳计算技术研究所，沈阳 110168)2(中国科学院大学，北京 100049)3(沈阳工程学院，沈阳 110136)

1 引 言

期望最大化(Expectation Maximization，EM)算法是一种被广泛应用于极大似然估计的迭代计算方法，用于处理大规模数据不完整问题.

EM算法实际上是一种基于梯度上升的方法，在应用于模型参数估计时能够保证迭代之后的似然函数是递增的，因此有一个很大的弊端就是通常只能得到一个局部最优解.对于EM算法，国内外学者提出了很多改进方式，比较经典且应用比较广泛的有PX-EM算法、ECME算法、MCEM算法.PX-EM算法利用协方差对M步的计算进行修正，通过获取数据的额外信息达到加快收敛速度的目标，在应用上更加简化，而且未破坏EM算法单调收敛性质.但PX-EM算法那也有其缺点，在扩充参数模型上很难找到一个通用的标准，所以它在局部最优解问题上并没有得到很好的优化[1]；ECME算法对E步进行了简化处理，由于它在极大化过程中针对的一直是实际对象，而不是实际对象的附近量，其拥有的收敛速度比EM和PX-EM算法都要大.然而，ECME算法在局部收敛的问题上依然没有给出有效的处理方法，依然延续了EM算法所固有的性质[2]；MCEM算法用蒙特卡罗的方法对EM算法进行优化，对EM算法中的期望显示表示进行了改善，从而加速了收敛速度，但由于这种方法过于灵活，在模拟容量选择和收敛性准则的确认上很难，而且失去了EM算法的单调性，难以对其收敛特性进行估计，依然在局部最优问题上没有给出有效解决方案[3].

综上所述，EM算法及其改进算法存在在局部最优化问题上还存在着很大的不足，国内外学者在改进方法上侧重于解决其收敛速度问题，针对EM算法进入局部最优问题还未提出有效方法.对此，本文将半监督机器学习方法用于EM算法改进，首先在最大似然函数中加入最小二乘惩罚项，引入非负约束作为先验信息，然后结合半监督机器学习法，将EM算法改进方法转化为处理最小化的问题，再采用最大似然算法求解EM问题，有效地求解了混合矩阵和高斯混合模型参数，实现EM算法的改进.通过实验理论与实验结果分析表明改进后EM算法不会陷入局部最优，得到的结果更加可靠.

2 基于半监督机器学习的EM算法改进分析

2.1 改进EM算法先验信息的获取

以先验理论为基础依据概率惩罚定理以及二项分布概率函数[4]，将最大似然函数表示为：

(1)

公式(1)中，αji=αj(xi)=P(y=j|xi)，yji是j×1的某一个一维向量，代表第i个观测变量，xi=(x1,x2,…,xp)用于描述协变量.

通过计算，L对数似然函数课表示成：

(2)

对公式(2)关于j×p进行一阶偏导求解，那么得分函数表示为：

(3)

对S(β)=0进行求解，从而获取参数估计值β.

将惩罚项添加到最大似然函数中会大大减小得分函数所带来的误差[5]，本文添加的惩罚项为最小二乘惩罚项，公式为：

(4)

公式(4)中，p=[p1,p2,…,pi]T代表估计向量；f=[f1,f2,…,fj]T代表惩罚向量；Q(f)为惩罚项；χ代表对惩罚项的影响程度，χ值可利用实验获取；H为i×j系统概率矩阵；k代表迭代次数.

利用最优化法对上述惩罚项进行求解，并且通过OSL算法获取迭代公式：

(5)

需要指出，Q(f)主要包含二次与非二次，二次惩罚项结构简单，通常会导致数据丢失，而非二次惩罚项可避免该弊端[6，7]，本文选用非二次惩罚项.

(6)

式中，M=Med(fzj,j′∈Nzj)，Nzj代表fzj的邻域.

将非二次惩罚因子加到最大似然函数中后，那么含有多个参数的估计误差为：

(7)

事实上，就是在似然函数添加惩罚最小二乘项|Q(β)|0.5，似然函数可描述成：

L(β)*=L(β)|Q(β)|0.5

(8)

对数似然函数可描述成：

l(βj)*=S(β)0.5log|Q(β)|

(9)

得分函数的基本形式可描述成：

S(βj)*=S(β)-Ab(β)/n

(10)

其中，

b(β)/n=(XTWX)-1XTWε

(11)

A=XTWX

(12)

利用得分函数与添加惩罚项之后的最大似然函数，得到先验信息如下：

S(β)*=S(β)-XTWε

(13)

2.2 EM算法改进的实现

在上述处理最大似然函数的基础上，本节首先对EM算法实现过程进行分析，然后引入非负约束先验信息，采用半监督机器学习的方式对EM算法实现改进.

EM算法指的是观测数据是否含隐含变量条件下，也就是所用观测数据是非完整数据的情况下，使用极大似然函数对这些数据进行处理，经过多次循环，最终获得最优值的算法[9，10].

在传统EM算法中，通常会使用最大似然准则完成对参数估量.假设存在N个数据X=[x1,x2,…,xN]，这些数据是通过特定分布p(X|θ)独立采样获取[11]，结合先验知识，则似然函数可描述成：

(14)

最大似然准则为找到符合以下条件的模型参数：

θ*=arg maxL(θ|X)

(15)

为了简化计算过程，使用函数log(L(θ|X))进行最终解的优化，其中，log(L(θ|X))为对数似然.如果Z代表一个数据集，其中有两组数据，一组是已观测数据，另一组是未观测数据，用X代表已观测，用Y代表未观测，则Z=(X,Y)一般被称作完全数据集与缺失数据集，则有：

p(z|θ)=P(x,y|θ)=p(y|x,θ)p(x|θ)

(16)

假定似然函数可表示成：

L(θ|Z)=p(X,Y|θ)

(17)

完整数据的对数似然函数一般是在E步骤中进行的，这里X为已知量，那么针对未知变量Y的期望[12]用R函数表示：

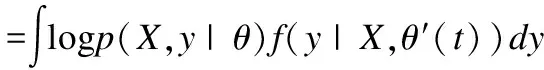
(18)

在M-step中，通过下式对模型参数进行更新处理：

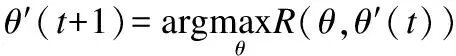
(19)

EM算法通常不断对E步与M步进行循环处理，直至参数达到收敛.它在理想状态下可获得局部最优化值[13].

EM能够适应不同的问题环境，为了充分考虑不同应用场景，统一表示成为：

y=Cx

(20)

其中，矢量y∈Rm×1代表测量数据，矢量x∈Rn×1代表观测对象密度分布估计值，矩阵C∈Rm×n代表映射矩阵.

考虑到大部分物理过程均为衰减过程，x与y均为非负矢量，然而矢量δU与δσ无法保证非负约束，为此，引入先验信息对δU进行计算：

δU=(-1)q(Umea-Uref)

(21)

其中，Uref用于描述理论测量值，Umea用于描述实际测量值.q值主要取决于先验信息(1.1节得到)，也就是如果Uref和Umea相比，Uref为较低的测量值，那么q=2；否则，q=1.

在上述非负约束先验信息下，将半监督机器学算法思想应用于EM算法的优化之中.

通常来讲，如图1所示，在EM算法的每次循环中.

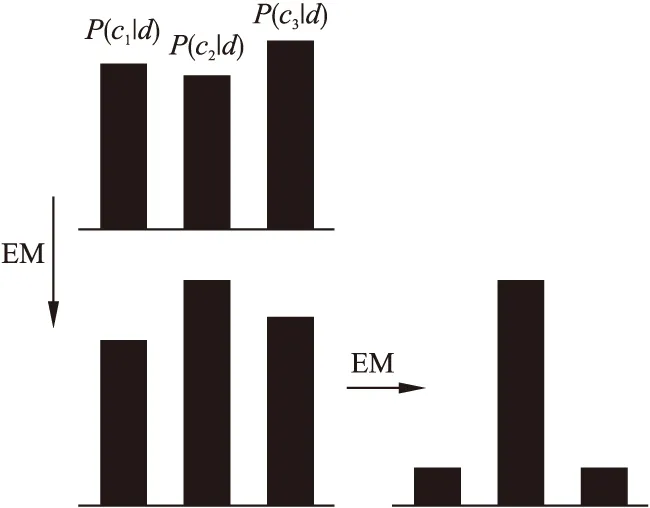
图1 EM算法迭代过程示意图Fig.1 Schematic diagram of iteration process of EM algorithm

设定没有标注样本di按照权重P(cj|di;θ′)分配，也就是在确定c*值的情况下，下一轮计算di也仅可用于占其P(c*|di;θ′)部分参与和c*的训练，并且需考虑其和其余类别相关P(cj|di;θ′)的可能性.EM算法不判断为标定样本量，从而导致陷入局部最优，且收敛速度变慢.在EM算法中，P(cj|di;θ′)一直非零，所以本和其它种类相关的未标注的信息也在很大程度上会以P(cj|di;θ′)的部分对其余训练产生干扰，导致陷入局部最优.

半监督机器学习方法在每次训练时，可把确定结果引入到当前标注样本集，使用已经得到的结果训练，达到较好的训练效果，这是一种自训练的方式，大大避免了局部最优化问题.

本节把这种半监督机器学习方法用于EM改进中，在每次迭代，按照E步骤所得结果标注确定的样本数据，M步骤训练新训练集下样本[14，15].使得每次迭代未标注样本集U逐步减小，加大迭代速度，并且防止干扰.所以针对当前刚被添加至标注样本集的文本di∈L，如图2所示，依据训练结果直接设置P(cj|di;θ′)∈{0,1}，其余信息不会对其它训练产生干扰.

本文给出半监督机器学习改进EM算法的方法，如下：

1)假设t=0.

2)定义θ′(0)=argmaxθP(θ|L).

3)当U!=∅时，执行E步骤，假设z′(t+1)=E[z|D;θ′(t)]，则有：

P(i*,j*)=argmax(i,j){zij|di∈U}

(22)

令L=L∪{(di*,lj*)}，U=U{di*}，针对j=1～|C|，令zi*j=0，否则zi*j*=1

4)那么M步有，θ′(t+1)=argmaxθP(θ|D;z′(t+1)).

5)令t=t+1，循环进行上述步骤，输出θ′(t).

本节使用半监督机器学习的方式，在每轮E步中都会选择zj中最大的zi*j*，同时把di*从U中删除，把(di*,lj*)添加至集合L，并且将zi*j(j≠j*)置0，将zi*j*置1.M-step在训练集上对θ′进行估计.事实上，每轮迭代不是只选择一个没有标注的样本进行标注，可依据差异原则，标注若干可标注样本，实现标注效率的大幅度提升.

半监督机器学习方法在每轮迭代过程中会将完全确定的未标注样本添加标签，放入标注样本集合，为后续训练提供高质量标注样本，大大减少循环次数，从而避免了局部最优化问题的发生，提高训练性能.

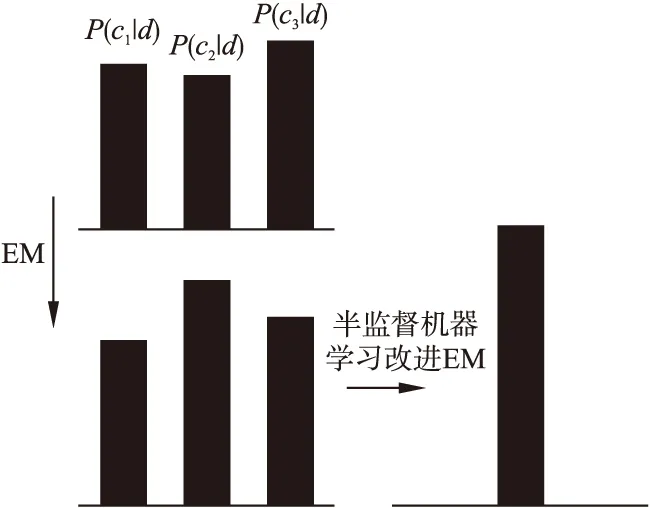
图2 改进EM过程示意图Fig.2 Modified EM process diagram

在上述分析的基础上，将最大似然方法引入，利用其对EM模型进行求解计算，构造下述似然函数：

(23)

上式中，λi=(Jδθ)i代表期望值.为了提高收敛速度，在似然函数中加入惩罚最小二乘，引入非负约束当成先验信息，转换成最小化问题：

(24)

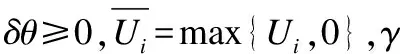
2.3 改进EM算法的应用

为更深入阐述本文优化方法，现使用本文优化后的方法对混合矩阵与高斯混合模型参数进行计算估量.

首先对混合矩阵进行剖析，x=[x1,x2,…,xd]T是d维随机变量，它概率密度函数可表示成：

(25)

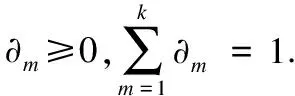
用θm代表某个变量的密度模型中的参数，通过各p(x|θm)，获取差异混合矩阵.混合矩阵全部参数集合可描述成θm={(∂m,θm)}.

混合高斯模型把各点出现的概率当成多个混合模型得到的结果，这是一种聚类的思维[16].混合高斯模型将每个模型经过加权处理之后，可得其概率密度函数[17]：

(26)

(27)

其中，πk代表权重，代表模型被选中概率，μk、∑k分别代表均值和方差.

使用最大似然函数[18]的方式对混合高斯模型进行训练，可表示成为：

(28)

针对上式及混合矩阵参数的直接求解非常困难，本节采用改进EM算法迭代训练获取.

给出有限标记训练样本集，用Gl={(X1,y1),…,(XL,yL)}进行描述，其中Xi代表某样本，该样本是高斯混合模型，yi代表对应类标.在整个训练样本集Gl中，共存在M个类型，因此有yi∈{c1,c2,…,cM}.

X=〈x1,x2,…,xN〉，xn∈Rd.针对各Sl中的(Xi,yi)，假设其均互相独立同分布，并假设针对未标记样本X，如果最大后验概率为P(cj|X)，那么j类中包含X，可通过类条件概率密度函数p(X|cj)与相关法则对后验概率进行求解：

(29)

式中，P(cj)代表先验概率.

(30)

针对于变量分类条件概率密度，使用混合高斯模型进行表示[19]，如公式(31)所示.

(31)

某一种混合变量的数量用K表示，混合权重用∂jk进行表示，使用p(x|μjk,∑jk)代表多元混合高斯模型的概率密度.

完整高斯混合模型，也就是X=〈x1,x2,…,xN〉的类条件概率密度可写成公式(32)的结构形式.

(32)

则可获取后验概率，P(cj|X)，令：

(33)

利用上述过程实现样本标记.

θj=(∂jk,μjk,∑jk)代表混合高斯模型，θm={(∂m,θm)}代表混合矩阵全部参数集合，使用EM算法对它们的参数进行估量，在半监督机器学习过程中，如果学习样本集包含两种不同的集合组，即：G=Gl∪Gu，可以为为标记和已标记两个组.

G={(x1,y1),…,(xl,yl),(xl+1,yl+1),…,(xl+1,yl+u)}

(34)

针对各未标记样本xi，对描述类别数量的M个隐含变量zij进行定义：

(35)

θj代表混合矩阵和混合高斯模型参数，使用改进之后的EM算法进行求解.其中，初始迭代参数θ0使用已经做过标注样本进行计算，再通过下述过程进行迭代：

对于未分类的样本，在E步骤中使用最大后验概率进行标记，通过公式(36)计算：

(36)

在M步骤中，按照所作标记的新样本使用最大似然对参数进行重新求解，得到新的结果.

基于上述过程，设计改进EM算法估计参数流程为：

1)假设t=0.

4)针对M步骤，令θl+1=argmaxθP(G,z(l+1)|θ).

5)令t=t+1，对以上步骤循环至收敛.

6)输出θl，需要注意的是，每一类的混合高斯模型的参数都是通过当前类别中的样本集进行估计的.

3 实验与分析

3.1 实验理论

对于EM算的局部最优化问题，主要原因为其初始值的设置不够合理.

在本次实验中，首先对EM算法的初始化值进行训练学习，同时，将传统方法作为对照实验组，与所提方法进行对比，并给出对比结果.

衡量算法有效性的另一个参数为算法拟合值，所谓算法拟合效果即算法能否按照原设定进行运算和应用.本次实验获取文献[4]算法、文献[6]算法以及所提算法的拟合曲线，具体获取方法如下：

将待测数据集H划分为两个子集H1与H2，其划分规则如下：将每个待测数据随机的划分到两个子集的其中任意一个中去.分别在两个观测样本子集H1，H2上将算法目标函数极大化，得到拟合值，并对多个拟合值进行整合，得到拟合曲线.利用拟合曲线可以看出算法的拟合效果，拟合的吻合程度越高，则说明实验方法的性能越高.

3.2 实验过程

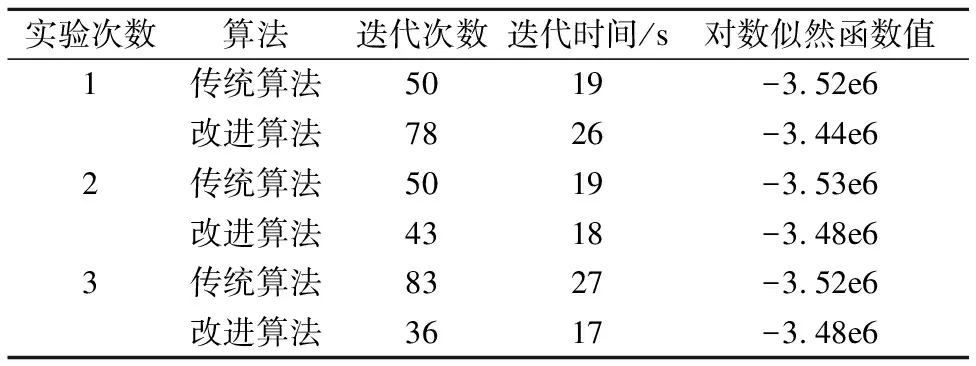
针对EM方法在执行过程中经常会经过很多次学习来筛选出最优的初始值.表1为传统方法和改进之后的方法性能对比.

分析表1可知，初始化相同的情况下，改进之后的方法对局部最优化问题起到了明显的抑制作用.

利用复合抽样法形成三阶数据，参数设置成，样本数量是2000个.样本采样序列以及理论曲线分别用图3和图4进行描述.

在进行实验过程中，本文分别将文献[4]方法和文献[6]方法作为对比进行参数估计，预设的研究模型的阶数是3，但本文方法模型阶数是4，这主要是由于复杂曲线可利用各种组成成分构成.

表1 传统方法和改进后的方法性能对比
Table 1 Performance comparison between traditional
method and improved method

实验次数算法迭代次数迭代时间/s对数似然函数值1传统算法5019-3.52e6改进算法7826-3.44e62传统算法5019-3.53e6改进算法4318-3.48e63传统算法8327-3.52e6改进算法3617-3.48e6

图3 样本采样序列Fig.3 Sample sampling sequence

010.008.006.004.002.0拟合值-20-100102030样本值图4 理论曲线Fig.4 Theoretical curve010.008.006.004.002.0拟合值-20-100102030样本值原始曲线本文方法拟合结果图5 本文方法拟合结果Fig.5 Fitting results of thismethod

为了将本文方法和文献[4]方法、文献[6]方法进行比较，也把这两种方法的阶数设置成6.本实验利用不同方法拟合曲线和原始曲线相比，替代参数估计值与设定值的比较，从而便于分析.

010.008.006.004.002.0拟合值-20-100102030样本值原始曲线文献[]4方法拟合结果图6 文献[4]方法拟合结果Fig.6 Fitting results ofdocument[4]010.008.006.004.002.0拟合值-20-100102030样本值原始曲线文献[6]方法拟合结果图7 文献[6]方法拟合结果Fig.7 Fitting results ofdocument[6]

采用本文方法、文献[4]方法、文献[6]方法进行拟合，得到的拟合曲线和原始曲线比较结果依次用图5、图6和图7进行描述.

本文实验样本数量较为充足，将不同样本初始条件划分成6类，针对6种初始条件，获取本文方法拟合结果和文献[4]方法、文献[6]方法相比的性能可通过表2进行描述.

表2 源信号处理前后功率谱峰值及对应频率
Table.2 Comparison of fitting performance of three methods

初始条件采用方法迭代次数/次迭代时间/s似然函数值初始条件1本文方法4215-3.46E+06文献[4]方法5323-3.59E+06文献[6]方法8235-3.56E+06初始条件2本文方法4919-3.47E+06文献[4]方法6828-3.61E+06文献[6]方法7533-3.58E+06初始条件3本文方法3812-3.49E+06文献[4]方法6531-3.55E+06文献[6]方法8925-3.59E+06初始条件4本文方法3220-3.46E+06文献[4]方法5139-3.54E+06文献[6]方法5551-3.62E+06初始条件5本文方法4518-3.49E+06文献[4]方法7237-3.59E+06文献[6]方法8842-3.53E+06初始条件6本文方法4113-3.49E+06文献[4]方法8921-3.62E+06文献[6]方法6036-3.65E+06

3.3 实验结果分析

综合分析不同方法拟合曲线和原始曲线比较结果可以看出，本文提出的基于半监督机器学习的改进EM算法得到的拟合曲线和原始曲线的重合程度比文献[4]方法、文献[6]方法明显更优，表明本文方法拟合性能明显高于其它两种方法，这主要是因为本文改进EM算法对传统EM算法容易陷入局部最优的弊端进行了有效的优化，使得本文方法得到的最优解和实际值更加吻合，而文献[4]方法、文献[6]方法无法解决传统EM算法容易陷入局部最优的问题，得到的解并非最优解，导致拟合精度低.

分析不同方法拟合性能可以看出，在初始化相同情况下，本文方法对模型容易进入局部最优的问题起到了明显的抑制作用，能够获取更优的拟合结果.不仅如此，本文方法迭代次数最少，迭代时间最短，整体性能优.

4 结 论

本文针对EM算法及其改进改进所存在的不足，使用半监督机器学习机制对其进行改进和优化.

使用二项分布概率函数以及惩罚概率定理以及，对最大似然函数进行描述，将惩罚因子加入到最大似然函数之中，大大降低了模型的最大似然估计的误差.

对EM算法实现过程进行分析，引入非负约束先验信息，针对EM算法很难在全局量空间中求解出最优解问题，结合半监督机器学习机制实现EM算法的优化改进，利用其中的一种自训练学习模式，在每次的训练的过程中，把确定标本放入到标记集合之中，经过自己所得到的结果进行训练，获得很好的训练结果，很好地避免了陷入局部最优.在此基础上，EM算法数学模型参数通过最大似然方法进行计算和优化，构造似然函数，在最大似然函数增加惩罚最小二乘因子，引入非负约束当成先验信息，转换成最小化问题.

仿真实验结果表明，本文所提的基于半监督机器学习模式的改进EM算法得到的拟合曲线和原始曲线的重合程度比其它方法明显更优，说明所提方法不会陷入局部最优，拟合性能好.除此之外，所提方法迭代次数最少，迭代时间最短，整体性能优.