模块化产品设计中模块间的关联分析与解耦策略

程贤福，万 冲，邱浩洋，万丽云

(华东交通大学 载运工具与装备教育部重点实验室，江西 南昌 330013)

0 引言

模块化设计是对一定范围内的相同功能不同性能，或是不同功能，以及不同规格的产品进行分析，划分出一系列功能结构模块，通过对产品模块进行重组，从而得到不同功能，或是不同性能的产品，以满足不同层次用户需求的一种方法[1]。模块化产品可以单独进行设计和维护，从而提高整体产品的可行性和可维护性，缩短产品的研发周期。在实际产品设计过程中，完全独立的模块是鲜见的，模块之间往往存在着相互作用，这将使得设计越来越复杂，进而增加产品开发周期和成本。因此模块化产品设计耦合应尽量予以避免，但由于技术或其他条件的限制，要想得到完全无耦合的模块往往是非常困难的。产品设计耦合问题受到了国内外学者的广泛关注，钟掘[2]针对复杂机电系统，较为全面地研究了耦合设计理论和方法。类似这种控制系统的耦合及解耦，其实质上是“场”与“场”之间的相互作用引起的。

Kang[3]提出将TRIZ冲突矩阵应用到公理设计中，选择合适的发明原理来对公理设计中的耦合进行解耦；Olaru等[4]基于可拓理论，提出一种解决设计过程中的精度—稳定性矛盾问题。檀润华[5]系统论述了TRIZ理论，并将其应用到产品设计中，为解决耦合冲突提供了一种有效方法。该理论主要解决产品设计中的冲突，即功能耦合。于学军[6]等基于网络分析法研究了功能要求之间的交互作用，提出了交互作用的测评算法及判断交互作用可否忽略的判别方法；肖人彬等[7]利用免疫算法对功能耦合关系进行聚类识别，通过解耦和割裂操作对耦合功能进行重组；彭翔等[8]基于敏感度计算和耦合特性分析，提出一种基于多重耦合聚类的复杂产品多变量关联设计模型分解方法；Cai等[9]采用系统创新思维模式描述耦合问题，选择并应用创新思维激励技术将关联的功能需求完全解耦；Yu等[10]基于功能—结构依赖关系分析，提出一种适应性机械系统的功能耦合分析方法。这些文献主要从产品设计中功能—结构映射角度探讨了耦合问题的。

Choi等[11]提出用流程图来表示系统结构，然后借助流程图分析各个模块之间的耦合关系。宋利伟等[12]针对模块间的耦合复杂性度量问题，提出了关系强度的量化指标。陈羽等[13]针对异构模块组合的耦合问题，提出了完全关联矩阵和基于进化策略的耦合分析方法，但未考虑零件的变更对关联模块的影响，也未涉及解耦操作。乔虎[14]利用设计结构矩阵(Design Structure Metrix,DSM)分析了参数的关联关系，预测了模块的可能变更路径，提出自适应模块的变更方法，其主要研究模块不同变更来源的应对策略。还有一些研究针对产品开发过程中耦合设计任务分配策略[15]、设计变更传播影响[16-17]及系统稳健性建模等，如程贤福[18]提出了在产品平台规划初期就开始考虑产品的稳健性和适应性，以避免后期出现大的返工。

以上方法主要针对产品设计中的功能耦合、零部件间耦合或耦合设计任务集协调等进行分析的，有些只进行了耦合分析并未提供解耦方法，目前较少针对模块间的耦合及解耦进行探讨。本文针对模块化产品设计中模块间的耦合关联问题，考虑模块间的接口因素和依赖零件所在的模块内部关联依赖关系，分析主控零件的关联传播路径，计算模块关联依赖度，提出相应的解耦策略。

1 模块间的关联依赖度分析

产品模块一般是根据零部件间的综合关联关系包括联接、功能和物理关联性来划分的。联接关联性表示两个零件几何结构上的关联性，主要考虑它们联接后拆卸的难易程度；功能关联性表示两个零件实现同一功能的关联性，主要考虑它们完成同一项功能的协同程度；物理关联性表示两个零件之间是否存在能量流、信息流或物料流的传递等物理关系，主要考虑一个零件的变化对另一个零件的影响程度。零部件之间的功能关联性和联接关联性相关矩阵为对称矩阵，物理关联性相关矩阵因两个零件间的物理传递特性不同，则相互关联性也可能不相同，其数值要小且尽可能为单向的。因此，产品的综合关联矩阵一般为非对称矩阵。从零部件设计变更传播和耦合的角度分析，零部件间的综合关联度大说明它们之间的关联关系强，但并不表示它们间的耦合就大。如螺栓和螺母，尽管它们关联性强，但螺母是根据螺栓的尺寸来确定的，也就是说，螺栓的变更会引起螺母的变化，反之不然。因此，本文基于产品已划分模块，考虑零部件间的关联依赖关系，确定它们之间的相互影响程度，建立产品模块关联依赖矩阵，从而为模块间的耦合分析及解耦提供支持。

模块间的耦合是由产品聚类块之外的关联元素引起的。模块内部的耦合分析是为了实现零部件的迭代顺序，而模块间的耦合分析则是为了评价模块间的关联程度、确定模块优先级顺序及控制与调整相应的零件。一般地，产品设计中任意两个模块间耦合的强弱可通过一个模块内的所有零件与另一个模块内所有零件的综合关联度来衡量。假设nk和mk分别是第k个模块中第一个零件和最后一个零件的序号，np和mp分别是第p个模块中第一个零件和最后一个零件的序号，r(i,j)为第i个零件Ci和第j个零件Cj间的综合关联度，则模块Mk和Mp之间的耦合度

(1)

耦合度越大，两个模块的关联关系越紧密。然而，模块间的耦合度不能体现两个模块相互间具体的关联依赖关系，即不能判断一个模块对另一个模块的依赖程度。

为了探讨模块间耦合关联问题的处理方法，通过DSM表示产品零件(以C表示)之间的关联关系，并以两个耦合模块之间的关系进行描述和分析，如图1所示。图中的对角线元素表示零件自身关联关系，模块内非对角线的元素表示零部件间的物理关联关系，其数值代表关联依赖程度。本例中，有两个元素A和B游离在两个耦合模块之外，说明两个模块并非独立的，它们之间存在相互作用。具体为左上角模块(模块1)中的C2影响右下角模块(模块2)中的C6以及模块2中的C7影响模块1的C3。显然，改变模块1会引起模块2的变化。同样，模块2的变化将造成模块1的变更。

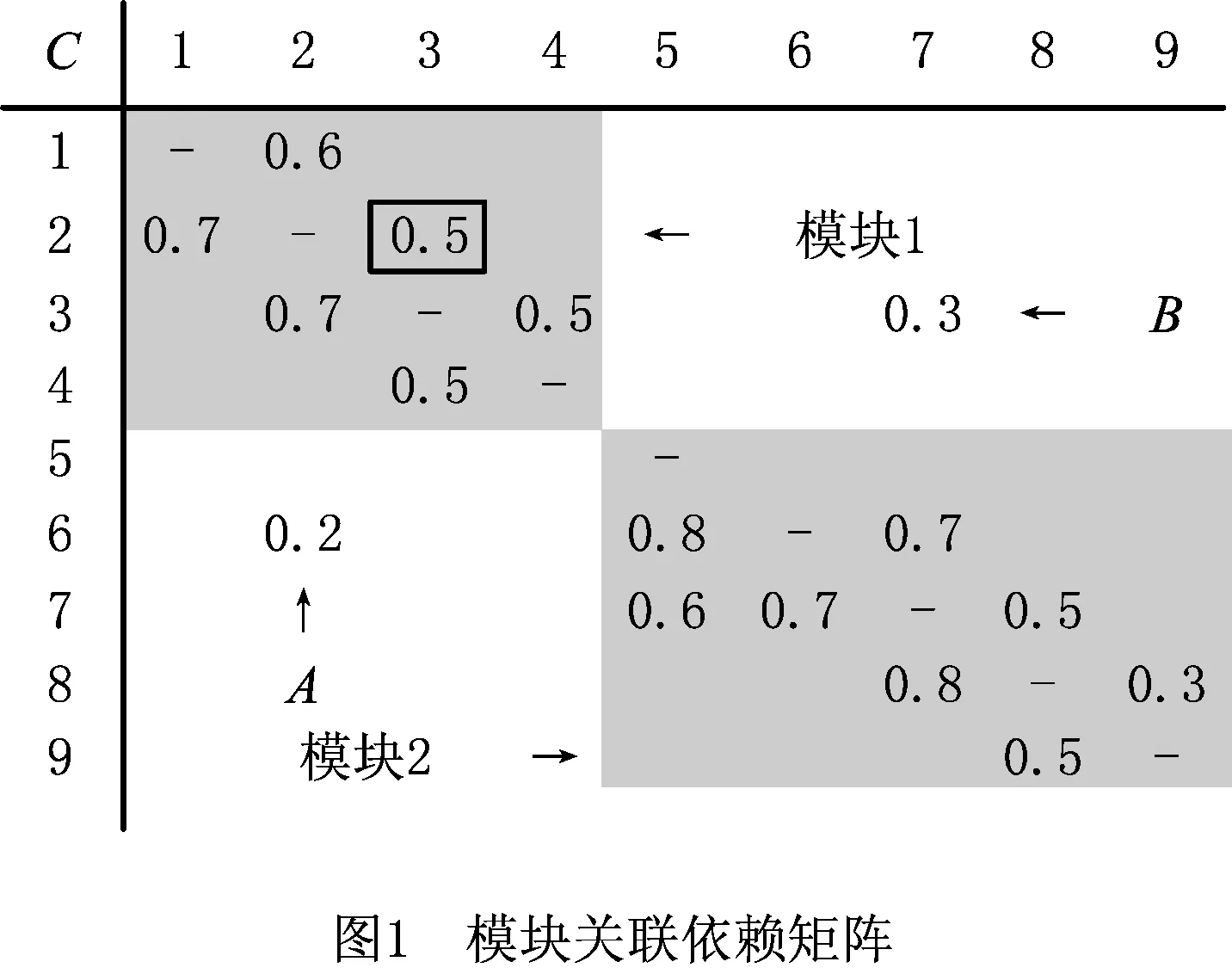
为了更直观表示模块间零件的关联关系，可以通过零件的关联传播路径来描述。图1所对应的零件关联传播路径如图2所示。此时，可根据关联传播路径分析一个模块影响另一个模块的详细情况，判断模块的关联依赖度大小，确定模块的优先级顺序。

由图1和图2可知，C2(模块1中)的变更会直接传播给C6(模块2中)，C6的变化又传播给同一模块内的C7，C7传播给C8，C8又传播给C9；同时C7、C8、C9和C6相互之间存在耦合，它们的变更又将反馈给C6，但不会传播给C5，即C2的变更会引起模块2中除C5以外的其他零件的扰动。同理，C7(模块2)的变化会直接传播给C3(模块1中)，而C3又与C1、C2和C4相互之间存在耦合，因此C7的变更会引起模块1中所有零件的扰动。

可以看出，一个模块对另一个模块的关联依赖度除了与模块间直接的关联元素有关，还与模块本身的零件间的耦合强弱有关。一般地，如果某产品的2个模块Mp和Mq之间存在耦合关联关系，具体为Mp中的Cpi影响Mq中的Cqj，则称Cpi为主控关联零件，Cqj为依赖关联零件。通过分析Cqj与Mq中其他零件的关联关系，确定Cpi在Mq中的传播路径，记Cpi到Mq间的关联传播路径为Cpi→Mq。因为在Cpi→Mq路径中，不仅Cqj依赖于Mp中的Cpi，Cpi的变化可能也会间接引起模块Mq中其他零件的变更。为了分析Cpi对Mq的影响，应考虑Mq对Cpi的关联依赖度，记为D(Mq→Cpi)。假设Mp有p个零件，Mq有q个零件，Cpi→Mq路径上有npq(≤q)个关联零件，则Mq对Cpi的关联依赖度

D(Mq→Cpi)=r(Cpi,Cqj)·

(2)

式中：r(Cpi,Cqj)为Cpi(Mp中)对Cqj(Mq中)的关联影响度，r(l,k)为Mq中第l个零件对第k个零件的关联影响度。

当Mq中有多个零件直接受Cpi的影响，如Mq中的Cqj1和Cqj2直接依赖于Cpi，且关联传播路径Cpi→Mq(Cqj1)和Cpi→Mq(Cqj2)上分别有npq1和npq2个零件，则Mq对Cpi的关联依赖度

(3)

此外，如果模块Mp内有w个直接影响模块Mq的主控关联零件，则模块Mq对模块Mp的关联依赖度

(4)

同理，可通过上述方式计算出D(Mp→Mq)，比较D(Mq→Mp)和D(MP→Mq)。如果D(Mq→Mp)>D(MP→Mq)，说明Mq对Mp的关联依赖度比Mp对Mq的关联依赖度更大，因此，在设计时模块Mp优先于模块Mq实现。

那么，对于如图1所示的两个模块耦合关联情况，两个模块相互之间只有1个零件直接影响对方。其中模块2中的C7的变更会传播给模块1中所有零件，根据上述的模块关联依赖度公式，则模块1对模块2的关联依赖度为D(M1→M2)=0.3×[1+(0.7+0.7+0.5+0.6+0.5+0.5)]=1.35。同理，可计算出模块2对模块1的关联依赖度D(M2→M1)=0.2×[1+(0.7+0.8+0.5+0.7+0.5+0.3)]=0.9。因此，D(M1→M2)>D(M2→M1)，在产品设计时考虑模块2的实现应先于模块1。

2 关联模块的解耦策略

产品的结构复杂性是影响产品零部件耦合的一个重要因素。结构复杂性与其内部零部件自身复杂性、零部件间的接口(与其对应的两个关联零件的物理联接、质量流、能量流和信息流有关)以及系统的拓扑结构有关[19]。系统的结构复杂性不仅取决于其内部关联关系，还与其如何被划分成模块及模块度有关[20]。由于本文探讨的是产品模块间的耦合关联问题，模块内部零部件的耦合关联不在研究范围之内。

当产品设计过程中模块之间存在耦合关联时，必须进行适当的处理，否则就会使得设计复杂化，引起不必要的设计迭代，甚至导致无法得到可行的满意解。通过耦合分析得到模块间的优先级顺序后，可进一步分析主控关联零件对设计目标的影响度，以控制或调整相应的零件。假设Ci和Cj分别为一个模块的主控零件和另一个模块的依赖零件，Mk是Cj所在的模块，Cpq是耦合关联路径Ci→Mk上其他的零件(Mk中)，yMk是Mk的响应，则yMk与Ci→Mk路径上关联零件的关系可以表示为

yMk=fMk(Ci,Cpq)。

(5)

式中fMk()是模块Mk的响应与关联零件之间的关联函数。

关联元素的存在表示两个模块有直接关联关系，为了减少模块间的耦合，提出以下的解耦策略。

(1)减少模块间的关联依赖度

减少模块间耦合关联的一种有效方法是降低依赖零件所在的模块对主控零件的关联依赖度D(Mq→Cpi)。根据式(1)～式(3)，可以从两个方面来处理耦合：①减少主控零件对依赖零件的自身直接关联影响度r(Ci,Cj)；②减少依赖模块中关联传播路径上零件的关联影响度，即减少DSM中关联传播路径上零件的非对角元素的值。这样一来，一个模块对另一个模块的关联依赖度会降低，模块间的关联将减弱。

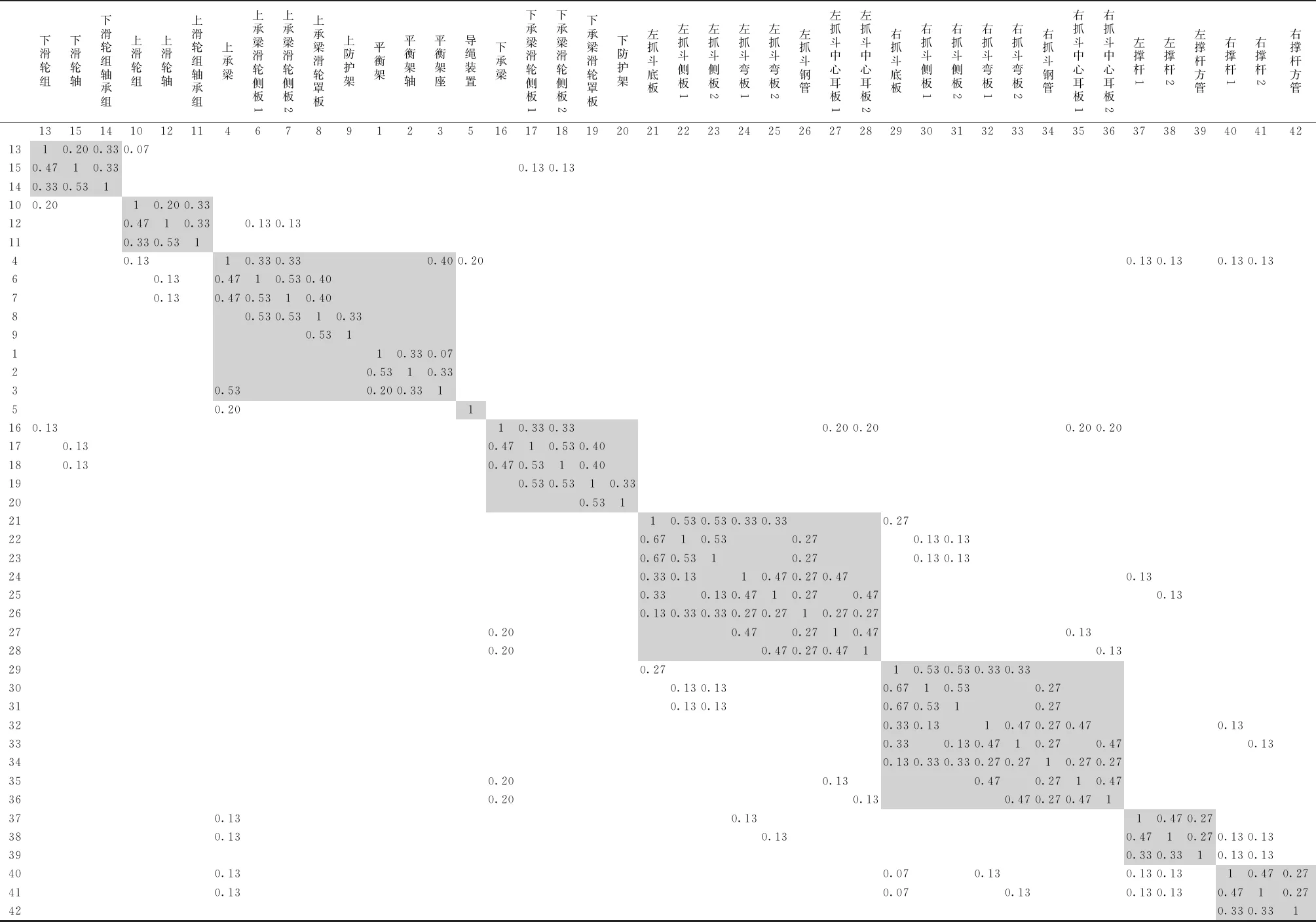
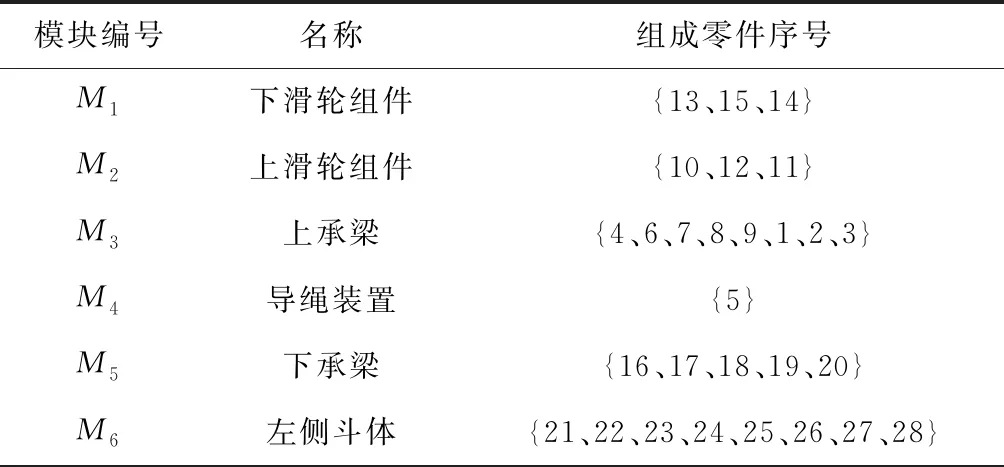
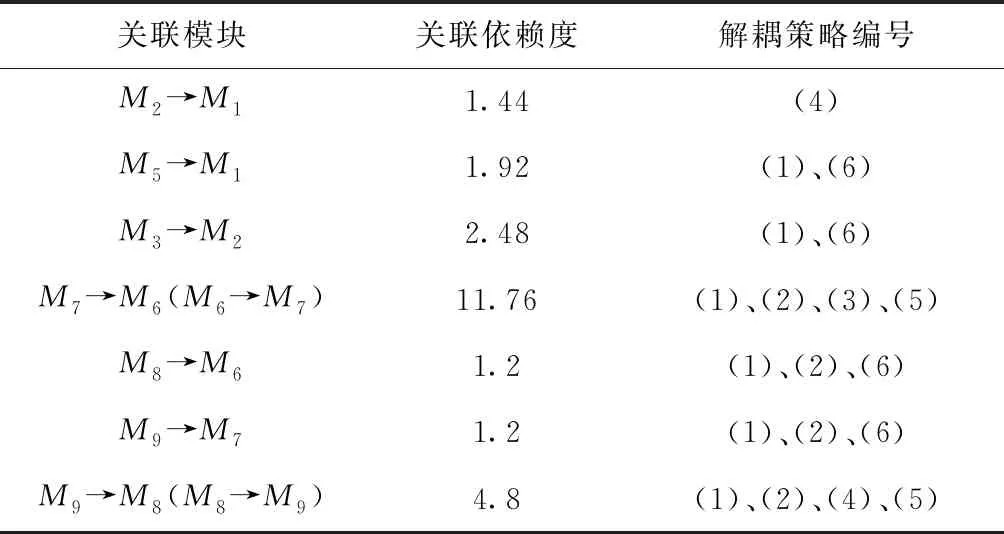
如图1所示，模块1中C2的变化将传播到C6，从而导致模块2的改变。M2→C2路径上还包括C7、C8和C9，要减少D(M2→C2)的值，除了减少r(C2,C6)外，还可以减少C6、C7、C8和C9四个零件之间的关联。如果r′(C2,C6)=0.1，r′(C6,C7)=r′(C7,C6)=0.4，则D′(M2→M1)=0.1×[1+(0.4+0.8+0.5+0.4+0.5+0.3)]=0.39

因此，减少主控零件对依赖零件的直接关联影响度和关联传播路径上零件的关联影响度可以比较有效地减少模块间的关联依赖度。

(2)减少关联零件变更传播的影响

产品模块关联零件之间的设计变更不仅存在直接依赖，还存在间接依赖。这样，一个模块中某零件的设计变更可能会影响其关联零件所对应模块中其他零件的设计，从而造成产品开发时间成本的上升。可以通过广义链表结构或DSM及图论中邻接矩阵来描述这种设计变更影响。

一种有效的方法就是减少传播路径中的某个或几个影响强联通的关联元素。比如图1和图2中，模块2中C7的变更直接影响模块1的C3，继而传播给C2、C4和C1。C1、C2和C3形成了耦合，C3和C4也形成了耦合，前者相对后者耦合程度更大。如果能减少或切断C3对C2的传播影响(图1中方框位置)，则仅C4间接依赖C7，C2和C1就不会或很少依赖C7。如果r(C2,C3)=0，则D′(M1→M2)=0.3×[1+(0.5+0.5)]=0.6

同时，也可以计算出模块1中其他关联元素变化后模块1对模块2的依赖度：

当r(C1,C2)=0，则D′(M1→M2)=0.3×[1+(0.5+0.7+0.5+0.5)]=0.96；

当r(C2,C1)=0，则D′(M1→M2)=0.3×[1+(0.5+0.7+0.6+0.5+0.5)]=1.14；

当r(C3,C2)=0，则D′(M1→M2)=0.3×[1+(0.5+0.6+0.7+0.5+0.5)]=1.14；

当r(C3,C4)=0，则D′(M1→M2)=0.3×[1+(0.5+0.6+0.7+0.7+0.5)]=1.2；

当r(C4,C3)=0，则D′(M1→M2)=0.3×[1+(0.5+0.6+0.7+0.7)]=1.05。

显然，在关联路径上，r(C2,C3)对D(M1→M2)的影响最大，它是影响强联通的关联元素，要尽可能减少它的影响。

(3)减少依赖零件在模块中的影响

假设模块Ml和Mk之间存在一个关联元素，即Ml中的C0影响Mk中的C1，则C0是主控零件，C1是依赖零件。Mk由C1、C2、C3和C4组成。如果C1对Mk的影响最小，即

可以判断，C1在模块中是一个弱影响的零件，其影响可以忽略不计。此时，认为Ml对Mk的影响是不显著的。因此，可以通过减少依赖零件在相应模块中的影响或增强其他零件在相应模块中的影响来减弱耦合。

如图1和图2所示，模块2有5个零件，从零件关联影响度和传播路径可以看出，模块内部零件的优先次序为C5、C6、C7、C8和C9。其中C5的影响最大，它直接影响C6和C7，而不依赖于模块2中其他零件。C9的影响最小。如果降低依赖零件C6在模块中的地位或依赖零件为C9，则可以削弱两个模块之间的耦合。

(4)关联零件的合理匹配

根据解耦控制系统设计中被控变量和操纵变量的匹配思想[2]，对于关联元素对应的两个关联参数(即主控零件和依赖零件)，例如图1中关联元素C(2,6)对应的两个零件C2和C6，分析主控零件和依赖零件(C2→C6)相对增益量，判断关联参数间的关联程度，通过选择关联参数的合理匹配，使得两者间的关联最小，从而可以减少模块间的耦合。

匹配主要针对两关联的零件接口，如机械设备中常用到的梅花联轴器，当输入端(如减速器)尺寸在一定范围内变化，输出端(如制动器等)尺寸可以不改变，只需重新匹配联轴器和减速器即可，因为联轴器两端的孔径可以不同。

有时因主控零件与依赖零件及模块中的其他零件关联紧密或某种约束机制导致无法找到直接的参数匹配时，此时可以考虑将主控零件与依赖零件及其关联的零件适当组合，也可能找到较佳的匹配。如图1所示，模块1中的C2影响模块2中的C6，后者又与C7、C8和C9关联，如果不能直接匹配C2和C6，可以考虑组合C6、C7、C8和C9，再与C2匹配。

(5)控制主控零件的变差

减少模块间耦合的另一种有效的方法是通过控制主控零件的变差来减少其传播影响，并根据主控零件所在模块内部零件综合关联关系合理确定其变动范围。

假设主控零件Ci的变差为ΔCi，对应模块关联路径上某相关零件Cp的变差为ΔCp，可以利用一阶泰勒近似方法，忽略高阶项，则式(5)线性近似于下式：

(6)

式中ΔyMk()是模块Mk的响应变差。

(6)提高模块的适应性

利用适应性设计，使模块接口参数具有一定的适应能力，提高模块自身的柔性。因为适应性参数具备一定范围内变动的能力，在不破坏产品拓扑结构前提下，数值可在一定约束范围内变动。比如，可以结合公理设计，通过分析产品的功能要求并将其映射为设计参数，使之满足独立公理；或者当某个功能要求变更时，对应的关键设计参数的变化与非对应的设计参数的变化比较而言更显著，设计参数的适应性就越好。如滑轮的卷绕直径D0是由钢丝绳直径d和工作级别而定，为了提高钢丝绳寿命，应满足D0>h·d，h为系数，与工作级别和钢丝绳结构有关。

当d=20 mm，h=18时，D0 min=360 mm。在设计滑轮时，可以取D0=400 mm，这样可以适应一定范围内钢丝绳和工作级别的变化。

3 实例分析

本章以某型号起重机抓斗为例，对其模块间的耦合进行分析与解耦。该抓斗包括42个主要零部件，其结构及零件如图3所示。分析各零部件间的联接、功能和物理关联性，确定它们的综合关联度。然后建立抓斗的设计结构矩阵，基于密度聚类算法[21]，以模块高内聚度和模块间低耦合度为划分准则，对DSM进行聚类重组，得到如图4所示的9个模块，各模块的名称及所包含零件序号如表1所示。由于本文主要讨论模块间的关联依赖关系及解耦，具体的模块聚类过程不在此进行展开，另文阐述。

下滑轮组下滑轮轴下滑轮组轴承组上滑轮组上滑轮轴上滑轮组轴承组上承梁上承梁滑轮侧板1上承梁滑轮侧板2上承梁滑轮罩板上防护架平衡架平衡架轴平衡架座导绳装置下承梁下承梁滑轮侧板1下承梁滑轮侧板2下承梁滑轮罩板下防护架左抓斗底板左抓斗侧板1左抓斗侧板2左抓斗弯板1左抓斗弯板2左抓斗钢管左抓斗中心耳板1左抓斗中心耳板2右抓斗底板右抓斗侧板1右抓斗侧板2右抓斗弯板1右抓斗弯板2右抓斗钢管右抓斗中心耳板1右抓斗中心耳板2左撑杆1左撑杆2左撑杆方管右撑杆1右撑杆2右撑杆方管1315141012114678912351617181920212223242526272829303132333435363738394041421310.200.330.07150.4710.330.130.13140.330.531100.2010.200.33120.4710.330.130.13110.330.53140.1310.330.330.400.200.130.130.130.1360.130.4710.530.4070.130.470.5310.4080.530.5310.3390.531110.330.0720.5310.3330.530.200.33150.201160.1310.330.330.200.200.200.20170.130.4710.530.40180.130.470.5310.40190.530.5310.33200.5312110.530.530.330.330.27220.6710.530.270.130.13230.670.5310.270.130.13240.330.1310.470.270.470.13250.330.130.4710.270.470.13260.130.330.330.270.2710.270.27270.200.470.2710.470.13280.200.470.270.4710.13290.2710.530.530.330.33300.130.130.6710.530.27310.130.130.670.5310.27320.330.1310.470.270.470.13330.330.130.4710.270.470.13340.130.330.330.270.2710.270.27350.200.130.470.2710.47360.200.130.470.270.471370.130.1310.470.27380.130.130.4710.270.130.13390.330.3310.130.13400.130.070.130.130.1310.470.27410.130.070.130.130.130.4710.27420.330.331

图4 某型号起重机抓斗模块聚类结果

表1 抓斗的模块编号、名称及其组成零件序号

续表1

然后考虑零部件间的依赖关系，确定它们间的相互影响程度，建立抓斗模块关联矩阵。如图5所示。可以看出，只有部分模块之间存在耦合关联，而并非任意两两模块之间都有关联。

C131514101211467891235161718192021222324252627282930313233343536373839404142131150.81140.61100.61120.81110.6140.4160.410.870.40.8180.40.4190.611120.6130.40.4151160.41170.410.8180.40.81190.40.41200.612110.20.20.4220.610.80.20.2230.60.810.20.2240.410.80.2250.40.810.2260.40.20.21270.210.8280.20.81290.410.20.2300.20.20.610.8310.20.20.60.81320.410.80.2330.40.810.2340.40.20.21350.210.8360.20.81370.210.8380.20.810.40.4390.20.210.40.4400.20.40.410.8410.20.40.40.81420.20.21

图5 某型号抓斗模块关联依赖矩阵

根据式(2)～式(4)，可以计算出抓斗两两模块之间的关联依赖度，分别为：

D(M2→M1)=0.6×[1+(0.8+0.6)]

=1.44，D(M5→M1)=1.92;

D(M3→M2)=2.48；

D(M7→M6)=D(M6→M7)=11.76；

D(M8→M6)=1.2，D(M9→M7)=1.2；

D(M9→M8)=D(M8→M9)=4.8。

从上述计算可以看出，模块1影响模块2和模块5，但不依赖于任何模块，它为先行模块。模块2影响模块3、模块6和7耦合关联(结构对称关系)，模块8和9也是结构对称而相互关联，且为接收模块。因此，模块的优先级顺序为，M1→M2→M3、M4→M5→M6、M7→M8、M9。下面具体分析各模块间的耦合情况。

模块2的C10(上滑轮组)依赖于模块1的C13(下滑轮组)。下滑轮组是动滑轮组，是根据倍率和钢丝绳确定的。上滑轮组是定滑轮组，由下滑轮组而定。两者关联紧密，很难从影响度或传播关系方面减少耦合，但可通过匹配上、下滑轮的个数和大小而不影响滑轮轴承来减弱关联。

模块5的C16(下承梁)依赖于模块1的C13(下滑轮组)，下滑轮组的大小会影响下承梁的结构，继而影响下承梁滑轮侧板。提高下承梁适应下滑轮组变动的能力以减少下滑轮组对下承梁的直接影响度，同时通过安装调整使两边的下承梁滑轮侧板关联性也降低。如当r′(C13,C10)=0.2，r′(C17,C18)=r′(C18,C17)=0.4，则D′(M5→M1)=0.2×[1+(0.4+0.4+0.4+0.4+0.4+0.4+0.6)]=0.8

模块3的C10(上承梁)依赖于模块2的C10(上滑轮组)，其关联性质同上。

模块6和模块7因结构的对称和功能一致关系而耦合，相互间的关联依赖度是一样的。从功能上可视作一体，因此可等同视为一种模块内部的耦合，在抓斗设计时只需考虑左侧或右侧斗体的一侧即可。由于这两个模块内零件数相对较多，模块间联系较紧密，为了减少它们之间的耦合，应控制关联零件的变差、减少模块间的关联依赖度、减少关联零件变更传播的影响以及减少依赖零件在模块中的影响。

模块8和模块9也是因结构的对称和功能一致关系而相互关联，其性质同模块6和模块7的耦合关联。但因为零件数少，依赖零件地位就影响不突出。同时两侧撑杆的合理匹配也是一种策略。

模块8依赖模块6，其关联依赖度较小，主要从模块8内部零件的自身关联性考虑。如为了减少变形，每侧的其中一根撑杆安装在抓斗头部或鄂板上时可以调整，这样会减少2根撑杆的相互关联。C37对C38的影响度降到0.5，C38对C37的反馈影响度降到0.3，则D′(M8→M6)=0.88

模块9依赖于模块7，其关联性质同模块8依赖于模块6。

上述关联模块间的依赖度及所采用对应的解耦策略如表2所示。

表2 模块间的关联依赖度及对应的解耦策略

4 结束语

产品模块化设计与产品物理结构间相互影响程度有着密切关系，在实际的产品设计过程中，完全独立的模块是鲜见的，模块之间往往存在着耦合关联关系，这将引起设计的迭代，使得设计越来越复杂，进而增加产品开发周期和成本。为了探讨模块间耦合关联问题的处理方法，以DSM表示产品零件之间的关联关系。通过对DSM聚类得到模块，正是聚类块之外的关联元素导致了模块间耦合关联。为了更直观表示模块间零件的关联关系，通过零件的关联传播路径来描述，分析一个模块中的关联零件对另一个模块的影响，计算模块关联依赖度，确定模块优先级顺序。

当产品设计过程中模块之间存在耦合关联时，进一步分析主控关联零件对设计目标的影响，控制与调整相应的设计参数。根据产品结构及零部件的复杂性，基于零件关联传播分析，提出相应的解耦策略，包括减少模块间的关联依赖度、减少关联零件变更传播的影响、减少依赖零件在模块中的影响、关联零件的合理匹配、控制主控零件的变差及提高模块的适应性等。

最后，以起重机抓斗模块化设计为例，分析了模块间的关联关系，讨论了相应的解耦方法，可提高抓斗的设计效率，也为产品的模块化设计提供了一种新的研究思路。下一步将研究模块间直接和间接变更传播的集成影响，识别模块变更所有可能的传播路径，计算模块变更的影响度。