双重不确定条件下危险品运输的多目标优化
2020-05-08刘亿鑫朱小林
刘亿鑫,朱小林,2+
(1.上海海事大学 物流科学与工程研究院,上海 201306; 2.上海海事大学 文理学院,上海 201306)
0 引言
随着国家化工、物流行业的不断发展,对危险品运输的需求量不断增加,在危险品运输过程中如果发生事故,将造成巨大的伤亡,为社会公共安全带来严重威胁,如何保证危险品运输车辆的交通安全,成为安全监管工作的重中之重。目前,国内外学者对危险品运输优化问题已经有一定的研究,针对危险品运输路线问题大多从最短路问题及车辆路径问题(Vehicle Routing Problem, VRP)两个方面进行优化。Xie等[1]考虑多式联运网络中危险品的运输,提出一种同时优化调车选址和运输路线的多模式危险品模型。柴获等[2]针对危险品车辆路径优化问题构建了多目标优化模型,并提出一种基于概率模型的进化算法进行求解。袁文燕等[3]针对危险品VRP构建了新的双目标优化模型,风险因素考虑了危险品载货量所造成的影响范围,并采用蚁群算法进行求解。杨立娟等[4]建立了有关静态单点多目标约束条件下危险品道路运输优化模型,运用灰色关联分析法选出与“绝对最优路线”关联度最大的次优路线。杨信丰[5]等考虑影响路段属性的不同因素,构建了时间依赖网络的城市危险品路径优化模型,并设计了标号求解算法进行求解。Bronfman等[6]将人口中心数量与到运输路径最近距离的关系作为安全系数,构建了双目标优化模型,并设计启发式算法对模型进行求解。刘海博等[7]提出一种基于小生境粒子群算法的公差多目标优化方法来解决多目标优化问题。Pradhananga等[8]构建了带时间窗的VRP双目标优化模型,并设计了元启发式算法求解。Bula等[9]考虑将风险最低作为目标,采用变邻域搜索法对危险品VRP进行求解。Toumazis[10]等考虑事故概率和事故后果的时间依赖性的情况下,将风险价值(value-at-risk, CVaR)的方法应用于危险品运输。上述研究主要是针对确定性网络的双目标优化,且针对多目标问题的解决方式大多为线性加权和法,而该方法通常采用主观权重,客观性较差,本文则在此基础上结合Pareto理论采用混合多目标粒子群算法对多目标问题进行求解。
在实际网络中危险品物流系统所得的信息往往是不确定的。危险品需求量、人口数量、影响范围等数据会受时间,路况等影响产生动态变化,而由于危险品运输的特殊性,运输路线的制定需严格遵守监管部门的规定,一般不会轻易更改。因此,研究不确定性条件下的危险品路径优化,并考虑路线的稳定性更符合实际需求。麻存瑞等[11]采用Bertsimas鲁棒离散优化理论,建立了危险品运输路径鲁棒优化模型,并采用改进遗传算法进行求解。费翔等[12]考虑不确定性需求下危险品运输路径优化问题,构建了随机优化模型,并采用粒子群算法进行求解。Mohammadi等[13]构建不确定下多式联运及轴幅式网络模型,采用元启发式算法进行求解。Mahmoudabadi[14-15]将危险品运输风险定义为一个混乱的因素,使用动态风险改变所选择的路线和优化的位置以构建配送中心。Garrido等[16]将资产概念纳入到风险的空间分布中,开发新的具有公平约束的多产品危险品运输优化模型。Mahmoudsoltani等[17]将模型中的风险环境定义为模糊环境,并采用多种多目标进化算法进行测试。Hu[18]等研究了需求和旅行时间双重不确定条件下具有硬时间窗的鲁棒车辆路径问题。Jiang等[19]根据研究一种同时优化调车场和运输路线位置的多模式危险品优化模型,构建了模糊不确定性模型。上述文献主要通过构建鲁邦优化模型和模糊数学模型来解决危险品运输的不确定性问题,并且大多为单一不确定性条件下的危险品运输路径优化。
综上所述,目前研究对于不确定条件下的危险品路径优化较少,且集中于模糊数学模型。本文则以风险最低和成本最低为目标,构建终端需求量和人口中心双重不确定条件下的随机优化模型;设计改进的多目标粒子群算法(Improved Muti-Objective Particle Swarm Optimization,IMOPSO)对模型进行求解,搜寻Pareto解集,为危险品运输问题提供可行的运输路径方案;最后,设计了算例对模型和算法的合理性和有效性进行验证,并进一步进行了不同样本规模下的稳定性分析以及对不确定性条件进行了灵敏度分析。
1 危险品运输随机优化模型建立
危险品物流系统的不确定性主要表现在运输过程中危险化学品本身的危险性、对环境的影响、运输事故及其扩散等,还表现在由于需求的不确定性和信息的不确定性引发的危险化学品物流的不确定性,危险品运输过程则需要在不确定条件下考虑降低事故的发生概率以及由于危险品爆炸或泄露造成的人员影响范围。因此,笔者设计以人口中心与危险品需求量为随机变量,以运输风险系数及运输成本最低为目标的随机优化模型。
危险品车辆根据终端随机需求量从起点运输至终点。设无向带权图G(N,P)为一个运输网络;I表示运输网络中所有节点的集合;P表示车辆从起点(O∈N)到终点(D∈N)所有可行路径的集合;(i,j)表示节点间路段,则i,j∈N,(i,j)∈P,p∈P表示路径集合P中一条可运输路线;Q为一定样本规模下的终端需求量,q为从样本规模中取出的终端需求量;W表示一定样本规模的人口中心,w为从样本规模中取出的人口中心;λij为路段(i,j)的事故概率;λijt为疲劳驾驶造成的事故概率;λijp为车辆泄漏造成的事故概率;tp为所选路径p总运输时间;tij为路段(i,j)的运输时间;θ1和θ2为加权因子;R为所有集中人口中心的集合,则r为一个人口中心,r∈R;zijr为暴露的人口中心造成的风险系数;zijb为需求量造成的风险系数;dijr为人口中心r到附近路段(i,j)的最短距离;B为根据样本规模下终端需求量Q所对应的车辆的载货量,b为从样本规模中取出的载货量;bmax为满载量,ϑ为车辆产生的固定成本;cijb为危险品运输过程中产生的成本;η为满载量下危险品运输所需成本;δ为标准安全距离;M为危险品种类集合,m为一个危险品种类,m∈M;γm为满载量下危险品m运输产生事故的影响范围;Xij(W,Q)为0-1变量,即在样本规模条件下所选择经过的路段(i,j)。
为简化随机优化模型,对运输网络提出如下假设条件:①根据危险品终端需求,每次危险品载货量与需求量相等,需求量小于满载量,满足供需平衡;②危险品运输时车辆速度仅考虑为匀速直线,不考虑在经过节点时的减速影响或是堵车等情况下对运输速度的影响以及发生事故的概率;③考虑多种不同种类的危险品,但由于其特殊性同时运输可能进一步造成危害,每次只运输一种危险品;④危险品的风险与其运输时间成正比例的关系,即危险品运输过程中不会随时间的增长导致呈爆炸性增长;⑤只考虑人口集中数量的变化,其区域位置固定,不会因人口流动而改变。
1.1 运输风险系数分析
危险品运输风险存在多种计算方式,一般考虑为发生事故与影响人数的乘积作为风险值,在此基础上,本文危险品运输风险系数影响因素主要考虑为运输事故率、人口风险和终端需求量3个方面,并以此对模型进行改进。
(1)运输事故率
运输事故率及运输过程中发生事故的概率,一般来说与路况、季节、驾驶经验、危险品车辆泄露、运输时间等因素相关。目前,国内80%左右的交通事故与驾驶员有关,在长途运输过程中驾驶员的精神不集中将导致交通事故的发生,根据《道路交通安全法实施条例》,当行驶超过4小时为疲劳驾驶。则本文中考虑危险品车辆泄露、运输时间作为影响因素,构建如下表达式:
(1)
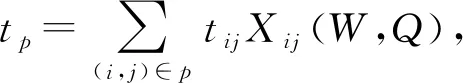
(2)人口风险
在危险品运输过程中,人员伤亡是危险品运输过程中尤为重要的评定因素,运输过程中应尽可能避开商场、居民区、学校、办公区等人口密集区域,这些密集区域的人口数量可能因为时间、季节、活动产生变化,本文设定密集区域固定不变,将人口数量作为不确定因素,引用Bronfman等[20]提出的风险定义,将道路经过流动的人口简化为人口集中区域,以该密集区域人口数量与到附近路段的最短距离之比作为该路段人口的风险系数,当到附近路段的最短距离大于标准安全距离δ时,风险系数为0;R表示所有集中人口中心的集合,r为一个人口中心,r∈R;W表示一定样本规模的人口中心,设定集中人口服从正态分布W~N(μ,σ2),w表示从样本规模中取出的集中人口数量。则针对每条路段的人口风险因素的表达式如下:
(2)
式中:zijr为暴露的人口中心造成的风险系数,dijr为人口中心r到附近路段(i,j)的最短距离。
(3)终端需求量
危险品运输事故影响范围与危险品运输载货量存在着密不可分的关系,需求的不确定性和信息的不确定性引发了危险化学品物流的不确定性。结合以上考虑,将危险品终端需求量作为不确定因素,B为根据样本规模下终端需求量Q所对应的车辆的载货量,b为从样本规模中取出的载货量,b∈B。则每条路段终端需求量风险系数的表达式如下:
(3)
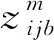
1.2 运输成本分析
运输成本考虑因素包括车辆维护、人员工资等固定成本,还包括车辆油耗、车辆载重量等不确定性成本。综合以上考虑,设运输过程中固定成本为ϑ,设车辆载货量与成本系数的表达式如下:
(4)
式中:cijb为危险品运输过程中产生的成本,ηm为满载量下危险品m所需的运输成本。
1.3 危险品运输随机优化模型
根据上述风险系数表达式及运输成本表达式,构建有容量约束下的危险品运输随机优化模型如下:
minE(Zp(W,Q));
(5)
minE(Cp(W,Q));
(6)
(7)
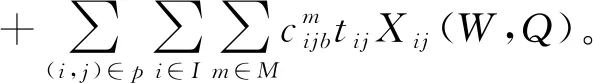
(8)
s.t.
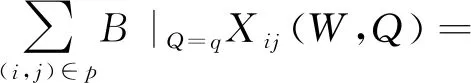
(9)
(10)
(11)
i∈N
(12)
(13)
Xij(W,Q)∈{0,1};
(14)
∀(i,j)∈P,∀r∈R,∀p∈P。
(15)
式(5)~式(8)为目标函数,其中:式(5)和式(6)表示运输风险系数和运输成本在样本规模下的最小期望;式(7)和式(8)表示在双重随机条件下的目标函数。式(9)~式(15)为约束条件,其中:式(9)表示运输路线的供需平衡;式(10)表示最大载货量约束;式(11)~式(13)代表路径平衡,其中:式(14)表示决策变量Xij(W,Q)为0,1约束,即在随机条件下输路径选择该路段为1,不选择为0,式(15)表示为决策变量的取值范围。
2 改进的多目标粒子群优化算法设计
粒子群优化(Particle Swarm Optimization,PSO)算法作为一种进化算法,具有实现容易、精度高、收敛快等特点。在解决多目标优化问题中,粒子群算法也具有很高的计算效率和执行速度,且粒子群算法不依赖问题的函数特征和解的形式。因此,本文采用混合多目标粒子群算法来对多目标优化问题进行求解,通过高效的群集来并行地对非劣解进行搜索,以构建非劣解集。
虽然粒子群算法具有上述优点,但其仍然存在容易陷入局部最优的问题[21]。为改进算法,本文采用自适应惯性权重,融入混合遗传算法中的交叉变异操作以及基于动态拥挤距离的精英解集更新对算法进行进一步的改进,以尽可能解决陷入局部最优的问题。
2.1 编码及解码设计
本文采用基于优先级的编码及解码方式。由于研究对象为无向运输网络,则赋予粒子每个维度(即每个节点)一个随机权重来进行解码。具体路径编码及解码步骤如下:
步骤1赋予随机权重。在粒子的每个维度上得到一个随机实数作为其权重,组成一个搜索路径的粒子。
步骤2判定路径优先级。根据邻接矩阵确定每个节点之间的连接关系,根据邻接矩阵连接为1,不连接为0,对于连接的点,由起点开始选择节点权值中最大的节点放入路径,并依次选择其他节点,组成路径。在选择过程中,为了进一步增加效率,提高成功率,将已经过的节点标记为1,并确定最大退步次数为St,即路段(i,j)中j-i<-St,则不再经过这些节点。
步骤3计算粒子适应度值。根据已经得到的路径,计算其所在路径的适应度值。若所得路径为起点O—终点D,则计算所选路段的两个适应度值,即风险与成本;所得路径不为起点O—终点D,则赋予该路径的适应度值为无穷大。
步骤4更新迭代。根据所提出的算法进行运算,更新粒子在每个维度上的权重,计算新的适应度值。
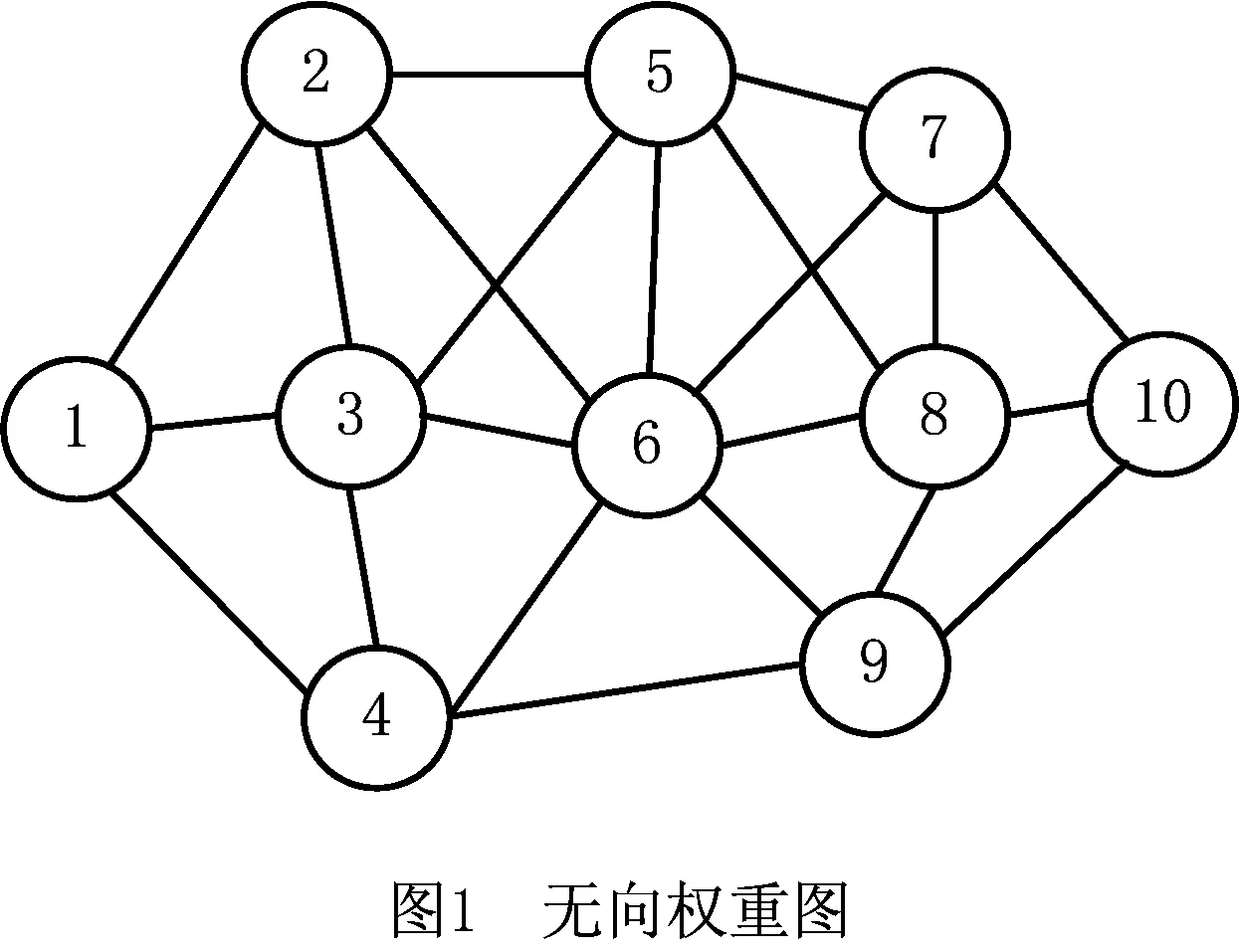
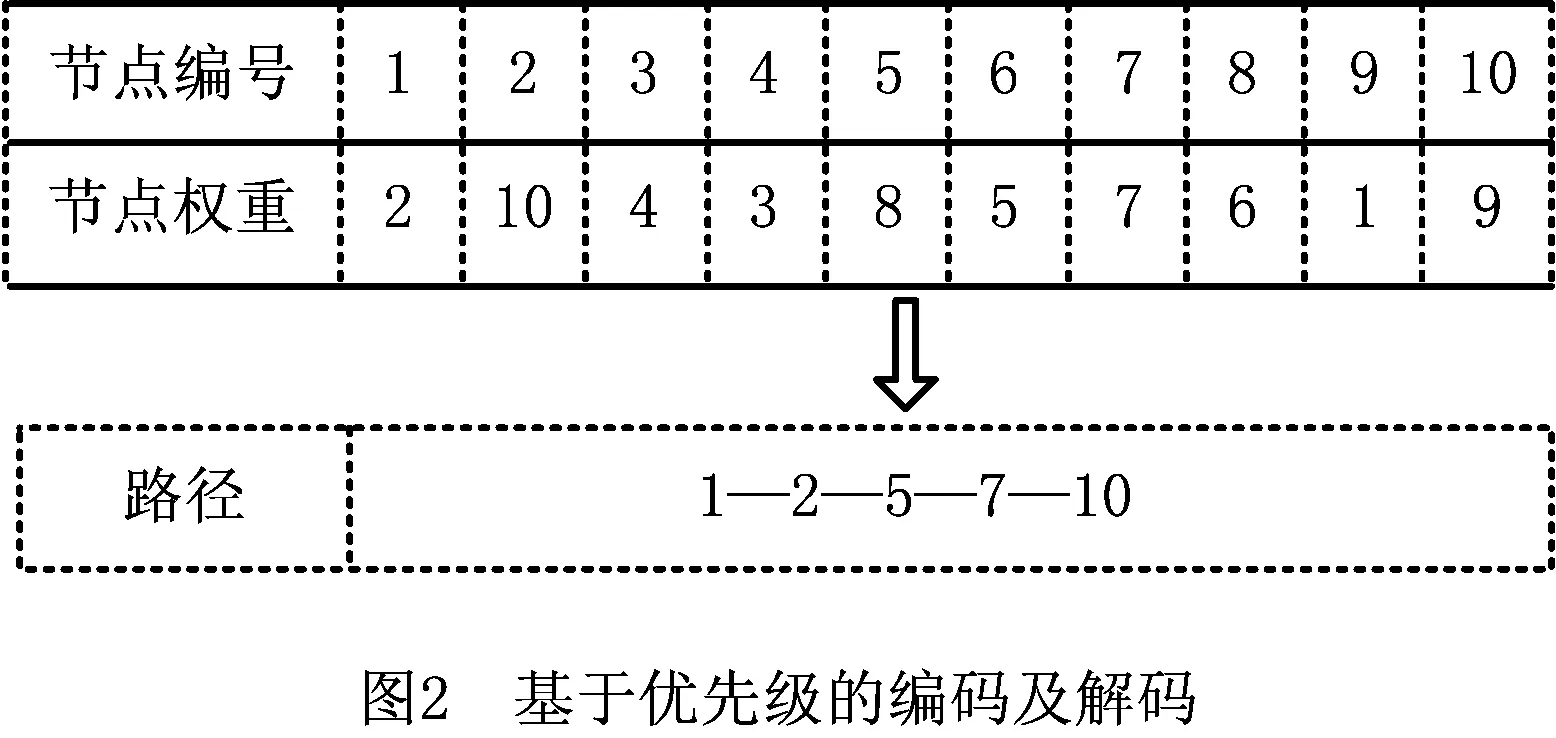
假设存在10个节点构成的无向网络图如图1所示,则编码解码流程如图2所示,可以看出节点1与2,3,4相连,其中权重最大的点为2,则选择路径1—2,以此类推,所选节点在图2中加粗表示,则得到路径1—2—5—7—10。
2.2 粒子群算法的改进
(1)自适应惯性权重
粒子群算法的参数改进中,惯性权重尤为重要,它影响着粒子的移动速度,通过改进惯性权重可以优化粒子群算法搜索最优解的能力,提高了算法的性能。本文采用典型线性递减策略[22],惯性权重ω=ωmax-Iter×(ωmax-ωmin)/Itermax,ωmax,ωmin为粒子惯性权重的最大值及最小值,Iter为当前迭代次数,Itermax为最大迭代次数。
(2)混合遗传算法的交叉变异操作
粒子群算法虽然具有效率高、收敛快速、操作简单等优点,但是存在着早熟的问题,容易陷入局部解。为改进算法,本文将遗传算法中的选择交叉变异操作[23]引入粒子群算法中,以解决早熟的问题。在粒子群算法进行速度和位置更新后计算Pareto解集,选择Paerto解集中拥挤距离较小的点作为指导粒子,以每个粒子与指导粒子的位置向量的差值作为交叉变异的依据,选择差值较小的前20%粒子产生后代粒子取代双亲粒子,并进一步采用变异操作。最后,由于在每个维度上发生交叉变异操作后所得的粒子可能会产生不可行解,对每个维度上的数进行检验,假设存在负数,则将结果修正为随机的正实数。理论上通过引入交叉操作能扩大算法的搜索范围,改善局部搜索能力,同时防止陷入局部最优解,同时在解决多目标问题中,如果存在两个解同时陷入两个不同区域的Pareto解集或局部最优解,则通过该操作扩大搜索范围。其中交叉操作计算公式如下:
child(x)=∂×parent1(x)+(1-∂)parent2(x),
(16)
(17)
式中:child(x)为子代粒子;parent1(x),parent2(x)为父代粒子;∂为0~1之间的随机数。
(3)基于动态拥挤距离的精英解集更新
在构建非劣解集的过程中,保持非劣解集种群的多样性具有非常重要的意义,它可以为决策者提供更多合理的解决方案,本文则采用基于动态拥挤距离的精英解集更新[24]。
拥挤距离是指粒子与其周边粒子之间的拥挤程度,主要用来分析所得Pareto解集的均匀性,在解决多目标问题的过程中,若其含有n个目标函数,分别为f1,f2…fn,则粒子的密集距离U(xi)为:
(18)
式中:xj和xk为在Pareto解集中距离xi最近的两个粒子;fn(xj)为粒子xj在第n个目标函数的值;fnmax为在第n个目标函数的最大值。
通过上述计算,所得的结果便是这个解的拥挤距离(边界解的拥挤距离为无穷大)。拥挤距离越小,则说明所得的解越拥挤,其多样性越小,反之则说明所得的解越分散,其多样性越大。
在算法的迭代过程中,进行拥挤距离的计算后当所得的精英解集的数量T未超过最大容量Tmax时,则继续进行迭代计算;当所得的精英解集的数量T超过最大容量Tmax时,便将所有解的拥挤距离按降序进行排序,删除靠后的Tmax-T个精英解,则剩余精英解集的个数为Tmax。
2.3 算法流程
算法流程如图3所示,具体步骤如下:
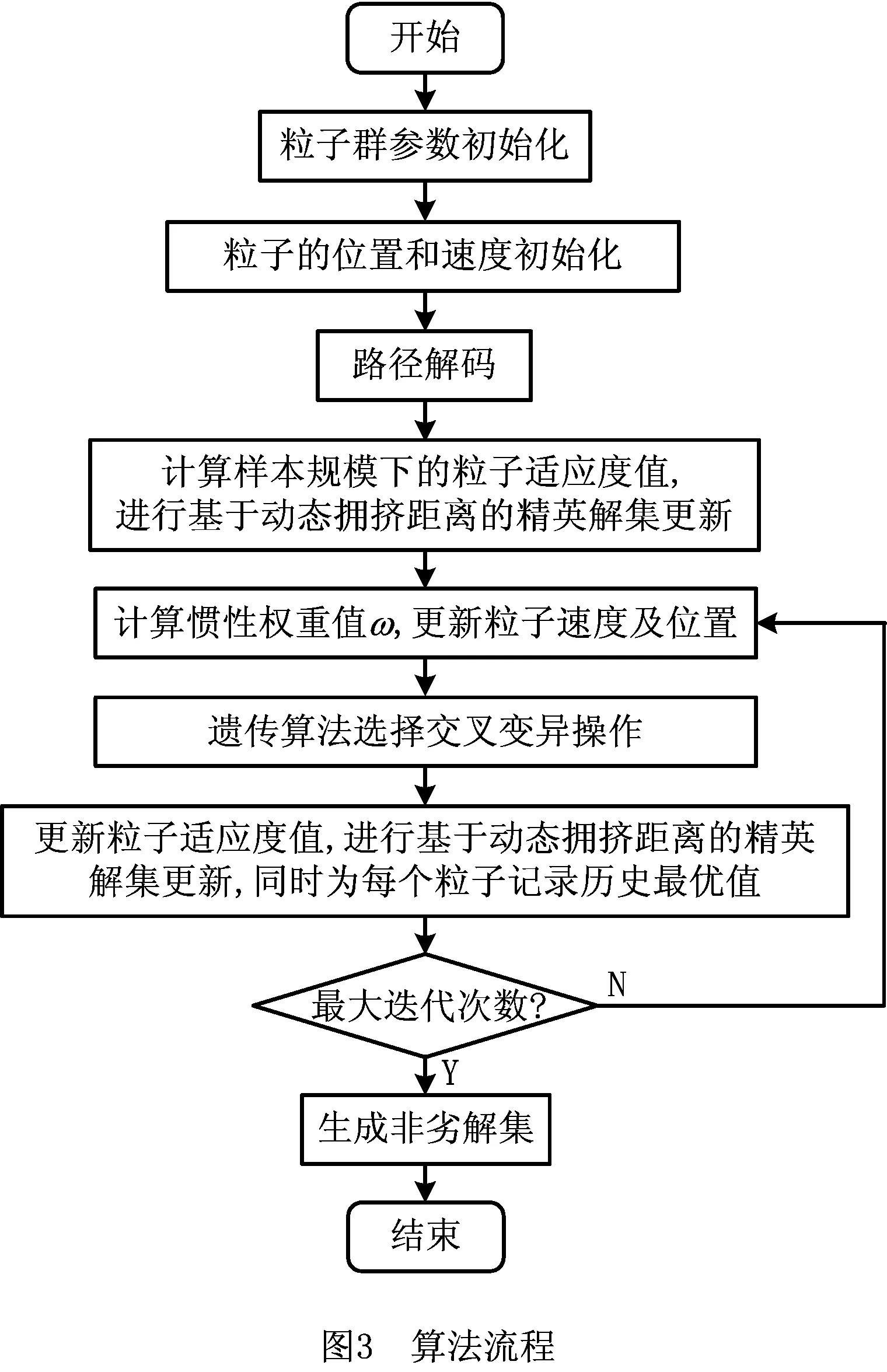
步骤1粒子群算法参数初始化。设定样本规模K,粒子搜索空间维数D,粒子群规模N,学习因子C1、C2,最大迭代次数Itermax,当前迭代次数Iter,最大惯性权重ωmax,最小惯性权重ωmin,惯性权重ω=ωmax-Iter×(ωmax-ωmin)/Itermax,交叉概率Pc,变异概率Pe,交叉池的大小比例Sp。
步骤2路径解码。运用混合多目标粒子群算法求解邻接矩阵得到路径p,计算每个粒子在样本规模下K下的两个适应度值期望Pbest,Qbest,即所选路段的安全系数Zp和成本Cp的期望。对所得适应度值进行评估,当一个粒子不受其他粒子支配(即不存在其他粒子的适应度值Pbest,Qbest期望同时优于该粒子),将粒子存入非劣解集中,得到Pareto解集后进行基于动态拥挤距离的精英解集更新,转步骤3。
步骤3路径更新。根据步骤2所得的Pareto解集,将每个粒子通过根据随机选取一个所构建的Pareto解集中的个体最优粒子位置与自身历史最优位置来更新粒子速度与位置,再进行交叉变异操作,根据交叉概率与交叉池大小比例选取指定数量的粒子放入交叉池之中,池中的粒子随机两两交叉产生相同数目的子代粒子,再根据变异概率进行变异操作,得到新的粒子,转步骤2。
步骤4终止条件。重复步骤2和步骤3,直至迭代次数Itermax。
3 算例分析
3.1 算例
如图4所示为本文构建的无向带权网络图,存在30个节点,90条边和20个人口中心,危险品运输车辆需将危险品m从节点1运输至节点30。算例中路段运输时间、人口中心与周边路段距离、人口
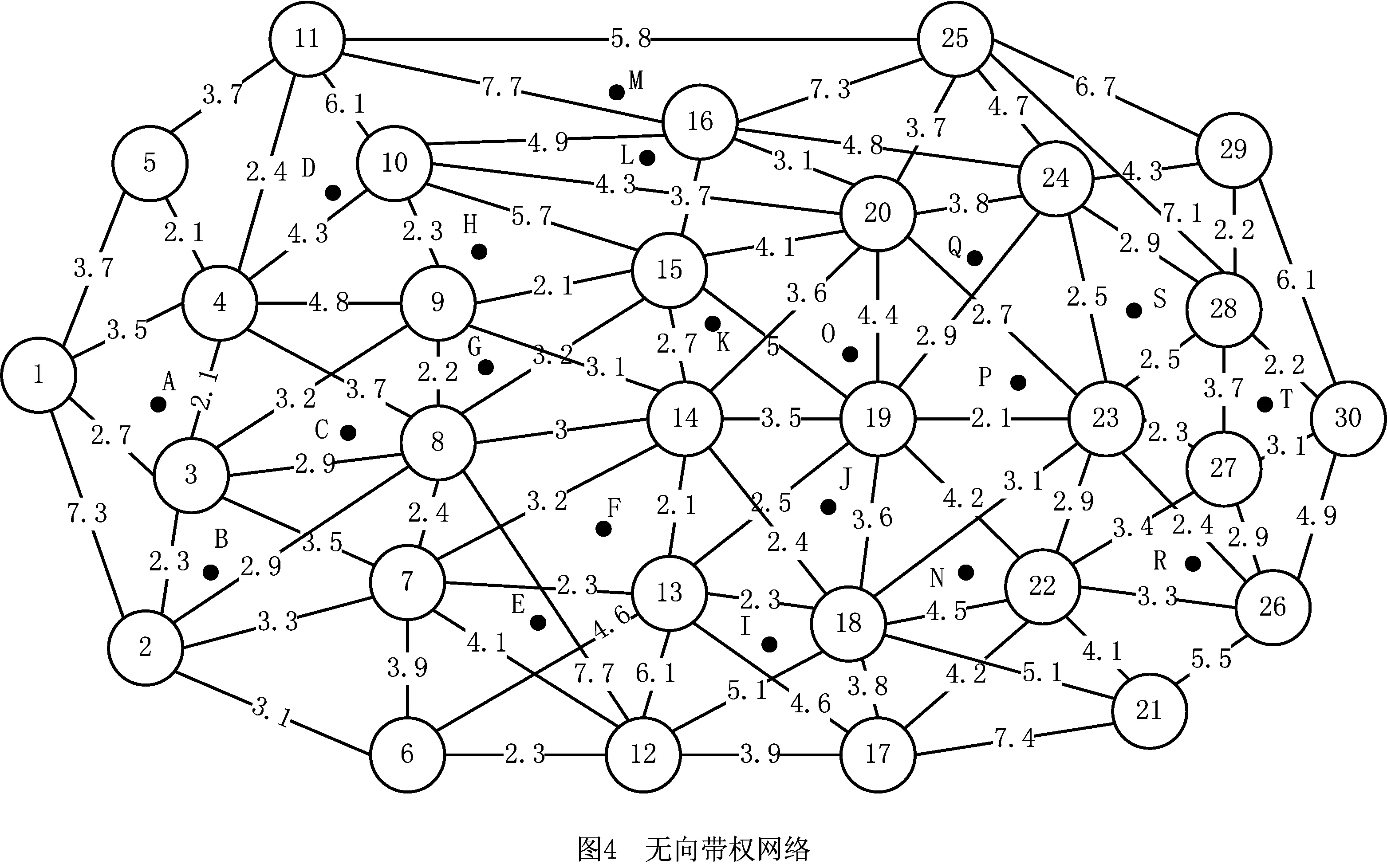
中心数量、终端需求量及种类为随机生成,前两者只生成一次后构建运输网络,图中边上的数字为路段运输时间t∈(2,8),人口中心与周边路段距离如表1所示,由于研究人口中心数量和终端需求量的不确定性,后两者采用样本平均近似法根据样本规模不断生成,人口中心数量W服从正态分布W~N(1500,300),终点需求量Q服从正态分布Q~N(50,10),需求危险品m种类则服从均匀分布随机
整数m∈{1,2,3}。固定参数引用文献[25]对模型的构建,标准安全距离δ=800,即当人口中心到路段的距离大于800时,不考虑危险品运输对人口中心的风险影响,加权因子θ1=0.8,θ2=0.2,最大载货量bmax=80,最小载货量bmin=10,精英解集最大容量Tmax=10。满载量下危险品m在运输产生事故的影响范围γm以及所需成本ηm引用文献[26]如表2所示。
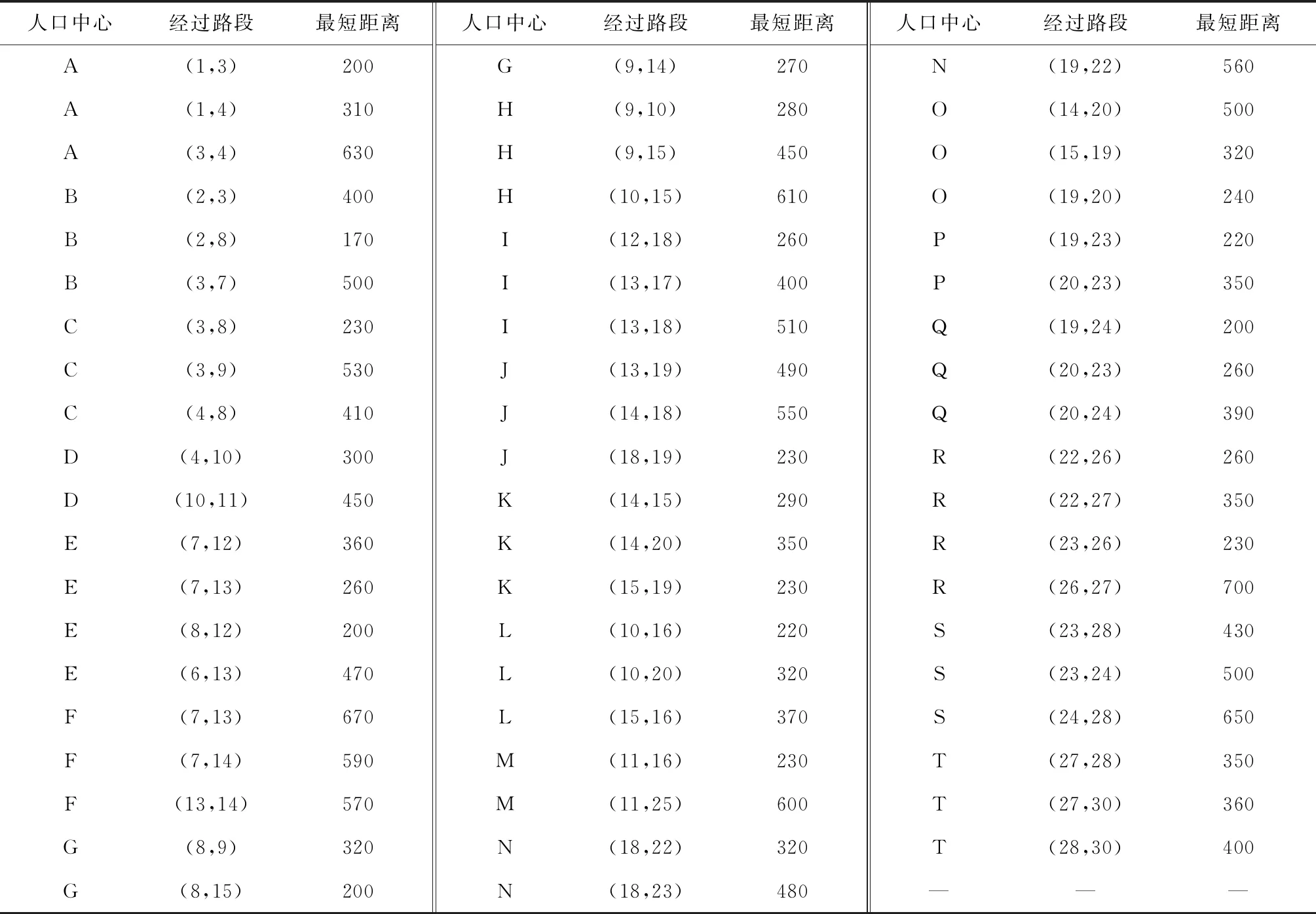
表1 人口中心

表2 危险品信息
3.2 算法参数设置
混合粒子群算法中涉及的参数设置如下:粒子群规模N=1 000,搜索空间维数D=30,最大迭代次数Itermax=400,学习因子C1=C2=2,最大惯性权重ωmax=0.9,最小惯性权重ωmin=0.4,最大退步次数M=4,交叉概率Pc=0.9,变异概率Pe=0.05,交叉池的大小比例Sp=0.2,采用MATLAB软件编码实现上述算法,运行平台为Intel(R)Core(TM)i5-5200U2.20 GHz CPU,4.0 G内存的计算机。
3.3 结果分析
表3为当样本规模为500时,算法得到以最小风险系数期望和最低成本期望为目标的Pareto解集,得出8种路径方案,并计算得出每个方案的风险系数和成本的期望值。其中可以看出方案1的风险系数期望最低,成本期望最高;方案8的风险系数期望最高,成本期望最低。
图5为3种不同算法下对模型求解所得到的Pareto前沿,通过将IMOPSO、带精英策略的非支配排序的遗传算法(fast elitist Non-dominated Sorting Genetic Algorithm, NSGA-Ⅱ)和基于分解的多目标进化算法(Multi-objective Evolutionary Algorithm Based on Decomposition, MOEA/D)[27]对模型进行求解,对比可知IMOPSO所得的Pareto解集更优,且明显看出更为均匀。
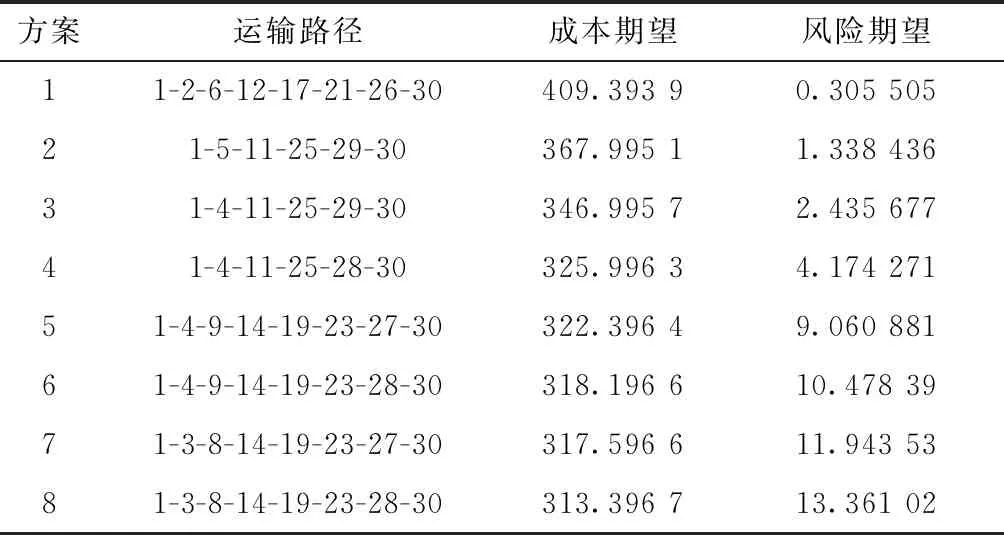
表3 Pareto最优解
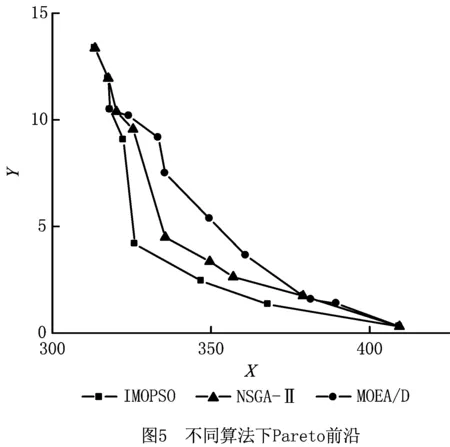
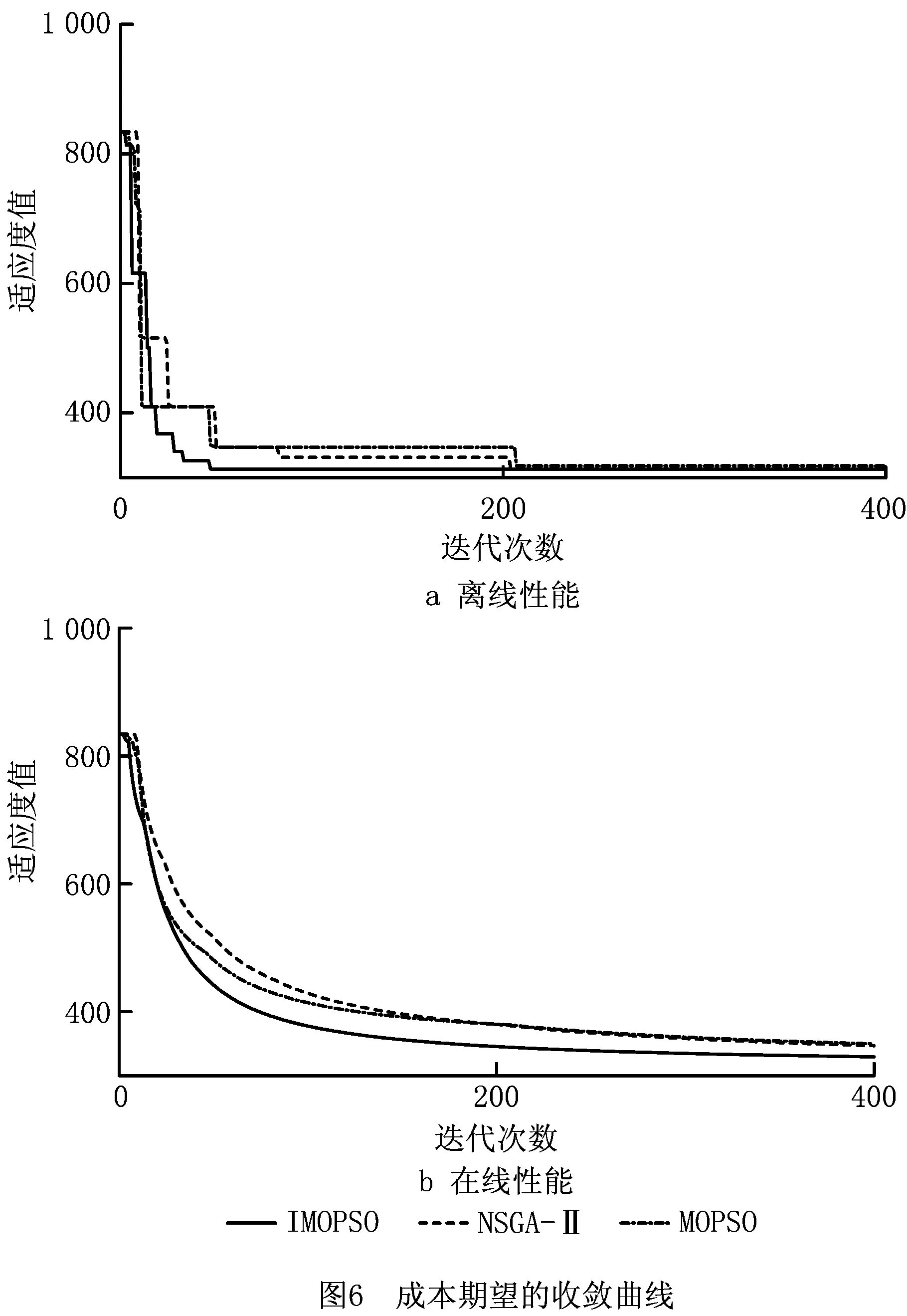
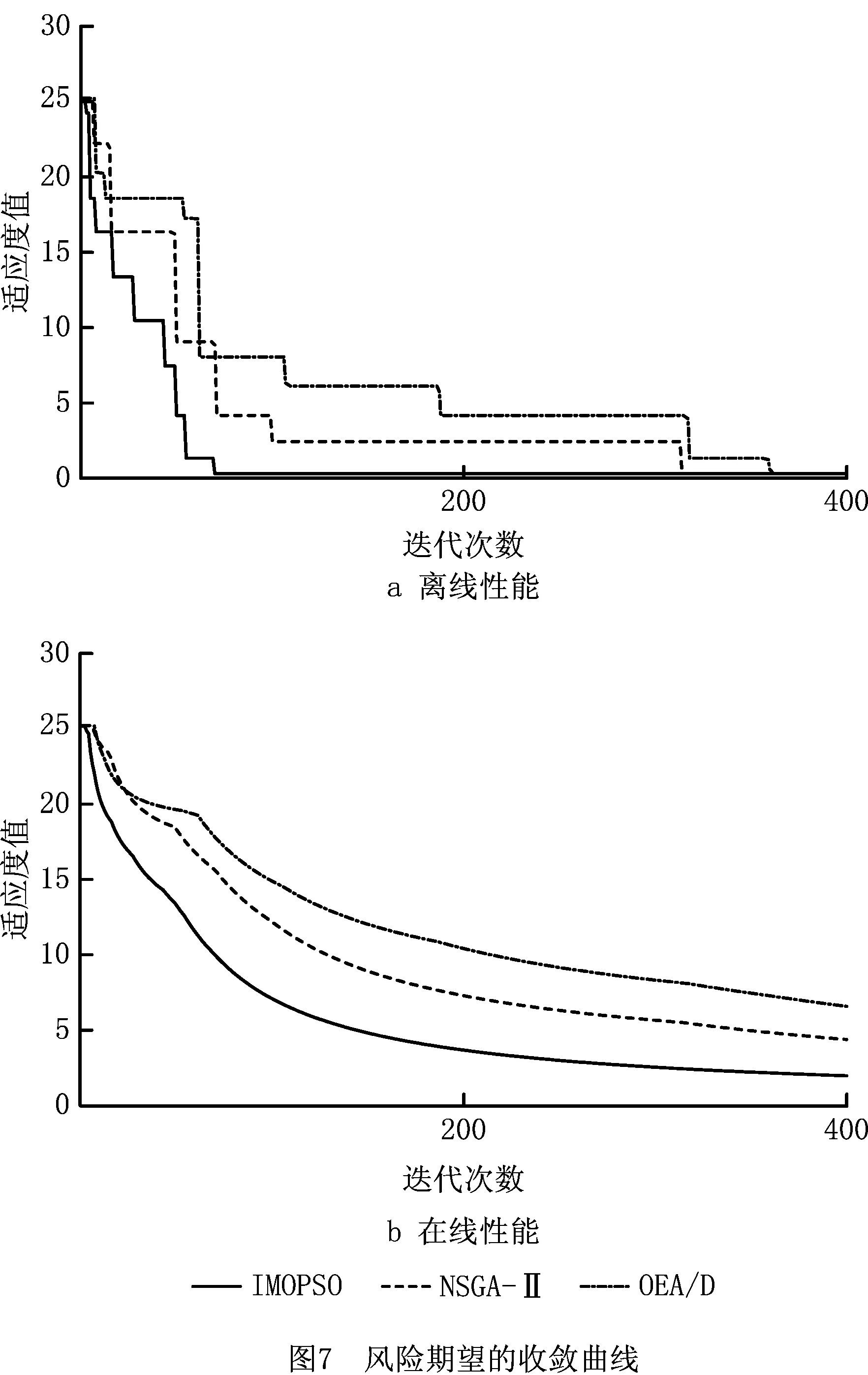
图6和图7为算法迭代性能的对比,外部解[28]是指每次迭代过程之中Pareto解集中某一目标适应度值最优时的解,通过测试两个目标的适应度值在迭代过程中的变化过程,即离线性能和在线性能,可以看出算法在迭代过程中的收敛性。可以看出,IMOPSO具有更好的收敛性,能够快速地找到外部解,具有更好的效率。
在危险品运输路径规划中,由于其特殊性在规划后不会轻易改变,应进一步考虑危险品运输的稳定性,人口和需求量的不确定性则会对路段的稳定性造成影响,进而扩大危险品运输事故的造成的影响。图8表示在样本规模从100~1 000时对于Pareto解集中成本和风险两个目标的期望曲线图,当样本规模超过300后所得的Pareto解集中的方案期望均逐渐趋于稳定,说明算法所得的优化方案具有一定的稳定性和可靠性;由表4可知,从成本和风险两个目标期望值在样本规模下所得的方差可以看出,成本期望越高,或是风险期望越高,相对应的所得的方差也越高,受人口数量和需求不确定性影响
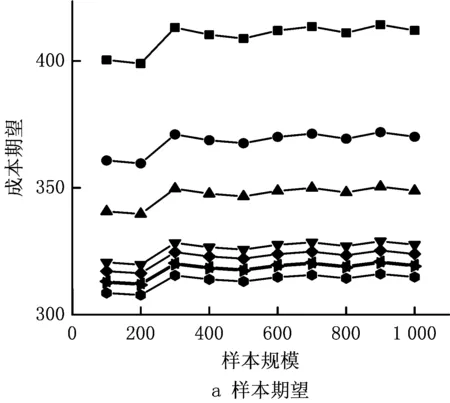
越大,则该路段稳定性较差。比如方案1和方案2的成本方差较高,而风险方差较低,则说明方案1和方案2的路径中人口数量和需求不确定性对成本影响较大,而对风险影响较低。
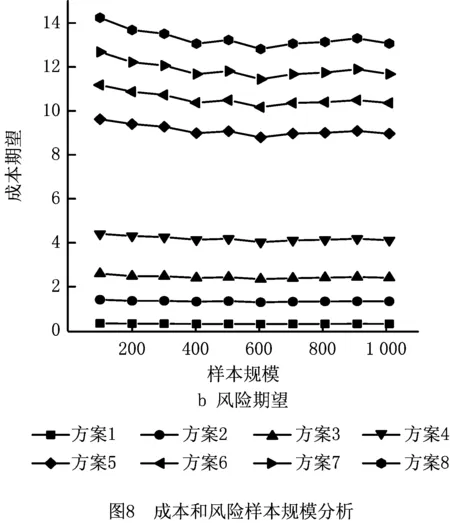

表4 样本规模方差
3.4 灵敏度分析
为进一步研究人口中心数量和终端需求量对所选路径的运输风险和成本的影响,在保持样本规模为500,其他条件不变的前提下,分别对集中人口数量和终端需求量进行灵敏度分析。
图9为在人口中心期望变化下所得的Pareto解集,集中人口中心期望服从正态分布,方差σ2为400,其期望值μ以1 100为起点,以200的步长,变化至1 900。由图8可知,Pareto曲线随着人口中心期望的变化均匀上升。同时,人口中心期望主要对风险期望产生影响,当Pareto解集中所选方案的风险期望越高,随着人口中心期望的增加变化率也越高,则说明所选方案受人口中心的影响越大。可以看出,方案1~方案4受人口中心期望数量影响明显,这些路线靠近运输网络中人口中心区域。
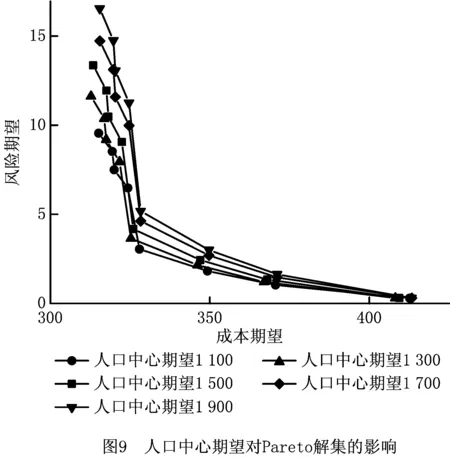
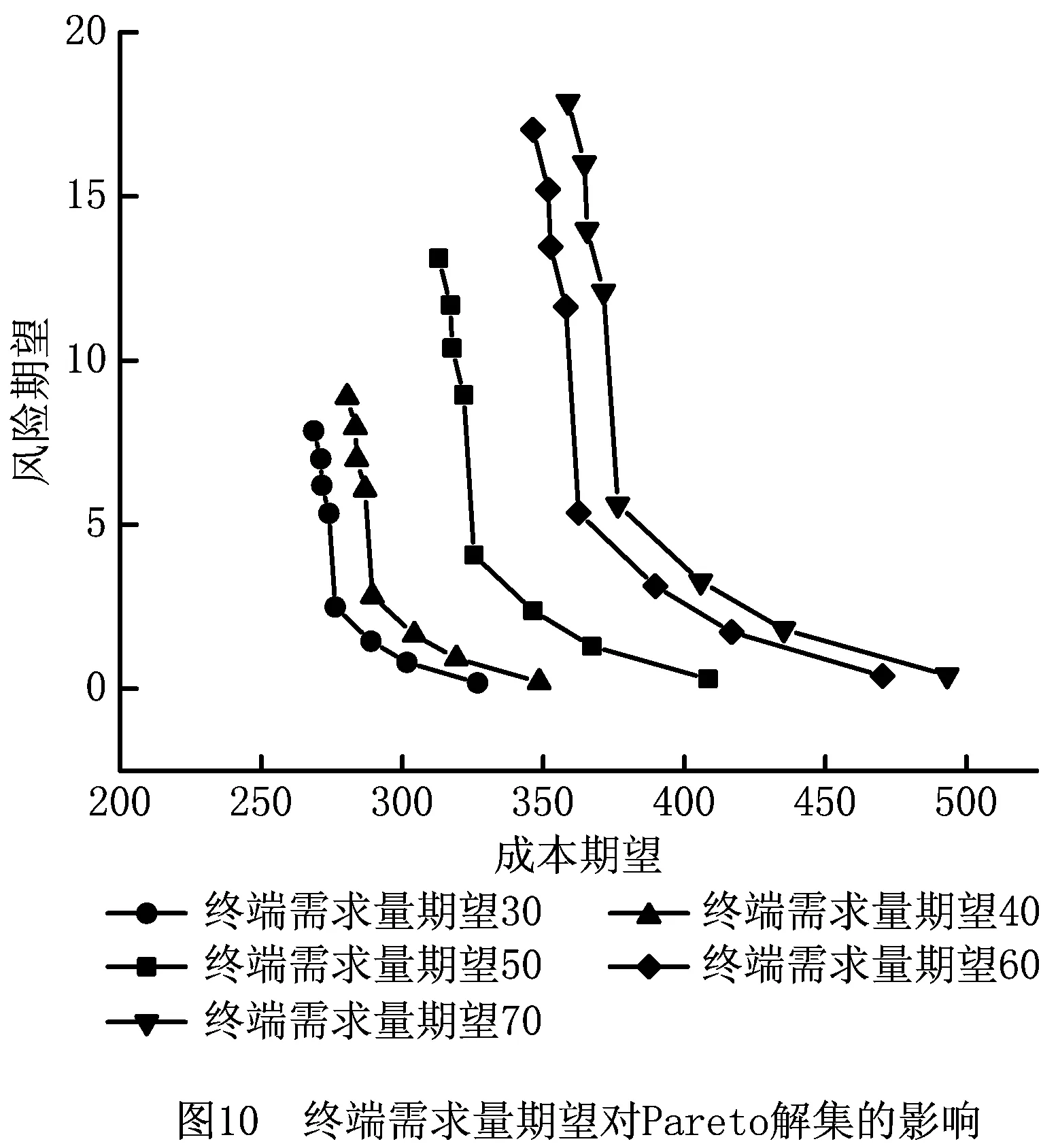
图10为在终端需求量变化下所得的Pareto解集,终端需求量服从正态分布,方差σ2为10,其期望值μ以30为起点,以10为步长,变化至70。经重新计算可以看出终端需求量在40~60时,存在明显的Pareto改进,当终端需求量低于40或超过60时,变化趋势将不再明显,并将趋向于一定的值。可以看出终端需求量对风险期望和成本期望均有一定影响,且在Pareto曲线中,Pareto解集中的单目标的值越大,产生的变化越大。
3.5 算例结果分析
综上所述,根据对算例结果的分析可以看出,方案1和方案2的运输成本较高,风险较低,所选路段运输时间较长,尽可能避开人口中心区域,通过样本规模分析及灵敏度分析得出方案1和方案2的成本受不确定条件影响较大,其风险性受不确定条件影响较小,因此当需求为危险级别较高的危险品时决策者可以选择方案1和方案2。方案5~方案8的运输成本较低,风险较高,所选路段运输时间尽可能短,其经过部分人口集中路段,通过样本规模分析及灵敏度分析得出方案7和方案8的风险性受不确定条件影响较大,其成本受不确定条件影响较小,则当需求为危险级别较低的危险品时决策者可以选择方案7和方案8。方案3和方案4的成本和风险性相比结果中其他方案处于中等水平,所选路段运输时间其经过较少的人口集中路段,两者稳定性均相对较好,因此当需求存在多种危险级别的危险品或是危险级别中等的危险品时决策者可以选择方案3和方案4。
4 结束语
本文以危险品运输路径优化为研究对象,构建了以最低运输风险、最低运输成本为目标的双目标优化模型,并在此基础上以危险品需求量和集中人口数量为随机变量,构建了双重不确定条件下的随机优化模型;结合Pareto理论和混合多目标粒子群算法对提出的模型进行求解,并对模型和算法进行算例分析。
算例实验结果表明:①验证了所提出的随机优化模型和算法的有效性,混合多目标粒子群算法可以有效求解多目标随机优化模型,得出Pareto解集并计算运输路径的稳定性,为决策者根据实际情况,考虑路线的风险、成本、稳定性等综合因素所进行的路径决策提供支持。②通过算法的对比,测试不同算法得到的Pareto解集以及迭代过程中的适应度值的变化,得出结合自适应惯性权重和遗传算法中交叉操作的混合多目标粒子群算法具有更好的收敛性、挖掘性和活动性,能快速寻找非劣解集并向其收敛的同时部分粒子仍在外部活动,防止算法陷入局部最优解。③通过对不同样本规模的稳定性分析得出所得方案稳定性均相对较好,进一步对两个不确定条件进行灵敏度分析,结果表明人口中心主要对危险品风险期望具有影响,且风险期望越高,受到人口中心影响越大;终端需求量对危险品运输风险期望和成本期望均有影响,且接近一定范围时变化趋势变小,说明根据客户终端需求量可以对车辆的选择进行进一步考虑,控制Pareto解集的范围,控制运输路径的成本和风险。
本文仍存在一些不足,如在模型建立的过程中,只考虑到起点到终点的危险品运输路径优化,并未考虑时变条件对危险品运输路径优化的影响。在今后的研究内中,将考虑如何将算法运用于带时间窗的危险品运输轴幅式网络优化问题。
