基于师生交流机制的改进类电磁机制算法
2020-05-08徐惟罡张春江
吴 擎,徐惟罡,张春江
(1.华中农业大学 工学院,湖北 武汉 430070; 2.华中农业大学 农业部长江中下游农业装备重点实验室,湖北 武汉 430070; 3.华中科技大学 数字制造装备与技术国家重点实验室,湖北 武汉 430074)
0 引言
很多实际的优化问题都需要满足一定的约束条件,因而约束优化问题具有非常广泛的工程应用背景,即很多工程应用问题可归纳为约束优化问题。这类问题通常有几大特点:非凸、不可微、存在多个局部极值等。传统的优化方法在解决这类问题时往往会失效,或者花费较长的计算时间。而近年发展起来的元启发式算法,如粒子群优化(Particle Swarm Optimization, PSO)算法[1]、布谷鸟算法(Cuckoo Search, CS)[2]、蜻蜓算法(Dragonfly Algorithm, DA)[3]等,不要求解的绝对精确性,在合理的计算时间内,能够有效求得问题的最优解或近优解,同时算法还具有良好的普适性等优点,因此元启发式算法得到了广泛关注与研究。
类电磁机制(Electromagnetism-like Mechanism, EM)算法是由Birbil等[4]于2003年提出的一种元启发式算法,算法通过模拟电磁场中粒子的吸引排斥实现寻优功能。EM算法具有原理简单、全局搜索能力强等优点,并应用在各类工程优化问题中[5-9]。随着EM算法的广泛应用,其性能上的不足也展现出来。为提高EM算法的性能,姜建国等[10]利用佳点集理论改进了算法的初始化过程;Rocha等[11]结合Hooke-Jeeves的模式搜索方法,对算法的移动公式进行了改进;韩丽霞等[12]在粒子移动的过程中引入扰动项,在一定程度上解决了算法早熟收敛问题;Lee等[13]采用PSO算法取代EM算法中的随机局部搜索,提高了算法的局部搜索能力;Feng等[14]利用一种改进的Davidon-Fletcher-Powell算法对EM算法的优化结果进行二次优化,改进了算法的整体搜索结果。上述这些改进虽然在一定程度上可以提升EM算法的性能,但在求解一些复杂度较高的问题时,算法的寻优精度和稳定性仍有待提高,同时如何更好地将算法用于解决实际的工程约束优化问题还有待更深入的研究。
因此,本文提出一种求解约束优化问题的基于师生交流机制的改进类电磁机制(Teaching-Learning based Electromagnetism-like Mechanism, TLEM)算法。该算法将教学优化算法和一种改进的类电磁机制算法相结合,不仅保留了EM算法优良的全局寻优能力,还提高了算法的局部寻优精度。为了验证改进算法的性能,本文采用13个标准测试函数对TLEM算法进行测试,并与若干其他约束优化算法进行对比,结果表明改进的新算法具有更好的寻优精度和稳定性。最后,将TLEM算法应用到压力容器、压缩弹簧及焊接梁设计优化问题的求解中,均取得了较好的优化效果。
1 基于师生交流机制的改进类电磁机制算法
1.1 改进的EM算法(IEM)
1.1.1 EM算法简介
EM算法将种群中的粒子类比为电磁场中的带电粒子,粒子间会产生相互作用力,在力的作用下粒子产生移动,最终移动至较优区域。算法主要包括初始化、局部寻优、计算合力以及移动粒子4个步骤,具体如下[4]:
步骤1初始化种群。在搜索空间内随机生成m个粒子作为初始种群,计算每个粒子的适应度值f(Xi),找到并标记适应度值最优的粒子为Xbest。
步骤2局部寻优。对种群中的当前最优粒子Xbest进行局部搜索。
步骤3计算合力。粒子所受力的大小以及性质(吸引力或排斥力)均取决于粒子的电量。粒子i的电量qi及合力Fi计算公式如下:
(1)
(2)
步骤4移动粒子。计算合力之后对粒子进行移动,形成新一代种群。移动的方向和步长按式(3)计算:
(3)
式中:λ为0~1的随机数,RNG为上下界内可移动的范围。
1.1.2 IEM算法
在原始EM算法中,一个粒子的合力由M-1个粒子计算得出,即在每一次迭代中需要进行(M-1)2次计算,这会耗费大量的计算时间。尤其当M越大时,计算时间会剧烈增加。因此计算合力时,随机从M-1个粒子中挑选出3个粒子计算合力。这样不仅可以减少计算时间,还可以避免过多合力一起计算时相互抵消。除此以外,Gao等[15]发现移除合力计算公式中的欧式距离可以让粒子的移动步长变大,避免粒子陷入局部极值。综上所述,合力计算公式改进为:
(4)
式中R1,R2,R3表示除粒子i外随机从剩下的M-1个粒子中挑选出的3个粒子。
Rao等[16]通过引入移动概率MP对移动公式进行修正。具体方式为:如果在某一维度,随机数小于MP,则使用改进后的移动公式,否则使用原始的移动公式;若使用改进后的移动公式使粒子超出边界,则仍使用原移动公式;若移动后粒子的适应度大于原始位置,保留原始位置,否则接受新的位置。综上,移动公式更改为:
(5)
(6)
其中参数λ和Rand为0~1的随机数。
1.2 教学优化算法
教学优化算法(Teaching-Learning-Based Optimization, TLBO)将种群类比为一群学生,决策变量类比为学习科目,适应度值代表学生的成绩,种群中的最优解则被看作教师。算法包括“教师阶段”(teacher phase)和“学生阶段”(learner phase)两个部分[16]。
在教师阶段,通过让学生整体水平平均值(M)向教师水平靠拢的方式跟随教师进行学习,具体形式如下:
Difference_Meani=ri(Mnew-TFMi),
(7)
Xnew,i=Xold,i+Difference_Meani。
(8)
其中:Mnew为第i代教师的变量值,Mi为第i代学生的平均变量值,TF为1或2的随机数,ri为0~1的随机数。
在学生阶段,学生通过随机选择另一名学生交流的方式进行学习,具体形式如下:
i≠j。
(9)
其中Xi、Xj分别代表第i代的两名不同学生。若新解Xnew比旧解Xold好,则接受新解,否则维持旧解。
1.3 约束处理规则
对于无约束优化问题,粒子的适应度值越小,则粒子越优。但对于约束优化问题,粒子的好坏不仅和适应度值相关,还与约束违反量有关。约束违反量φ(X)定义如下:
(10)
式中:gi(X)代表不等式约束,hj(X)代表等式约束。从式(10)可以总结出:当粒子是可行解时,φ(X)的值永远为0;当粒子为非可行解时,φ(X)>0;违反的约束越多,φ(X)的值越大。
本文利用Deb[17]提出的可行域与支配规则来处理约束,具体规则为:若两个解都违反约束条件,则具有较小约束违反量的解优于另一个解;若一个解满足约束条件,另一个违反约束条件,则满足约束条件的解较优;如果两个解都满足约束条件,则具有较小适应度值的解更优。
同时,对于约束优化问题,粒子的电量也应与其约束违反量相关。因此电量计算公式修正为:
(11)
(12)
从式(11)和式(12)可以看出,可行解的电量大于不可行解的电量,约束违反量小的解,其电量大于约束违反量大的解。
1.4 TLEM算法
结合TLBO算法快速收敛特性和IEM算法良好的全局搜索性能,本文提出TLEM算法。算法主要分为两部分:①使用TLBO算法提高种群的收敛速度;②使用IEM算法进行种群寻优。TLEM算法的基本流程图如图1所示。
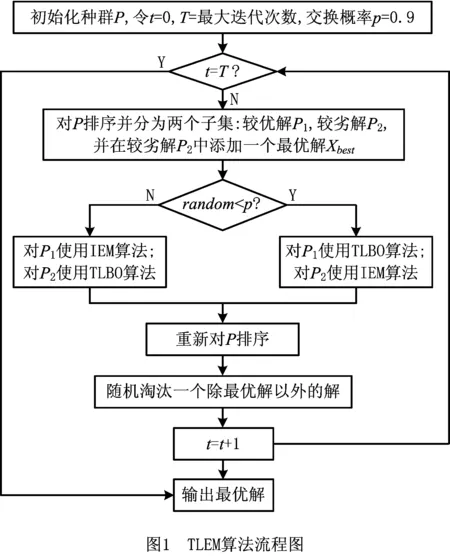
根据流程图,TLEM算法的主要步骤如下:
步骤1初始化种群P,计算所有解的适应度,保留当前种群最优解Xbest。
步骤2结合解的适应度值及约束处理规则,对P中所有解排序,然后平均分为两个解集—较优解P1和较劣解P2,并在P2中添加一个最优解Xbest。
步骤3判断随机数random是否小于p,若是,
则对P1执行TLBO算法,对P2执行IEM算法,否则对P1执行IEM算法,对P2执行TLBO算法。
步骤4重新对P中所有解排序。
步骤5随机淘汰P中一个除最优解以外的解,迭代次数加一。
步骤6判断算法是否满足终止条件,若满足则输出最优解,否则返回步骤2。
2 数值仿真及分析
2.1 仿真实验设计
为检验算法的有效性,将TLEM算法与4个版本的EM算法(CEM、PEM、FADEM、SAPEM)[18-21]分别对13个标准测试函数(G01,G02,…,G13)进行测试,测试结果以平均值、标准差、最优值和最差值作为评价标准。13个测试函数的相关性质如表1所示[22],其中G02、G03、G08以及G12为求最大值问题,其余均为求最小值问题。
算法的相关参数设置如下:种群大小为100,移动概率MP=0.9,交换概率p=0.9,函数评价次数为350 000次。等式约束条件h(X)=0转化为不等式约束|h(X)|-ε≤0(ε=10-4);求最大值问题转化为求最小值问题。
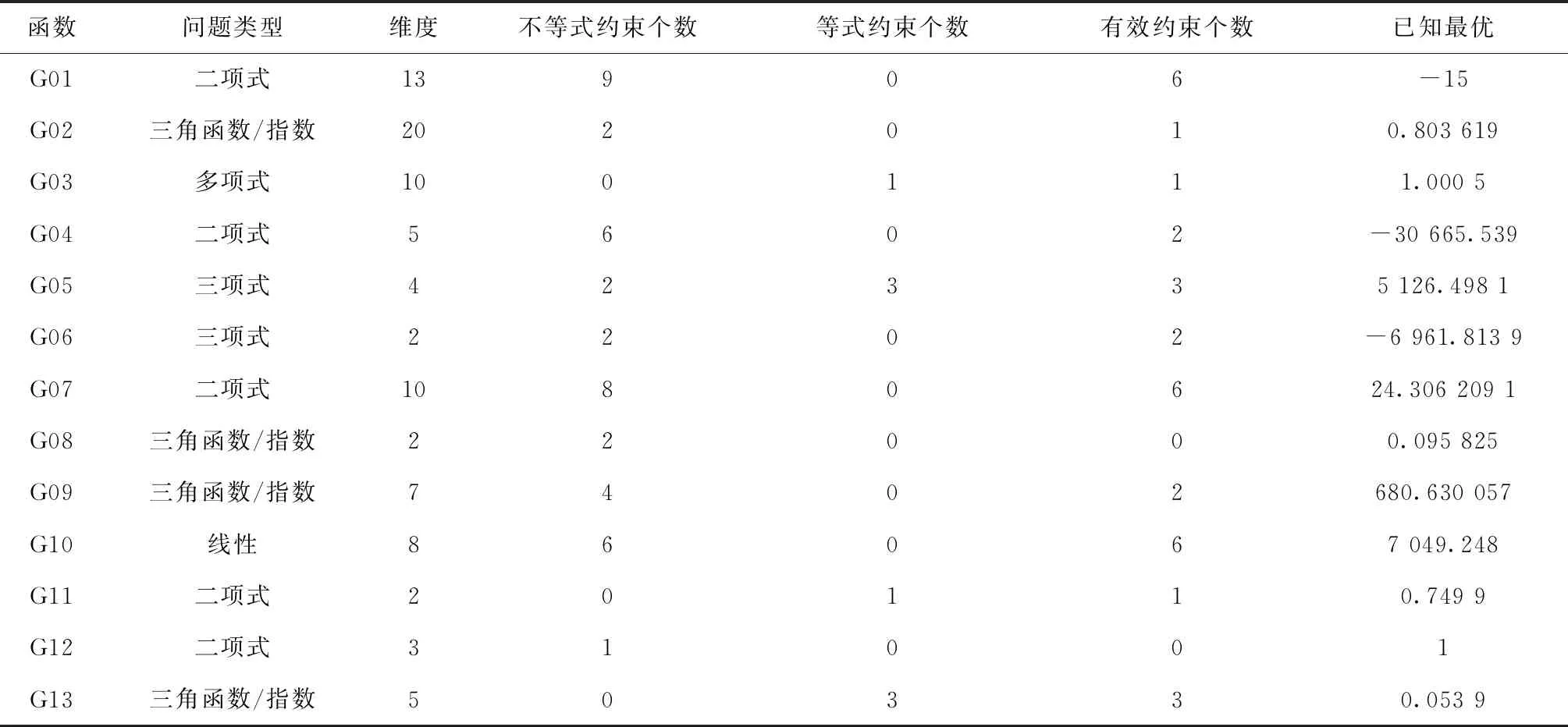
表1 13个标准测试函数
2.2 仿真结果及分析
TLEM算法对标准测试函数的优化结果统计如表2所示。从表2可以看出,TLEM算法几乎在所有的测试函数上都搜索到了最优解,同时除了G11和G13以外,其平均值和最差值都非常接近最优值,13个测试函数中有7个函数的标准差等于0,这说明TLEM算法不但对约束优化问题具有较强的全局搜索能力,而且还具有很强的稳定性。
TLEM算法与其他EM算法在最优值、平均值和最差值上的比较结果分别如表3~表5所示。从表3可以看出,除了函数G03是FADEM算法取得最优,G05、G11是PEM算法取得最优,TLEM算法在其他10个函数上的优化结果均优于其他算法,这表明TLEM算法在搜索性能上较其他版本EM算法有很大的提高,同时也从侧面证明,算法中引入TLBO算法提高了算法的局部搜索精度。从表4可以和表5可以看出,在平均值上,除了G02、G03、G11、G13分别为SAPEM、CEM、PEM和CEM算法取得最好值之外,TLEM算法在其余9个函数上都取得了最好值;在最差值上,除了G03、G11、G13为CEM算法取得最好值之外,TLEM算法在其余10个函数上都取得了最好值。也就是说TLEM算法在求解平均值以及最差值时,绝大部分函数的优化结果均优于其他版本的EM算法,这表明TLEM算法在全局搜索能力和算法稳定性上皆优于其他版本EM算法。综上所述,TLEM算法的综合性能优于其他4个版本的EM算法,说明对于EM算法的改进是有效的。
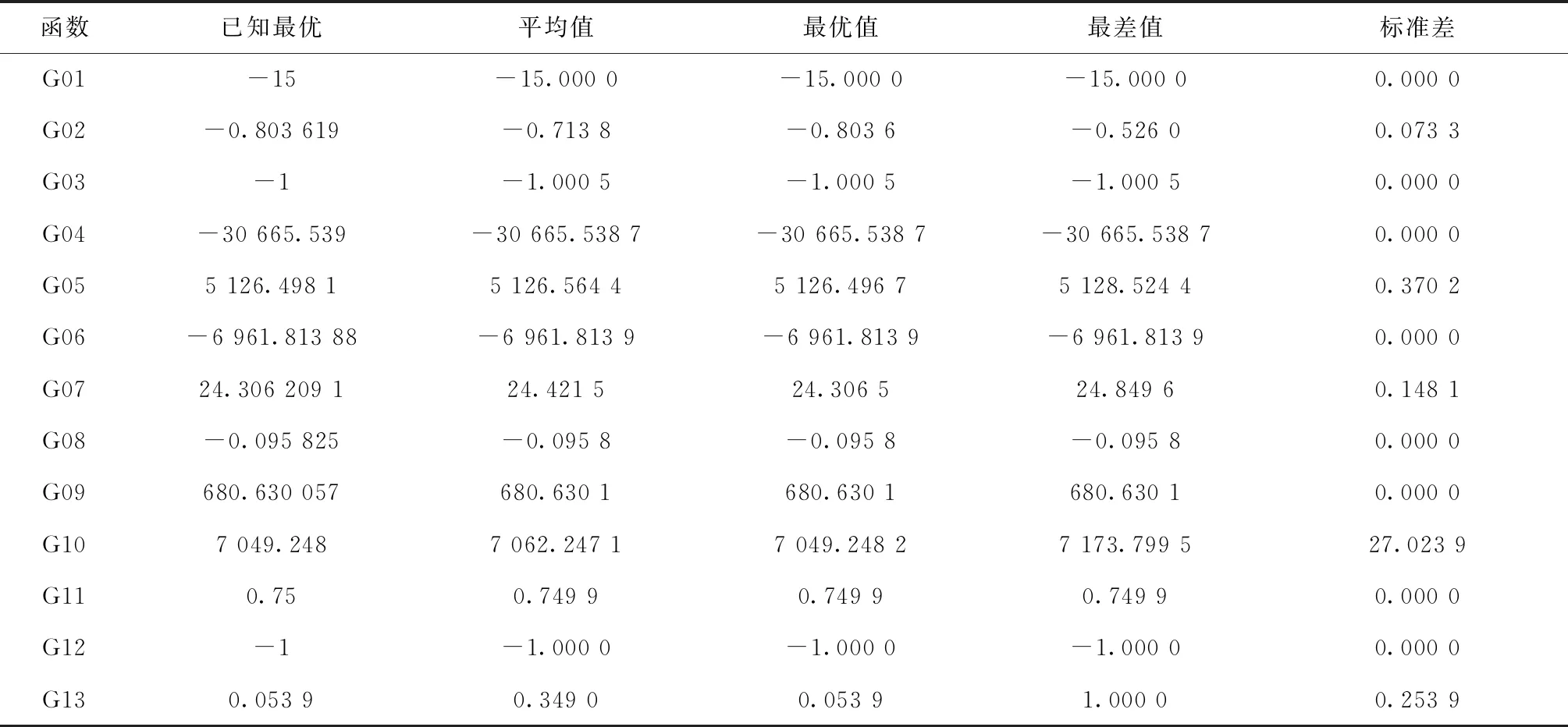
表2 TLEM算法在13个测试问题上的结果
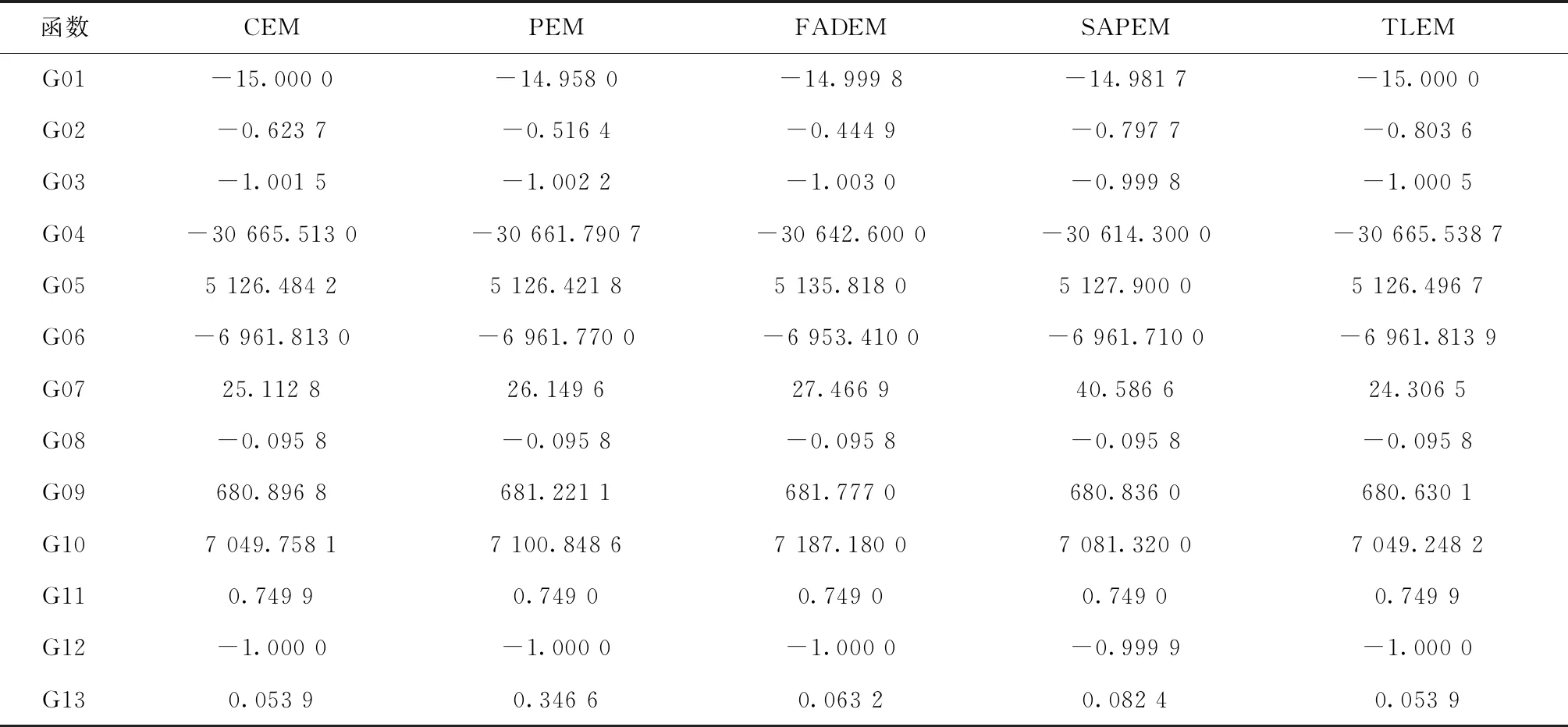
表3 TLEM算法与其他EM算法在最优值上的比较
为了进一步检验算法的有效性,将TLEM算法与若干个新型约束优化算法(PSO+、RGenIII、Gen.V、Rgen.V、eABC、FA)[1]进行对比,算法测试结果以最优值、最差值和平均值作为评价标准,比较结果如表6所示。从表6可以看出,TLEM算法在绝大多数测试函数的各项指标上,较之其他几个算法都要更优。具体地,在函数G01、G03~G12上,TLEM算法在最优值、最差值和平均值上都取得了最好结果,尤其是在函数G05、G07和G10上,其他几个算法的最优值和最差值相差较大,而TLEM在求解这3个函数时最优值和最差值相差不大,说明TLEM算法具有更好的稳定性。在函数G02和G13上,TLEM能够取得最好的最优值,在最差值和平均值这两个指标上稍差一点。综上所述,TLEM算法是一种很有竞争力的约束优化方法。
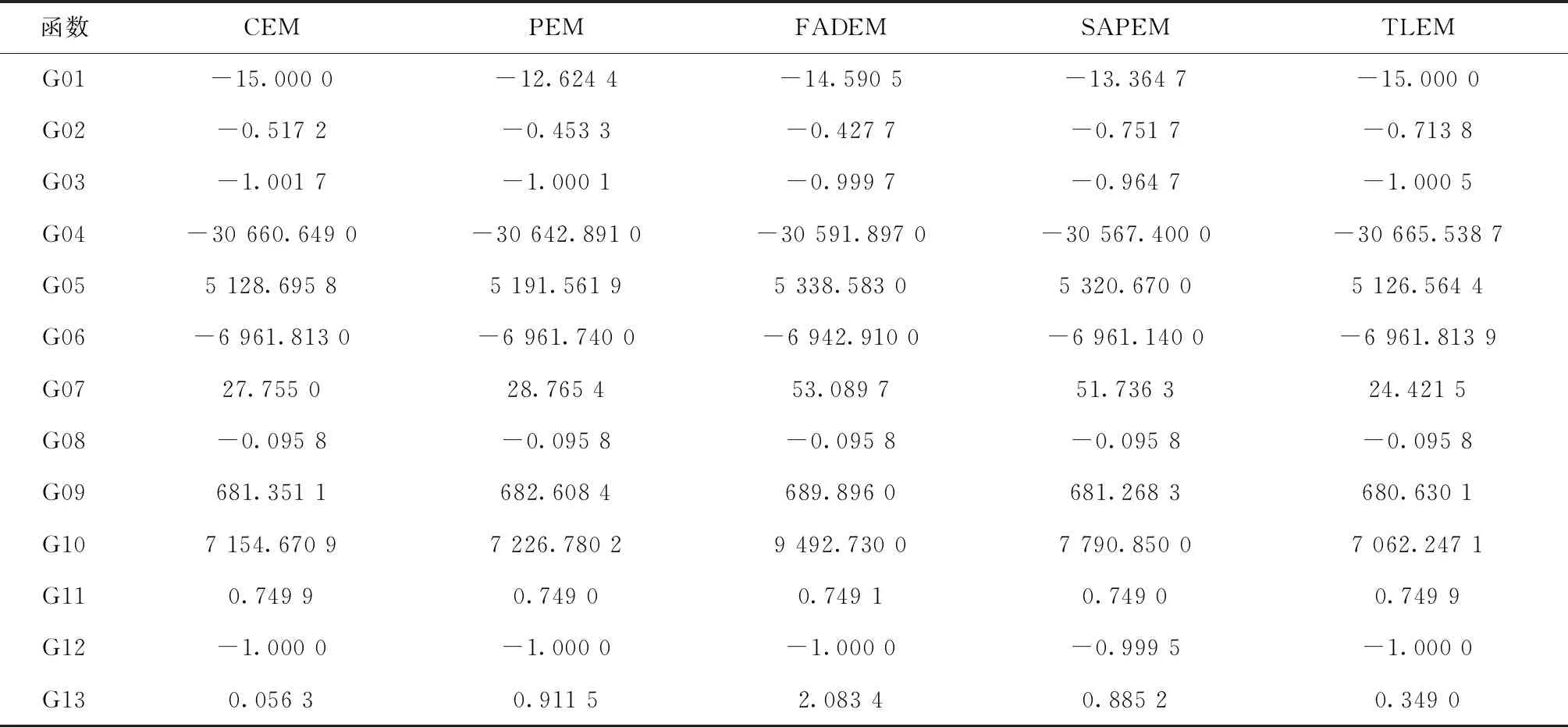
表4 TLEM与其他EM算法在平均值上的比较
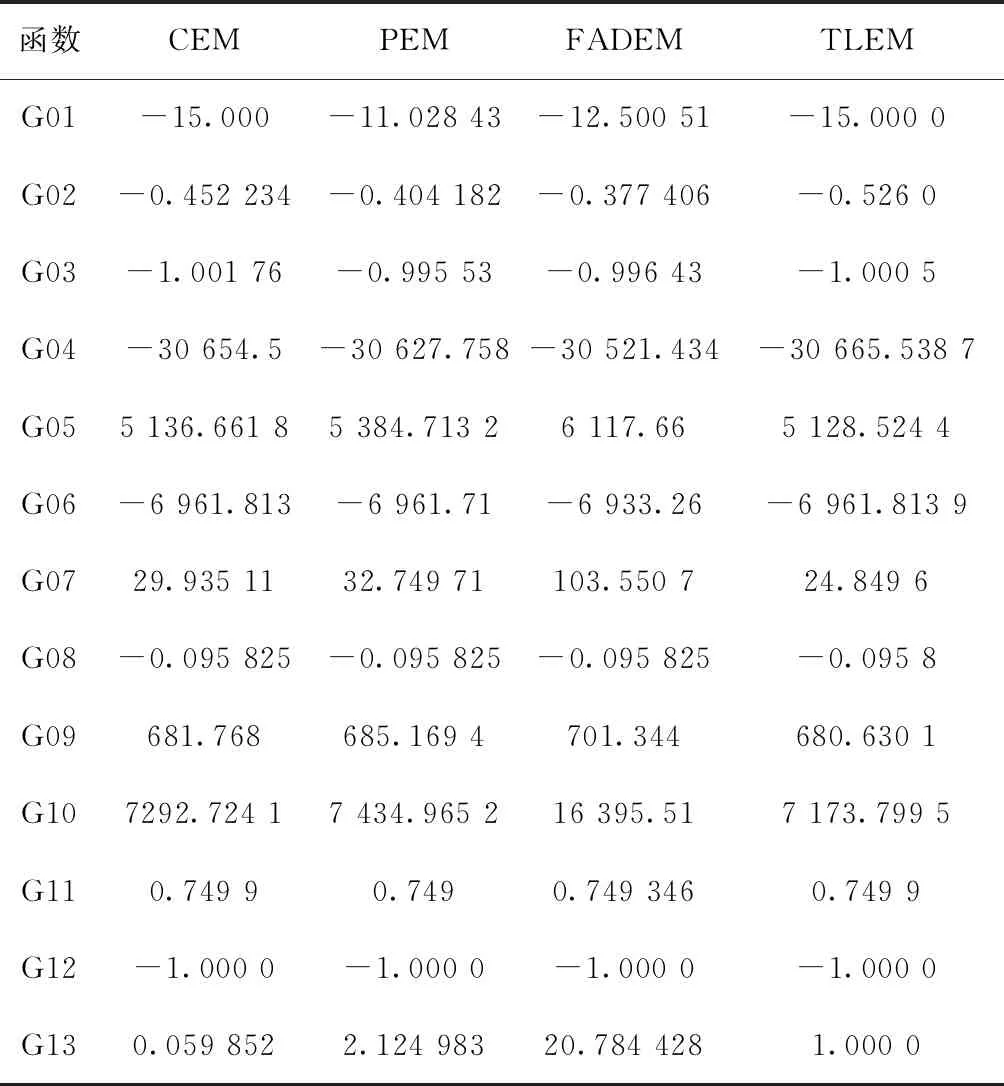
表5 TLEM与其他EM算法在最差值上的比较
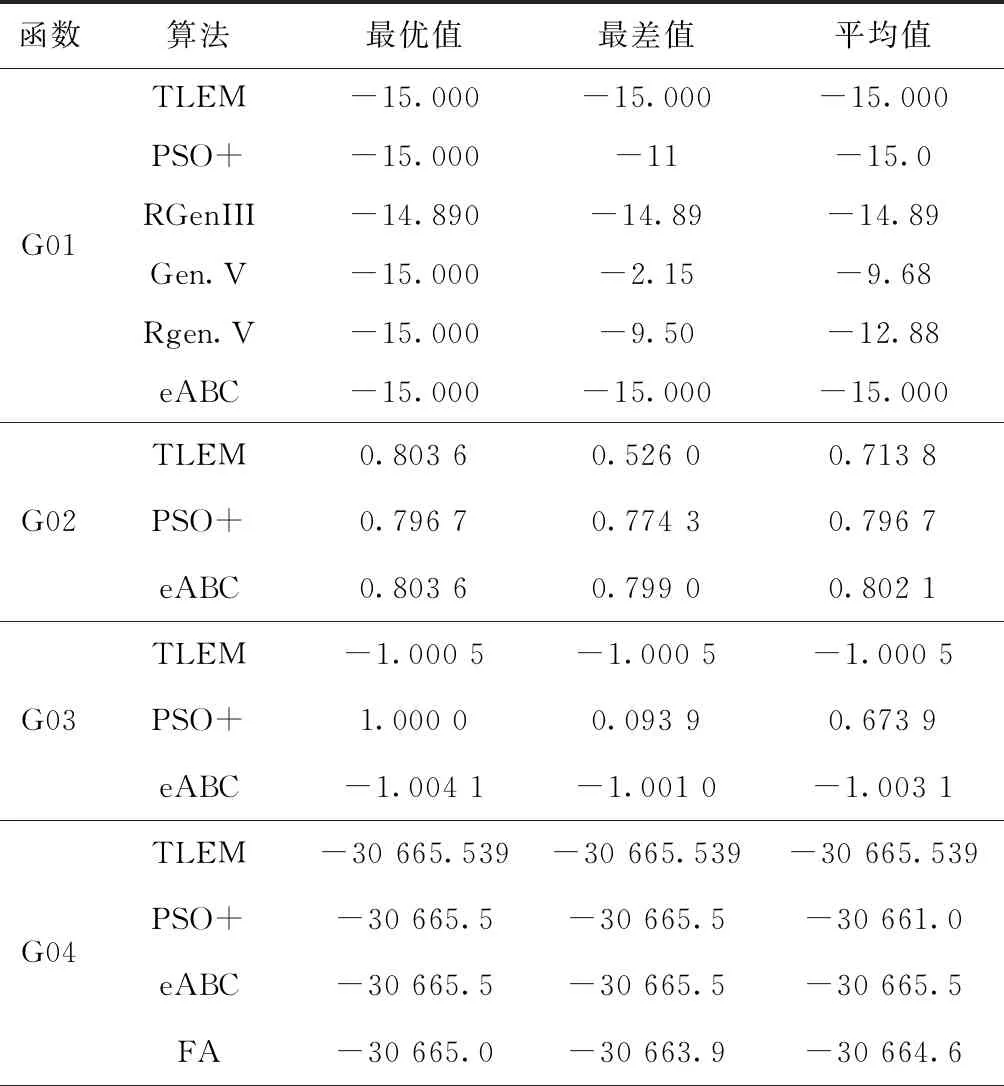
表6 TLEM与其他约束算法结果比较
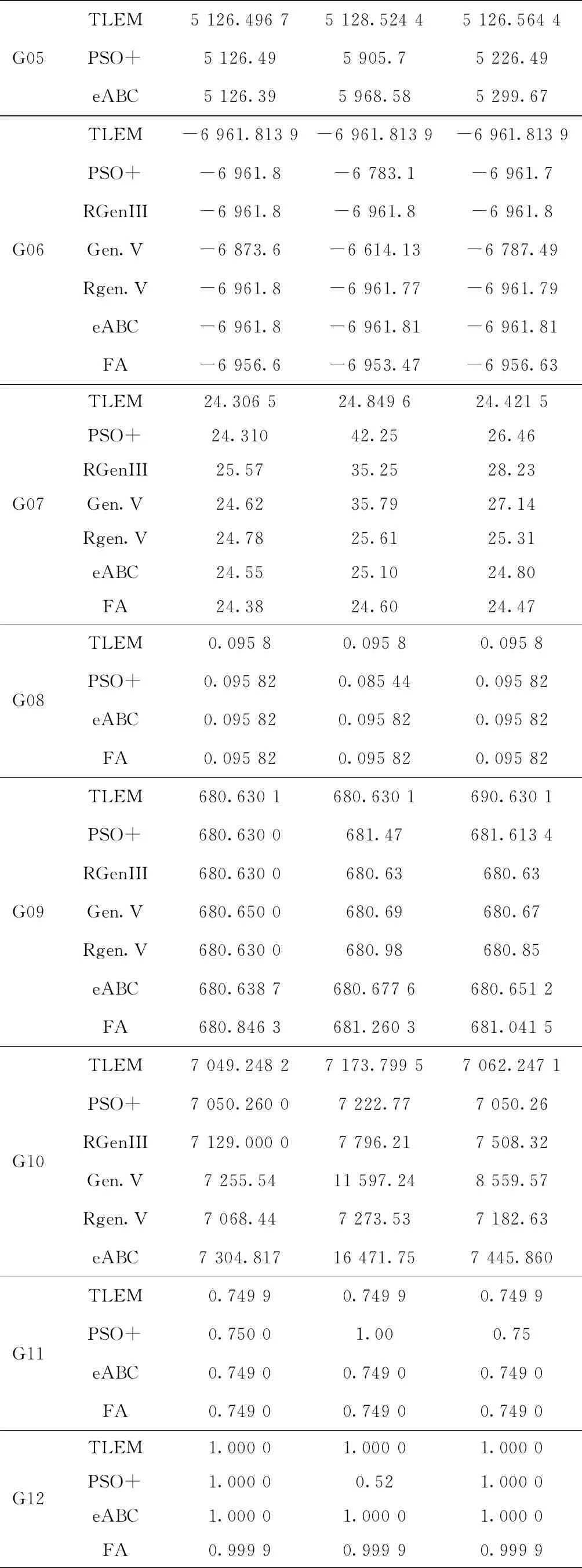
续表6

续表6
3 TLEM算法应用研究
3.1 压力容器设计
压力容器设计的目标是在满足生产需要的同时使其总费用f(x)最少,其4个设计变量分别为:外壳厚度Ts(x3)、封头厚度Th(x4)、内半径R(x1)以及容器长度L(x2,不包含头部),其中Ts和Th为0.062 5的整数倍,R和L为连续变量。图2为压力容器模型设计图,具体数学模型如式(13)和式(14)所示。
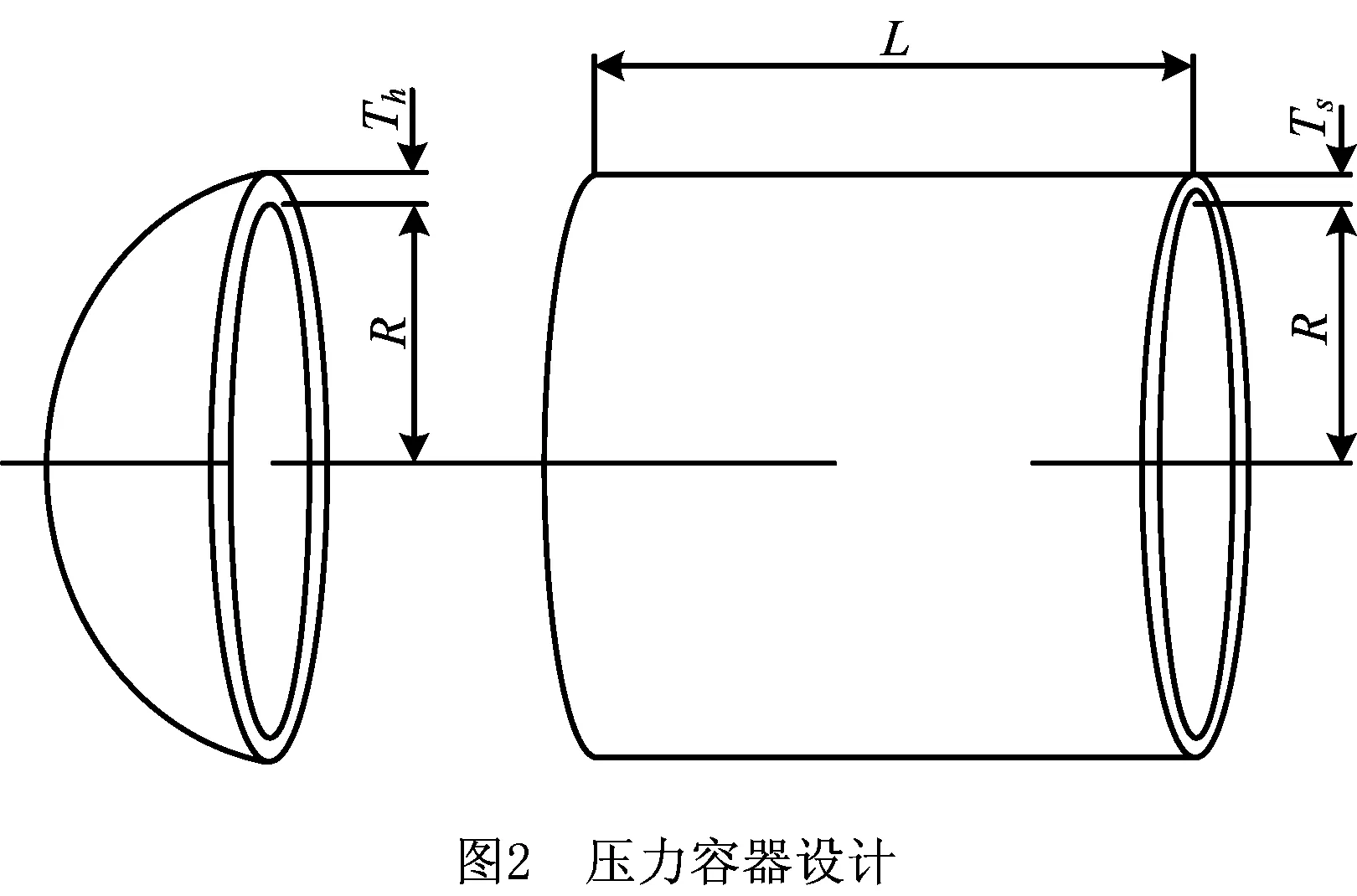
目标函数:
minf(x)=0.622 4x1x3x4+1.778 1x2x2x3+
g1(x)=-x1+0.019 3x3≤0,
g2(x)=-x2+0.009 54x3≤0,
(13)
约束条件:
g4(x)=x4-240≤0。
(14)
边界约束:
0≤x1≤99,0≤x2≤99,
10≤x3≤200,10≤x4≤200。
利用TLEM算法对压力容器设计问题进行求解,算法的相关参数设置如下:种群大小为50,移动概率MP=0.9,交换概率p=0.9,最大迭代次数为200。TLEM算法独立运行30次后得到目标函数最优值、平均值和函数评价次数,并且与文献[23-28]中各个学者的研究结果进行比较,统计结果如表7所示。
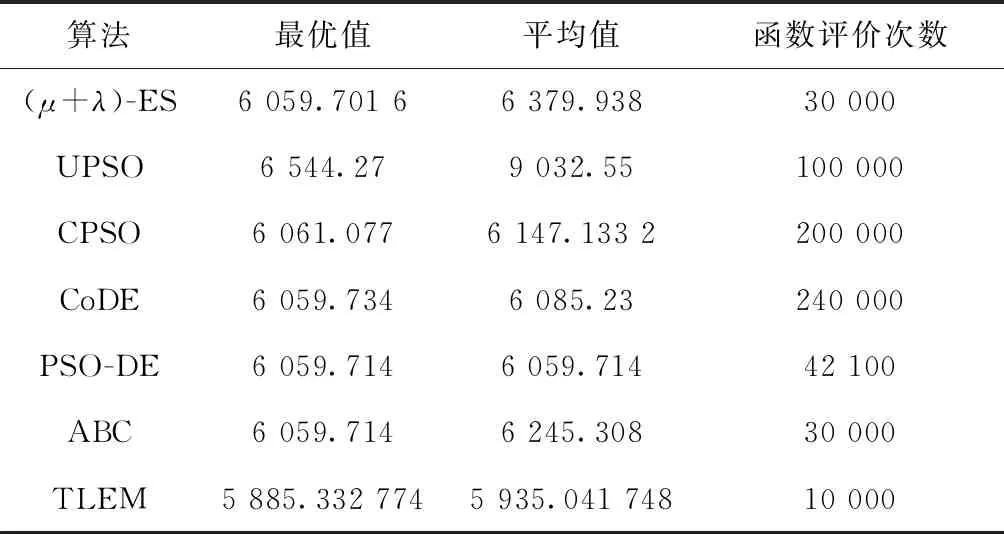
表7 压力容器设计问题统计结果
从表7可以看出,TLEM算法在30次独立运行中,不论是搜索到的最优值还是平均值均优于其他算法,同时所需要函数评价次数也是最少的,这表明TLEM算法不但具有很强的搜索能力,而且搜索效率也很高,能够在压力容器制造过程中更好地降低材料消耗成本。
3.2 压缩弹簧设计
压缩弹簧设计的目标是在满足一定约束条件下最小化其质量f(x),其中包含最小挠度、剪切应力、振荡频率以及外径限制4个不等式约束,弹簧圈平均直径D(x2)、弹簧金属丝直径d(x1)以及弹簧有效圈数N(x3)3个设计变量,如图3所示。其具体数学模型如式(15)和式(16)所示。
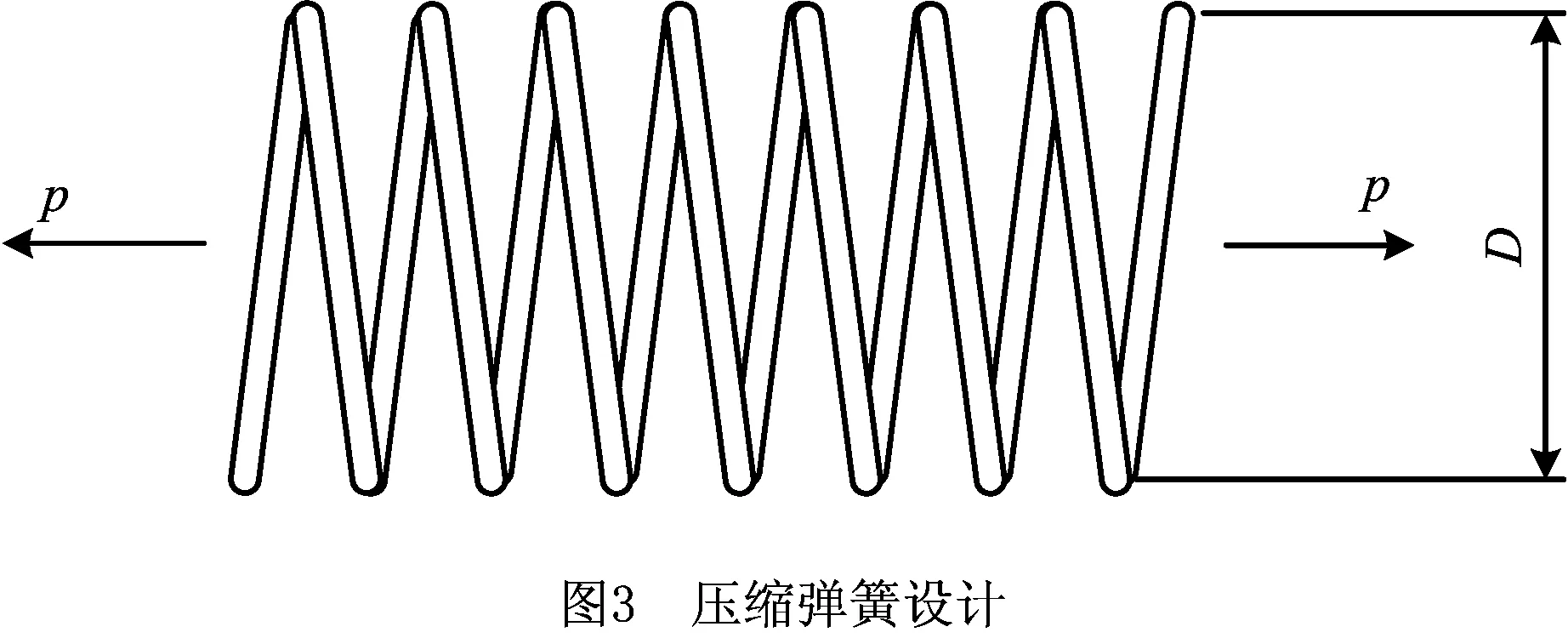
目标函数:
minf(x)=(N+2)Dd2。
约束条件:
(16)
边界约束:
0.05≤x1≤2,0.25≤x2≤1.3,2≤x3≤15。
利用TLEM算法对压力容器设计问题进行求解,算法相关参数设置如下:种群大小为50,最大迭代次数为200,移动概率为0.9,交换概率为0.9。TLEM算法独立运行30次后得到目标函数最优值、平均值和函数评价次数,并且与文献[23-28]中各个学者的研究结果进行比较,统计结果如表8所示。
从表8可以看出,在30次独立运行中,PSO-DE算法、ABC算法以及TLEM算法都取得了最好的最优值0.012 665,PSO-DE算法同时还取得了平均值上的最优,TLEM算法较之略差,但TLEM算法仍然是所需函数评价次数最少的算法,综上表明TLEM算法是一种有效的压缩弹簧设计优化方法。
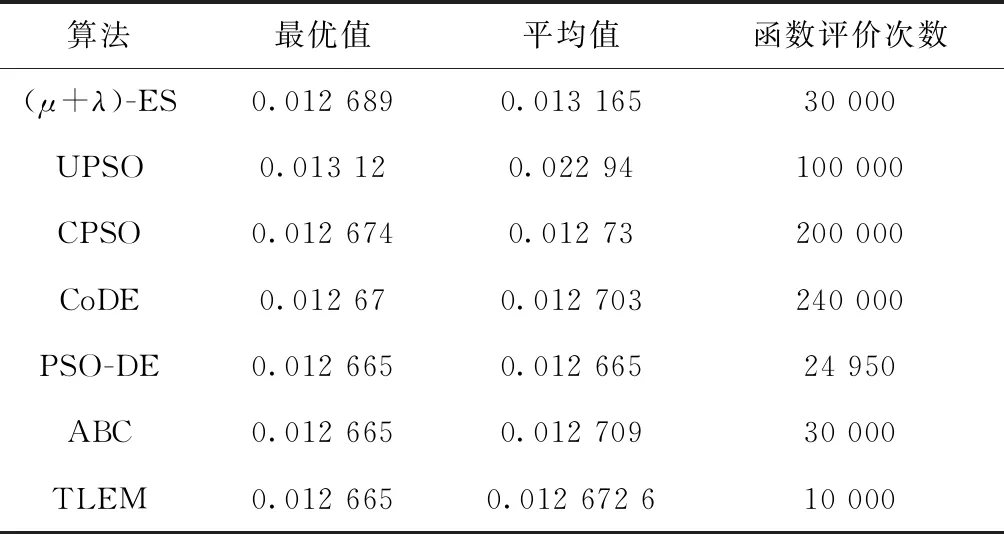
表8 压缩弹簧设计问题统计结果
3.3 焊接梁设计
焊接梁设计的目标是在满足一定约束条件下最小化其成本f(x),其中包含7个不等式约束分别为:剪切应力(τ)、梁的弯曲应力(σ)、杆件屈曲载荷(Pc)、梁端挠度(δ)等,4个设计变量分别为:h(x1)、l(x2)、t(x3)以及b(x4),如图4所示。其具体数学模型如式(17)和式(18)所示。
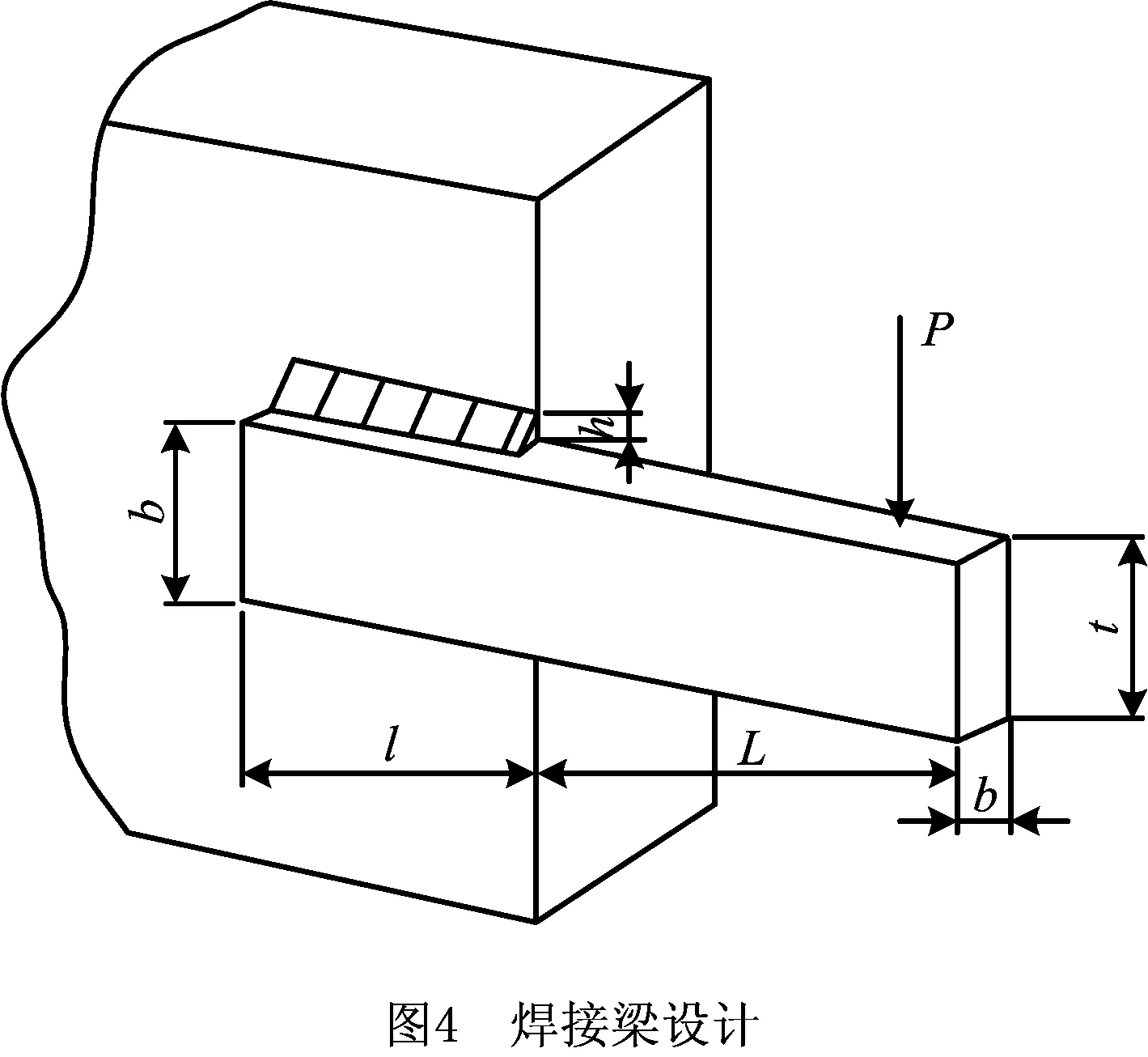
目标函数:
x3x4(14.0+x2)。
(17)
s.t.
g1(x)=τ(x)-τmax≤0,
g2(x)=σ(x)-σmax≤0,
g3(x)=x1-x4≤0,
x3x4(14.0+x2)-5.0≤0,
g5(x)=0.125-x1≤0,
g6(x)=δ(x)-δmax≤0,
g7(x)=P-Pc(x)≤0。
(18)
边界约束及相关参数值:
P=6 000lb,L=14in,E=30e6psi,
G=12e6psi,τmax=13 600psi,σmax=30 000psi,
δmax=0.25in,
0.1≤x1≤2.0,0.1≤x2≤10.0,
0.1≤x3≤10.0,0.1≤x4≤2.0。
利用TLEM算法对焊接梁设计问题进行求解,算法相关参数设置如下:种群大小为50,最大迭代次数为200,移动概率为0.9,交换概率为0.9。TLEM算法独立运行30次后得到目标函数最优值、平均值和函数评价次数,并且与文献[23-28]中各个学者的研究结果进行比较,统计结果如表9所示。
从表9可以看出,TLEM算法在30次独立运行中,不论是搜索到的最优值还是平均值均取得了最优,而且所需要函数评价次数也是最少的。其中(μ+λ)-ES算法和ABC算法在最优值上取得了和TLEM算法一样的结果,但这两种算法的平均值要比TLEM算法的差,而且它们的函数评价次数是TLEM算法的3倍。这表明TLEM算法无论是在搜索性能还是在搜索效率上都是这几种算法中最好的。
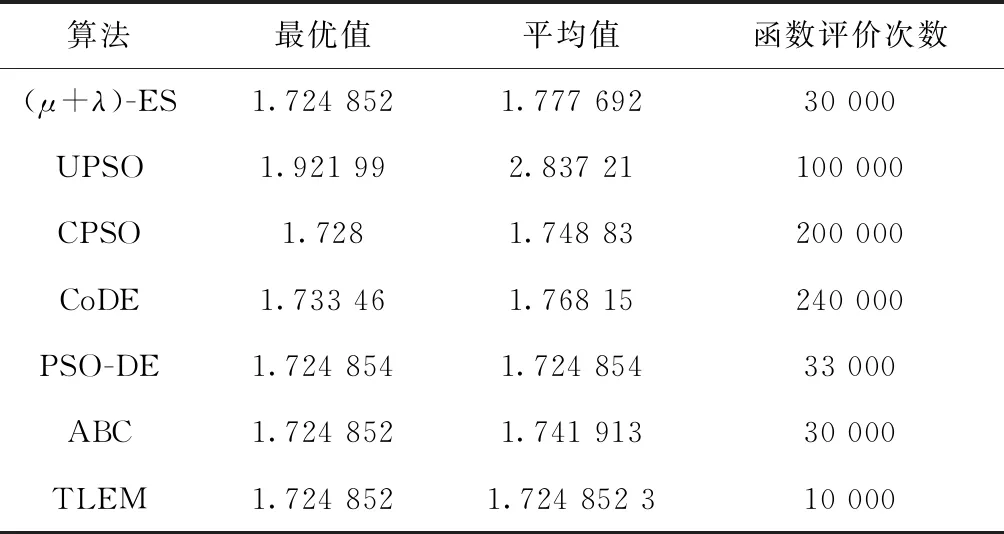
表9 焊接梁设计问题统计结果
4 结束语
本文针对EM算法的不足,提出一种基于师生交流机制的改进类电磁机制算法(TLEM)。该算法将教学优化算法和一种改进的类电磁机制算法相结合,用于解决约束优化问题。算法结合了TLBO算法和EM算法各自的优点,既具有较强的全局搜索能力,又具有较高的局部搜索精度。通过与其他版本的EM算法以及若干最新约束优化算法进行的标准函数测试实验,验证了TLEM算法具有稳定优良的寻优能力,是一种新型有效的约束优化方法。最后将TLEM算法应用到3个工程设计优化问题中,并与其他算法相比较,实验结果表明了TLEM算法在该类问题上的可行性和优越性。未来,仍需进一步提高算法的计算效率,还需考虑到有些实际工程应用问题为多目标问题,以及如何利用TLEM算法解决这类多目标问题。
