基于模式模糊识别的电动车双电机系统再生制动控制

李聪波，易 茜，胡 芮，朱道光，胡 捷

(重庆大学 机械传动国家重点实验室,重庆 400044)

0 引言

再生制动是电动汽车的特点之一，在制动时电动汽车通过反拖电机，使电机工作在发电状态，将刹车能量转换成电能储存在电池中[1]，可为驱动过程提供动力，提高电动汽车的续航里程。研究表明在城市工况下，多达50%的刹车能量可以被回收利用[2]。因此，再生制动是提高电动汽车续航里程的关键手段之一，而再生制动控制策略制定是否合理，对再生制动能量回收效果有很大影响。

目前，合理分配再生制动力和液压制动力是再生制动控制策略的主要研究内容。在保证制动安全性的前提下，应尽可能增大再生制动力，从而提高再生制动能量回收率。在电动汽车再生制动控制策略制定方面，一些学者展开了深入研究。Chen等[3]为探讨再生制动对电动汽车能量效率的影响，开展了基于两种评价指标和三种控制策略的实车实验，得出再生制动能量回收的评价标准。Xu等[4]以需求制动力、车速、电池核电状态(State of Charge，SOC)及电池温度为输入量，以再生制动力的大小为输出量设计了模糊辨识器，借助模糊识别合理分配摩擦制动力与再生制动力的大小，从而提高能量回收率。Maia[5]则以角速度、急动度和路面倾斜度为输入量，以制动力分配系数为输出量设计了模糊辨识器，并在此基础上制定了再生制动控制策略。

但是，上述研究均未考虑到进行再生制动时，多挡电动汽车传动比变化对电机发电效率的影响。在再生制动过程中，多挡电动汽车通过换挡操作，可以增大再生制动力的范围，提高电机发电效率，从而提高再生制动能量回收率[6]。基于此，Jo等[7]分析了在再生制动时六挡混动汽车的降挡原因，在降挡制动中，为了确保良好的制动力和驾驶舒适性，提出一种用于电子摩擦制动和再生制动的协同控制算法。Li等[8]以二挡变速电动汽车为研究对象，由已知的转矩和角速度获得理想换挡点，基于此制定了一种分层控制策略，以实现在降挡过程中再生制动和液压制动的联合控制；硬件在环试验结果表明，有降挡控制策略的试验组比没有降挡控制策略的试验组多回收27.44%的能量。Yeo等[9]在传统的CVT再生制动控制策略中增加了传动比控制策略，利用遗传算法优化传动比，仿真结果表明优化前后再生制动能量回收率提高8%。

近年来，考虑到电动汽车双电机动力系统的能量利用率高于单电机动力系统[10]，一些学者对电动汽车双电机动力系统展开研究。李聪波等[11]针对双电机动力耦合系统提出一种动力系统参数优化匹配的方法，利用多目标粒子群优化算法对动力系统参数优化模型进行求解，优化后的参数能有效提高电动汽车的动力性和经济性。Hu等[12]根据车速、加速度值、电池SOC对能量效率进行优化，决策双电机传动系统工作模式。Zhang等[13]为提高双电机动力耦合电动公交车工作效率，提出一种简单和适应性强的能量管理策略，基于两参数模式切换控制选取最优工作模式。

然而，以上关于双电机动力耦合电动汽车的研究侧重于传动系统结构和驱动能量管理策略，对制动过程中的再生制动策略研究较少。因此，本文以前驱纯电动汽车双电机传动系统为研究对象，提出一种兼顾电机效率和模式切换稳定性的再生制动控制策略。首先利用模糊控制原理，根据制动工况输出最大再生制动力分配系数；其次根据最大再生制动力、车速和电机MAP图，选择电机效率最高的再生制动模式。然后考虑到再生制动模式切换时会引起转矩波动影响整车平稳性，因此对冲击度进行计算和判断，保证再生制动模式切换的平稳性。最后在保证制动安全性和稳定性的前提下，根据I曲线分配双电机动力耦合电动汽车前后轮制动力。

1 双电机动力耦合电动汽车再生制动模式划分

1.1 电机效率分析

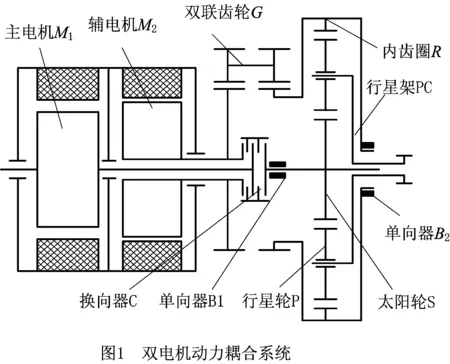
双电机动力系统用两个中小功率电机配合工作代替一个大功率电机，以提高电机效率和能量利用率。以课题组前期所研究的前驱双电机动力耦合系统[14]为研究对象，对其再生制动控制策略展开研究。该双电机动力耦合电动汽车结构简图如图1所示。

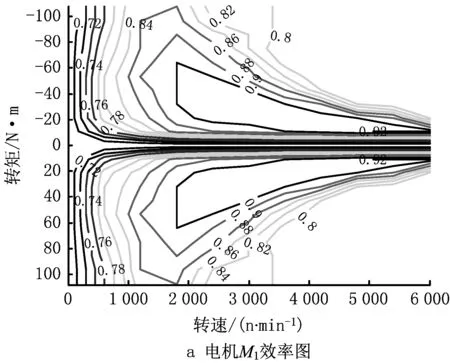
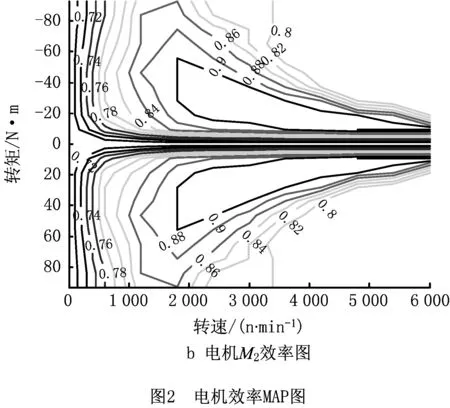
在相同再生制动情况下，电机发电效率越高，再生制动能量回收率也就越高。因此，明确该双电机发电效率分布情况能保证再生制动模式划分的准确性，从而使各个再生制动模式下电机效率最高。由此，以电机效率MAP图为依据，对再生制动模式进行划分，实测两个电机M1、M2的电机效率图如图2所示，其中M1为主电机，M2为辅电机。

基于实测双电机M1、M2的电机发电效率图，改变自动换向器C的工作位置，从而改变再生制动系统速比，使双电机再生制动系统进入不同的再生制动模式，此时电机分别工作在各自的高效发电区域，从而可以回收到更多的制动能量。由双电机动力耦合电动汽车驱动系统的前期研究可知，换向器C一共有3种工作状态，CL、CM和CR。换向器C与单向器B1、B2配合工作，形成4种再生制动工作模式。

表1 双电机再生制动系统工作模式

1.2 模式划分

多种再生制动模式的配合使用可使双电机动力耦合系统中的各个电机长时间工作在高效的发电区域，可以充分回收制动能量。基于电动汽车行驶工况，将车速分为3个区域：0～35 km/h是低速段、35～70 km/h为中速段、70～120 km/h为高速段。基于两个电机的效率分布图，以保证两个电机长时间工作在发电高效区域为目的，进行再生制动模式划分如表2所示。

表2 再生制动模式划分

下面对4种再生制动模式作详细分析：

(1)再生制动模式1 当换向器C处于右端工作状态时，齿圈在单向器B2作用下处于静止状态，此时电机M1单独工作发电。电动汽车车轮处产生的动能由行星架P输入，太阳轮S输出再反拖电机M1，从而使电机M1处于发电状态，将动能转换为化学能储存在电池中，如图3所示。电机M1单独工作时转速和转矩关系如式(1)和式(2)所示:

(1)

i0(α+1)T1=T3,

(2)

(3)

式中：n1为电机M1的转速，n3为车轮输入再生制动系统的转速，T1为M1的转矩，T3为车轮输入再生制动系统的转矩，i0为固定传动比，ZR为齿圈齿数，ZS为太阳轮齿数，α为行星轮系特征参数。

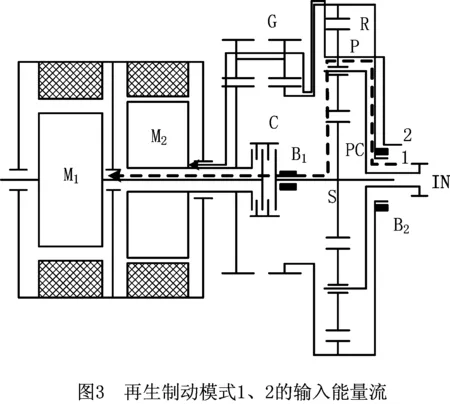
(2)再生制动模式2 当换向器C处于中间工作状态时，由表1可知电机M2与齿圈相接，如图3所示，此时电机M2单独工作在发电状态。M2单独工作时，电机的转速和转矩计算如式(4)和式(5)所示：

(4)

(5)

式中T2为电机M2转矩。

(3)再生制动模式3 当换向器处于左端工作状态时，两个电机都同时处于发电工作状态，电机M1、M2转矩耦合。车轮处产生的动能部分经过齿圈和换向器传向电机M1，同时剩余部分动能直接经齿圈传向电机M2，该制动模式下能量传递路径如图4所示。再生制动系统输入输出转速关系如式(6)所示：

(6)

在该再生制动模式下，由于两个电机同时工作回收制动能量，需对两个电机的转矩进行合理分配，保证两个电机同时工作在高效区域。根据电机相似性原则对双电机转矩耦合再生制动模式进行功率等比例分配，从而保证两电机效率较为近似且均较高[15]，此时，双电机转矩分配满足式(7)：

(7)

式中Pmax1、Pmax2分别为电机M1、M2的电机最大功率。

(4)再生制动模式4 电机M1、M2转速耦合，部分输入动能经过太阳轮和单向器B1传向主电机M1，同时剩余的动能直接经齿圈传递至电机M2，采用行星轮系进行转速耦合，如图4所示。电机M1、M2转速耦合时，双电机动力耦合系统的两个电机转矩关系如式(8)所示：

(8)

在该转速耦合再生制动模式下，需要对电机转速进行分配，从而提高电机发电效率。因此，基于前期研究，根据工作转矩下的最大转速进行分配，从而满足两个电机发电效率的最大化。两电机转速分配满足下式：

(9)

(10)

(11)

n1=knmax1，

(12)

n2=knmax2。

(13)

式中：T1、T2表示电机M1、M2处于发电工作状态时产生的再生制动转矩；nmax1、nmax2为电机M1、M2的最大转速；i1、i2为电机M1、M2单独工作时的减速比；v为汽车时速；k为转速比例系数n1、n2为转速分配后电机M1和M2的转速。

根据电机在发电工作状态下的最大制动扭矩绘制出电动汽车等效再生制动力图，基于以上对双电机再生制动系统所需再生制动力矩和此时车速大小的分析，对再生制动模式进行划分如图5所示。

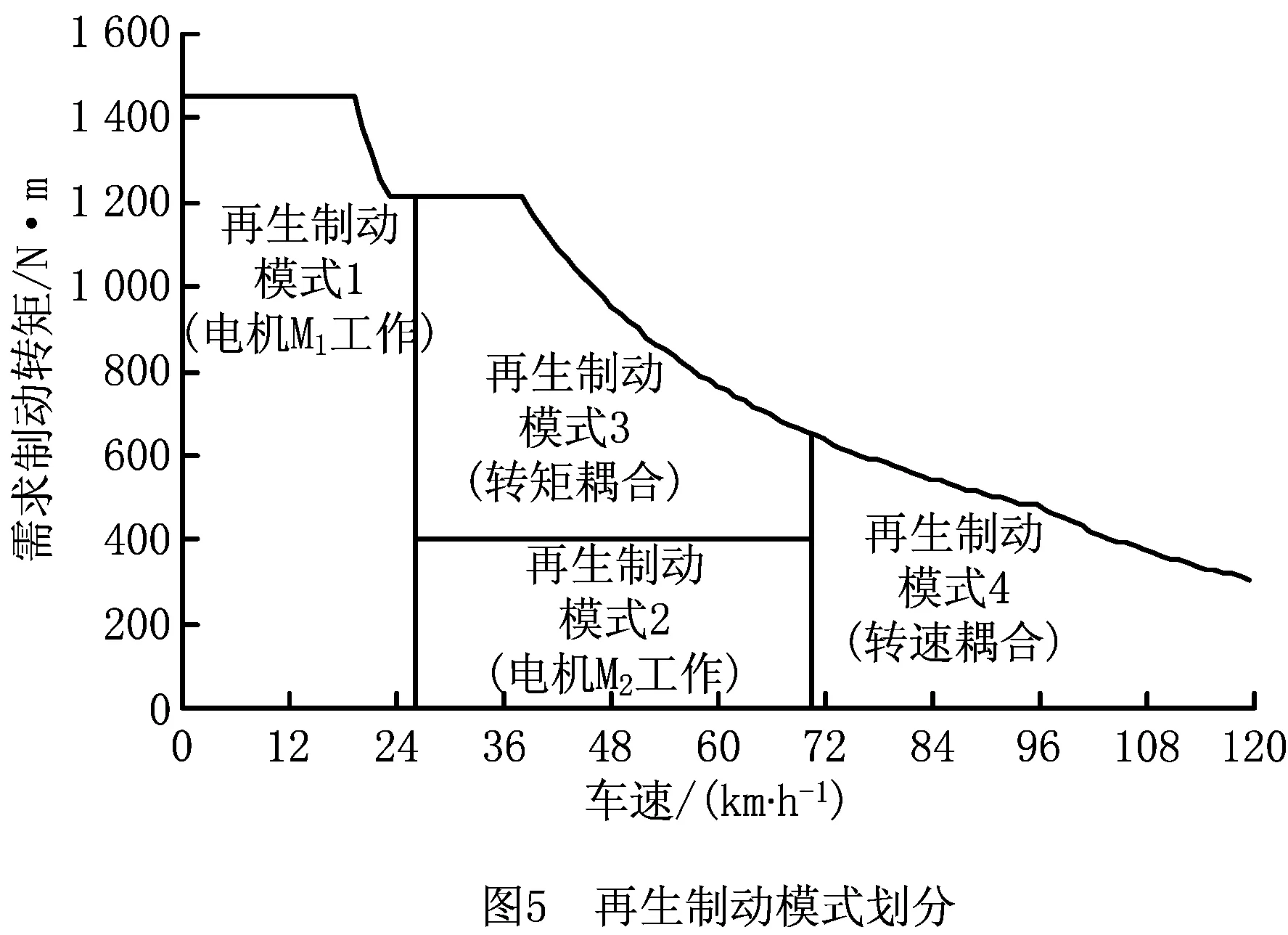
2 双电机再生制动模式的模糊逻辑识别

在保证制动安全性和电机发电效率的前提下，为提高再生制动能量回收率，应尽可能提高再生制动力在总制动力中的比例。在获取到此时的最大再生制动力后，可根据再生制动力和车速匹配到合适的双电机动力耦合电动汽车再生制动模式，使电机工作点位于高效发电区域。综上所述，获取最大再生制动力是保证匹配到合适再生制动模式的重要步骤。电动汽车制动过程中，再生制动力的大小受驾驶员制动意图、车速、电池等多种因素的影响，无法用一个具体的模型得到再生制动力的大小。模糊控制用语言式的模糊变量来描述系统，不必对被控制对象建立完整的数学模式，具有较好的鲁棒性，在不确定系统中广泛使用[16]。因此，采用模糊控制原理分配电动汽车再生制动力。在大量数据和经验的基础上，基于MATLAB软件，结合模糊控制原理设计了一个输入为踏板开度、踏板开度变化率、车速和电池SOC，输出为最大再生制动力分配系数的模糊识别器，从而获取可靠的最大再生制动力，最后匹配到合适的再生制动模式。

2.1 模式模糊识别器输入及输出参数

(1)输入参数

选择合理的再生制动意图识别参数能够保证模糊识别的准确性。在行驶过程中，安装在制动踏板上的角度传感器将驾驶员的制动意图转换成电信号，传送至控制器进行制动操作。踏板传感器所采集的信号包括踏板开度和踏板开度变化率。踏板开度越大，所需制动力越大。踏板开度变化率的大小能够反映出制动的紧急程度，制动踏板开度变化率越大，制动情况越紧急，所需的制动力也越大。考虑到这两个参数可以在第一时间直接反映出驾驶员的制动意图，因此踏板开度、踏板开度变化率是两个重要的再生制动意图识别参数。

此外，车速是保证制动安全性的一个关键影响因素，车速过低再生制动模式无法启动；车速过高时，只采用纯液压制动从而保证制动的安全性，因此选取车速作为再生制动意图识别的第3个参数。电池容量和最大允许充电电流虽然起到保护电机的作用，但是电池的这些局限会降低充电效率，从而降低能量回收率，因此本文选取电池荷电状态SOC作为第4个再生制动意图识别参数。

(2)输出参数

为确保再生制动力在安全范围内为最大值，且直观反映再生制动力的大小，则选取再生制动力在总制动力中所占比例γ，即最大再生制动力分配系数为模糊识别器的输出参数，

(14)

式中：Fzs为再生制动力矩，Fxq为总的需求制动力。

2.2 输入、输出参数的隶属度函数

考虑到计算的简洁性和较好的适应性，选取三角形—梯形型隶属度函数[17]设计踏板开度、踏板开度变化率、车速、电池SOC四个参数的隶属度函数。

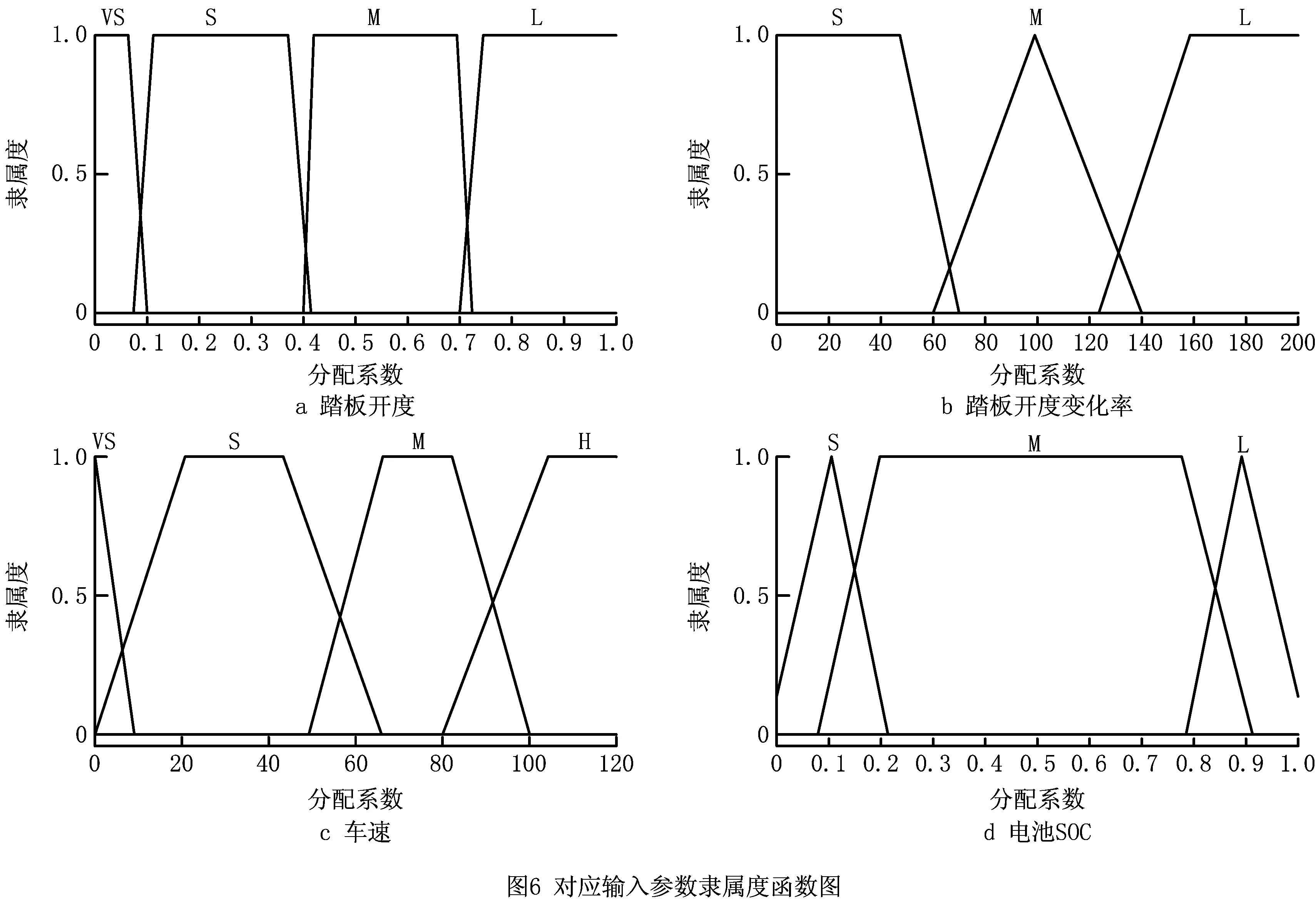
通过分析大量的实车工况数据，找到踏板开度、踏板开度变化率的范围，绘制出隶属度函数曲线。制动踏板开度的论域为[0,1]，对应的模糊子集为E(a)=[VS,S,M,L]，其中VS代表“很小”，S为“小”，M为“中”，L为“大”。制动踏板开度变化率的论域为[0,190]，对应的模糊子集为E(da/dt)=[S,M,L]，对应字母的含义如前所述。本文选取车速的论域为[0，120]，其对应的模糊子集为E(V)=[VS,S,M,H]，“H”表示“高”，隶属度函数曲线如图7所示。选取电池SOC的论域为[0,1]，对应的模糊子集为E(S)=[S,M,L]。输入参数的隶属度函数曲线如图6所示。

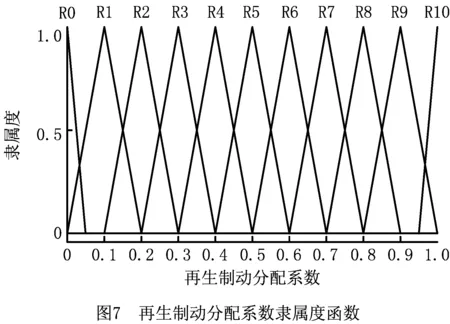
模糊控制输出参数最大再生制动力分配系数γ的论域为[0,1]对应于模糊子集E(γ)=[R0，R1，R2，R3，R4，R5，R6,R7，R8，R9，R10]，其隶属度函数曲线如图7所示。

2.3 模糊推理规则

模糊推理规则是模糊逻辑控制的核心。本文采用的模糊控制结构由4个输入量和1个输出量组成，模糊推理规则采用Mandani法，推理规则遵循：IfAandBandCandDthenE。结合实际情况，逐一改变输入参数的值，从而依次制定出模糊推理规则。根据隶属度函数可知，共有144条模糊推理规则，其部分推理规则如表3。模糊推理规则遵循以下规律：

(1)踏板开度越大，所需制动力越大，最大再生制动力分配系数越大。

(2)踏板开度变化率增大，表明驾驶员制动意图越来越强烈，所需制动力越大，最大再生制动力分配系数也越大。当踏板开度变化率达到紧急制动状态时，为了保证制动安全性，进入紧急制动模式，最大再生制动力分配系数为0。

(3)当车速很低时，无法启动再生制动系统，此时再生制动力为零，最大再生制动力分配系数为0；当车速低时，为了确保制动安全性和满足相关法规规定，再生制动力在总制动力中所占比例较小，最大再生制动力分配系数较小；当为中挡车速时，在满足电机性能要求下，再生制动力越大越好，最大再生制动力分配系数增大，但受到电机性能的限制，再生制动力不能无限增大，最大值为电机能产生的最大制动力矩，最大再生制动力分配系数为1。当车速高时，保证制动安全性，不进行再生制动，最大再生制动分配系数为0。

(4)当电池SOC<0.1时，电池的内阻很大，此时电池并不适合工作在充电状态，因此此时再生制动力占总制动的比例很小，最大再生制动力分配系数很小；当电池SOC值在0.1～0.9时，电机反拖产生大电流对电池进行充电，此时再生制动力所占比例相应的增加，最大再生制动力分配系数也相应增大；当电池SOC>0.9时，为保护电池，充电电流将减小，此时再生制动力为零，最大再生制动力分配系数为0。

表3 推理规则表

3 双电机再生制动控制策略设计

本文所提双电机再生制动控制策略由再生制动模式选择模块和制动力分配模块组成。首先根据当前制动工况信息，采用模糊控制原理输出再生制动模式。此时，存在模式切换的情况，为保证模式切换时整车的平稳性，在设计再生制动控制策略时考虑整车冲击度，对是否进行制动模式切换进行判断。为保证制动的安全性，采用理想制动分配曲线I曲线分配前后轴制动力[18]。

3.1 再生制动模式选择模块

根据车辆制动性能要求，制动踏板开度α与制动减速度a呈线性关系，因此可根据制动踏板开度α得到与之对应的制动减速度值a，从而由式(15)计算出需求制动力Fxq的大小。借助MATLAB/SIMULINK平台，设计了模糊识别器，通过模糊处理可获得最大再生制动力分配系数γ，从而通过式(16)计算得到再生制动力的大小，即电机在发电过程中产生的制动力。再根据式(17)计算出此时的再生制动力矩的大小。

Fxq=ma，

(15)

Fzs=γFxq，

(16)

(17)

式中：m为整车质量，Fzs为再生制动力，Tzs为再生制动力矩，rw为车轮半径，ik表示第k种制动模式下的传动比，ηT为传动系效率。

如果再生制动力矩Tzs大于电机所能提供的最大制动力矩Tmax，此时的再生制动力矩等于Tmax，剩下的制动力则由液压制动力进行补偿。电机能提供的最大制动力矩：

(18)

式中：Uchg为充电过程中电池端电压，Ichgmax为最大充电电流，ωn为电机角速度，ηm为电机发电效率。

将双电机动力耦合系统再生制动模式划分的规则(如图5和表2)储存在电动汽车整车控制器中，基于再生制动模式划分的表格，根据模糊识别得到的再生制动力和此时的车速，通过查表的方式匹配到合适的再生制动模式。该再生制动模式下的速比可以保证电机工作在高效的发电区域，从而提高电动汽车再生制动的能量回收率。

3.2 制动力分配模块

研究对象为前驱式电动汽车，因此在前轮进行再生制动，前轮的制动力由电机产生的再生制动力和电动汽车液压制动系统提供的液压制动力共同组成，后轮只有液压制动力作用。在保证电动汽车制动安全性的前提下，制动力分配模块的主要作用是合理分配3种制动力的大小。

当电动汽车前后轴制动力分配符合理想制动力分配曲线(Ⅰ曲线)时，地面附着力可以被电动汽车充分利用，从而保证汽车制动的稳定性。因此，采用理想的前后轮地面制动力分配Ⅰ曲线对前后轮制动力进行分配。前轮地面总的制动力

Fq=zmg(b+zhg)/L。

(19)

式中：b为汽车质心至后轴距离，hg为汽车质心高度，L为汽车轴距。

因为研究对象为前驱电动汽车的双电机系统，所以再生制动力全部作用于电动汽车的前轮，同时前轮制动力由再生制动力和液压制动力共同组成，因此前轮液压制动力

Fq1=Fq-Fzs。

(20)

根据Ⅰ曲线，对前后轮制动力进行分配，得到后轮的制动力

(21)

3.3 考虑模式切换平稳性的再生制动控制策略

再生制动控制策略包含仅有再生制动力作用、仅有液压制动力作用、再生制动力与液压制动力共同作用3种制动方式。汽车制动时的减速度与重力加速度的比值称为制动强度z，其反映了驾驶员制动的制动意图，则根据制动强度z对制动方式进行划分，如表4所示。

表4 双电机电动汽车制动方式划分

当再生制动开启后，进入再生制动模式选择模块，根据当前制动工况，采用模糊控制原理输出最大再生制动力分配系数，根据该系数和车速匹配到电机发电效率最高的再生制动模式。此时可能存在再生制动模式切换的情况，模式切换前后的速度差会引起转矩波动，影响整车制动的稳定性[19]。本文采用冲击度J来表示模式切换时的整车的平稳性，德国标准要求冲击度小于10 m/s3，国标冲击度推荐值为小于17.64 m/s3。

为保证制动模式切换时的稳定性，在设计再生制动控制策略时，首先根据式(22)计算冲击度J的大小；然后根据制动模式切换时的冲击度对是否进行模式切换进行判断，若冲击度值小于德国标准要求的10 m/s3，则进行模式切换，否则按原有双电机工作模式进行制动。

(22)

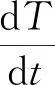
在再生制动控制策略的作用下3种再生制动方式切换使用，根据模式切换时的冲击度值对是否进行模式切换进行判断。从而在保证模式切换稳定性和制动安全性的前提下提高再生制动能量回收率，具体实现步骤如下(如图8)：

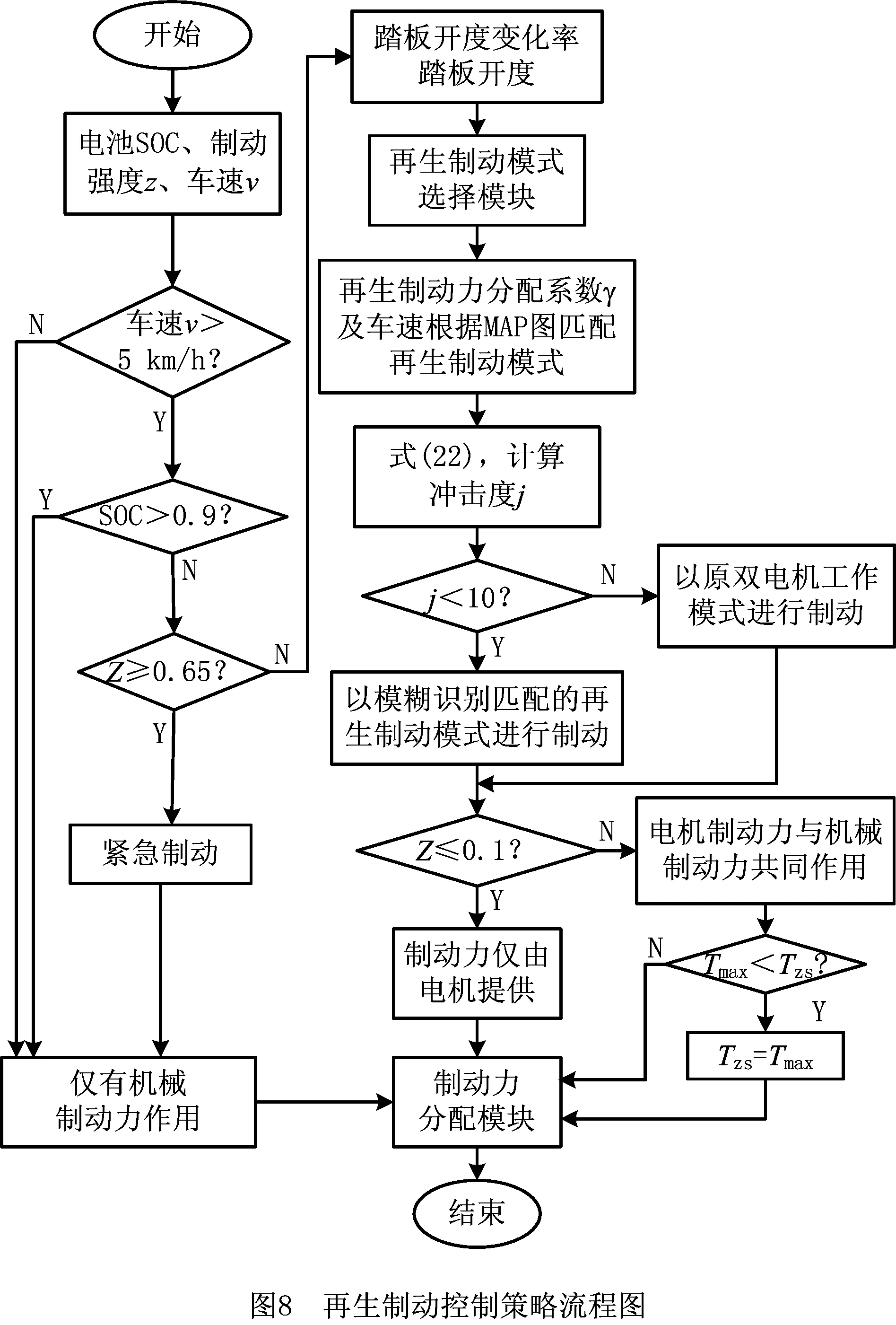
(1)输入踏板开度、踏板开度变化率、车速、电池SOC。

(2)车速过低，可用于回收的制动能量较少，为了保护电动汽车制动的稳定性不进行再生制动。因此，当车速小于5 km/h，不开启再生制动模式，制动过程中只有液压制动力起作用；车速大于5 km/h，开启再生制动模式。

(3)判断电池SOC值，为了保护电池，当SOC>0.9时不进行再生制动，制动力全部由液压制动力提供；当SOC<0.9时开启再生制动模式。

(4)当制动强度大于0.65时，制动力全部都由液压制动力提供；当制动强度小于0.65时，开启再生制动模式。

(5)开启再生制动模式后，进入再生制动模式模糊识别模块，从而获得再生制动力的值。利用再生制动力的大小和当前车速匹配到再生制动模式。

(6)计算模式切换时的冲击度，如果冲击度值大于10 m/s3，不进行模式切换；若小于10 m/s3则进行模式切换。

(7)对制动强度进行再次判别，当制动强度小于0.1时，制动力全部由电机发电产生；当制动强度大于0.1时，随着制动强度的增大，电机产生的再生制动力随之增大。由于电机性能会限制再生制动力的大小，当前轮所需制动力大于电机所能提供的最大制动力矩时，再生制动力取电机所能提供的最大再生制动力，同时剩下的制动力由液压制动力进行补偿。

(8)进入制动力分配模块，利用理想I曲线分配前后轮制动力，最后得到再生制动力、前轮液压制动力、后轮制动力的值。

4 仿真分析

4.1 控制策略整车仿真分析

利用MATLAB/SIMULINK仿真平台对所设计的基于模式模糊识别的双电机再生制动控制策略进行整车仿真分析，整车参数如表5所示。在仿真模型中，前轮的制动力由再生制动力和液压制动力共同组成，而后轮只有液压制动力作用，且只有前轮的制动能量可以被回收。

表5 整车参数

搭建仿真平台时，电池的充电效率包括电池充电电能效率和电池库伦效率的乘积[20]：

(23)

式中：E为电池电动势；I为电池电流；R为电池内阻；Idis、Ichg分别为电池的放、充电电流；tdis、tchg为电池放、充电时间。

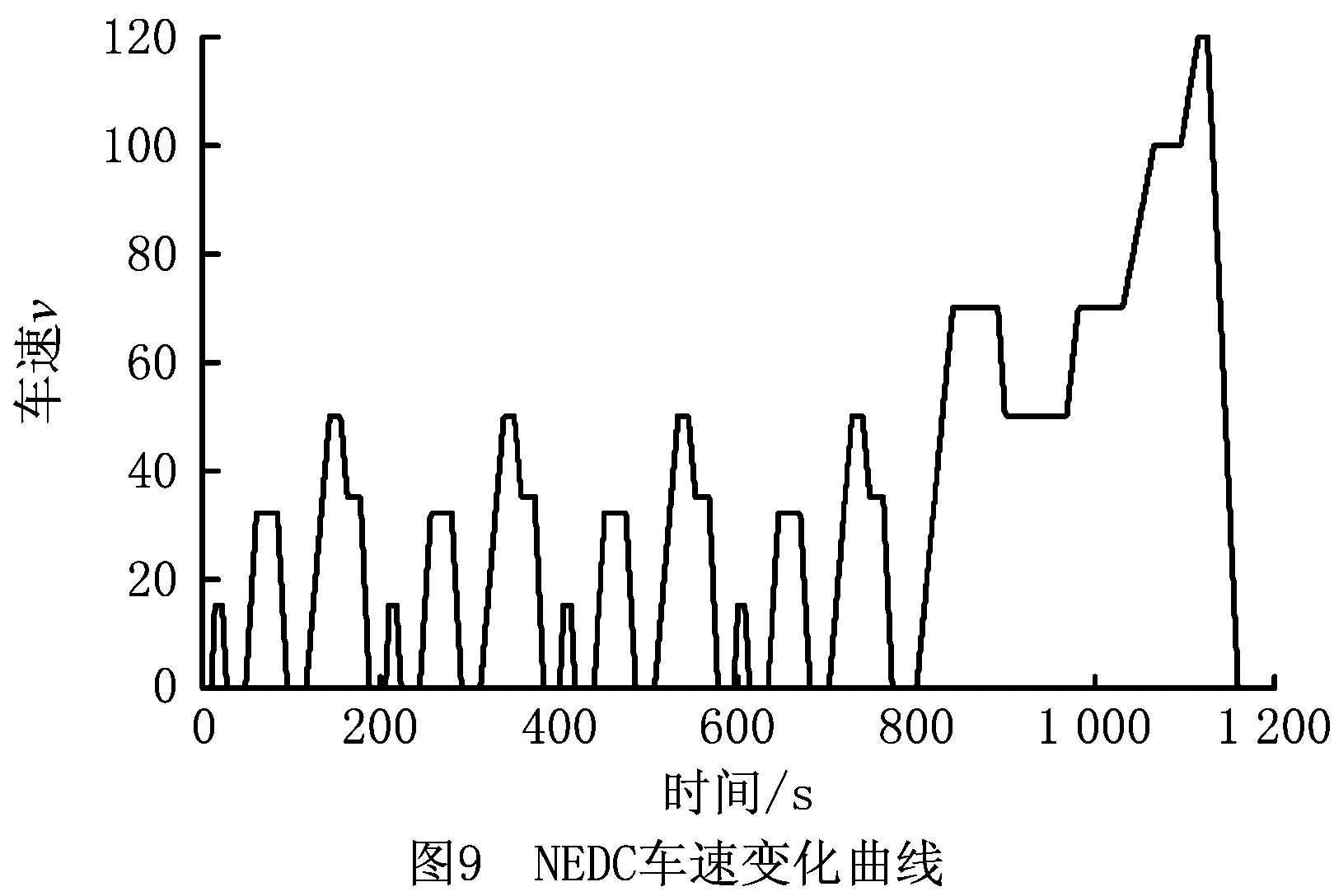
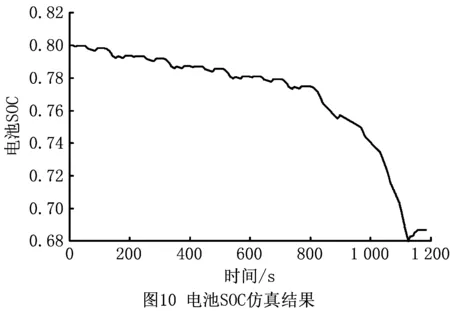
在新欧洲行驶循环工况(New European Driving Cycle，NEDC)下进行了仿真分析，设置初始电池SOC的值为0.8。NEDC工况下车速的变化如图9所示，电池SOC的仿真结果如图10所示。由图9和图10可知，在一个完整的NEDC循环工况下，当车速增加时，电动汽车的两个电动机处于驱动状态，输出能量从而使电动汽车车速增大，电池放电消耗能量，因此图中SOC值降低。当车辆处于制动状态，再生制动模式开启，此时两个电机处于发电状态，把车辆的刹车能量转化为电能储存在电池中，则电池SOC值增大。该仿真结果与理论分析结果一致。

为了验证该再生制动控制策略的有效性，在NEDC工况下对整车的再生制动模式选择情况和两个电机效率点的分布情况进行了仿真。由图11可知，当车速较低时，开启再生制动模式1，电机M1单独工作，且90%的情况下电机M1电机效率在85%以上，效率较高；当车速较高时，开启再生制动模式2或3，电机M2单独工作或电机M1和M2转矩耦合，电机M1和电机M2的平均效率为87%；当车速增大至高于70 km/h时，开启再生制动模式4，电机M1和M2转速耦合工作，效率点大多分布在高效区间。由图9可知，NEDC工况下处于较高车速的时间不长，因此选择再生制动模式4的情况较少，符合实际情况。通过以上分析可知，再生制动模式仿真结果与理论模式分析结果一致，基于模式选择的再生制动控制策略符合实际要求。

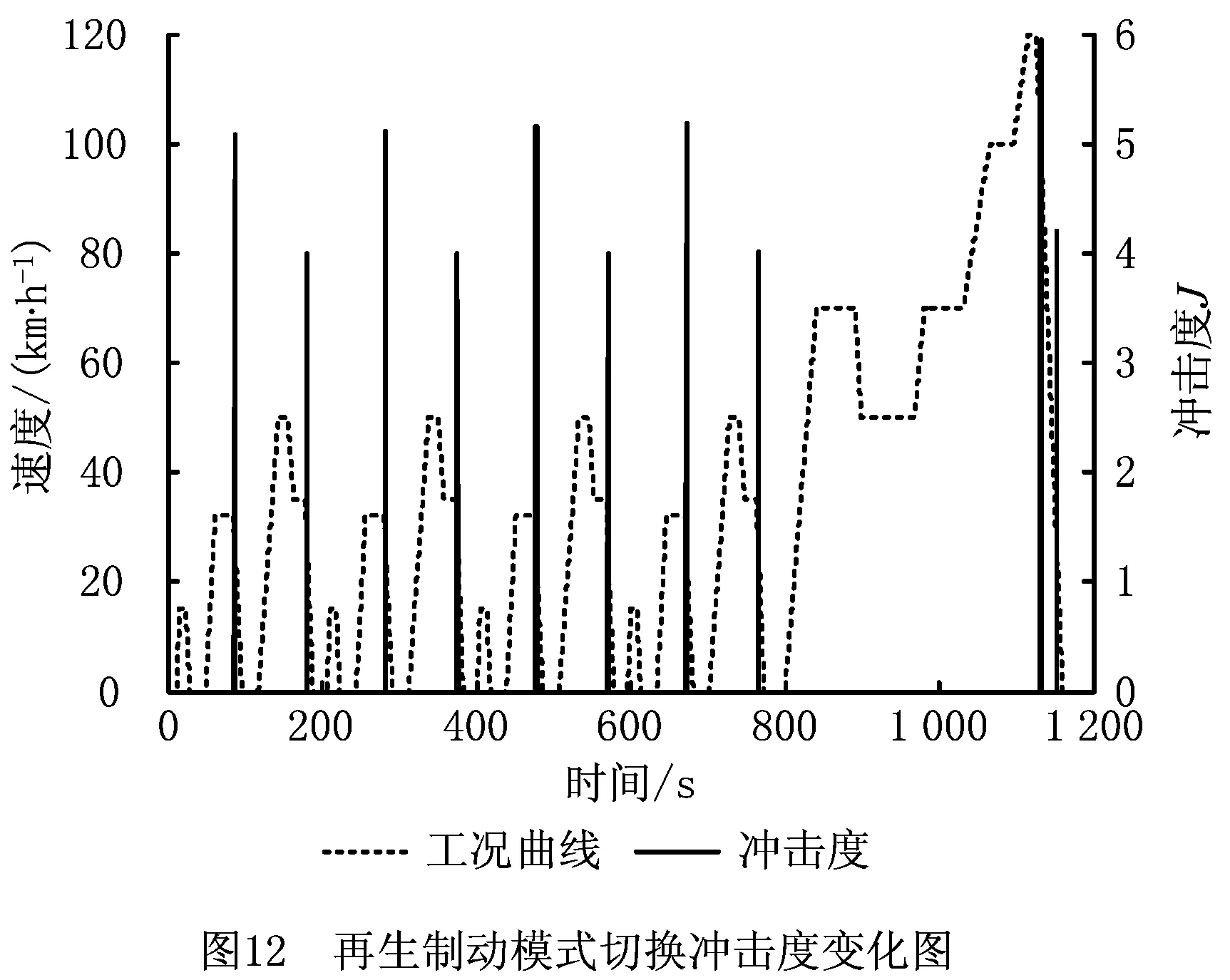
NEDC工况下模式切换过程冲击度变化如下图所示，由图(12)可知，冲击度值均小于10 m/s3，验证了本文所制定的再生制动控制策略在制动模式切换时的平稳性。

4.2 对比分析

为了更好地验证该再生制动控制策略在能量回收方面的优势，在NEDC工况下，将本文所提双电机再生制动控制策略与只利用功率较小的辅电机M2发电进行再生制动的控制策略进行仿真对比分析，能量回收情况如图13所示。

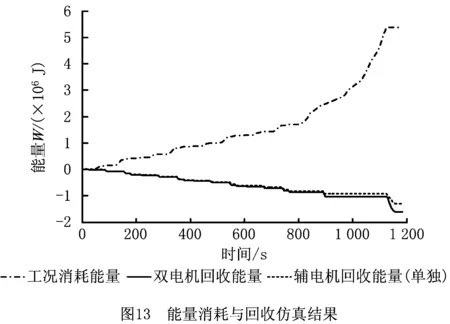
由图13可知，在一次NEDC循环工况下，双电机动力耦合电动汽车完成一次循环工况总共消耗的能量约为5.383×106J。本文将通过再生制动回收的能量与总的消耗能量的比值称为再生制动能量回收率。采用本文所提再生制动控制策略进行循环工况整车仿真时，结果表明通过再生制动回收的能量约为1.501×106J，能量回收率为27.9%。采用对比再生制动控制策略时，回收的能量约为1.315×106J，能量回收率为24.4%。双电机电动汽车采用基于模式模糊识别的再生制动控制策略回收的能量比只采用辅电机发电的再生制动策略回收的能量多14.3%，具有良好的能量回收效果。

综上所述，基于模式模糊识别的再生制动控制策略可以满足驾驶员的制动意图要求，同时在保证模式切换平稳性的前提下，可以提高电动汽车的能量回收率。

5 结束语

本文提出了基于模式模糊识别的再生制动控制策略,以保证两个电机工作在发电高效区域为目标，分析得到了4种再生制动模式。在不同制动工况下，4种制动模式相互切换使用，提高各个电机的发电效率，从而充分回收制动能量，提高再生制动的能量回收率。利用模糊控制原理，设计了一个模糊识别器用于再生制动模式的选择。该模糊识别器以制动踏板开度、制动踏板开度变化率、车速、电池SOC为输入，再生制动力系数为输出。再根据输出的再生制动力系数和车速，匹配到了合适的再生制动模式。为保证制动模式切换的稳定性，根据冲击度对制动模式切换进行判断。

仿真结果表明，在NEDC循环工况下，双电机电动汽车采用文中所提出的再生制动控制策略，再生制动能量回收率为27.9%，与只采用辅电机发电的再生制动控制策略相比，能量回收率提高14.3%，具有明显的节能效果。同时，在本文再生制动控制策略下，制动模式切换的冲击度值满足德国标准，保证了再生制动模式切换的稳定性。

本文主要研究了电动汽车双电机系统的再生制动控制问题，然而双电机动力耦合装置在模式切换的过程中具有动力耦合变化与迟滞等特性，所以模式切换过程中的再生制动力变化同样会对再生制动回收的能量与车辆冲击度产生影响。因此，探究双电机系统模式切换过程中再生制动力变化和再生制动回收的能量、车辆冲击度的关联关系将是下一步的研究重点。