两阶段动态差分智能元胞机算法

王亚良，倪晨迪，曹海涛，钱其晶，金寿松

(浙江工业大学 机械工程学院，浙江 杭州 310023)

0 引言

在工业领域如计算机科学[1-2]，航空航天工程[3-4]和机械制造[5]等存在大量的多目标优化问题(Multi-objective Optimization Problems, MOPs)，MOPs的子目标间可能相互冲突，所有子目标不能同时达到最佳。在工程实践中需对它们进行妥协折中处理，期望得到一个非支配解集(Non-dominated solutions)，集合中每个解都是帕累托最优(Pareto optimum)，被绘制在目标空间时即为帕累托前端(Pareto front)。传统的优化方法在求解MOPs时存在求解困难或多样性收敛性不佳的问题[6]。进化算法(Evolutionary Algorithms，EA)是一种基于种群的启发式搜索算法，可分为4类[7]：遗传算法(Genetic Algorithm，GA)、遗传规划(Genetic Programming，GP)、进化策略(Evolution Strategy，ES)和进化规划(Evolution Programming，EP)。进化算法比较适合处理MOP，目前比较经典的求解MOPs算法如NSGA-Ⅱ(Non-dominated Sorting Genetic AlgorithmⅡ)[8]，PAESⅡ Pareto Envelop-based Selection Algorithm Ⅱ)[9]和SPEA2(Strength Pareto Evolution Algorithm 2)[10]等。

元胞遗传算法(Cellular Genetic Algorithm，CGA)是融合CA与GA优点整合而成的一种新GA，算法的核心思想是将遗传算法的种群分布在二维细胞网格上，每个个体都占据一个特定的元胞并定义该元胞的状态[11-12]。许多学者在这方面开展了卓有成效的研究和探索。Kirley[13]提出了一种基于灾变机制的CGA，改变了原有种群分布，提高了种群的多样性。文献[14-15]从元胞的种群结构出发对算法进行改进分别提出分层CGA和自适应种群邻居的CGA。Alba等[16]提出了元胞多目标遗传算法(Cellular Multi-Objective Genetic Algorithm，CMOGA)。Nebro等[7]对CMOGA其进行改进，增加了外部种群的反馈机制，提出了MOCell，提升了算法局部寻优能力。之后，Durillo等[17-18]把差分进化算法(Differential Evolution，DE)与MOCell进行了耦合，并提出了用于解决多目标复杂工程问题的元胞差分算法(Celluar Differential Evolution, CellDE)，并取得了不错的效果。文献[19-20]将CellDE分别用于求解机组排班多目标问题和移动自组织网络，进一步验证了CellDE兼具MOCell和DE的优点。张屹等[21]利用CellDE算法求解车间布局优化问题的Pareto解集，詹腾等[22]提出基于多策略差分进化的元胞多目标遗传算法，验证了CellDE结合了MOCell和DE的优点。王亚良等[23]提出外部种群完全反馈的元胞差分(New Cellular Differential Evolution, NCe11DE)算法。Azizipour等[24]提出了一种新的遗传算法与元胞机相结合的混合算法，用遗传算法处理问题的可靠性部分，用CA方法解决问题的可操作性部分。GAN等[25]在元胞机基础上提出了双向进化优化的混合元胞机算法，具有计算效率高和稳定性好的特性。Redjepov等[26]提出了二维元胞机的可逆性算法。

CA是描述自然界复杂现象的数学模型，它主要由元胞、元胞空间、邻居和演化规则构成。目前将CA应用于GA的研究大体分为两类：第一类用CA丰富的演化规则来替代传统GA中的某些遗传操作；第二类则以复杂系统理论为基础，它将种群中的个体分配到元胞空间中，借助CA模型的邻居结构来实现GA的操作。CA理论研究主要包括前向问题即元胞机的分析和反向问题即元胞机的综合，CA模型属于“微观”模型，需要融合其他方法才能取得较为理想的解决方案。

为此，本文将智能体(Agent)机制引入元胞种群，并通过对元胞机个体邻居结构进行调整，实现进化种群由结构化种群过渡至非结构化种群，采用两阶段的外部种群多样性维护方法，将扰动因子引入变异操作避免陷入局部最优，引入多智能体方法和差分演化策略等来弥补CA的不足，提出一种外部种群充分引导的两阶段动态差分智能元胞机算法(Dynamic Differential Evolution Agent Cellular Automata，DDEACA)。通过三目标WFG系列函数对算法进行测试和分析，验证了DDEACA算法的有效性，能较好地兼顾全局搜索和局部寻优之间的协同问题。

1 元胞差分及其改进算法

Durillo等[18]在MOCell中引入差分进化操作，提出了基本的多目标元胞差分算法(CellDE)，CellDE在解决三目标优化问题时获得了质量较好的Pareto前端。CellDE采用近似DE/rand/1的变异方式，其基向量不是随机选择的，而是当前进化个体，故DE的父本由当前个体和两个邻居构成。设种群规模为N，d为解空间的维数。Xr1、Xr2、Xr3为3个父本向量，Vi为变异向量，Ui为子代向量，其主要内容如下。

(1)变异操作

Vi.j=Xr1.j+F(Xr2.j-Xr3.j),i∈[1,N],

j∈[1,d]。

(1)

式中F为介于[0,1]间的缩放因子。

(2)交叉操作

(2)

式中：randi.j为[0,1]之间均匀分布的随机数，CR为介于[0,1]间的交叉常量，randj(i)∈[1,2,…,d]。

外部种群完全反馈的元胞差分算法(NCellDE)作为元胞差分算法的典型改进算法，与传统的CellDE相比，在外部种群的多样维护机制、种群个体优劣评判标准和外部种群反馈机制都进行优化和改进，取得较好的效果[23]。

2 两阶段动态差分智能元胞机算法(DDEACA)

DDEACA是基于NCellDE算法而提出的，同时将Agent机制引入CA空间封装并扩展为具有自主性的智能型元胞机，充分利用Agent的自治特性，并结合结构化种群(元胞种群结构)和非结构化种群的优点，对个体(元胞)的邻居结构进行变化，将个体的邻居结构(如Moore型)扩大至整个进化种群，通过对个体的邻居结构进行调整，实现进化种群由结构化种群过渡到非结构化种群的效果，更好地实现全局寻优和局部寻优之间的平衡；同时为了减少算法对外部种群的维护时间开销，并提高算法的收敛速度，对外部种群保留的对象进行调整及完全反馈。邻居结构的变化将整个进化过程分成两个阶

段。在进化的第一个阶段，外部种群并不一定要保留非支配解；在进化的第二阶段，外部种群保留非支配解，同时一旦外部种群中的非支配个体超过预定规模，就立刻对外部种群进行修剪。邻居结构和外部种群保留对象角色的变化赋予算法在两阶段寻优中具备不同的侧重点。算法的第一阶段侧重全局探索，第二阶段侧重局部挖掘，如图1所示。

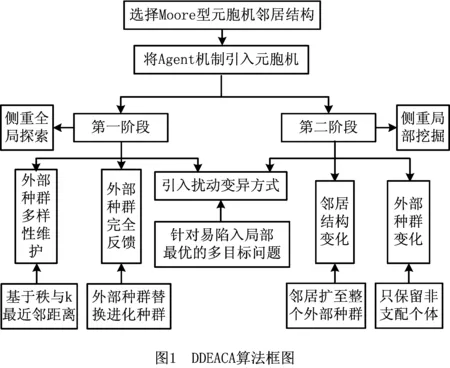
DDEACA算法的流程如图2所示，算法步骤如表1所示。

表1 算法步骤

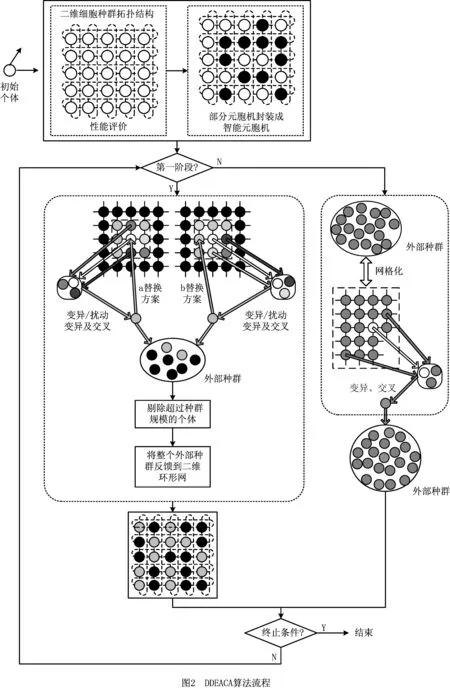
DDEACA算法伪代码如下：

1:population←create_Population() //创建初始种群

2:archive←create_Archive(population) //创建外部种群

3:while!terminationCondition()

4: if first-stage

5: for individual:1 to populationSize

6: neighborhood←get_Neighbours(population, position(individual));

7: parent1←select(neighbourhood);

8: parent2←select(neighbourhood);

9: while parent1=parent2

10: parent2←select(neighbourhood);

11: end while

12: offspring←DifferentialEvolution(individual, parent1, parent2);

13: evaluateFitness(offspring);

14: insert(position(individual), offspring, population);

15: add_Archive(individual); //加入外部种群

16: end for

17: population←replace_Individuals(population, archive); //反馈

18: else

19: if first gen of second-stage//第二阶段第一代

20: archive←change_Archive(archive)//外部种群保留非支配个体

21: end if

22: population←change_Population(archive) //外部种群作为进化种群

23: for individual:1 to populationSize

24: neighborhood←get_Neighbours(population, position(individual));

25: parent1←select(neighbourhood);

26: parent2←select(neighbourhood);

27: while parent1=parent2

28: parent2←select(neighbourhood);

29: end while

30: offspring←DifferentialEvolution(individual, parent1, parent2);

31: evaluateFitness(offspring);

32: add_Archive(individual); //加入外部种群

33: end for

34: end if

35:end while

2.1 算法第一阶段外部种群多样性维护

DDEACA算法的第一阶段外部种群多样性维护与NCellDE算法类似，首先对外部种群进行非支配排序，然后按表2中的规则对其进行维护筛选，设外部种群中秩为1的个体数量为a，外部种群规模为b，具体筛选过程如图3。

表2 外部种群多样性维护规则

2.2 算法第一阶段外部种群完全反馈

CellDE采用精英保留策略，其个体进入外部种群的标准非常严格。DDEACA算法在第一阶段进化时其外部种群需具备两方面功能：其一保留进化结束后的优良个体，其二收集当前进化过程中的优秀子代。在当代进化结束后，根据外部种群多样性维护规则进行处理，将剩余的所有个体作为下一代的父本，并将它们随机分配到二维环形网状结构中，如图4所示。

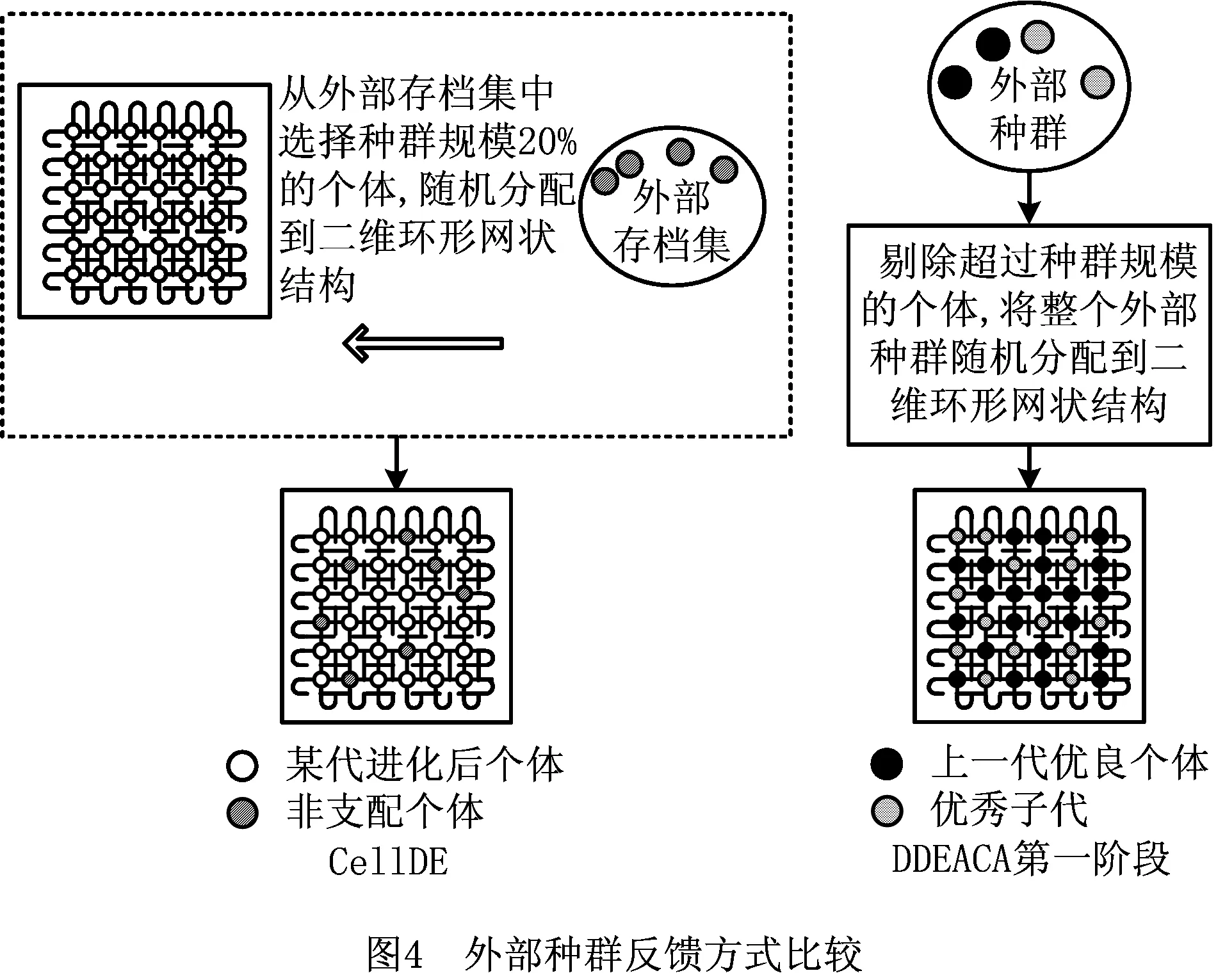
2.3 算法第二阶段外部种群和邻居结构变化

DDEACA在第二阶段进化时，外部种群的保留的不再是优秀个体，而是采取CellDE的外部种群保留策略，即外部种群只保留非支配个体，同时非支配个体的数目一旦超过外部种群规模，则立刻对外部种群进行修剪。与第一阶段不同，第二阶段下一代进化的种群实际上是上一代外部种群中保留的非支配个体。同时为了进一步调高算法的选择压力，加快算法的收敛速度。在第二阶段进化时，个体的邻居不再局限于局部范围，而是将整个外部种群中的其他个体都作为其邻居。如图5所示为外部种群和邻居结构变化的比较示意图。

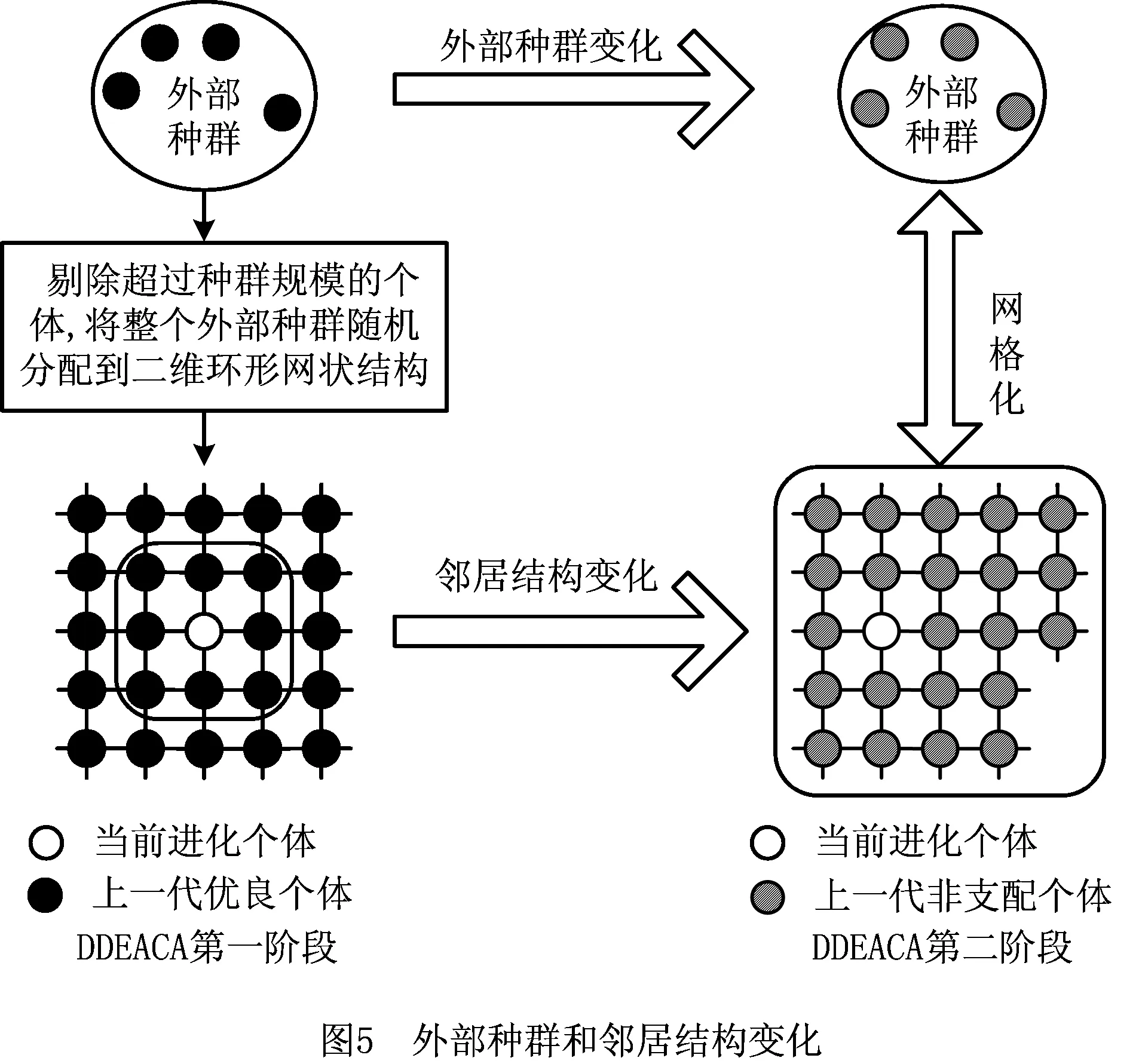
2.4 实验参数设置

在WFG系列问题上，将DDEACA同NSGA-Ⅱ、SPEA2、CellDE、NCellDE四种算法进行对比，考虑到运行时间等情况，其参数设置如表3所示。

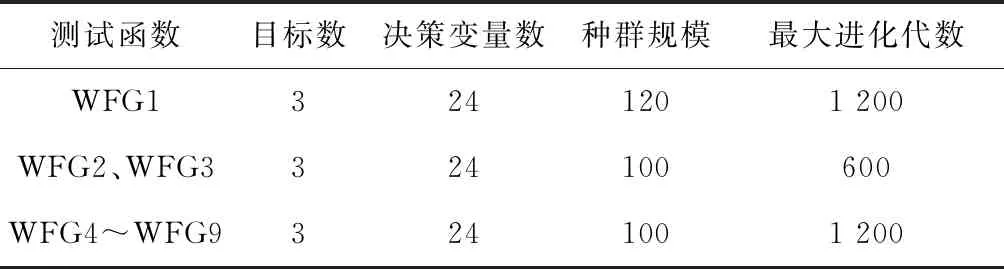
表3 实验参数设置表

NSGA-Ⅱ、SPEA2采用模拟二进制交叉，多项式

变异，交叉概率为0.9，变异概率为1/v(v为变量的个数)。在CellDE、NCellDE和DDEACA中，F=0.5，CR=0.1。每种算法独自运行50次。

2.5 DDEACA算法混合进化代数分配

DDEACA算法具有两阶段性，涉及第一阶段和第二阶段如何合理配置的问题，即第二阶段何时开始？本文以第二阶段与总进化代数的比值作为控制变量P，观察P对算法的性能影响和算法运行时间的影响。选取具有欺骗性和多峰的WFG9函数为测试函数(3个目标，24个决策变量)。DDEACA算法的运行参数如下：进化代数N=1 000，分别取缩放因子F=0.5、交叉因子CR=0.1，在不同的控制变量P下，算法运行15次。选取世代距离GD、超体积HV对算法性能进行分析评估。表4给出了实验结果。

表4 P对算法的性能影响

由表4的数据可知，当P值越大，即第二阶段占总进化代数时间越长时，算法的超体积越大，收敛性越好。但随着P值的增加，算法的运行时间也增加了。在算法能保持住多样性的前提下，算法收敛性的提高与算法第二阶段的运行最大进化代数的时间开销是矛盾的，综合考虑收敛性能和运行时间开销两个因素，取P=0.3，即最大进化代数的前0.7代为第一阶段，后0.3代为第二阶段。

3 基准函数测试

3.1 基准函数

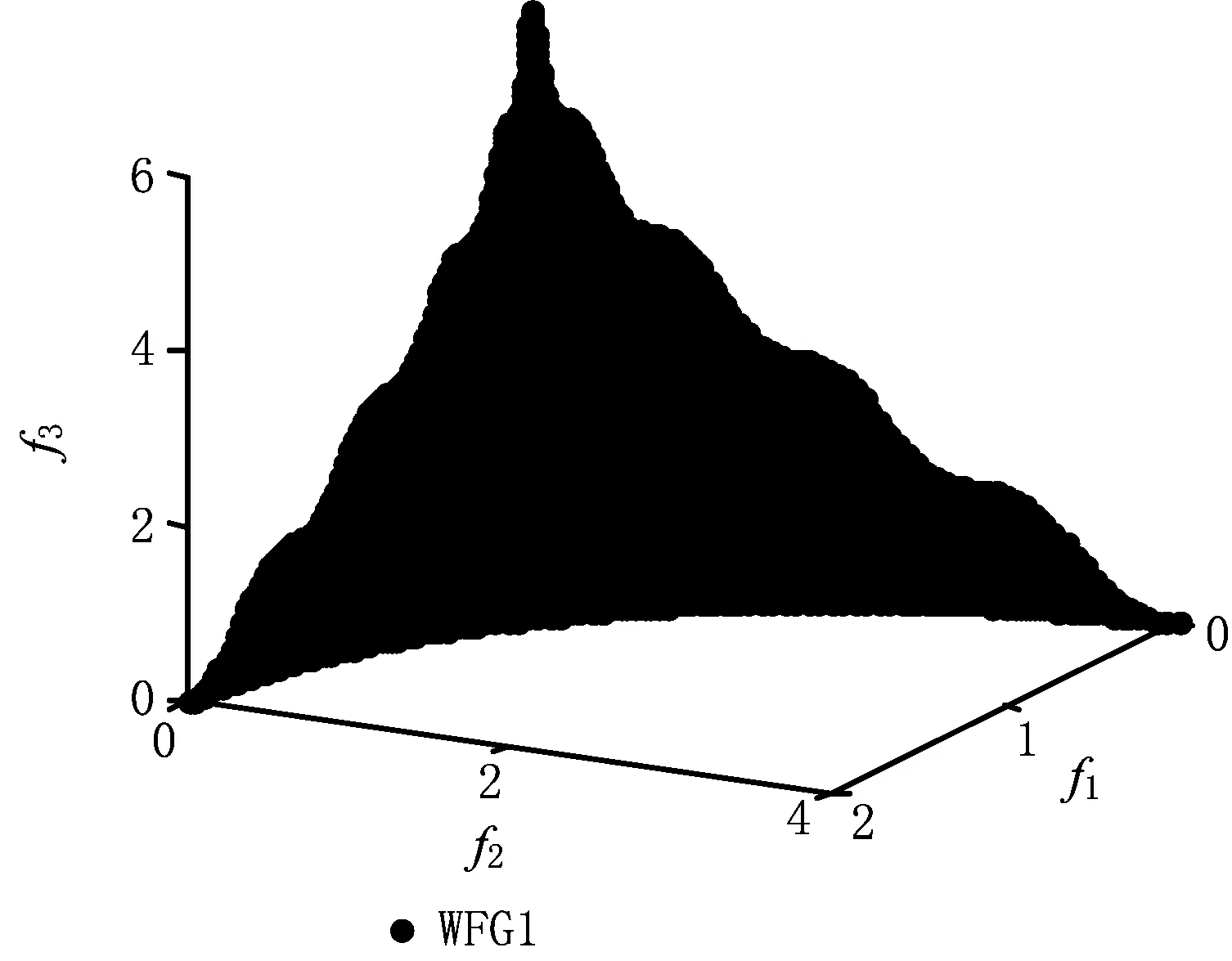
选择三目标的WFG系列函数对5种算法进行测试。WFG函数具有多峰性、偏好性、欺骗性和可分性等特性，其最优Pareto前端形状可以是凹/凸的、线性/非线性的、退化的及上述形状特征的组合[28-29]。WFG函数的特征如表5所示，其三目标Pareto最优边界如图6。

表5 测试函数特征

续表5

3.2 算法性能评价指标

性能度量指标如反向世代距离(Inverted Generational Distance, IGD)、ε[27]、世代距离(Generational Distance, GD)、分布指标(Spread, Δ)、超体积(Hypervolume, HV)[10]等。WFG函数由于最优前端幅值不等且部分问题的形状复杂[28]，本文采用GD和HV指标对算法性能进行测试分析。

(1)世代距离

世代距离是用来计算所得的Pareto前端收敛到最优Pareto前端的程度：

(3)

式中：n为近似Pareto前端中个体的数目，di为第i个解的目标函数构成的向量与Pareto最优前端之间的最近距离，GD大小与解的收敛性成反比。

(2)超体积

超体积用来计算获得的Pareto前端在目标空间所覆盖的体积：

(4)

超体积大小与Pareto前端的多样性、收敛性成线性关系。在三维目标空间中，vi是由参考点W与解i的目标向量作为对角点所形成的空间(长方体)的体积。

4 测试结果分析

4.1 算法性能测试及分析

表6和表7分别给出了4种算法关于GD、HV性能指标的统计结果(各个指标的最优值用深灰色标识，次优值用浅灰色标识)。表8和表9是DDEACA分别与其他3种算法两两之间的Mann-Whitney秩检验结果。原假设为性能指标的均值相等，显著性水平为0.05。

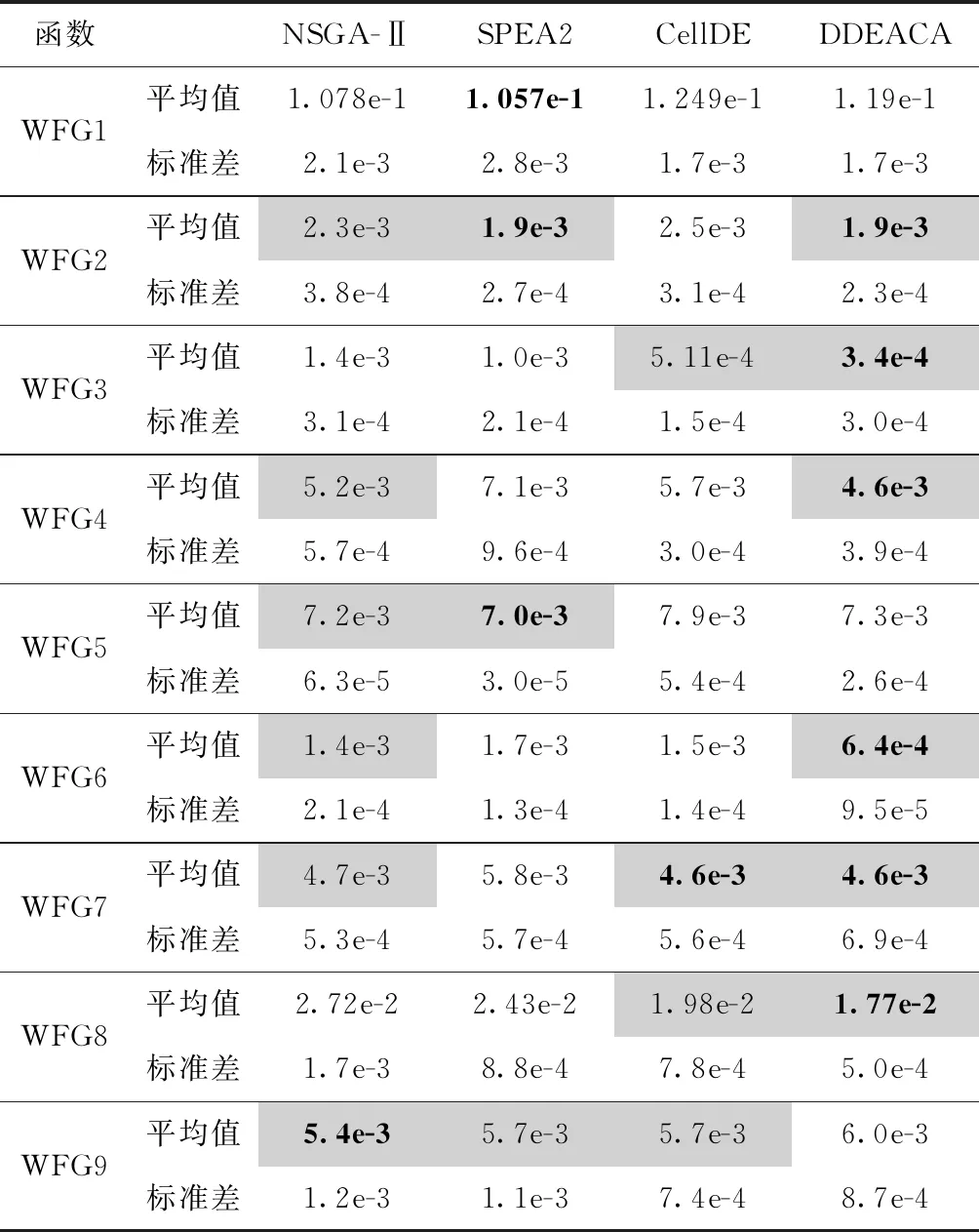
表6 收敛性指标GD

表7 覆盖性指标HV

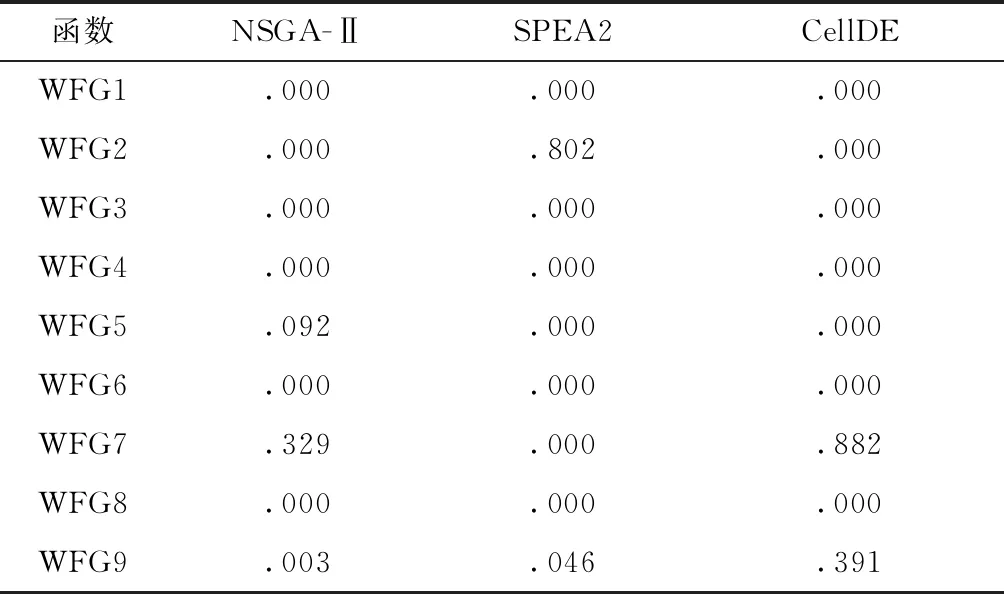
表8 GD指标Mann-Whitney检验

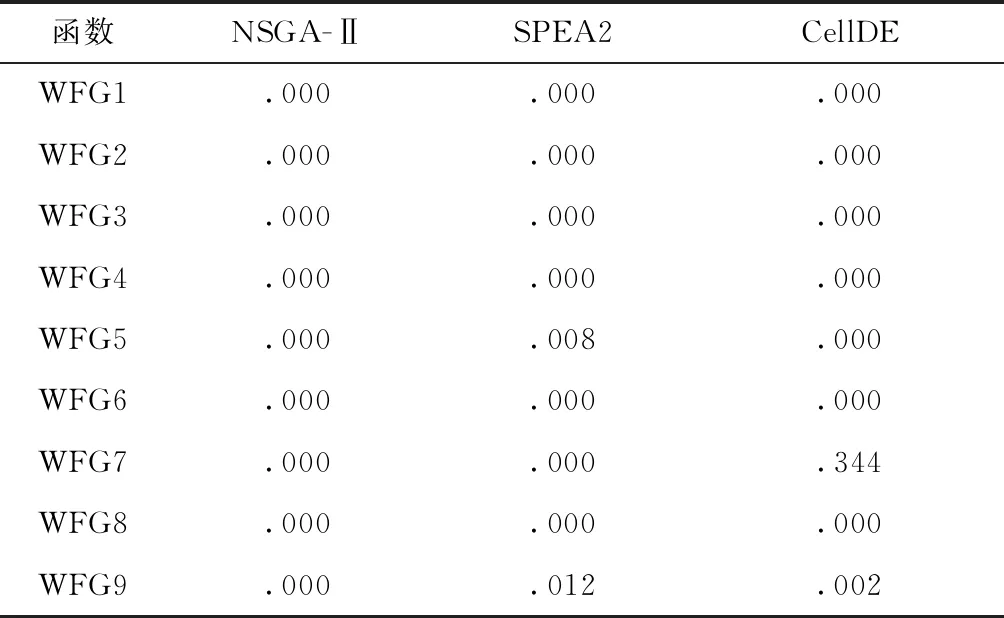
表9 HV指标Mann-Whitney检验

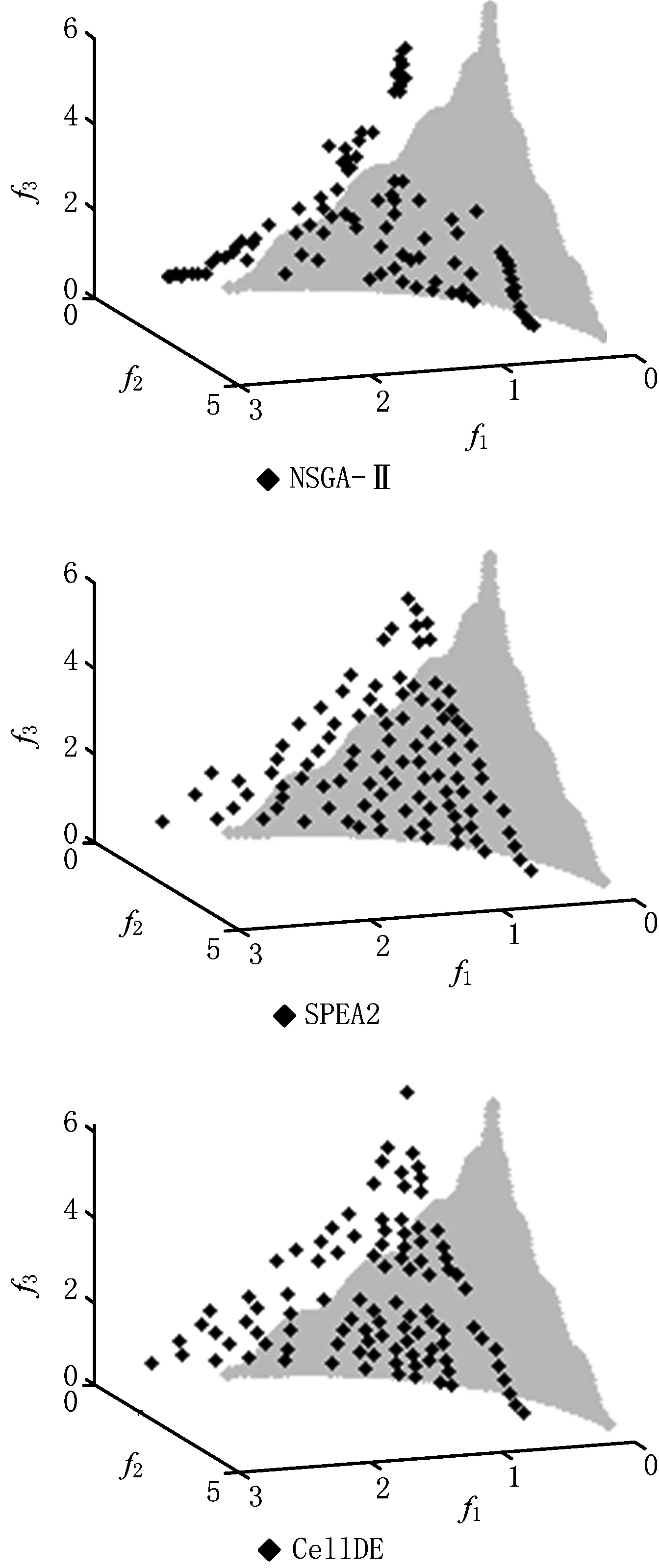
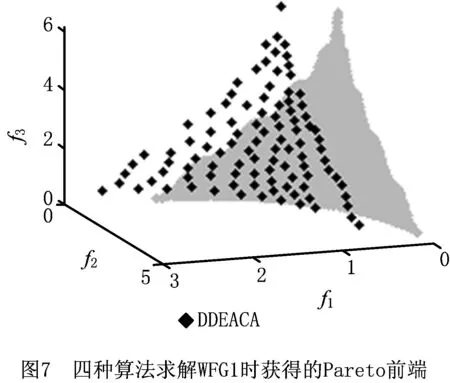
由表6的收敛性指标可知，DDEACA在WFG2～WFG4及WFG6～WFG8上取得了最优值，在WFG1、WFG5和WFG9上收敛性未获得最优值。同时由表8可知，DDEACA与其他3种对比算法在收敛性指标上存在显著差异。图7和图8分别给出了4种算法在WFG1、WFG2问题上获得的Pareto前端。DDEACA算法中的P值会影响算法的收敛性，在P=0.3时DDEACA在WFG1的收敛性不如NSGA-Ⅱ和SPEA2，但DDEACA获得的前端的多样性比较好。WFG1问题的最优Pareto前端由凹凸的曲面构成，DDEACA获得前端与最优前端有很好的一致性，而其他算法无法完全搜索出所有的凹面和凸面。另外，图8也证明了DDEACA能在求解时较好地保持前端多样性。WFG2的最优Pareto前端由断开的凹面构成，与其他算法相比，DDEACA获得的前端能较好地逼近所有凹面。

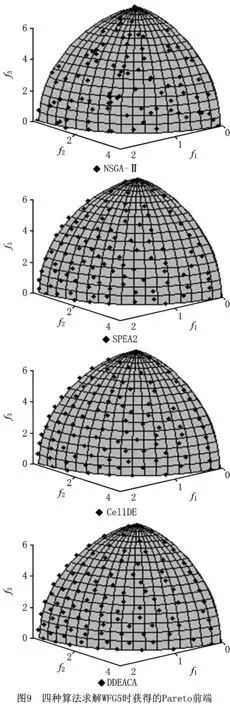
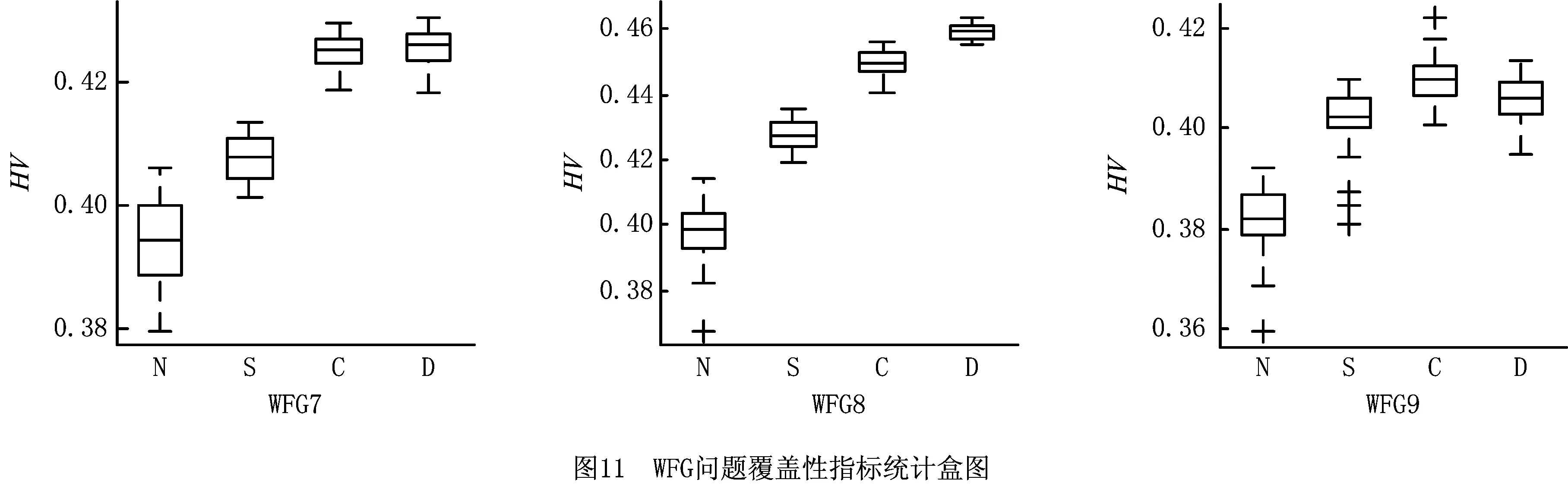
由表7的覆盖性指标可知，DDEACA在WFG2～WFG8上取得了最优值。同时由表9可知，除了WFG7问题外，DDEACA与其他对比算法在HV指标上存在显著差异。在WFG5问题上，尽管DDEACA的收敛性略逊色于NSGA-Ⅱ和SPEA2，但是DDEACA获得的前端多样性较好，其HV值优于NSGA-Ⅱ和SPEA2。图9给出了4种算法在WFG5问题上获得的Pareto前端，由图可知DDEACA获得的前端分布均匀性优于NSGA-Ⅱ和SPEA2。上述内容进一步证明了DDEACA对外部种群多样性维护方法的有效性。

4.2 WFG问题性能指标统计分析

图10和图11为4种算法在WFG问题上的性能指标统计盒图。在收敛性指标分布上，DDEACA算法在WFG3、WFG5、WFG7出现了超过两个异常值，在这些问题上，算法的稳定性稍差些，而在其余测试问题上，DDEACA具有较好的稳定性。

5 结束语

本文将智能体机制引入元胞种群并采用两阶段的外部种群多样性维护方法，将扰动因子引入变异操作避免陷入局部最优，提出一种外部种群充分引导的DDEACA算法。邻居结构和外部种群个体角色的变化可以调节算法的选择压力，可以较好地实现算法全局探索和局部寻优的平衡；第二阶段外部种群保留非支配个体可以减少算法对外部种群的维护时间开销。用WFG系列函数对算法进行测试和分析，验证了DDEACA算法的有效性，较好地兼顾全局搜索和局部寻优之间的协同问题，能获得更好的Pareto前端和竞争性的收敛结果。

本文仅对DDEACA算法本身进行了研究和测试，并对算法的两阶段性进行了探索和分析，未来将研究把算法应用于工程MOP，以期实现混合进化代数控制变量P与具体MOP问题的自适应调节，达到算法与MOP的协同优化。