基于多元统计方法的过程单元缓变故障识别

马方圆，林德溪，许明阳，王璟德，孙巍

（1北京化工大学化学工程学院，北京100029；2中化泉州石化有限公司，福建泉州362103）

随着自动化水平不断提高，化学工业生产运行中大量的测量数据可以被读取并存储在数据库中，使得利用多元统计学方法提取数据特征用于过程监测的想法得以应用[1-2]。目前，用于过程监测的多元统计学方法主要有主元分析法（principal component analysis，PCA）、偏最小二乘法（partial least square，PLS）、独立成分分析法（independent component analysis，ICA）等[3]。这些方法主要通过提取数据之间的相互关系来建立监测模型。其中PCA是常用的过程监测方法之一，通过监测当前装置运行状态与预设运行状态的偏差来实现对过程偏离的识别[4-5]。

在实际生产过程中存在着一些缓变的故障，在故障发生初期时偏离预设运行状态并不明显，不易被基于PCA 的过程监测模型识别出来。但这些缓变故障如果不被及时发现，不仅会导致产品质量的下降，影响企业的生产效益，甚至会导致生产安全事故的发生，威胁人员生命安全[6-7]。目前针对缓变故障的识别，主要是利用统计分析方法对数据信号进行处理，捕捉其相对于正常状态时的微小偏差[8-9]。例如，Mandal等[10-11]提出了一种基于时间序列的监测方法，通过计算试验信号与标准信号之间距离的经验累积分布函数来检测微小的故障信号，采用时间序列上的移动平均方法对信号的微小偏离实现时间上的累积；周媛等[12]利用基于相关时间规整算法，获取发动机在退化过程中的数据信息，提取其数据特征，实现对发动机状态变化的识别；赵修斌等[13]提出了一种基于BP 神经网络的缓变故障双阈值检测方法，利用BP 神经网络建立回归预测模型，在预测误差的基础上设置双阈值的低检测门限，可以实现对缓变故障发生初期微小变化的识别。这些方法均需要通过对系统的先验知识或足够的故障案例来实现对监测阈值的确定，但面对复杂系统或故障案例较少时则需要通过统计学方法计算出相应的监测指标。

孙美红等[14]提出了MCUSUM-PCA 方法，结合小波变换和累积和控制图（MCUSUM）的方法实现了对缓变故障信息的放大，在此基础上建立PCA模型，有效地改善了对缓变故障的监测效果；Bakdi 等[15]利用PCA 算法建立过程监测模型，通过基于修正的指数加权移动平均（exponentially weighted moving average, EWMA）控制图统计方法首先对统计量修正，开发了一种新的自适应阈值方法，该方法可有效地检测过程操作中的微小变化和突变；Harrou 等[16]利用PLS 算法作为建模框架，将对称化的Kullback-Leibler 距离作为检测异常情况的指标，通过计算无故障数据和故障数据概率密度函数之间的不相似性，实现对故障的早期识别，相较于传统的基于PLS的过程监测方法，对缓变故障具有更高的灵敏性和有效性。但这些方法计算复杂，且模型需提前设置众多参数，特别是机理过程不明时，这些参数很难被准确确定，因此应用于化工生产过程中较为困难。

受以上方法的启发，假设能够放大装置发生故障时与预设状态之间的偏差，则应该可以更好地实现对缓变故障的识别。当装置平稳运行时，变量之间的相互关系是固定的，一旦发生故障，这种关系也会随之发生改变。此时使用原有的变量间的回归关系预测某个变量，其预测值与实测值误差则会很大。同时由于发生故障时每个变量本身均有微小的偏离，将其代入回归模型中会进一步放大预测值与实测值之间的误差。如果在此基础上建立过程监测模型，则应该能够更好地实现对缓变故障的识别。PLS是一种常用于高维数据降维回归的方法，利用PLS 提取了变量之间的互相关关系建立回归模型，计算预测值与实际值之间的差值，实现了将装置偏离正常工况的程度定量化。同时，经过PLS预处理后正常工况的数据分布范围更小，更有利于发现缓变故障早期时的微小偏离。PCA是一种常用的高维数据降维方法，结合T2统计量可以较为容易地获取监测指标，用来判断装置的运行状态是否偏离正常工况。在经PLS预处理后的数据基础上建立PCA模型，相当于变量之间的互相关关系进行了二次挖掘，进一步正交了监测模型对变量间关系变化的敏感性，可以更好地实现对缓变故障的早期识别。同时，相比于文献中所提到的方法，将偏最小二乘法和主元分析法相融合，建立相应的过程监测模型过程更简单，监测指标易于获取且所需选择的参数较少，更易于应用在工业实际生产过程中。

本文在PCA 模型的基础上提出了PLS-PCA 模型，利用PLS算法提取过程变量之间的关系，获取装置运行状态与预设状态间的偏差，在此基础上建立PCA 模型，连续两次提取变量之间的互相关关系，进一步放大缓变故障的偏离程度，以实现对缓变故障的有效识别。该方法被应用于某石化企业制氢装置预转化反应器的过程监测中，用于对缓变故障的早期识别。

1 PCA及PLS算法

PCA 及PLS 是两种常见的过程监测方法。其中，PCA是一种广泛使用的数据降维方法，通过多元投影的方式将高维数据经过线性变化后投影在相互正交的新空间内，实现了对高维数据的降维处理。后经过美国数理统计学家Hotelling的改进，被广泛应用于化工生产过程中的过程监测与故障诊断[17]。PLS 是一种常用的多元线性回归方法，被应用于许多领域的回归计算，该方法通过提取变量间的潜变量，实现对高维数据的降维回归，且可以有效去除变量之间的共线性[18]。

1.1 PCA

选取生产过程中正常运行的历史数据X ∈R(n×m)，其中n为样本数，m为变量数。其协方差矩阵可由式(1)得到。

通过对原始矩阵X的分解，可以将原始矩阵写成载荷矩阵pi和得分矩阵ti的乘积再加上残差矩阵E的形式，如式(2)所示。

式中，k为PCA模型的主元个数，可以通过累计方差贡献率法（cumulative percent variance,CPV）、PRESS检验法和交叉验证法等方法来确定。建立了PCA 监测模型后，可以利用T2统计量及其控制限来判断生产过程是否偏离正常的运行状态。T2统计量的计算如式(3)。

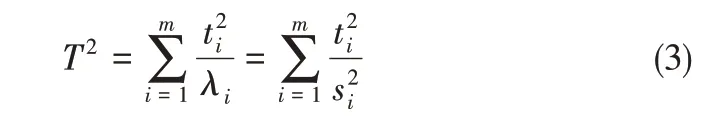
式中，λi为特征值；为ti的方差。

1.2 PLS

偏最小二乘法与主元分析法有许多相同点，也可以很好地解决变量间的相关性问题，实现对高维数据的降维回归，同时最大限度地保证自变量空间的数据特征对因变量的解释作用。其实现过程如下，假设自变量X ∈R(n×m)及因变量Y ∈R(n×p)为经过标准化处理后的数据矩阵，PLS通过提取变量的潜变量，并建立X和Y之间的有偏回归模型。矩阵X和Y可以分别分解如式(4)和式(5)。

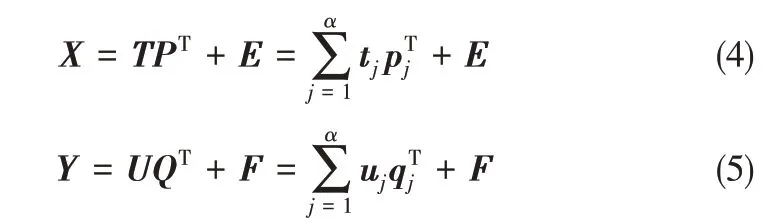
式中，T和U为得分矩阵；P和Q为载荷矩阵；α为潜变量的个数；E和F为残差矩阵；ti和ui为得分向量；pi和qi为载荷向量。

由线性估计可获得ti和ui之间的关系，其关系如式(6)所示。

式中，bi为回归系数。在PLS模型中，潜变量的个数是一个十分重要的参数，可以通过交叉验证的方法来选取最优的潜变量个数。残差标准误差（residual standard error，RSE）是评价线性回归拟合效果的一个常用指标，被认为是建立的模型与数据不匹配的度量[19]，其计算如式(7)所示。

式中，yi表示真实值；ŷi表示模型的预测价值。RSE值越小，说明模型的拟合效果越好。

2 基于PLS-PCA过程监测方法

在实际化工生产过程中，装置平稳运行可视为装置的预设状态。当装置处于平稳运行状态时，变量之间的关系是相对稳定的，因此可以利用PLS算法提取变量之间的关系，实现利用一部分变量回归其余变量。当装置处于平稳状态时，回归值与实际值之间的偏差应是均值为零，近于正态分布的数值较小的随机值；而过程出现异常时，尽管该偏差数值较小，但会呈持续大于或小于零的状态，是过程偏离及随机波动的叠加。

本文在PLS算法和PCA算法的基础上构建了一个PLS-PCA 模型，用于实现对化工生产过程中缓变故障的识别。如图1所示，首先选取一段装置平稳运行的过程数据作为PLS模型的训练数据，针对每一个过程变量，依次提取其与剩余变量之间的回归关系，分别建立PLS模型。利用所建立的各PLS回归模型，可获取假设装置处于平稳运行状态时各变量的预设值。

在建立PLS回归模型的基础上，选取另一段装置平稳运行的数据作为PCA 模型的训练数据，将其输入至各PLS回归模型中进行预处理，获取装置各变量的预设值Yipre。通过计算变量实测值与预测值之间的误差，获取各变量相对于正常工况时的偏离程度ΔY，然后在偏离值ΔY的基础上建立PCA过程监测模型，至此基于PLS-PCA 的过程监测模型建立完成。在运用于实际生产过程的监测时，实时数据首先通过PLS回归模型后计算出其与正常工况时的偏差，再将偏差值输入PCA过程监测模型中，从而实现对生产过程的实时监测。

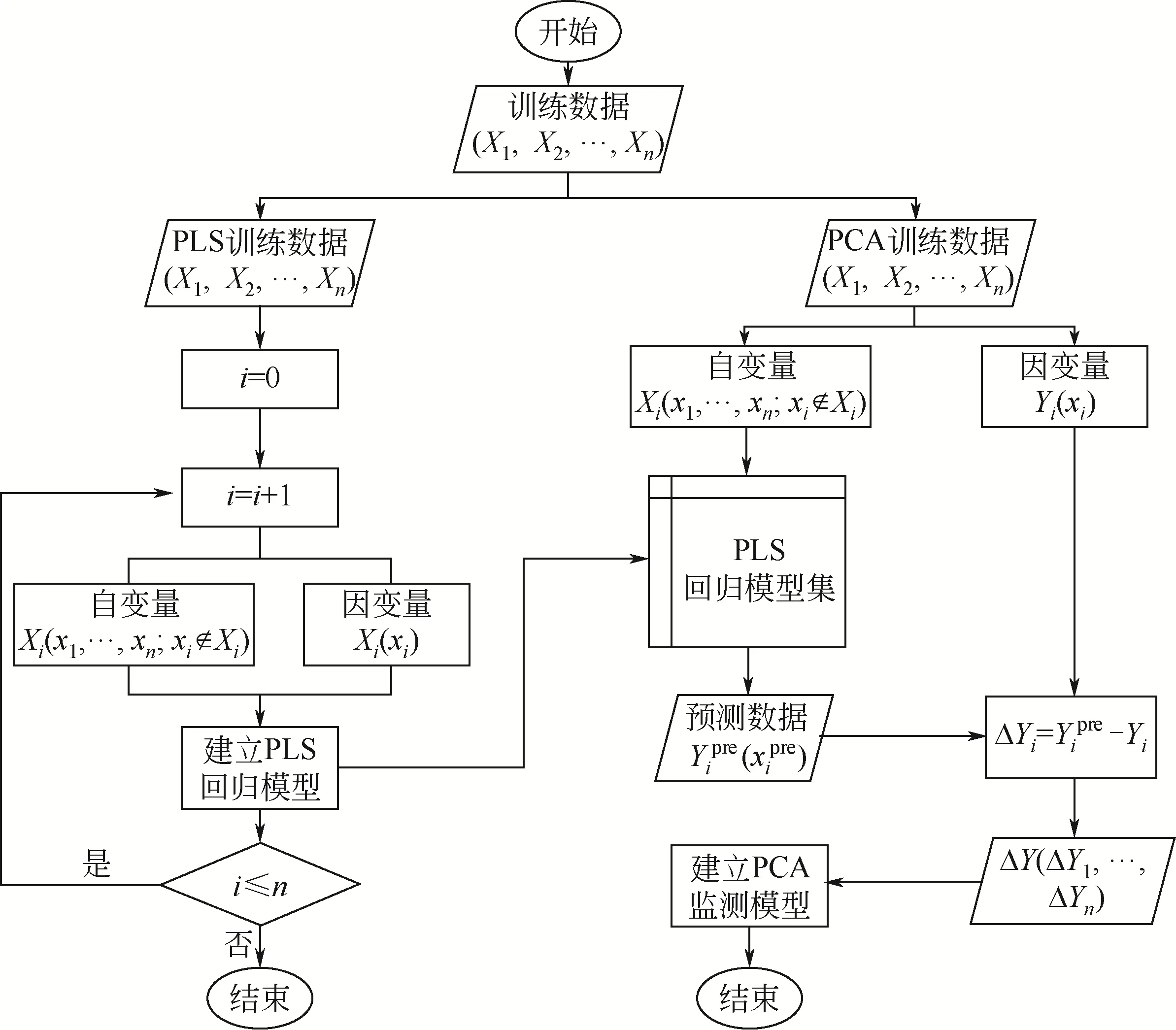
图1 算法逻辑框图

3 案例分析

3.1 数据采集

本研究所使用的数据均来自于某石化企业制氢装置预转化反应器的实际生产数据。如图2 所示，该反应器为绝热式固定床反应器。原料气沿轴向自上而下流经反应床层，在固体催化剂的作用下，高分子烃类与稀释蒸汽发生预转化反应，生产富甲烷气体，从而降低了制氢转化炉的反应强度和热负荷。

图2 预转化反应器床层测温点分布图

在化工生产过程中，设备不同位置的组分、温度和压力数据可以直接或间接反映出反应的进程。其中组分数据是对反应进程最直接的体现，而温度和压力数据则反映了反应的结果。如果能够实时获取组分数据，则可以实现对反应进程的直接监测。但在实际生产过程中，获取组分数据较为困难，相比于组分数据，温度和压力数据则更容易实现实时获取。因此，工程师主要利用温度和压力数据来间接判断反应的进程。

本文主要收集了该预转化反应器的床层温度数据用于实现对缓变故障的过程监测。该预转化反应器温度测量点的空间分布情况如图2所示，18个温度测量点分布在6个不同的床层高度上，每个床层高度各有3个温度测量点。本文收集了该反应器某年10 月1 日至12 月31 日共132480 组床层温度数据，其时间间隔为1min。

3.2 模型构建

根据前文中所提出的构建基于PLS-PCA 的过程监测模型方法，首先选取了一段装置平稳运行的生产过程数据，针对每一个床层温度变量，分别建立了相应的PLS 回归模型，利用其余17 个床层温度变量实现了对该温度数据的回归预测。在建立PLS回归模型的过程中，潜变量个数是一个重要的参数。表1 为根据交叉验证的方法，选取了18 个PLS回归模型的潜变量个数。

在建立PLS回归模型的基础上，选取一段运行平稳的数据代入到PLS回归模型中，并计算出装置正常运行状态时与预设状态之间的差值，并将其作为PCA 模块的训练数据建立基于PCA 的过程监测模型，PCA模型的主元个数通过累计方差贡献率法确定，如图3所示当主元个数为15时，PCA模型的累计方差贡献率超过90%，说明此时主元模型提取数据信息包含绝大多数的历史数据信息，因此选择模型的主元个数为15。在完成以上工作后，基于PLS-PCA 的过程监测模型建立完成，然后将测试数据首先代入PLS回归模型中，计算各变量与预设状态的偏差，再将其代入PCA 模型中实现对生产过程的监测。

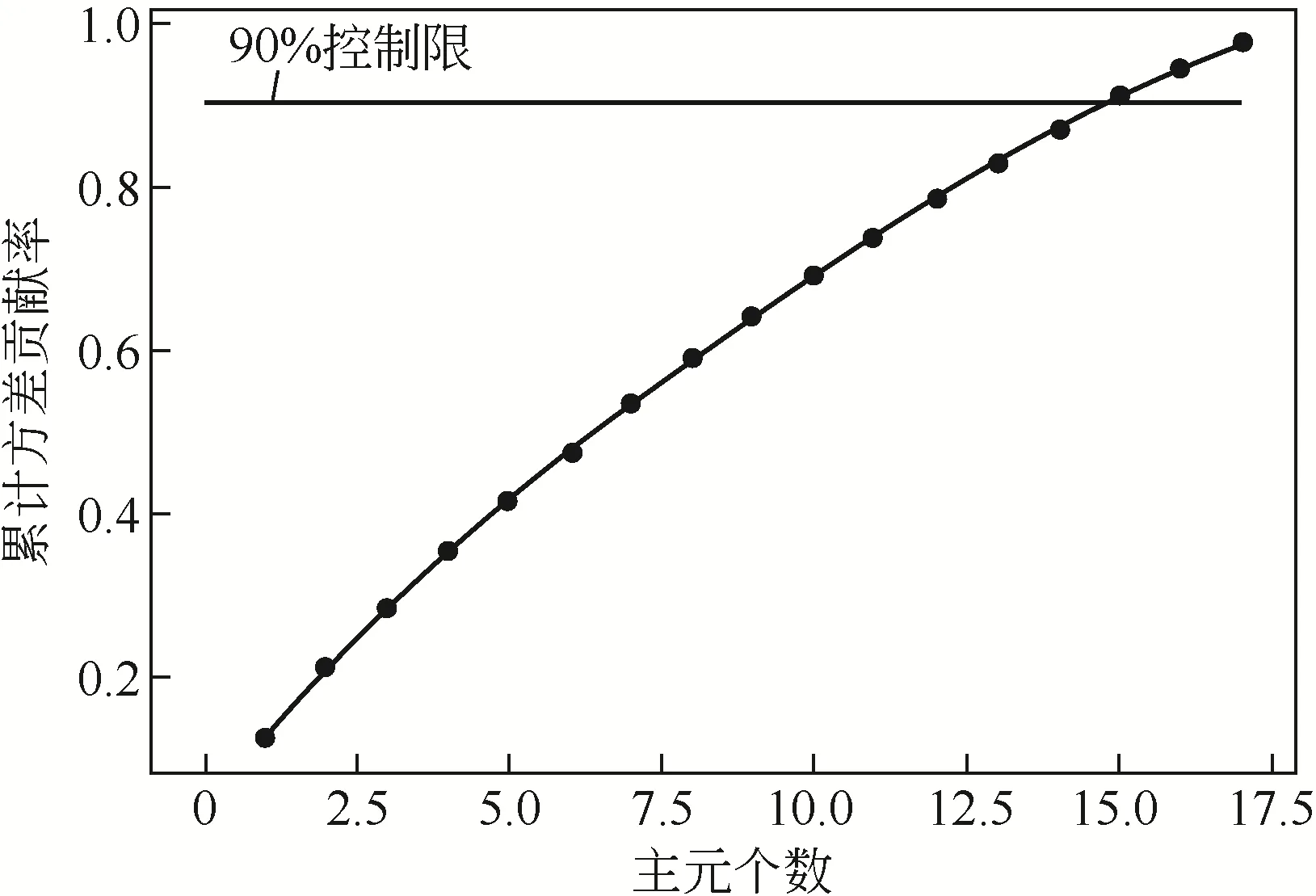
图3 信息提取量变化图

3.3 结果与讨论

将上文中已建立的基于PLS-PCA 的过程监测模型应用于该预转化反应器的运行状态监测中，监测结果如图4所示。其超限时间点为2016年11月9日15 时35 分。通过查询装置历史记录得知，工程师在2016 年11 月10 日4 时20 分发现床层C、D 点温度下降，后经分析发现稀释蒸气中硫含量超标，导致预转化催化剂硫中毒，从而引发了过程偏离。由此看出模型对缓变故障具有较好的识别效果，可以比工程师提前13h发现过程偏离。

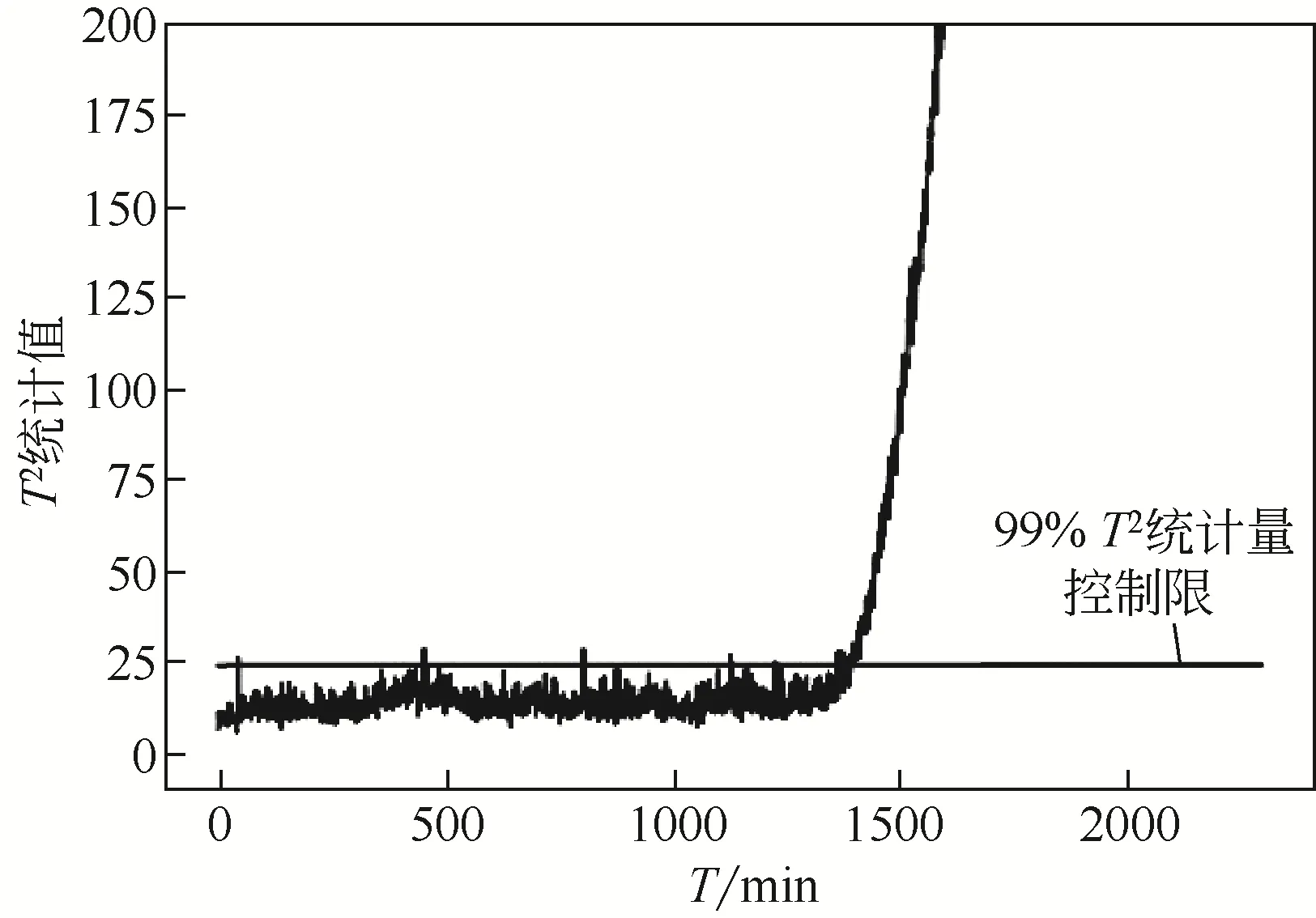
图4 基于PLS-PCA模型的过程监测结果

为了进一步与传统PCA 监测模型的性能进行比较，建立一个基于PCA 的过程监测模型并应于该装置的过程监测中，其监测结果如图5所示。其超限时间点为2016年11月9日23时48分。对比两种模型的监测结果可以发现，基于PLS-PCA 的过程监测模型要比基于PCA 的过程监测模型提前8h左右发现该过程偏离，说明基于PLS-PCA 的过程监测模型对于缓变故障具有更好的监测效果。

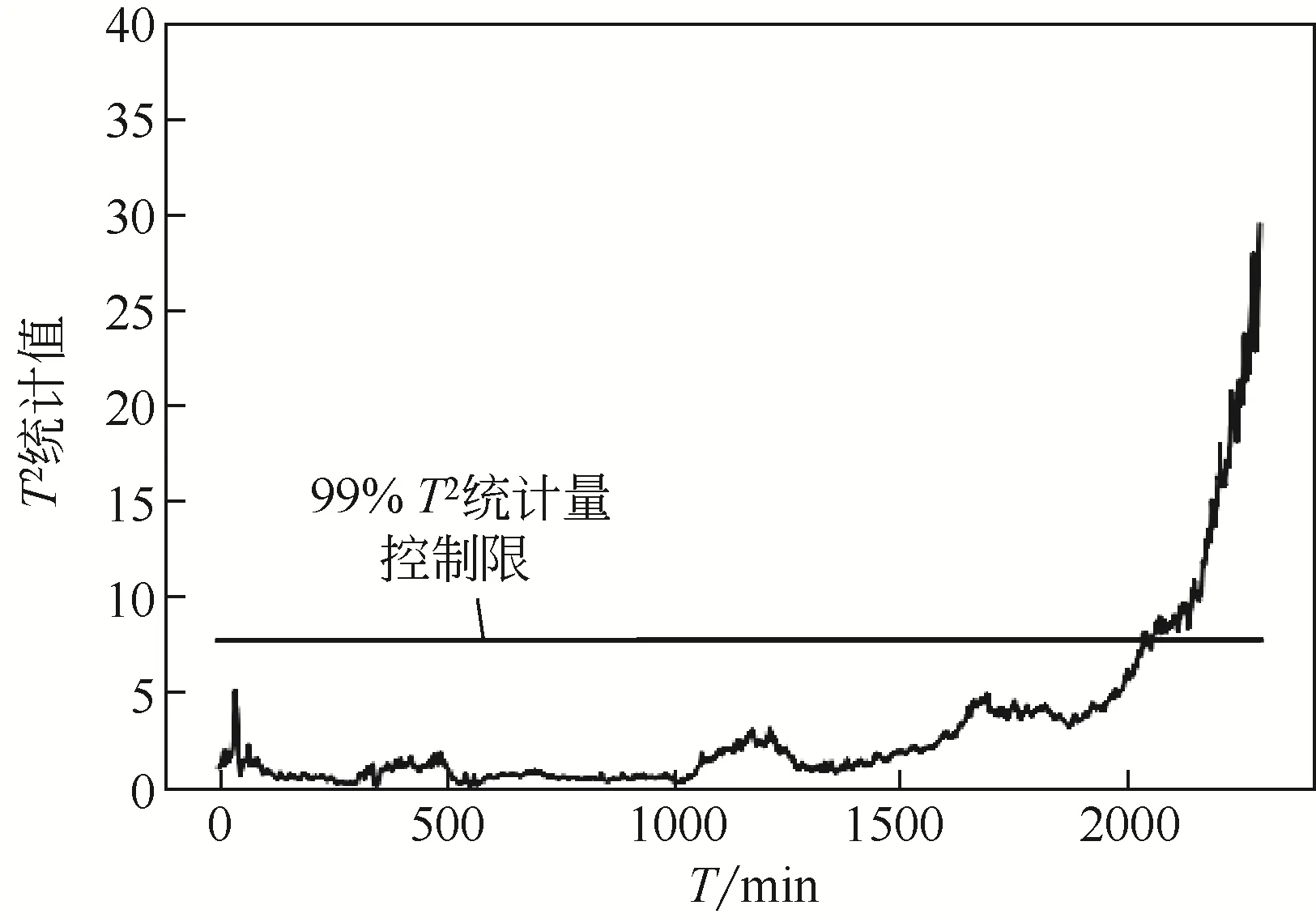
图5 基于PCA模型的过程监测结果

4 结论

本文针对化工生产过程中存在的缓变故障提出了一个基于PLS-PCA 的过程监测模型，利用PLS算法捕捉装置无故障状态下变量间的相关关系。在预测值与实测值偏差的基础上建立PCA 模型。当过程发生缓变故障时，该模型可以放大缓变故障的过程偏离，实现对缓变故障的早期识别。该模型被应用在某制氢装置的预转化反应器上，实现了对缓变故障的早期识别。结果表明，该模型能够比工程师提前13h发现过程偏离，对缓变故障具有较好的监测效果，其结果可以为工程师提供参考。