饱和氩气体热力学性质的分子动力学模拟
2020-05-08王宝和雷广平
王宝和 ,雷广平,2,王 维
(1.大连理工大学 化工学院,辽宁 大连 116024 ; 2.中北大学 机械与动力工程学院,山西 太原 030051 ; 3.大连理工大学 化工机械与安全学院,辽宁 大连 116024)
0 前言
众所周知,高压气体的热力学性质明显背离了理想气体,因此,高压气体的状态通常可以用逸度或逸度系数等热力学参数来描述。对于高压气-液平衡等过程,采用普通的实验方法难以实现,利用分子模拟的方法进行逸度或逸度系数的计算已经成为可能。MIZAN等[1]利用分子动力学(MD)模拟,研究了超临界水中过氧化氢自由基的逸度系数。WIERZCHOWSKI等[2]采用恒温恒压蒙特卡罗(MC)分子模拟法,研究了三种水模型的水蒸气逸度系数。本文拟采用分子动力学模拟技术,探讨了气-液平衡状态下饱和氩气体压力和逸度等热力学性质的计算。
1 模拟方法
1.1 模拟体系的建立
采用直角坐标系,模拟盒子如图1所示,液相位于模拟盒的中部,气相分别处于模拟盒的上下两侧,整个模拟体系中有两个气-液界面。对于氩流体,分子i和j间的相互作用势能函数U(rij)如式(1)所示[3]。
(1)
式中:rij为分子i和j之间的距离,ε为L-J能量参数,σ为L-J尺度参数。对于氩流体,σ=3.396 7×10-10m,ε=1.615 3×10-21J[3]。
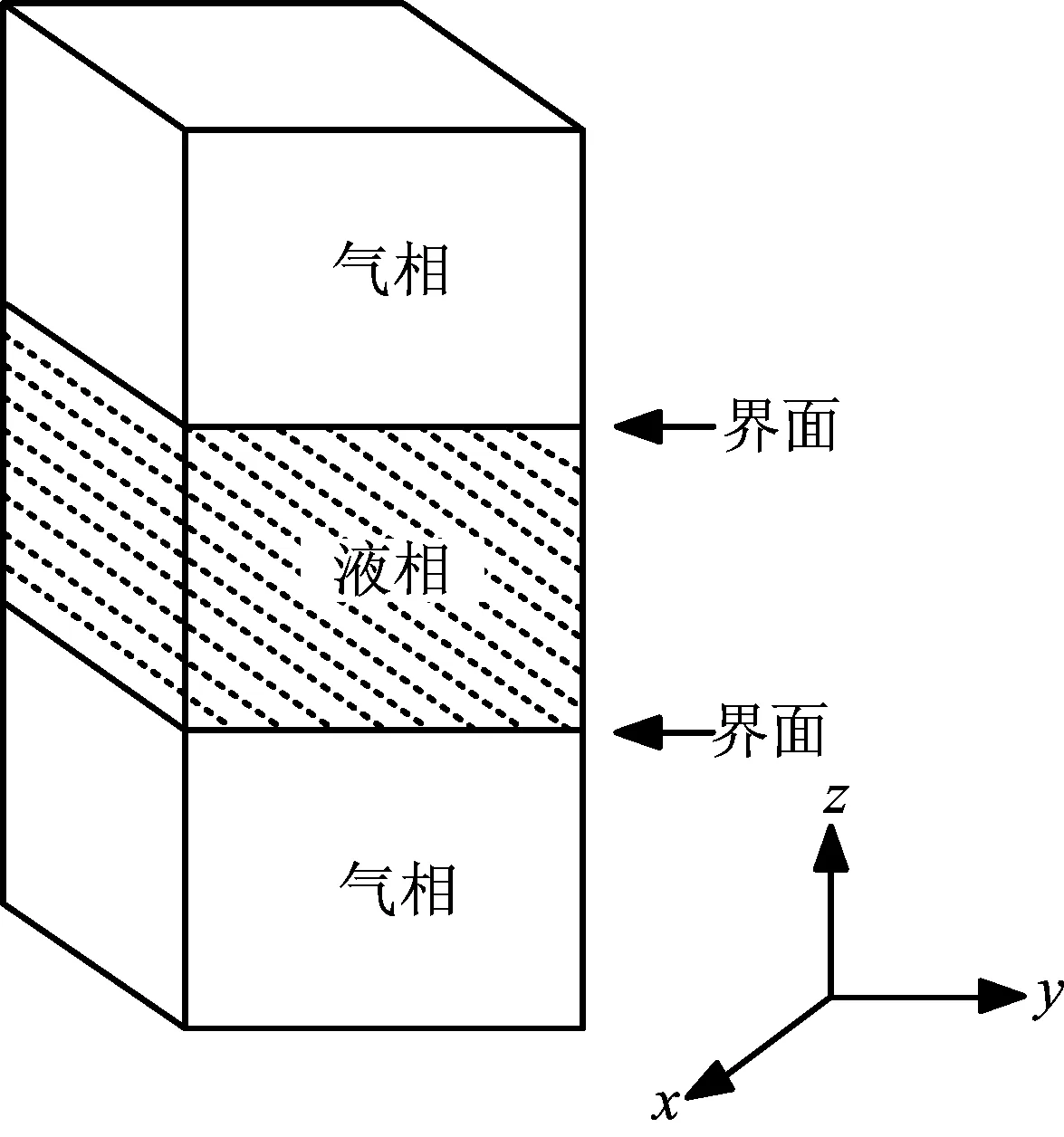
图1 模拟盒示意图
1.2 模拟细节
模拟体系由4 000个氩分子组成。初始时刻,饱和氩液体按照面心立方(FCC)方式排布于模拟盒子中部,上下两侧为真空区域,作为气相区。粒子初始速度随机给定。为使体系不发生宏观运动,模拟过程中不断调整质心位置及体系总动量,使质心位置处于坐标原点,体系总动量为零。截断半径rc=4σ(σ为氩分子的尺度参数)。时间步长Δt=4.331×10-15s,z方向划分300薄层用于统计密度分布。模拟中,x、y、z方向均采用周期性边界条件。系统采用NVT系综,采用Woodcock变标度法实现恒温控制,采用Velocity-Verlet法来求解牛顿运动方程。模拟过程共运算13万动力学步,前3万步用来实现气-液平衡。待系统平衡后,开始统计体系的热力学性质。本文所用模拟程序均为本课题组采用Fortran语言自行编写。算法流程如图2所示。
2 结果与讨论
2.1 饱和氩气体的摩尔体积
采用MD模拟方法,计算得到氩流体在不同温度和气-液平衡条件下,液相主体密度(ρL)、气相主体密度(ρG)及饱和氩气体的摩尔体积(Vm),如表1所示;密度分布曲线如图3所示。
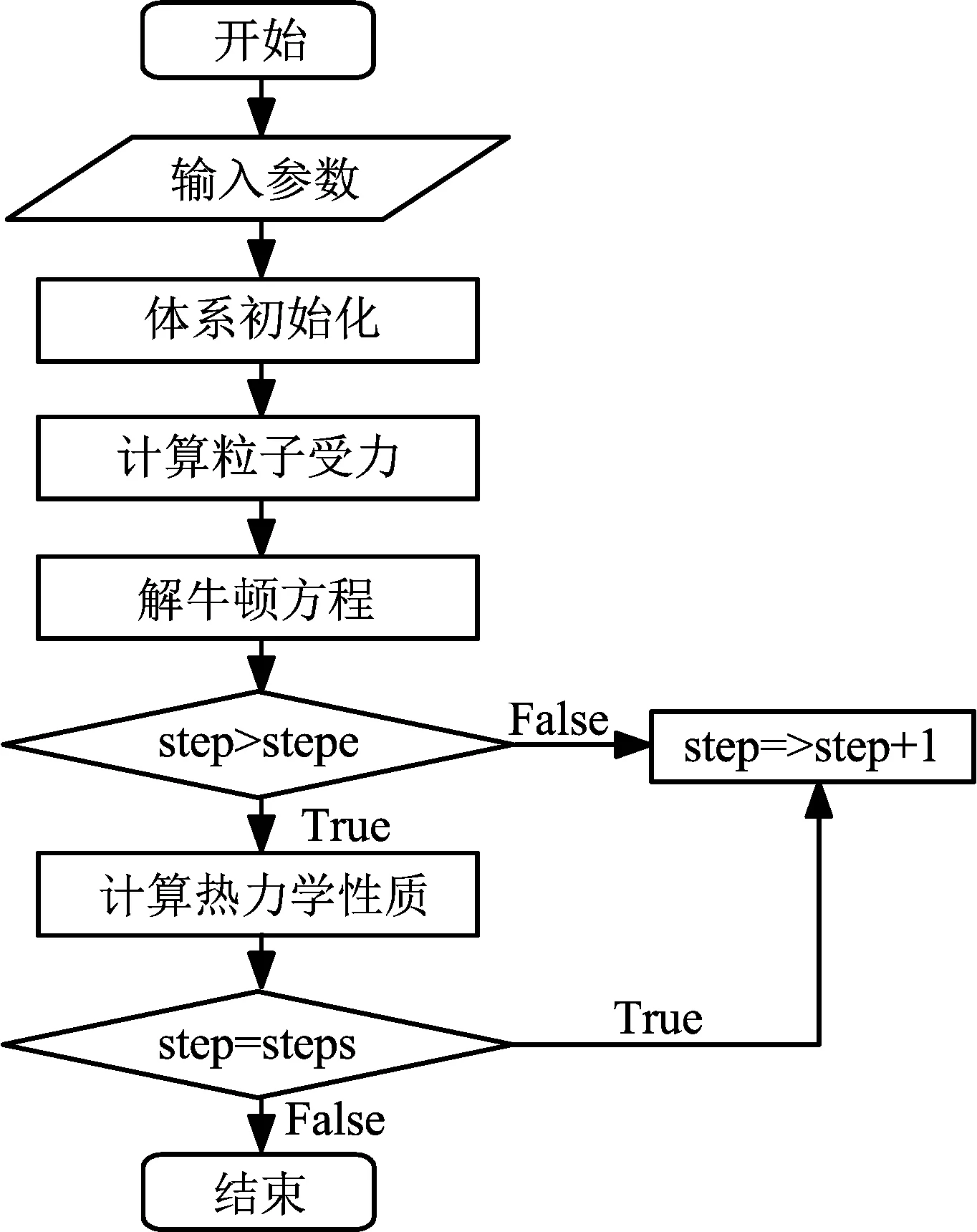
(注:stepe为平衡步数;steps为总运算步数)
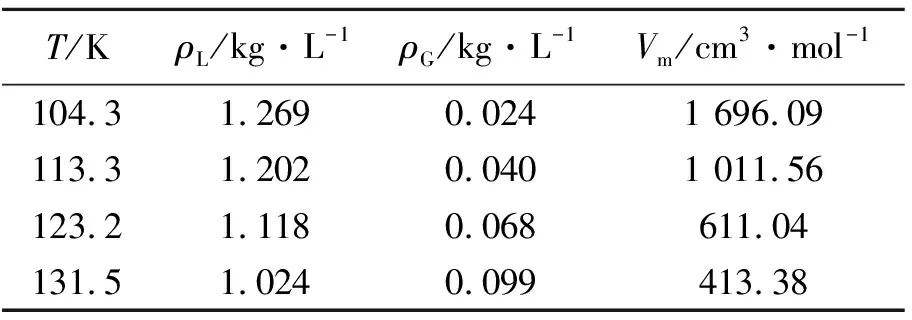
T/KρL/kg·L-1ρG/kg·L-1Vm/cm3·mol-1104.31.2690.0241 696.09113.31.2020.0401 011.56123.21.1180.068611.04131.51.0240.099413.38
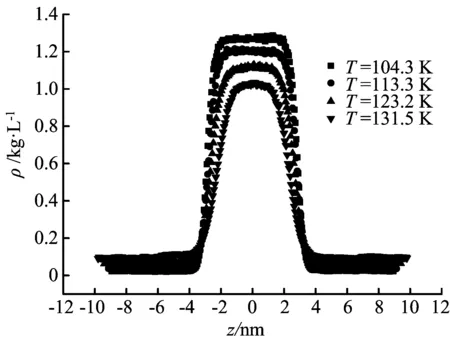
图3 不同温度下的密度分布曲线
由表1和图3可见,随着温度的升高,液相主体密度和饱和氩气体的摩尔体积逐渐降低,而汽相主体密度逐渐增大。
2.2 饱和氩气体压力的计算
2.2.1RK方程法
本文采用Ridlich-Kwang状态方程(2)(以下简称为RK方程)[4],来计算饱和氩气体的压力(pRK)。
(2)
式中:R为通用气体常数,T为温度,Vm为饱和氩气体的摩尔体积,a、b为参数,可根据流体的临界温度(Tc)和临界压力(pc),利用方程(3)计算得到[4]。
(3a)
b=0.086 64R2Tc/pc
(3b)
根据表1中饱和氩气体摩尔体积的MD模拟值,就可以利用方程(3)和(2),计算出不同温度下的饱和氩气体压力(pRK),如表2所示。
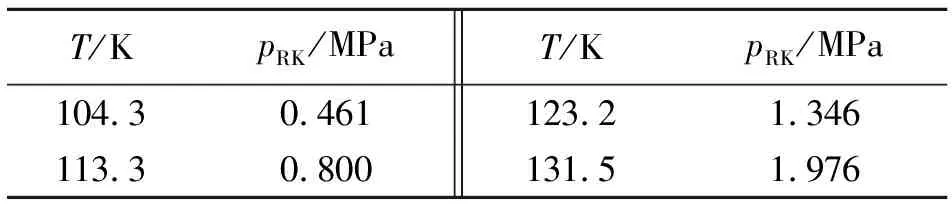
表2 不同温度下的pRK 值
2.2.2维里方程法
利用维里方程,采用分子动力学模拟的方法,计算得到不同温度下饱和氩气体压力(pMD,详细计算步骤参见文献),如表3所示[4]。
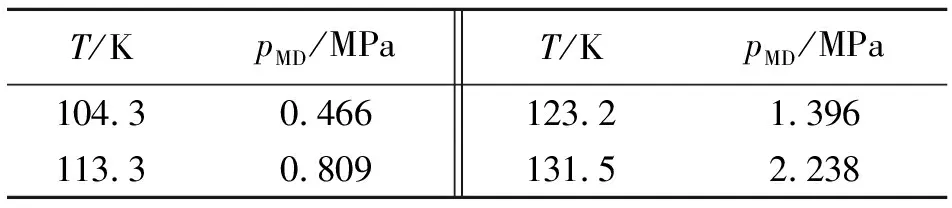
表3 不同温度下的pMD值
2.2.3两种方法计算结果的比较
在气-液平衡条件下,饱和氩气体压力的实验值(pexp),如表4所示[6]。
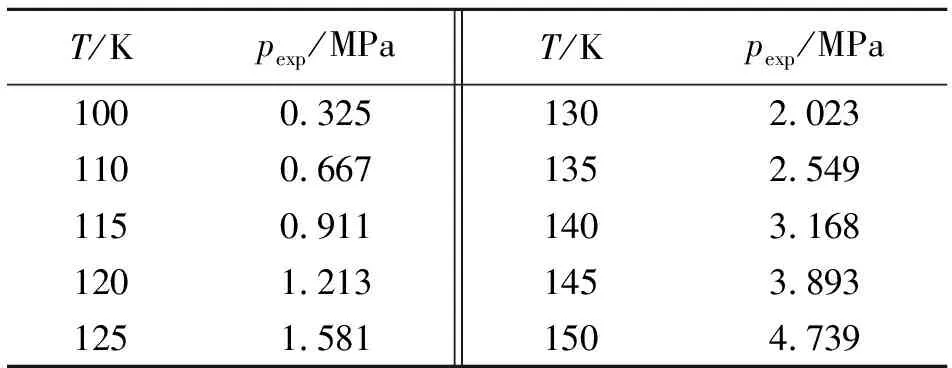
表4 不同温度下的pexp值
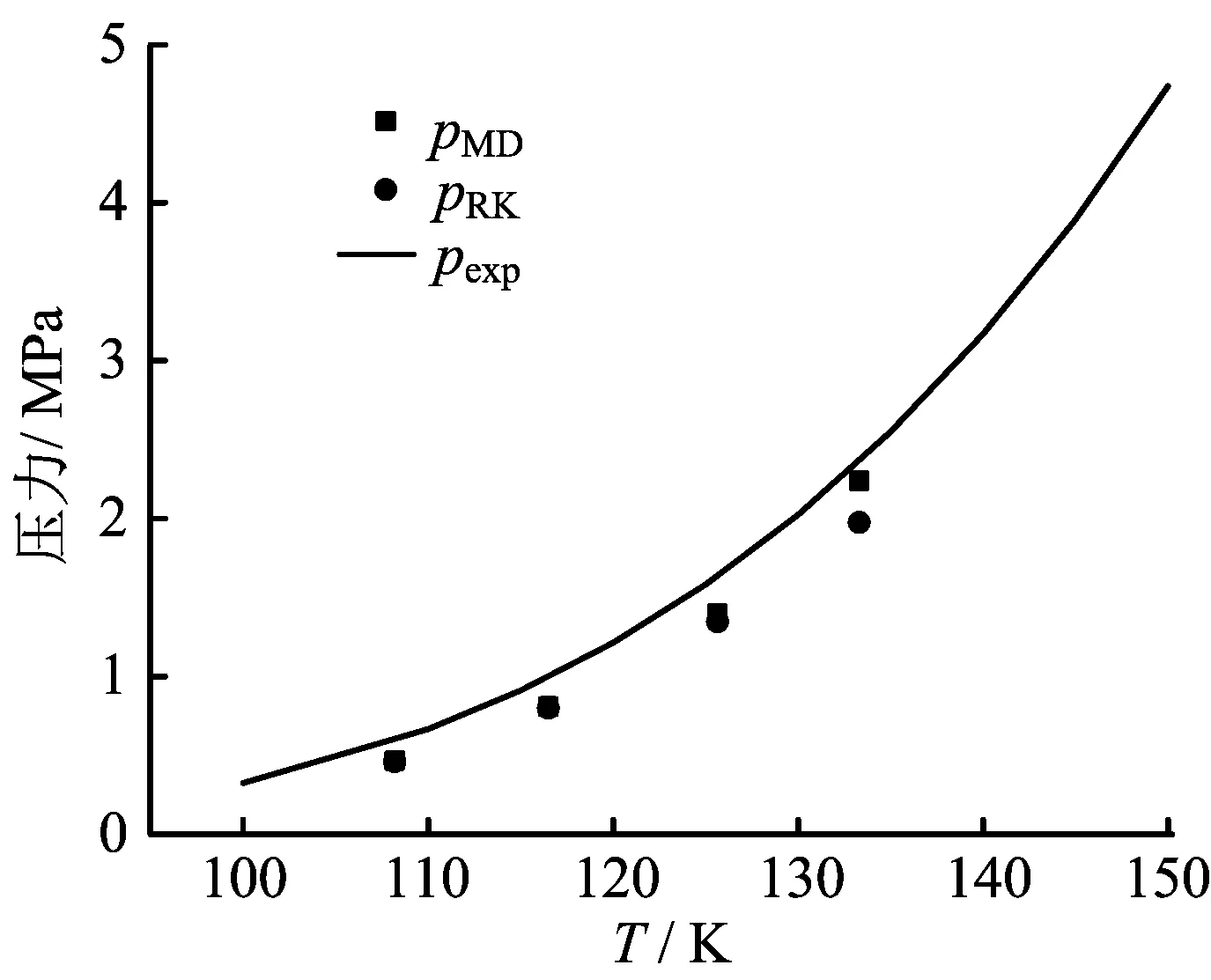
图4 不同方法计算得到的压力值比较
图4给出了不同方法得到的压力值的比较。可见,三种方法得到的饱和气体压力均随着温度的升高而增大。在整个模拟温度范围内,维里方程法及RK方程法得到的压力值均略低于实验值。在低温条件下,pMD与pRK比较接近;在高温条件下,pRK略小于pMD。整体而言,维里方程法计算得到的压力值更接近于实验值。
2.3 饱和氩气体逸度的计算
逸度的计算方法很多,既可以通过热力学数据计算获得,也可以通过气体状态方程计算得到。本文采用RK状态方程结合分子动力学模拟数据及实验数据,来计算饱和气体逸度(以下简称为RK方程法)。此外,本文还提出一种直接通过分子动力学模拟,来计算饱和气体逸度的新方法(以下简称为虚拟理想气体法)。
2.3.1RK方程法
在恒温条件下,纯组分逸度与pVT之间的关系,如方程(4)所示[6]。
(4)
式中:f为逸度,p为压力。将RK方程(2)代入方程(4),积分整理可以得方程(5)。
(5)
式中:Z为压缩因子,可利用方程(6)求得;Bp及A/B为参数,可由方程(7)计算得到。
pVm=ZRT
(6)
Bp=pb/RT
(7a)
A/B=a/bRT1.5
(7b)
由上述方程计算得到不同温度下的参数A/B、Bp及压缩因子Z值,如表5所示。可见,在气-液平衡条件下,饱和氩气体的压缩因子随温度的升高而降低,这说明随着温度的升高,饱和气体与理想气体的偏差会越来越大。
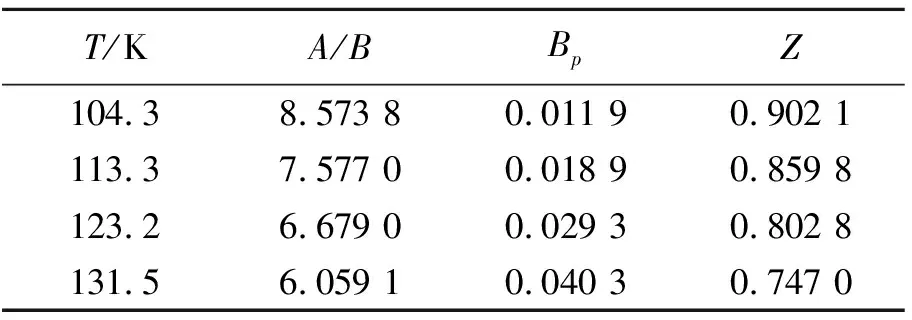
表5 不同温度下参数A/B、Bp及压缩因子Z值
根据表1的饱和氩气体的摩尔体积及表2的压力值,可以利用方程(5)和(6)求得不同温度下的逸度(fRK),如表6所示。为便于比较,表6还列出了相应温度下的压力值(pRK)。
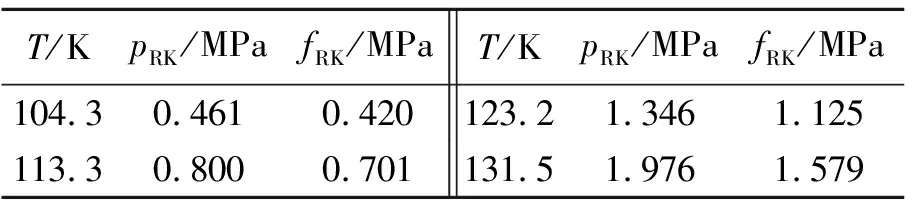
表6 不同温度下的pRK及fRK值
2.3.2虚拟理想气体法
本文提出一种直接利用分子动力学模拟,来计算饱和气体逸度的新方法,即:将饱和气体逸度看作是相同体积内含有的与饱和气体具有相同总能量的虚拟理想气体的压力。
众所周知,理想气体仅具有动能,即其总能量等于动能;而真实气体的总能量包括动能与势能。为将饱和气体转化为相同体积下的虚拟理想气体,本文将气体总能量看作理想气体分子运动的虚拟动能。则相同汽体体积中应含有的理想气体分子数(NV)可由式(8)来计算。
(8)
式中:Et为饱和气体总能量,Ek与Ep分别为饱和气体所具有的动能与势能,kB为波尔兹曼常数。
气体中理想气体的压力可根据理想气体状态方程计算,且该压力即视为饱和气体的逸度(fMD),如式(9)所示。
fMDV=NVkBT
(9)
式中:V为气体体积。
根据上述方程计算得到的不同温度下的饱和气体的动能(Ek)、势能(Ep)、气体体积(V)、气体分子数(N)、虚拟理想气体分子数(Nv),如表7所示。可见,随着温度的升高,气体中的分子数增大,这是由于温度升高分子获得更多动能,从而更容易挣脱液体对它的束缚而进入气相区。
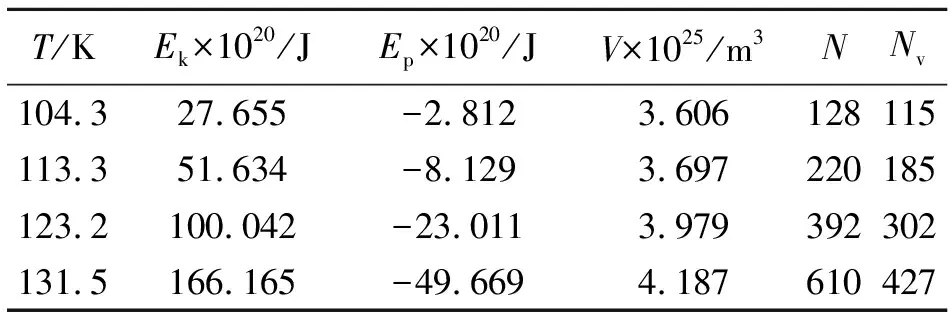
表7 不同温度下的气体动能、势能、气体体积、气体分子数及虚拟理想气体分子数
采用虚拟理想气体法计算得到的饱和气体逸度如表8所示。为便于比较,表8还列出了相应温度下的压力模拟值(pMD)。
根据方程(6)及(9),可以得到逸度系数、压缩因子及虚拟理想气体分子数之间的关系,如方程(10)所示。
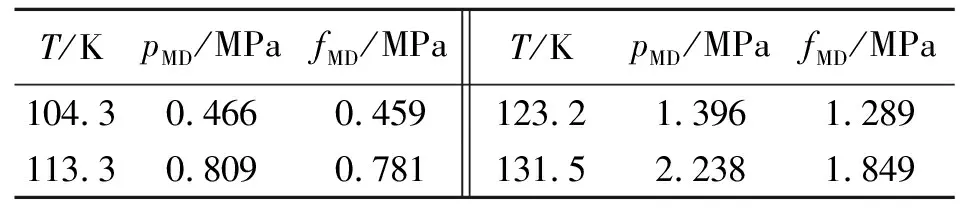
表8 不同温度下的pMD与fMD值
(10)
式中:φ为逸度系数。
根据表5及7可以计算得到Nv/(ZN)值,由表8可以计算出φ值,进而可以得到两者之间的相对误差,如表9所示。可见,随着温度的升高,Nv/(ZN)与逸度系数(φ)之间的相对误差逐渐增大。
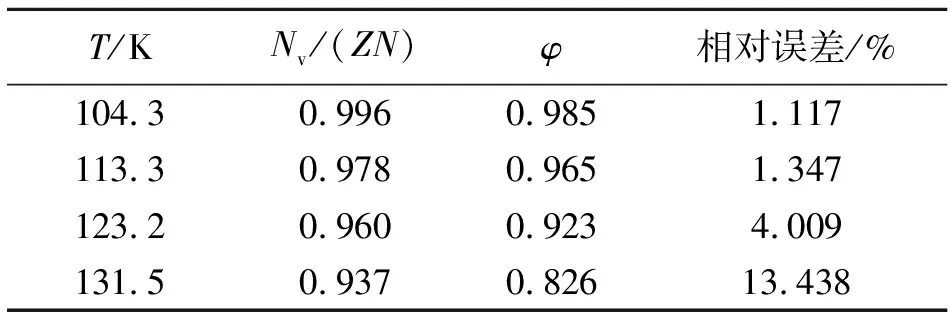
表9 不同温度下Nv/(ZN)、φ及两者相对误差
2.3.3不同方法计算结果的比较
将饱和气体压力实验值及摩尔体积实验值,利用方程(5)和(6)便可得到实验压力所对应的逸度(fexp)。不同温度下的fexp如表10所示。为便于比较,表10中还列出了相应温度下的压力模拟值pexp。
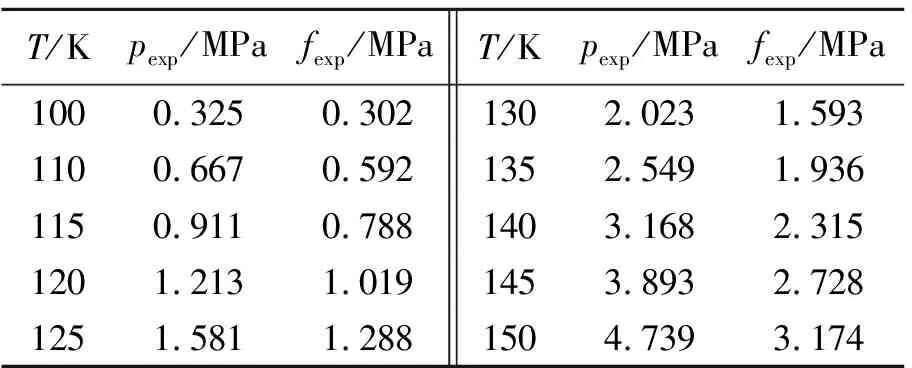
表10 不同温度下pexp与fexp值
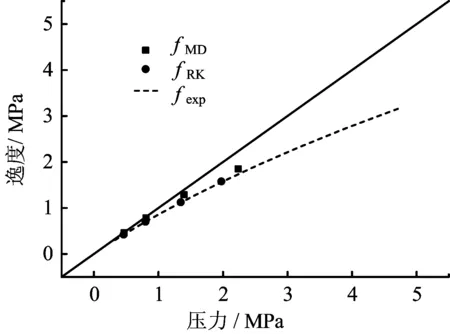
图5 不同方法所得逸度随饱和气体压力的变化曲线
图5给出了不同方法计算得到的逸度值与相应饱和气体压力的关系曲线。可见,随着饱和气体压力的升高,气体逸度与相应饱和压力的偏离程度增大,这说明随着温度的升高,饱和气体与理想气体偏离程度加大;在整个模拟范围内三种方法所得的逸度基本一致。虚拟理想气体法所得逸度fMD与fexp相比,其值稍微偏高,但相对误差在15%以内,而fRK与fexp则符合得更好,相对误差<5%。
3 结论
采用分子动力学模拟技术,对饱和氩气体的热力学性质进行了模拟计算,得到以下结论:①随着温度的升高,液相主体密度和饱和氩气体的摩尔体积逐渐降低,汽相主体密度逐渐增大。②维里方程法和RK方程法计算得到的饱和氩气体压力与实验值基本一致。③虚拟理想气体法及RK方程法计算得到的饱和氩气体逸度值及实验值三者基本一致。
