儿童视角·单元立意——“分数的初步认识”的整合设计与实践

□方苏云

分数与整数在意义、读写和计算方法上都有很大差异，分数的“量”“率”的含义，学生很难准确理解，这使得分数学习成为小学生较难掌握的一块内容。

一、透析现象，聚焦问题

在小学五、六年级分数学习中出现的高频率的“量”与“率”混淆不清的现象主要有以下这些。

（一）分数作为具体量的理解欠缺

从中可以看出，学生不习惯将分数作为具体量进行运用。如图1中，学生将分数转化成小数来计算；图2中，学生将“用去”当“率”来用，不理解这个分数表示的是具体量。

（二）分数的“量”“率”含义混淆

从图3、图4 的错误中可以看出，学生对分数“率”“量”的含义混淆不清。如何解决这一问题呢？笔者认为在初识分数时就要注重学生对分数“量”与“率”的理解。

二、审视教学，追溯根源

笔者对人教版教材中有关分数的内容进行了梳理，做了深入的解读分析，并借助前测分析学情，以此追根溯源。

（一）教材反观，明晰单元立意

1.分数教材的整体关联

三上“分数的初步认识”对后继五、六年级学习分数相关知识起着重要的奠基作用。整体关联可用下面的框架图表示。

“分数的初步认识”所有涉及的内容直接影响着五下的“分数的意义和性质”的教学；“分数的简单计算”中高频率地出现几分之一，为五下“分数的加法和减法”算理的理解和算法的掌握积累丰富的计算经验，是分数四则运算的“种子课”；“分数的简单应用”是《义务教育数学课程标准（2011 年版）》新增的内容，对“1”代表多个物体的理解及求一个数的几分之几的简单问题，实质就是六上分数乘、除法的雏形。

2.分数教材的具体分析

分析三上的“分数的初步认识”、五下的“分数的意义与加减法”、六上的“分数乘法除法”的例题素材，分数作为“量”与“率”意义的学习以明线的形式推进，整理如下：

学生在初次接触分数阶段，没有切入具体量的学习，这在很大程度上影响了学生对分数内涵的理解，也影响了学生用分数解决问题思路的形成。因此在初识分数时可以将具体量切入，多维度理解分数内涵。

（二）学情实证，立足儿童视角

笔者课前借助前测对学情进行了调查分析。

1.前测分析

笔者随机选取了本区的一所城镇小学，对该校三年级312名学生做了单元前测，内容包含分数含义、分数大小比较、分数加减法三个方面，对典型题进行了统计分析。

（1）分数作为“量”出现

正确人数统计分析：

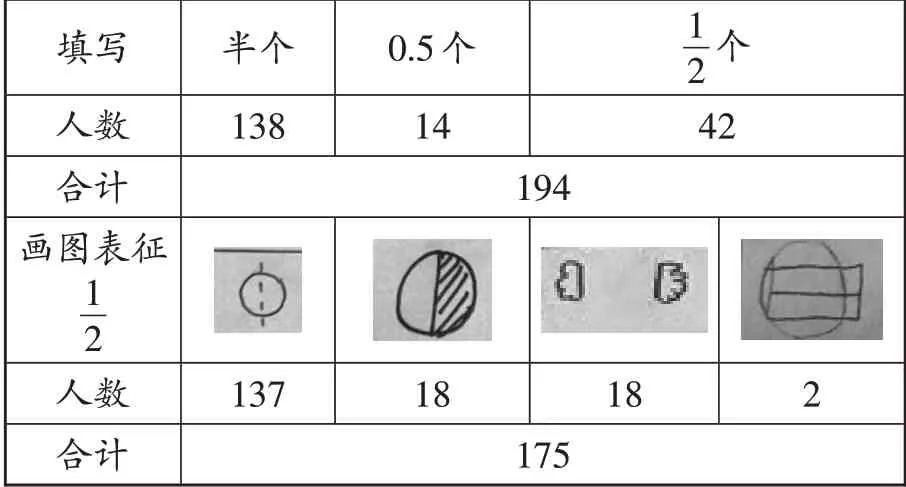
填写人数合计画图表征半个138 0.5个14 1 2 个42 194 1 2人数images/BZ_34_1482_2548_1570_2632.pngimages/BZ_34_1641_2539_1760_2641.pngimages/BZ_34_1810_2548_1975_2632.pngimages/BZ_34_2010_2540_2150_2640.png137 18 18 2合计175

从表中可以看出，62%的学生写出了正确答案：“半个”“0.5个”“个”，其中能用“个”表示结果的约占全部人数的13%；约有56%的学生能用图表示。由此可见，部分学生已经知道半个可以用个来表示，具备了画图表征半个及个的经验。

正确人数统计分析：

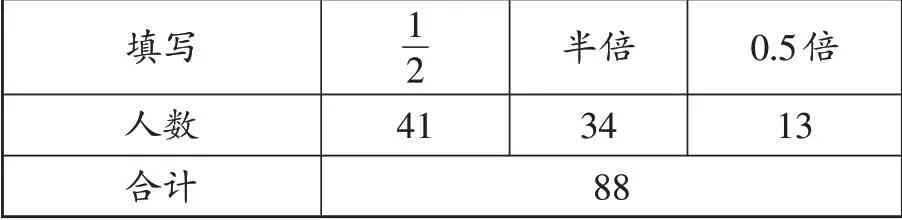
填写人数合计1 2 41半倍34 0.5倍13 88

（3）分数大小比较

正确人数统计分析：

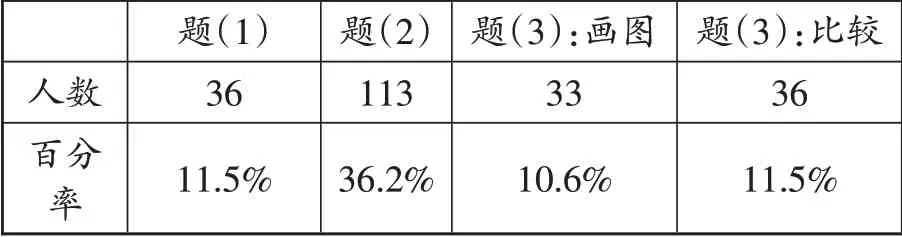
人数百分率题（1）36 11.5%题（2）113 36.2%题（3）：画图33 10.6%题（3）：比较36 11.5%

从表中可以看出，在有具体图形的帮助下，分数大小比较的正确率也是低的，其中同分母分数大小比较的正确率约是同分子分数大小比较的3倍。

2.知识衔接的分析

笔者对学生之前学习中积累的有助于分数学习的知识整理如下。

年级二下三上内容第二、四单元“表内除法”第五单元“倍的认识”知识联系平均分比率

平均分是理解分数含义的基础；比率大于1用“几倍”来表示，小于1 一般用分数表示。从“教材的排序”来看，比率与本单元初识分数的联系不是很密切，但对五下分数意义的学习有重要影响。从前测情况看，从平均分引出分数“量”和从“几倍”引出分数“率”的学习都是可行的。

三、立足儿童，整合设计

在审视教材与学情的基础上，笔者整合设计了“分数的初步认识”的单元架构并进行了尝试实践。

（一）“分数的初步认识”教学设计

1.尊重儿童认知思维

学生在三年级之前的数学学习过程中积累了大量的整数学习经验与思维，教学可从平均分物入手，借用除法含义，引出分物时得不到整数个可以用分数个表示，以此作为学生学习分数的思维起点。

2.立足单元文本价值

立足“分数的初步认识”中分数的含义、计算与应用三个知识内容与后继分数知识的关联度，将本单元学习课时进行重组、调整（见下表），让学生在初识分数时能多角度、多维度对分数含义进行深度感悟与理解。

整合前内容整合后内容分数的初步认识认识几分之一认识几分之几分数加法和减法练习课分数的简单计算分数的初步认识分数的简单计算分数的简单应用用分数解决问题练习课分数的简单应用认识几分之一（例1、例2）几分之一大小比较（例3）认识几分之几（例4、例5）同分母分数大小的比较（例6）分数加法、减法（例1、例2）1减几分之几（例3）多个同一事物组成的集合作为单位1（例1）解决问题求一个数的几分之几是多少（例2）整理与复习课时 1 1 1 1 1 1 1 1 1拓展课整理与复习修整课单元评价课时 1 1 1 1 1 1 1 1

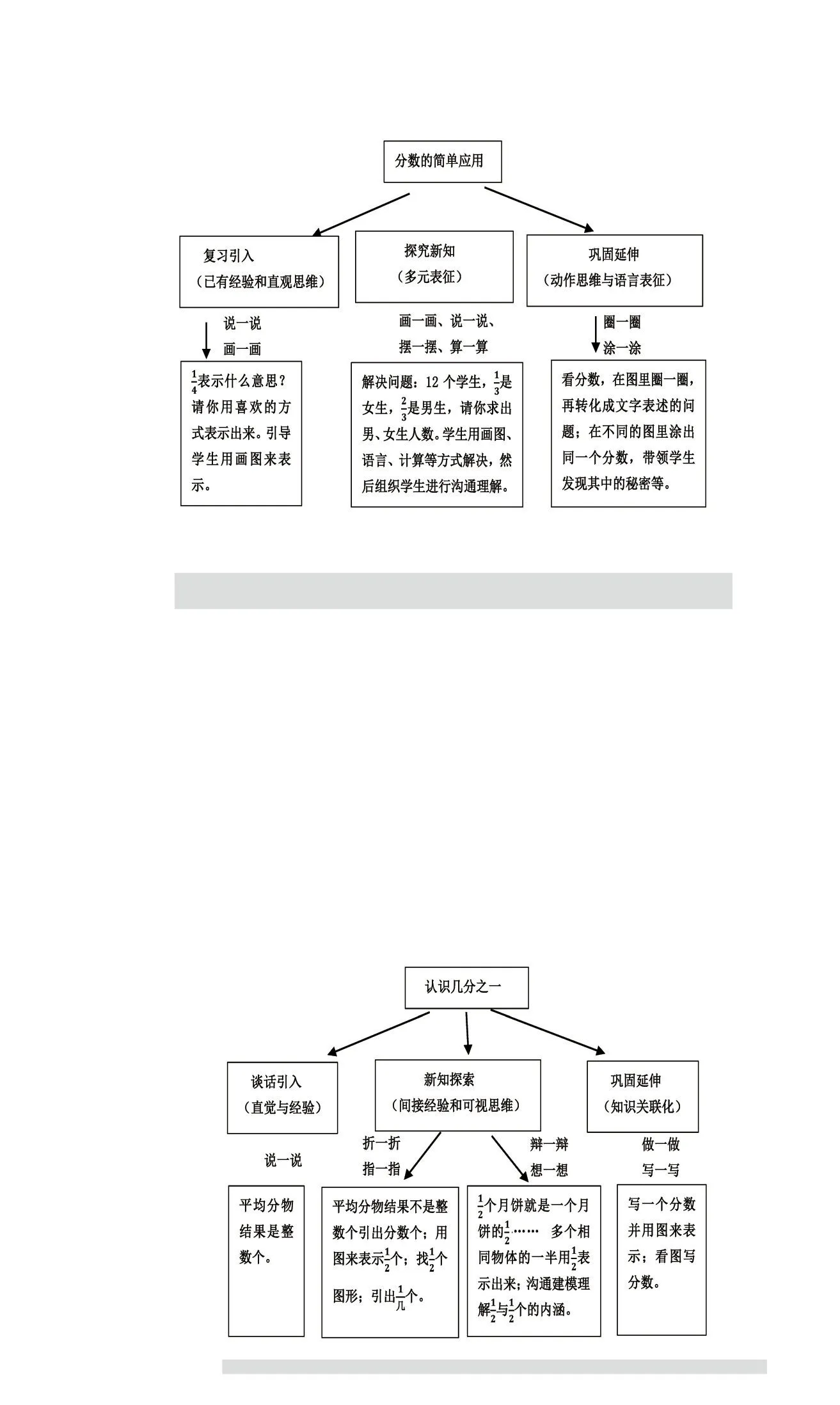
（二）“分数的初步认识”单元主要新授课教学思路架构

本单元教学内容是由整数拓展到分数，分数的概念更为抽象。它可以从部分到整体、分物、测量、比、算式和商等多个角度加以理解，是对数认识的一次飞跃。

1.“认识几分之一”教学思路——“量”“率”并行

平均分物，结果不能用整数个表示时，可以用分数个来表示；着眼点在分数表示具体量的理解，再从具体量引出分数作为“率”的含义。“认识几分之几”的教学思路与“认识几分之一”基本一致。

2.“分数的简单计算”教学思路——重“量”弱“率”

沿用认识分数含义建立平均分物的思路展开，搬用五下年级的分数加减法的具体量教材素材，大幅度减少本册“率”分数加减的素材，在分数“量”下理解分数的简单加减法，在操作中深刻感悟“相同的分数单位”才能相加减的策略。

3.“分数的简单应用”教学思路——轻“量”重“率”

本节课侧重于用分数“率”解决问题，特别是多个相同物体作为“1”，求一个数的几分之几是多少。引导学生在可视化的表征中理解掌握解决分数问题的多样化策略，进一步巩固分数作为“分率”的含义。

（三）教学实践——以“认识几分之一”为例

由于篇幅限制，在此具体展开“认识几分之一”的实践过程。教学中，应注重“量”“率”并行，引领学生在平均分物中充分感受分数的多样含义。

1.教学目标与重难点（略）

2.教学过程

（1）谈话导入：同学们记得平均分吗？

（2）互动游戏：用拍手来表示平均分到的个数。

a.把6个月饼平均分给2人，每人（ ）个。算式怎么列？4 个呢？2 个？1 个？此时追问为什么不拍手？

b.半个。列出算式。

（4）揭示课题：分数。

（设计意图：借助学生原有的认知基础与直觉经验，在平均分物的结果不能用整数个表示时，引出用分数个表示。学生对“半个”有充分的生活经验和操作经验，因此在直接追问中找出个，以此来沟通整数与分数之间的联系，让学生感悟到分数也可以用来计数，表示一个具体量。）

（2）展示作品，交流评价。

（4）思考：如果要平均分给4 人，每人得到几个？平均分给5人呢？6人呢？你认为还可以平均分给几个人，每人分得几个？

（2）观察并思考：为什么形状、大小、颜色各不相同，都表示这个物体的呢？（这些图形都是把1 个图形平均分成2份，表示其中的1份）

（3）思考：把4 个月饼平均分成2 份，这其中的1份，可以用表示吗？为什么？四人小组交流，再集体反馈。

（4）追问：把2 个月饼平均分成2 份，这其中的1份，可以用表示吗？6个呢？8个呢？10个呢？那只要怎么样我们都可以用表示呢？

（设计意图：用一句“还可以说”将分数从表示具体数量自然引入到表示“率”，在思考、观察、图形表征、思辨中认识的含义，在追问中深度理解“不管是1个还是几个，只要平均分成2份，其中的1份就用表示”。）

思考：这些分数有什么共同特点？几分之一，就是平均分成几份，表示其中的1份。

（3）选取学生中的1 份作业，1 份表示几分之一，2份呢？3份呢？

（4）巩固沟通：老师把1 米长的绳子平均分，……得到了几个分数？一起来说一说。选出其中2个分数比一比，说说这样比的理由，有什么发现？（设计意图：再次利用前面的素材个月饼，引出并由学生选择喜欢的分数用画图方式表征出来，在这个过程中侧重“率”的理解；接着利用学生画的素材引出后面几分之几的学习，同时根据巩固练习随机融入分数的大小比较。）

本课立足儿童视角，切准单元立意，借助“量率并行”这一策略认识几分之一，但每个环节的分数“量”“率”的侧重不一样。

四、后测分析，实践反思

（一）后测分析

通过对“分数的初步认识”单元整合设计实践后，在没有整理与复习的前提下，笔者对同一所学校三年级的86个学生做了后测，数据见下表。

维度具体内容后测 前测人数百分率看图写几分之几85 98.84%分数计算分数的简单计算83 96.51百分率分数的含义看图写几分之一85 98.84%13.46%分数大小比较看图分数大小比较80 93.02%11.80%% 0分数应用分数的简单应用70 81.40%1.20%

从表中可以看出，学生对分数含义（看图写分数）和分数大小比较（虽然是在结合看图写分数及分数简单计算或解决简单问题中进行学习）都掌握得较好；对之前没有任何接触的分数简单计算，正确率也比较高；分数的简单应用相对较难，但从后测卷来看，学生还是能用图形、算式等策略来解决问题的。

（二）实践反思

此次思考与实践，在给笔者带来收获的同时也促发了笔者的深入思考。教学立足学生学习整数平均分的经验，让他们深刻而充分地感悟到在平均分后不能用整数表示时，可用分数来表示；将分数表示一个具体的量（分数个）直接切入，实质上做了一个“分数”大单元的融合，将分数概念作为一个体系，以整体的角度来研究学习分数概念。在整合设计中，希望学生脑海中有一张逐渐清晰的分数概念图。学生对分数概念的理解不是一蹴而就的，教学任重道远。