搭建学习脚手架 培养抽象能力

□张丽芳 邢 颖

抽象能力是学生数学发展所必需的关键能力之一。《义务教育数学课程标准（2011年版）》（以下简称《课程标准》）将抽象思想、推理思想、模型思想确立为数学的“三个基本思想”。史宁中教授用三句话描述数学教学的最终目标：会用数学的眼光观察现实世界；会用数学的思维思考现实世界；会用数学的语言表达现实世界。数学的研究源于对现实世界的抽象，基于抽象结构，通过符号运算、形式推理、模型构建等数学方法，理解和表达现实世界中事物的本质、关系和规律。正是有了数学抽象，才形成了数学的第一个基本特征，就是数学的一般性。数学抽象在数学教学中无处不在。

小学生的学习主要以直观形象为主，教学中可以把抽象问题具体化、直观化，也可以从直观、具体事物中抽象出一般规律。搭建学习脚手架，让学生经历具体、抽象、再具体、再抽象的过程，相应的，学生的数学核心素养也伴随着这个过程渐渐形成。

一、多元表征，建立抽象概念

《课程标准》有关知识与技能的阐述中明确指出：让学生经历从日常生活中抽象出数的过程，发展学生的抽象思维。数概念贯穿于小学数学的整个教学过程，教师应在数概念建立过程中借助多元表征逐步培养学生的抽象能力。

为了使学生掌握数概念中诸多重要但又较抽象的内容，教学中加强学生的观察、操作活动至关重要。教师可为学生提供丰富的操作素材，如糖果、小棒、第纳斯木块、计数器等（见下图）。这些学习资源既是形成抽象数概念的桥梁，又为培养学生的数感提供了直观支撑。从实物抽象出数，再从抽象的数还原到实物，帮助学生完成由具体到抽象、再从抽象回到具体的认知过程。

认识数离不开直观的学具，呈现一堆“小棒”或“第纳斯木块”等，直接用眼睛看，看不出有多少，但若把这些学具“结构化”——10 根一捆，10 小捆一大捆，10 个一列，强调“十进制”，这时学生一眼就能看出物体的数量，由此感受“十进制”。再通过齐性、逻辑结构化的学具计数器让学生认识“珠子”相同，但珠子所在的位置不同，每个珠子所表示的意义也不同。从而形成计数单位的表象，逐步拓展对数位、计数单位的认知，并开始深入理解掌握十进位值制、数的内部结构，从而完成对数的逐步抽象的过程。

从实物到小棒、第纳斯方块再到计数器，从散乱的学具到齐性、直观、结构化的学具再到齐性、逻辑结构化的学具，将抽象的概念具体化、形象化，从具体到半抽象再到抽象逐步过渡，形成计数单位的表象，经历数概念的抽象过程，实现对学生抽象与概括的数学学科素养的培养。

学生抽象能力的培养不是一蹴而就的，是在学习知识的过程中借助多种表征方式逐步形成的。教学中教师要学会放手，给学生提供逐步抽象的空间，让学生在操作、思考、表征、表象过程中提高自己的抽象能力。

二、游戏引路，建构抽象模型

人教版五年级上册“用字母表示数”一课的主要教学目标是让学生理解“为什么要用字母表示数”“怎样用字母表示数”，教学有一定难度。因为由具体的数量过渡到可以用字母表示数，这是学生初次感知用字母表示数的抽象性和概括性，是由算术思维过渡到代数思维的关键点，对于学生来说是很抽象的，也是认识上的一次飞跃。

布鲁纳说：“学习的最好刺激是对学习材料的兴趣。”因此，本节课教师安排了游戏活动，以调动学生的学习兴趣，并在轻松愉悦的氛围中设置悬念，激发学生的探索欲望。

游戏一：通过创设情境，学生感受用符号、字母可以表示未知数，这里的字母表示的是固定的一个数。

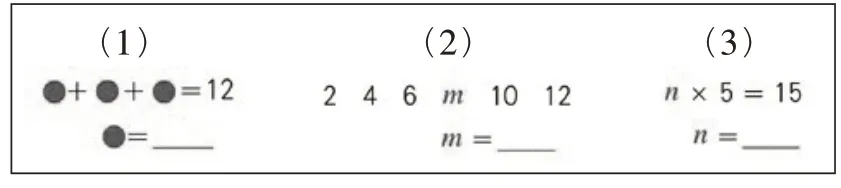
猜数游戏：同学们喜欢做游戏吗？我们先来做个猜数游戏，看谁猜得准。请你仔细观察屏幕上的信息，看看这些图形的后面藏的是几。想好后，举起手中相应的扑克牌。

课件逐一出示下图，学生举牌回答，逐一研讨：你是怎么猜到的？

游戏二：借助《数青蛙》这首儿歌，设置悬念，以激发学生的探索欲望。

师：你们喜欢儿歌吗？今天老师带来一首儿歌，相信你们只要听了第一句就能够继续说下去。（学生跃跃欲试）

师：（一边拍手一边说儿歌）1只青蛙，1张嘴，2只眼睛，4 条腿。怎么样，能不能继续往下说？我们一齐有节奏地说，还要说得流利，能做到吗？我们从头开始——

1只青蛙，1张嘴，2只眼睛，4条腿；

2只青蛙，2张嘴，4只眼睛，8条腿；

3只青蛙，3张嘴，6只眼睛，12条腿；

4只青蛙，4张嘴，8只眼睛，16条腿；

5只青蛙，5张嘴，10只眼睛，20条腿……

（加快节奏，使学生不能马上反应说出结果）

师：停……咱们刚才可说好的呀，要说得流利，怎么越说越乱了？

生：后面数越来越大了，不好说。

生：老师，数太大了，我们可以写一写吗？

师：就从6 开始写，要把这首儿歌写全啊！（引出新的问题）

放手给学生一点时间写，在写的过程中，有的学生写了几个就不写了，有的学生一直写。终于有人喊道：“受不了！太多了！”

当大多数学生发现写不完时，教师提问：你们又遇到困难了？写不完，能不能想想办法把这首儿歌写全？（学生很感兴趣，积极投入其中）

根据学生的回答，教师在屏幕上清晰呈现学生的作品。

生1：无数只青蛙无数张嘴，无数只眼睛，无数条腿。

生2：（N）只青蛙，（N）张嘴，（N）只眼睛，（N）条腿。

生3：（N）只青蛙，（N）张嘴，（B）只眼睛，（C）条腿。

生4：（A）只青蛙，（A）张嘴，（2×A）只眼睛，（4×A）条腿……

教师以学生感兴趣的猜数游戏和趣味儿歌作为素材，让学生在游戏中自己发现问题，自己解决问题，体会到用字母表示的是一类不确定的数的所有情况，抽象思维能力得到提高。

三、活动进阶，激活抽象思维

儿童的思维在活动中最活跃，设计进阶活动可以提升学生的抽象思维。聚焦人教版教材四年级下册“多边形内角和”这部分内容，起点为三角形内角和，随着图形边数的增加，内角和也在增加，在变化中不变的因素是图形的边数每增加1，内角和会增加180度。而教材练习十六中的第四题，要求依次探索多边形内角和。

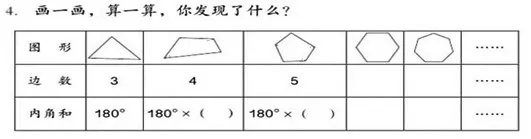
在教学这部分内容时，学生利用探索三角形内角和及四边形内角和积累的经验解决问题，并尝试用公式表达规律，极大地发展了抽象能力。

本单元内容可以做如下设计：以学生调研中提出的问题“100 边形内角和是多少度”作为大问题情境设计进阶学习活动。首先聚焦三角形内角和，在研究出三角形内角和是180度的同时，引导学生对研究方法进行对比、反思，积累活动经验。接着利用积累的学习经验依次探索多边形的内角和，感悟规律。最后利用规律解决问题，尝试用符号化表达规律。

活动一：学生通过量角求和、撕拼求和、分割求和等方法探究不规则四边形的内角和。

活动二：五边形、六边形的内角和是多少度呢？动手探究五边形、六边形内角和度数。

（1）用你喜欢的方法去验证一下你的猜想。

（2）收集资料并提出问题:①你觉得这个五边形或六边形内角和是多少度？②你用什么方法验证的？

活动三：100边形的内角和是多少度呢？

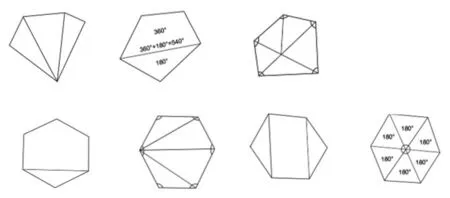
100 边形的内角和是多少度，学生感到非常惊讶，于是继续探索规律，其中必有规律可循。随着活动的一次次进阶，学生的思维异常活跃，活动就在学生的迫切需求中继续进阶。学生在探究多边形内角和时，利用分割图形法得出很多不同的情况（见下图）。

当教师问学生“你喜欢用哪一种方法”时，学生的意见并不统一。此时教师应不急于统一到全部分割成三角形，而是让学生继续用自己喜欢的方法先来研究多边形的内角和。于是学生有了下面的反馈：

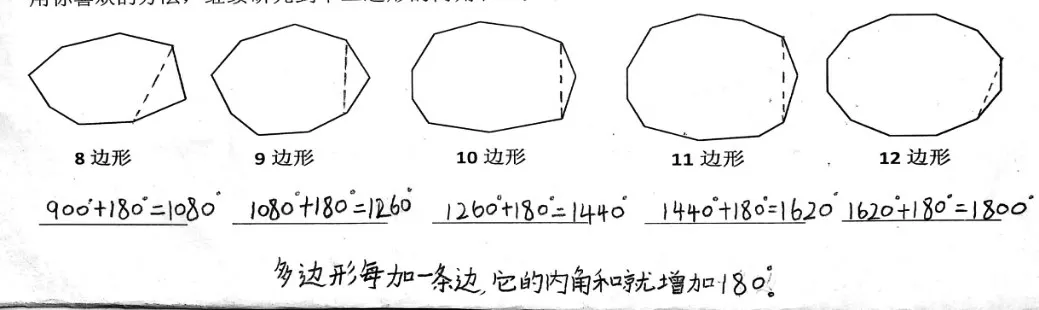
此时，教师首先呈现学生的作品，组织探讨：用这几种方法继续研究100 边形内角和怎么样？学生在观察比较中，发现这几种方法都可行，但第一种方法需要记住分出的每个图形的内角和是多少度，继续研究下去会越来越复杂；第二种方法要解决100 边形的内角和，就要先知道99 边形的，要知道99边形的就需要知道98边形的，也很复杂；第三种方法中的图形的边数都比三角形的个数多2，可以用这样的规律解决100 边形内角和的问题。学生在研讨的过程中有感而发：“n 边形的内角和就是n-2的差乘180度。”正是合理整合教材，才使符号化表达自然而然地出现在课堂上，学生的思维从具体形象走向抽象一般。

教学中在抽象概念的建立、抽象模型的建构、抽象思维的激活等方面，要注重采取各种形式，借助多元表征、借助游戏、借助操作、借助活动等都可以为学生搭建学习脚手架，凸显抽象过程，让学生亲身经历由具体到形象再到抽象的过程，进而培养学生的抽象能力。