明理悟法——运算能力提升的根基

□胡艳霞 曹 艳

在小学阶段，有关运算的内容贯穿数学教学始终，这是因为运算能力的培养关系着数学学习的基础，同时也是对学生逻辑思维以及非智力因素的一种培养。有关运算教学的重难点，每一位教师都会脱口而出，即掌握算法、理解算理。在实际教学中一线教师又是如何处理好算法和算理的关系的呢？笔者结合课堂教学谈谈如何帮助学生明理悟法，从而培养学生的运算能力。

一、情境中明理悟法

人教版教材中有关计算的教学都安排在情境中，这样的编排充分体现了数学与生活的密切联系，同时也能够借助情境帮助学生理解算理。如教学三年级下册“口算除法”时，教材创设了平均分手工纸的情境（如图1）。教师借此帮助学生理解60张纸即60 个一，同时也可以表示6 个一沓即6 个十。学生依据情境就可以进行直观理解：把6沓纸平均分给3个人，每个人得到2沓纸即20张。也可以用6 捆小棒代替6 沓纸，平均分给3 个人，每人2捆，就是2 个10。而6 沓纸和6 捆小棒虽然实物不同，但背后的道理是相通的。有了对情境的理解、自主的操作，学生再用数学语言表达算理就变得水到渠成了。

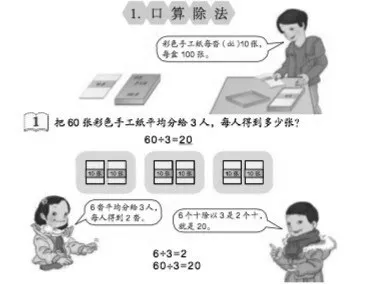
图1

二、经验中明理悟法

学生在学习相关知识时必会积累一定的经验，教师在进行计算教学时可充分利用学生的已有经验来促进学习的迁移。如在学习“小数加减法”之前，学生已经有了整数加减法的经验：①相同数位对齐。②满十向前一位进“一”。③从个位加起。对于小数加减法的学习来说，第①、第②条经验可以迁移；而第③条经验对于小数来说不再适用。那该从哪儿加起呢？小数加减法怎样做到“相同数位对齐”呢？教师创设了去新华书店买书的生活情境，以此唤醒学生已有的经验：小红买一本故事书花了8.67 元，买一本科技书花了5.9 元，带15 元够吗？学生体会到元和元相加，角和角相加，分和分相加，就是相同数位对齐。只要小数点对齐了，就能满足相同数位对齐，也就是“8 个1+5 个1；6 个0.1+9个0.1；7个0.01”合起来就是14.57元。

三、操作中明理悟法

在计算教学中教材依据学生的年龄特点呈现了各种学具，如实物原型、直观模型等，其中直观模型有小棒、计数器、第纳斯方块、点子图等。这些直观学具能够帮助学生更好地理解算理。然而在实际教学中，有些教师没有认识到直观学具的重要性，忽略了直观学具所发挥的作用。

例如人教版三年级下册“笔算除法”的教学，这是学生第一次学习除法竖式，教材呈现的是分小棒的情境，借助分小棒的实际操作，帮助学生理解除法竖式的算理。有位教师是这样展开教学的。

师：你们能通过画一画小棒图来说明42除以2的算理吗？

图2

一学生画了这样一张图（如图2）。

图3

师：这名同学是用画图的方法得到42除以2等于21 的。除了用画图可以得到结果，有的同学还用了列除法竖式计算的方法，我们一起来看看（教师课件呈现图3）。

师：你们都是这么写的吗？

生（答）：是。

师：你们写的除法竖式跟你们画的小棒图的意思一样吗？

生：一样。

执教教师认为三年级学生已经能够通过画小棒图理解算理，相对于画图，借助学具摆一摆不仅耽误课上的时间，而且比较麻烦。而笔者认为：由于学生已经学完了口算除法，他们利用口算就可以直接计算出结果。这时让学生画图呈现计算过程，学生更多地还是呈现了结果，没有把分的过程直观、形象地呈现出来。而借助小棒呈现分的过程，能帮助学生建立表象，进而让他们一下子就理解笔算除法的算理以及书写格式。在与教师沟通之后，我们又重新设计了本节课，先让学生独立笔算，教师呈现学生的各种算法。接着让学生借助小棒摆一摆，并对比辨析哪种笔算写法与自己分小棒的过程是一致的。这样一来，学生借助分小棒的过程真正理解了两位数除以一位数的算理，并最终形成运算能力。

四、模型中明理悟法

对数学运算法则、运算定律的理解和掌握是培养学生运算能力的基础，因此在教学中要让学生充分经历运算法则、运算定律的形成过程，对运算定律、运算法则有清晰的认识，并能够灵活运用其解决问题。如人教版四年级下册第三单元“运算定律”中的乘法分配律是教学的重点也是难点。直到六年级，学生依然在应用上会出现如图4 中这样的错误。归结这两种典型错误的原因，都是学生对乘法意义、运算含义理解不清造成的。这不仅说明机械化记忆不能对学习产生深远的影响，还反映出一部分学生对抽象的意义难以理解。以生活意义为基点、依托具体的数量关系建构的乘法分配律的模型并不能够让所有的学生都加以灵活应用。

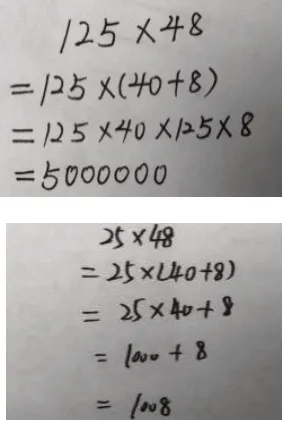
图4

在乘法分配律教学时，笔者采用了具有面积模型特征的情境，情境一为实物直观模型，情境二在情境一的基础上增加了图示的作用，使之变成矩阵模型（图形直观），情境三是在矩阵模型的基础上继续抽象变成面积模型（图形直观）。学生先依次解释三个直观图式情境，依据两种思路得到两个算式，再根据算式的意义与计算结果使学生建立起两个算式之间相等的联系，从而得到三个形式相同的等式，为第二环节发现规律做好充分的准备。教师通过多样化的数学活动，充分调动学生感官，丰富其感性认识，从而帮助学生更容易感知、理解乘法分配律，提高学生的几何直观能力，建立模型化思想。把运算从操作的层面提升到思维的层面，这是运算能力发展的重要内容。

点子图其实也是一种图形，它和长方形的作用相同。借助点子图，可以帮助学生区分结合律和分配律的本质特征。如教师设计了学生参加运动会入场式表演的情境：同学们要站成15×18的长方形队形，如果用一个黑点来代表一名学生，站好的队形就成了点子图这样的方阵。学生四人一小组合作，看哪个小组能用尽量多的方法来进行巧算，并把列式计算的想法在点子图上圈一圈。学生在汇报时一共出现了7种计算方法（见图5）。结合点子图与算式各部分之间的联系，通过交流、观察、归纳等数学活动，学生感悟到结合律是把数等分成相同的几组，所以连乘；而分配律是不等分，把数分成几个不同的块，所以乘加或者乘减。

图5

由于在教学中采用了形象化的点子图，直观地展示了两种运算定律的区别，枯燥的数学知识变得生动有趣，隐秘的特征变得清晰简明，学生不仅提高了计算的正确率，也喜欢上了数学，同时产生了积极的情感。

在课堂教学中，教师既要依据学生的年龄特点借助直观学具帮助学生理解算理，还要处理好算理与算法的关系，将算理与算法有机融合，为学生搭起理解的桥梁，这样学生才能由算理直观化过渡到算法抽象化，才能在“理”中形成“法”，在“法”中蕴含“理”，理法交融对于提高学生的计算能力具有重要的作用。将“讲理”与“明法”有机结合，学生在理解算理的基础上总结算法，能更深入地理解数学核心概念，更好地实现“培养学生根据法则和运算律正确地进行运算的能力”的目标。