X射线荧光光谱中低分离度重叠峰分解的方法研究

周世融，何剑锋1,*，任印权，汪雪元，叶志翔

1. 东华理工大学放射性地质与勘探技术国防重点学科实验室，江西 南昌 330013 2. 东华理工大学江西省放射性地学大数据技术工程实验室，江西 南昌 330013 3. 东华理工大学信息工程学院，江西 南昌 330013

引 言

X射线荧光光谱分析是一种重要的放射性检测方法，广泛的应用在地质、环境和考古等领域。 重叠峰分解是X射线荧光光谱分析中至关重要的一步。 近年来，国内外研究人员提出了多种重叠峰分解方法，主要包括： 导数法[1]、小波变换法[2-3]以及Boosted-Gold反卷积法[4-5]等。 当重叠峰分离度较低时，上述方法很难实现分峰或分峰结果误差大。 林兆培等[6]将二阶微分与小波变换结合用于分解色谱重叠峰，其仿真实验仅对分离度大于0.4的重叠峰实现了分离，且没有对其分离结果的误差进行分析。 罗海军等[7]提出峰锐化法可以减小峰宽，从而提高信号的分辨率。 朱晨超等[8]将双树复小波变换与实数小波变换进行对比，结果发现双树复小波变换能够分解分离度更低的重叠信号且分峰结果更准确。 当试样中存在X射线能量十分接近的元素时，X射线荧光光谱的谱峰会严重重叠甚至完全重叠。 针对这一问题，提出了一种峰锐化法结合双树复小波变换分解低分离度重叠峰的新方法，来解决X射线荧光光谱中谱峰严重重叠的问题。

1 原 理

1.1 峰锐化法理论

传统峰锐化法是通过将原始信号与其负的二阶微分处理后的信号的加权相加[7]，表达形式如式(1)

F=f-kf(2)

(1)

式(1)中，F为经过锐化后的重叠信号，f为原始重叠信号，f(2)为二次微分处理后的信号，k为加权因子。 经二阶微分运算后的信号极值点位置与原始信号极值点位置一致，用式(1)对重叠信号进行变换，可以突出原始信号的峰位特征，从而实现重叠峰分解。 其中，k的值越大，峰的锐化程度越大。

1.2 双树复小波变换理论

近年来，利用小波变换对重叠峰进行分解受到了广泛使用。 传统离散小波变换系数存在正负震荡，且在下采样过程中，容易产生混叠现象[9]。 Kinsbury等提出双树复小波变换(DT-CWT)算法，该算法具有近似平移不变性以及完美重构性的特点[10]。

双树复小波变换算法采用两棵独立的实数小波变换树对信号进行分解与重构，表达式如式(2)

Ψ(t)=Ψh(t)+iΨg(t)

(2)

其中，Ψh(t)为实部实数小波，Ψg(t)为虚部实数小波。 在双树复小波分解与重构过程中，两棵实数小波变换树的采样点具有互补性，使得两树的分解系数可以充分利用。 双树复小波变换的分解与重构过程(三层为例)如图1所示。 其中，h0a，h0b，g0a和g0b为低通滤波器，h1a，h1b，g1a和g1b为高通滤波器。

双树复小波变换分解重叠峰的步骤如下：

(1)选择适当的分解层数和滤波器组，对原始重叠信号进行双树复小波分解，分解后可以得到各个尺度的细节系数{d1；d2; …；di}和最终分解尺度的近似系数ci。

(2)选择某一分解尺度L下，能表征原始信号的细节系数dj，并用大于1的倍数n乘以该细节系数，对其放大。

(3)用放大后的细节系数代替原细节系数，与其他复小波系数进行重构，通过调节放大倍数n，实现对重叠峰不同程度的分解。

1.3 峰锐化法结合双树复小波变换分解低分离度重叠峰

分离度Rs是色谱分析中用来判断两相邻色谱峰分离情况的一个指标。 其定义为两峰保留时间的差值与两个单峰峰宽平均值的商[11]。

(3)

其中，t2和t1分别为两相邻谱峰的保留时间，即t2-t1为相邻峰的峰位差；w1和w2分别为两个峰的峰宽。 即Rs越小，谱峰重叠程度越高。

多个高斯函数叠加模拟重叠峰可用式(4)形式表示

(4)

其中，i=1, 2，…，m表示重叠的高斯峰个数；ai表示各个高斯函数的峰值；bi表示各个高斯峰的峰位；ci表示各个高斯峰的标准差。

即两组分高斯重叠信号的分离度表达式如式(5)

(5)

模拟两组重叠峰如式(6)和式(7)

(6)

(7)

分离度Rs分别为0.56和0.38。 实验采用Kingsbury等[12]设计的Q-shift结构的双树复小波变换进行信号处理。 在双树复小波变换分解重叠峰的过程中，随着细节系数的放大，信号的高频部分变大，则重叠峰的分离程度会变大。 但当选取的放大倍数太大时，峰形会严重失真，造成重叠峰分解的结果不准确。 通过大量仿真结果发现： 双树复小波变换的细节系数放大倍数控制在1～10范围内，分解层数在2～6之间，第一层采用near_sym_b滤波器，第一层以上采用qshift_d滤波器时，重叠峰的分解结果更准确。 分别使用峰锐化法和双树复小波变换对两组重叠信号进行处理，结果如图2所示。

图2 模拟重叠峰分解结果对比

得出结论： 当Rs=0.56时，两种方法都实现了重叠峰分解； 当Rs=0.38时，后一组分高斯峰的特征已经几乎无法识别，两种方法都没有实现对该低分离度重叠峰的分解。 而用峰锐化法处理后的信号出现峰形变尖，谱宽变窄，即分离度Rs增大的现象。 对锐化后的信号进行双树复小波变换。 图3中，d1，d2，…，d5为原始信号复小波分解的五层细节系数，dd1，dd2，…，dd5为锐化后信号复小波分解的五层细节系数。 可以发现，dd3和dd4能较好表征两组分重叠峰的特征，且分离度较大。 选择第三层细节系数进行放大，式(7)的重叠峰分解结果如图4所示，结果表明： 峰锐化法结合双树复小波变换能够实现对低分离度重叠峰的分解。

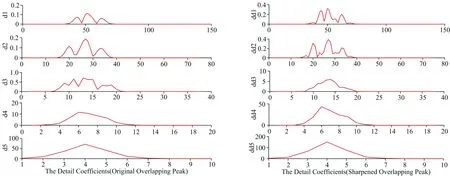
图3 双树复小波分解的细节系数

2 仿真实验

对照X射线能量表： K元素的Kα为3.313 keV,Kβ为3.589 keV, 能量相差276 eV； Fe元素的Kβ为7.057 keV和Co元素的Kα为6.930 keV，他们之间的能量差为127 eV等。 当光谱仪测量试样中包含上述元素时，光谱谱峰会严重重叠。 已知一组K系谱线不重叠的光谱，识别其能量峰道址作为标准能量峰道址，进行能量线性刻度:E=0.030 7 keV·ch-1(0～5 ch的相对计数值为噪声，无实际意义)。 即K元素Kα能量峰道址与其Kβ能量峰道址分别为113(+5)与122(+5)； Fe元素Kβ能量峰道址与Co元素Kα能量峰道址分别为235(+5)与231(+5)。 用式(4)模拟 X射线荧光光谱中存在的两组低分离度重叠峰，模拟表达式如式(8)和式(9)。 采用峰锐化法结合双树复小波变换对两组模拟重叠光谱进行分解，如图5和图6为重叠峰分解和特征峰拟合的结果。

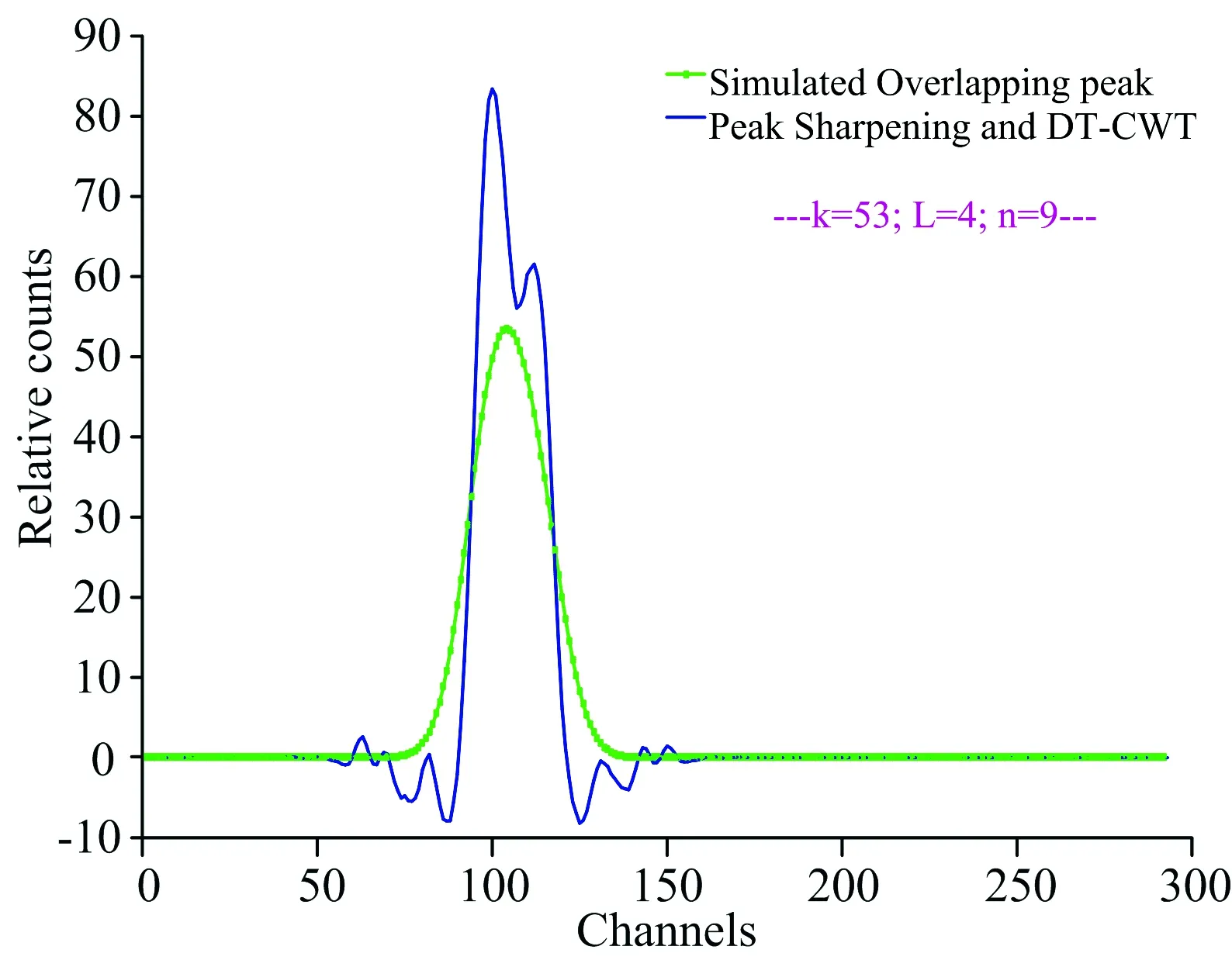
图4 低分离度(Rs=0.38)重叠峰分解结果

(8)

(9)

如图5和图6所示，模拟X射线荧光光谱的重叠峰都实现了分解。 图6中，重叠峰的分离度Rs已经低至0.34。 识别分解后信号的峰位，并求出拟合后的峰面积。 结果如表1所示，峰位和峰面积的相对误差分别在1%和6%以内。 结果表明，峰锐化法结合双树复小波变换能较好的分解X射线荧光光谱中的低分离度重叠峰，具有可行性。

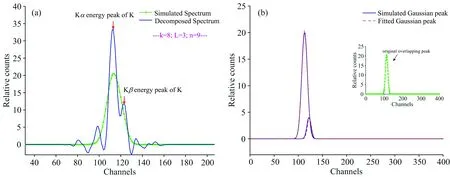
图5 模拟重叠光谱分解(a)结果和特征峰拟合(b)结果

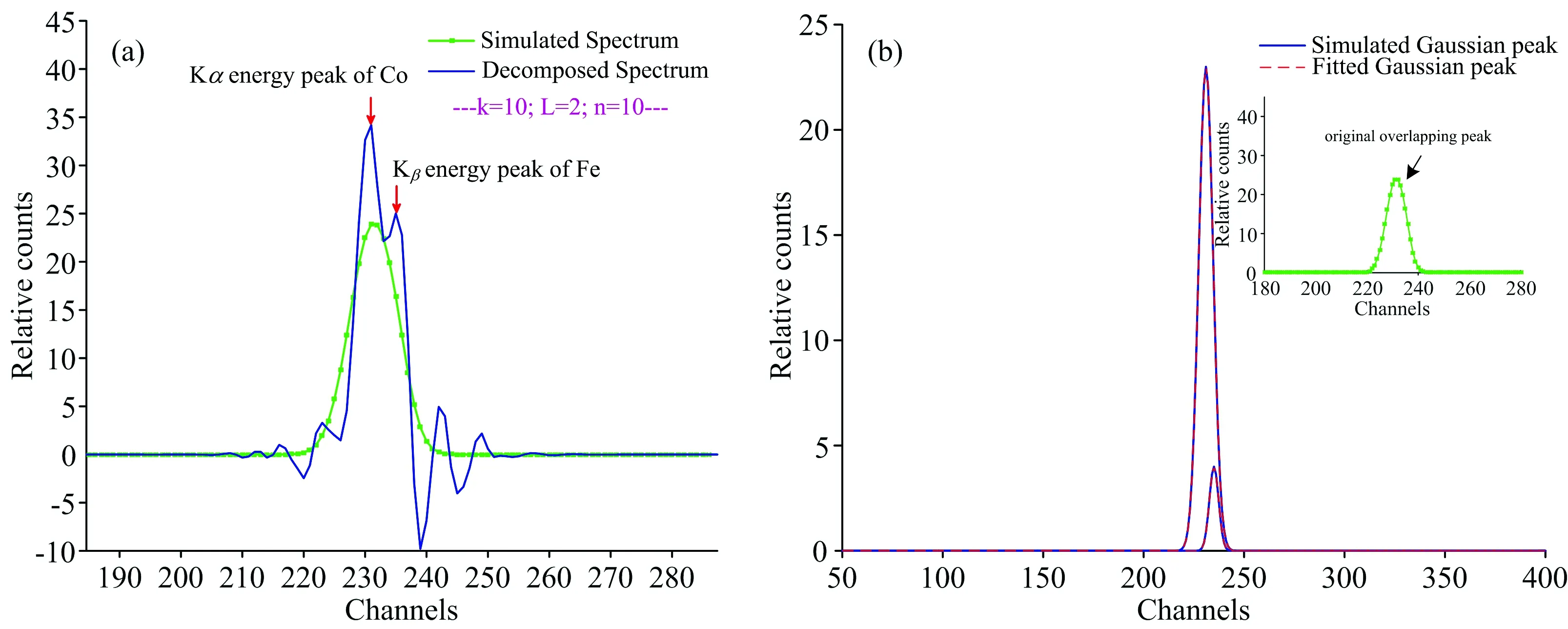
图6 模拟重叠光谱分解(a)结果和特征峰拟合(b)结果

3 实测X射线荧光光谱重叠峰分解结果

实验室采用Si-PIN探测器测量样品，受测量环境的影响，实测谱线的分辨率达到了340 eV左右。 图7(a)为实测的Ca元素X射线荧光光谱。 可以看出： 该谱线存在严重重叠且无法识别出Kβ能量峰的位置。 先对光谱进行平滑以及扣除本底处理，再用峰锐化法结合双树复小波变换分解重叠光谱，重叠峰分解结果如图7(b)所示。

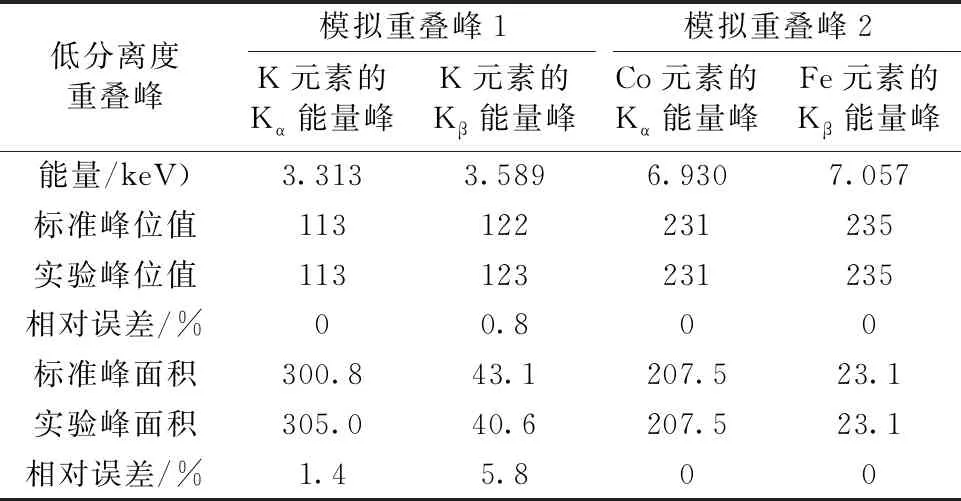
表1 峰位、峰面积误差分析

已知实测光谱与上述进行能量刻度的光谱是在同一仪器和相同测试环境下测得的，即该光谱的标准峰位仍然可用上述能量刻度公式求出。 识别分解后光谱的峰位，结果如表2所示： Ca元素的Kα能量峰与其Kβ能量峰分解后的峰位相对误差分别为0.8%与0.7%。 结果证明了峰锐化法结合双树复小波变换能够分解X射线荧光光谱中的低分离度重叠峰且分解结果较精确，具有实用性。

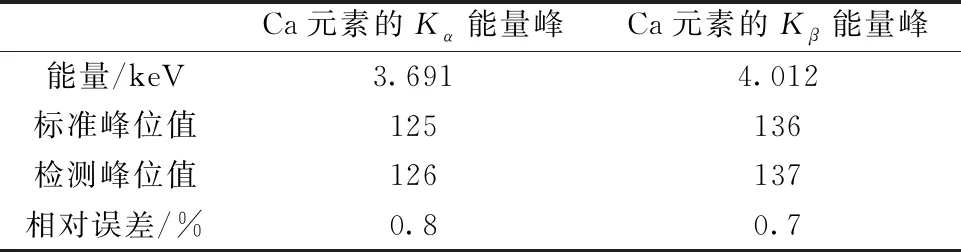
表2 峰位值结果分析

4 结 论

研究了峰锐化法以及双树复小波变换分解重叠峰的原理，提出了一种峰锐化法结合双树复小波变换分解低分离度重叠峰的新方法。 通过仿真实验结果表明，该方法能够实现对低分离度重叠峰的分解。 同时，用该方法处理了模拟重叠光谱和实测重叠光谱，最终都实现了重叠峰分解且分峰结果误差较小。 结果表明： 新方法能有效分解低分离度重叠峰，且在解决X射线荧光光谱谱峰严重重叠的问题上，具有实用性。