地表水亚硝酸盐氮浓度紫外可见光谱检测方法的基础研究
2020-05-07李庆波何林倩崔厚欣郝龙腾孙冬生
李庆波,何林倩,崔厚欣,郝龙腾,孙冬生
1. 北京航空航天大学仪器科学与光电工程学院,精密光机电一体化技术教育部重点实验室,北京 100191 2. 河北先河环保科技股份有限公司,河北 石家庄 050035
引 言
地表水是人们生活和生产用水的主要来源,随着我国经济发展和城镇化的加剧,地表水的污染严重威胁社会用水安全,因此加强地表水的监测迫在眉睫[1]。 “十三五”期间,国家出台了“河长制”、“水十条”、以及《水污染防治法》等一系列政策,推进水污染防治工作的发展。
亚硝酸盐氮是氮循环的中间产物,对人和牲畜具有较大的毒性。 当其进入血液时,会将正常的携带氧气的血红蛋白氧化为不具备携带氧气能力的高铁血红蛋白,进而导致组织缺氧。 在pH<6.5时,它会与仲氨反应形成具有强致癌性的亚硝胺。
紫外-可见光谱法具有检测速度快、维护成本低、无二次污染等优点,近年来被广泛用于水质监测等各个领域。 测定亚硝酸盐的方法主要有: 离子色谱法、气相分子吸收光谱法、流动分析法、紫外可见分光光度法等[2-3]。 离子色谱法、气相分子吸收光谱法和流动分析法适用于实验室检测,不适合于地表水的现场连续检测。 国内关于紫外可见光谱法检测亚硝酸盐氮的文献中,多需要在酸性介质中通过添加化学试剂生成显色染料再利用紫外分光光度计预测浓度[4]。 其中国标水质亚硝酸盐氮的测定分光光度法[5]采用的试剂盐酸萘乙二胺具有致癌性,不受操作者欢迎。 这种方法需要化学前处理的操作,不仅检测步骤繁琐,耗时耗力,还会对环境进一步造成污染。 此外,这种方法也无法实现地表水水质的无人值守自动实时检测。 无化学预处理的基于紫外可见吸收光谱法的亚硝酸盐氮浓度预测鲜有文献提及。
采用偏最小二乘回归法(partial least squares regression, PLSR),选择190~500 nm谱段建立模型,对不同浓度的亚硝酸盐氮溶液进行分析。 该方法无需添加任何化学试剂,操作简便,可为日后地表水无人值守自动实时检测提供参考。
1 实验部分
1.1 仪器设备与溶液配制
采用美国海洋光学公司的USB2000+型号的微型光谱仪,波长范围为190~700 nm,波长分辨率为1 nm。 将实验室配制的1 000 mg·L-1的亚硝酸钠母液(以N计)稀释,配成0.2,0.4,0.6,0.8,1.0,2.0,3.0,4.0,5.0,6.0,7.0,8.0,9.0和10.0 mg·L-1系列标液,分别在第一天,第二天,第五天用1cm比色皿用紫外可见光谱计多次进行光谱扫描,扫描范围190~700 nm,记为D1组,D2组,D3组,一共42个样本。
1.2 数学模型
采用偏最小二乘回归法(PLSR)建立模型[6],其原理是对浓度矩阵Y和对应的光谱矩阵X同时进行主成分分解
X=TP+E
(1)
Y=UQ+F
(2)
式(1)和式(2)中T和U是X和Y矩阵的得分矩阵,P和Q分别表示X和Y矩阵的载荷矩阵,E和F分别是误差矩阵。
经过主成分分解后对得到的各列正交的特征矩阵T和U矩阵进行回归:
U=TB依据式(3)计算权重矩阵B
B=(TTT)-1TTU
(3)
在实际的算法实现过程中,PLSR方法将矩阵的分解和回归运算合并,即同时分解X和Y矩阵,并将Y中包含的信息传递至X的分解中,使得X主成分直接与Y关联。 将构建完成的模型用于未知样本预测时,首先获取该样本(记为X′)的得分矩阵T,而后基于式(3)计算预测结果,见式(4)
Y=TBQ
(4)
2 结果与讨论
2.1 光谱整体特征与评价指标
水样的紫外可见吸收特征光谱在210 nm附近具有很强的吸收,吸收带主要分布在190~500 nm,而在500 nm之后的吸光度接近于零。 为了更清晰的分析水样的紫外可见光谱,除去接近于零的波段,即保留190~500 nm的紫外可见波段进行建模(见图1)。
基于PLSR模型建立样本指标与光谱吸收率的关系,采用均方根误差(root-mean-square error, RMSE)来衡量建模的精度,计算公式如式(5)[7]
(5)

(6)
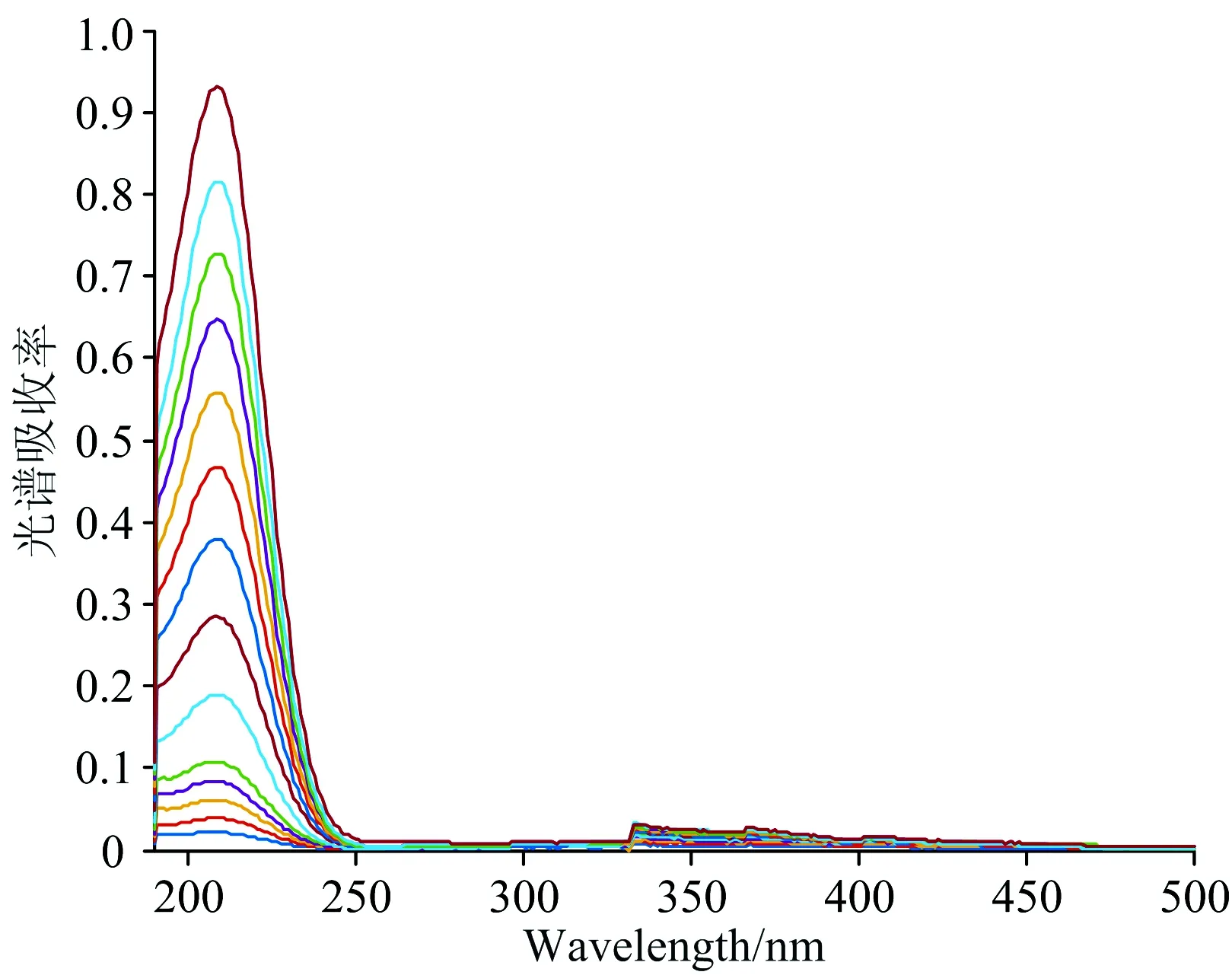
图1 亚硝酸盐氮溶液样本的紫外可见吸收光谱
2.2 PLSR模型的可行性分析
2.2.1 单日的样本交互验证预测分析
由于实验样本个数较少,采用留一交互验证法对数据进行建模预测。 即对单日的14个样本,每次用13个样本进行建模,预测剩下的一个样本。 重复试验14次,直到所有的样本都被预测一次为止。 分别取前两天的各14个样本,用14次试验的MAPE作为评价指标。
D1组的实验样本通过留一法交互验证得到最佳的主成分个数为6,每一个样本的相对误差范围在-1.67%~5.00%之间,RMSE结果为0.055 mg·L-1,平均绝对相对误差(MAPE)为1.19%; 除了在0.2 mg·L-1处相对误差为5.00%,其余浓度预测结果均低于5%。 D2组样本集通过留一法交互验证得到最佳的主成分个数为4,每一个样本的相对误差范围在-5.00%~6.00%之间,RMSE结果为0.075 mg·L-1,平均绝对相对误差为1.85%; 除了在1.0 mg·L-1处相对误差为6.00%高于5%,其余浓度预测结果均低于5%。 此结果说明PLSR模型具有优良的预测精度。
2.2.2 不同日之间互相预测分析
由于实验设备每次开机会产生不同的随机误差,可能会对建模预测产生影响。 为了验证PLSR模型在不同条件下的适应性,取前两天的实验数据进行互相预测分析。 即用一天的14个样本建模,预测另一天的14个样本的浓度。
实验结果表明,除了低浓度样本的预测结果的相对误差在20%左右,模型在其他浓度范围内都有很高的预测精度,两天互相预测的相对误差平均值分别为3.36%和4.51%,低于5%,RMSE结果分别为0.108和0.083 mg·L-1,证明PLSR模型的适应性强,鲁棒性好。
2.3 PLSR模型的实际水质预测
2.2.1节和2.2.2节的实验表明PLSR模型的鲁棒性好,预测精度高。 现将D3组的14个样本作为测试集,测试所建立的PLSR模型的预测精度。 将D1组和D2组的28个样本用于建模,利用留一法交互验证调整模型参数,再用最佳模型预测D3组的14个样本。
为模型设置不同个数的主成分,通过留一法交互验证,计算选用不同的主成分个数的情况下得到的训练集建模精度。 如图2所示,随着主成分个数N的增加,MAPE呈下降趋势,在主成分个数N=7时,训练集的平均相对误差最小,为2.02%,最优参数下的PLSR模型在3D上预测结果如图3所示,测试集样本的真实浓度和预测集浓度具有很强的相关性,见图3(a)测试集平均相对误差为2.19%,RMSE为0.044 mg·L-1, 见图3(b)。 测试集的平均绝对相对误差为2.19%, RMSE为0.044 mg·L-1。
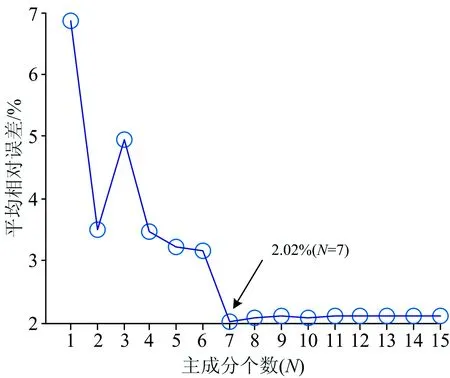
图2 PLSR模型选用的主成分个数与建模精度的关系
Fig.2RelationshipbetweenmodelingaccuracyandthenumberofprincipalcomponentsselectedinPLSRmodel
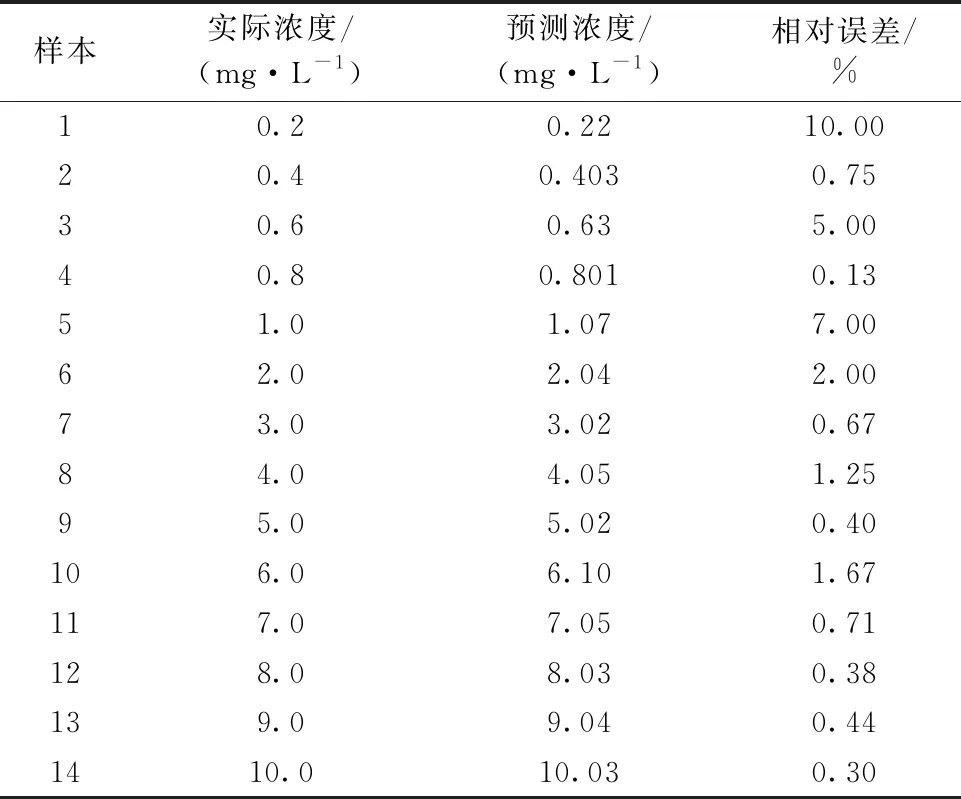
表1 PLSR模型对D3组14个样本的预测结果

图3 建立的PLSR模型在测试集D3上的预测结果分析
Fig.3TheanalysisofthepredictionresultonD3datasetachievedbythecalibratedPLSRmodel
(a): The linear relationship of test set date;
(b): The relative error of test set date
由表1可知,除了测试集在0.2和1.0 mg·L-1的绝对相对误差相对较差,其他浓度范围都有低于5%的不错的预测误差,平均绝对相对误差为2.19%。
3 结 论
将传统的线性建模方法偏最小二乘回归法应用于亚硝酸盐氮溶液的浓度检测,通过对数据进行偏最小二乘回归,从数百维复杂的光谱数据提取出主要信息,并压缩维度,降低整个模型的复杂度并用留一交互验证法选出最优模型。 通过同一天交互验证,不同天互相预测验证了PLSR非常适合亚硝酸盐氮检测,鲁棒性强,预测精度高。 最终确定的模型在0.2~10.0 mg·L-1浓度范围的平均绝对相对误差为2.19%,除了在低浓度0.2和1.0 mg·L-1的平均相对误差为10%和7%,其余浓度范围都具有低于5%的较好的预测精度,PLSR可以用于亚硝酸盐氮的快速无损检测。
