深度神经网络在红外光谱定量分析VOCs中的应用

张 强，魏儒义，严强强，赵玉迪，张学敏，于 涛

1. 中国科学院西安光学精密机械研究所，中国科学院光谱成像技术重点实验室，陕西 西安 710119 2. 中国科学院大学光学学院，北京 100049

引 言

大气污染防治是当前环保工作的重点之一，而大气中浓度过高的挥发性有机化合物(volatile organic compounds，VOCs)严重影响了空气质量、气候变化以及人类的健康[1]。 VOCs主要包括烃类、苯系物、氯化物、有机酮、胺、醇、醚、酯、酸和石油烃化物等，它们可通过呼吸道进入人体，造成纤维化肺泡炎、肺癌等严重危害，此外作为臭氧(O3)和细颗粒物(PM2.5)的重要前体物，严重危害环境质量[2-3]。 全面防治大气污染的前提是准确监测大气中VOCs的浓度，遥感-傅里叶变换红外光谱(remote sensing-Fourier transform infrared spectroscopy, RS-FTIR)技术由于其多通道、高通量、低杂散光且不需要进行样品制备和处理等优点，可实现大范围下的多组分实时监测, 测量速度快，检测精度高，广泛应用于国内外的大气监测领域[4-5]。

利用FTIR红外光谱对多组分VOCs进行浓度反演需要进行多元分析，传统的多元分析方法包括最小二乘法(CLS)、偏最小二乘法(PLS)、卡尔曼滤波法(KFM)、主成分回归法(PCR)、非线性最小二乘拟合(NLSF)等。 有报道采用非线性模型多项式偏最小二乘法(polynomial partial least square, PPLS)，对苯和氯仿的浓度预测均方根误差分别达到了0.043和0.087。 2011年，冯明春[6]等采用非线性最小二乘法拟合乙炔(C2H2)和乙烷(C2H6)的混合气体，拟合均方根误差分别为0.088和0.104。 在实际测量中，由于待测样品中各个组分之间的相互影响以及仪器自身的背景噪声会使近红外吸收光谱与样品浓度之间存在一定程度的非线性关系，尤其是当样品浓度范围较大时非线性更加严重，而对这种非线性关系的拟合能力则是准确预测的关键。 相比于传统的化学计量学方法，以反向传播人工神经网络(back-propagation artificial neural network，BP-ANN)为代表的深度学习回归方法可以逼近一些非线性关系的函数，越来越多的科学研究人员将其应用在红外光谱的定量分析中。 有研究用18-7-8的BP-ANN模型，对8种VOCs混合物进行了浓度反演，各组分标准预测误差(%SEP)的平均值为8.69%，平均预测误差(MPE)的平均值为-1.985，平均相对误差(MRE)的平均值为0.084，结果满足多组分微量气态污染物的定量要求。 2006年，刘丙萍等利用人工神经网络(ANN)对严重混叠的傅里叶变换红外光谱图进行了定量和定性的解析，苯乙烯和1,3-丁二烯这两种气体的标准预测误差(%SEP)分别为2.14和2.99。 人工神经网络能够拟合一定的非线性关系，因此在VOCs红外光谱定量分析中有着较好的应用，但ANN需要利用先验知识人工提取特征作为输入，且浅层的网络结构拟合复杂的非线性关系时，具有一定的局限性。

随着计算机科学的进步，特别是GPU的发展大大提高了网络计算的速度，深度神经网络(deep neural network, DNN)越来越多的被用于非线性系统的回归预测中, 在许多领域都表现出了最先进的性能[7]。 DNN可以自动提取特征，甚至将低级表示转化为更抽象的级别，对于无关和具有复杂参数的特殊微小变化可以达到更高的精度[8]。

本文利用DNN对FTIR谱图存在严重混叠干扰的苯(Benzene)、甲苯(Toluene)、1,3-丁二烯(1,3-butadiene)、乙苯(Ethyl benzene)、苯乙烯(Styrene)、邻二甲苯(O-xylene)、间二甲苯(M-xylene)、对二甲苯(P-xylene)等8种VOCs气体组成的混合污染物浓度进行测定，用反演结果的均方根误差(RMES)来评价其预测能力。 结果表明，使用DNN对多组分大气污染物浓度进行定量分析，能够得到精确地结果； 当训练样本充足时，相比于ANN，DNN对非线性关系的学习能力更强，反演精度更高，模型更为稳定。

1 理论部分

1.1 Beer-Lambert定律

利用气体的吸光度谱对VOCs进行浓度反演的理论依据是Lambert-Beer定律。 在路径上的大气各向同性且处于热平衡状态下，气体的吸光度Aν与气体浓度c和光程L的乘积成正比，即[9]

(1)

依据Beer-Lambert定律，当不考虑散射以及仪器本身的影响时，光程L为常数，吸光度Aν与气体浓度c成正比，因此可以直接利用吸光度谱进行计算，这种方法的理论基础是假设测量光路上的大气气溶胶散射对光程的影响以及大气光谱仪探测器自身的响应曲线在测量波段内与分子的振转光谱结构相比是一个随着频率变化缓慢发生变化的量[10]。 但在实际应用中，由于待测样品中各个组分之间的相互影响以及仪器自身的背景噪声会使近红外吸收光谱与样品浓度之间存在一定程度的非线性关系，尤其是当样品浓度范围较大时非线性更加严重，而对这种非线性关系的拟合能力则是准确预测的关键。 因此，需要根据待测样品的非线性特点建立相应的非线性校正模型[11]。

1.2 深度神经网络

深度神经网络(DNN)指具有一定深度的神经网络，根据不同的实际应用需求，具有不同的网络结构。 以多层BP神经网络为代表的深度前馈神经网络广泛应用于非线性系统建模，来拟合难以用数学方式描述的非线性系统，其特点在于信号的前向传输和误差的反向传播。 在信号前向传输中，通过隐藏层逐层计算输入信号，得到输出信号，如果输出信号与预期值误差太大，便转入反向传播并通过调整网络权值和阈值，让网络的预测输出逐渐靠近预期值。 图1是深度神经网络拓扑结构图，其中x1,x2, …，xm是网络的输入值，y1, …，yn是网络的输出值。

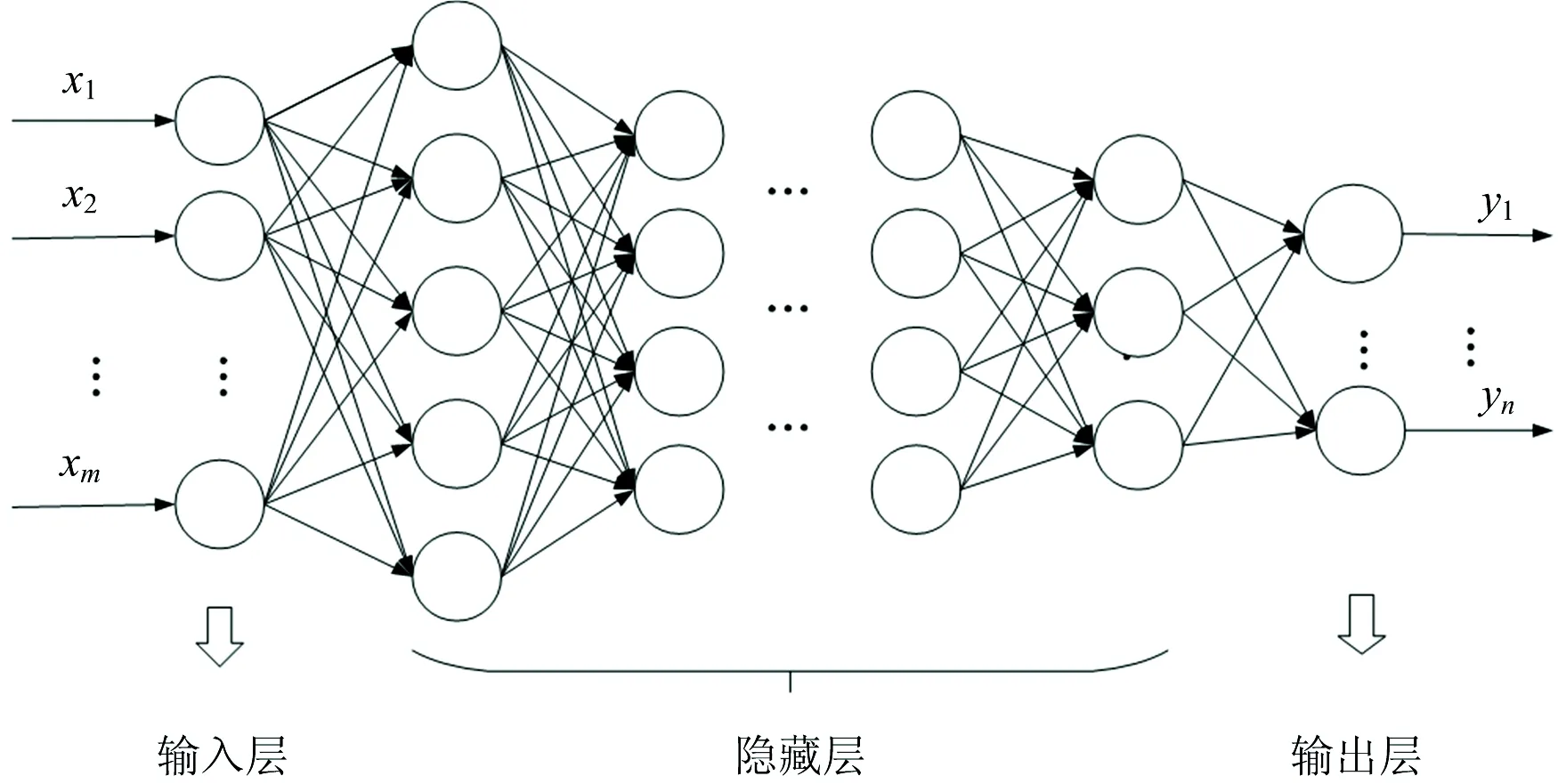
图1 深度神经网络拓扑结构图

深度神经网络训练的步骤包括：

(1) 网络初始化。 根据输入矩阵X和输出矩阵Y，结合经验公式，确定神经网络的总层数为L以及各层的节点数pl(l=1, 2, …,L)； 随机初始化各个隐藏层和输出层之间的权值矩阵Wl和偏移向量bl(l=2, 3, …,L), 确定学习速率η、迭代阈值ε和神经元激励函数。

(2) 计算出每个隐藏层和输出层的输出Hl。

Hl=f(zl)=f(WlHl-1+bl)l=2, 3, …,L

(2)

式(2)中，f为神经元激励函数，式(3)是本文选用的隐藏层神经元激励函数Sigmoid函数的表达式，式(4)是输出层神经元激励函数ReLU函数的表达式。

(3)

f(x)=max(0,x)

(4)

(3) 根据式(6)，利用损失函数J的计算公式计算出输出层的梯度δL。 选用的均方差函数作为损失函数，式(5)是其表达式。

(5)

δL=J(W,b,X,Y)⊗f′(zL)

(6)

(4) 计算出每各隐藏层的梯度δl[式(7)]

δl=(Wl+1)Tδl+1⊗f′(zl)l=L-1,L-2, …，2

(7)

(5) 调整各隐藏层和输出层的权值矩阵Wl和偏移向量bl[式(8)]

Wl=Wl-ηδl(Hl-1)T

bl=bl-ηδll=2, 3, …,L

(8)

(6) 根据阈值ε判断算法迭代是否完成，如果没有完成，回到步骤(2)。

利用深度神经网络模型进行回归预测，首先需要用训练样本来训练神经网络，让网络可以准确地描述输入与输出之间的未知关系，然后利用训练好的神经网络预测待测样本的输出。

1.3 模型评价

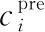
(9)

2 结果与讨论

2.1 数据来源

选取EPA数据库中苯、甲苯、1,3-丁二烯、乙苯、苯乙烯、邻二甲苯、间二甲苯、对二甲苯等八种挥发性有机化合物在8～12 μm(对应波数为833.3～1 250 cm-1)波段范围内的吸光度谱作为仿真实验的原始数据。 图2(a)是EPA数据库中八种气体在温度为25 ℃，光程为3 m时所测的FTIR吸光度谱原始数据，每种气体各有四条不同浓度下的谱线(其中两条谱线对应浓度约为100×10-6，两条谱线浓度约为500×10-6)，而这四条谱线的吸光度值与对应浓度值之间不成正比，证明了EPA数据库中利用FTIR实测得到的VOCs气体吸光度与对应浓度值之间存在着非线性关系。 在不考虑气体间的相互影响时，多组分气体混合物在某一波数处的吸光度值等于各个组分在该处的吸光度之和，将八种VOCs气体不同浓度下的吸光度谱进行随机组合，共得到65 536种混合气体吸光度谱。 图2(b)是将8种VOCs气体吸光度谱进行加和得到的一个混合气体样本的吸光度谱样本。 式(10)是利用单一气体谱线人工合成多组分混合气体吸光度谱的计算公式，其中Ai混合气体在第i个波数处的吸光度，Aij是指第j种气体在第i个波数处的吸光度。

(10)

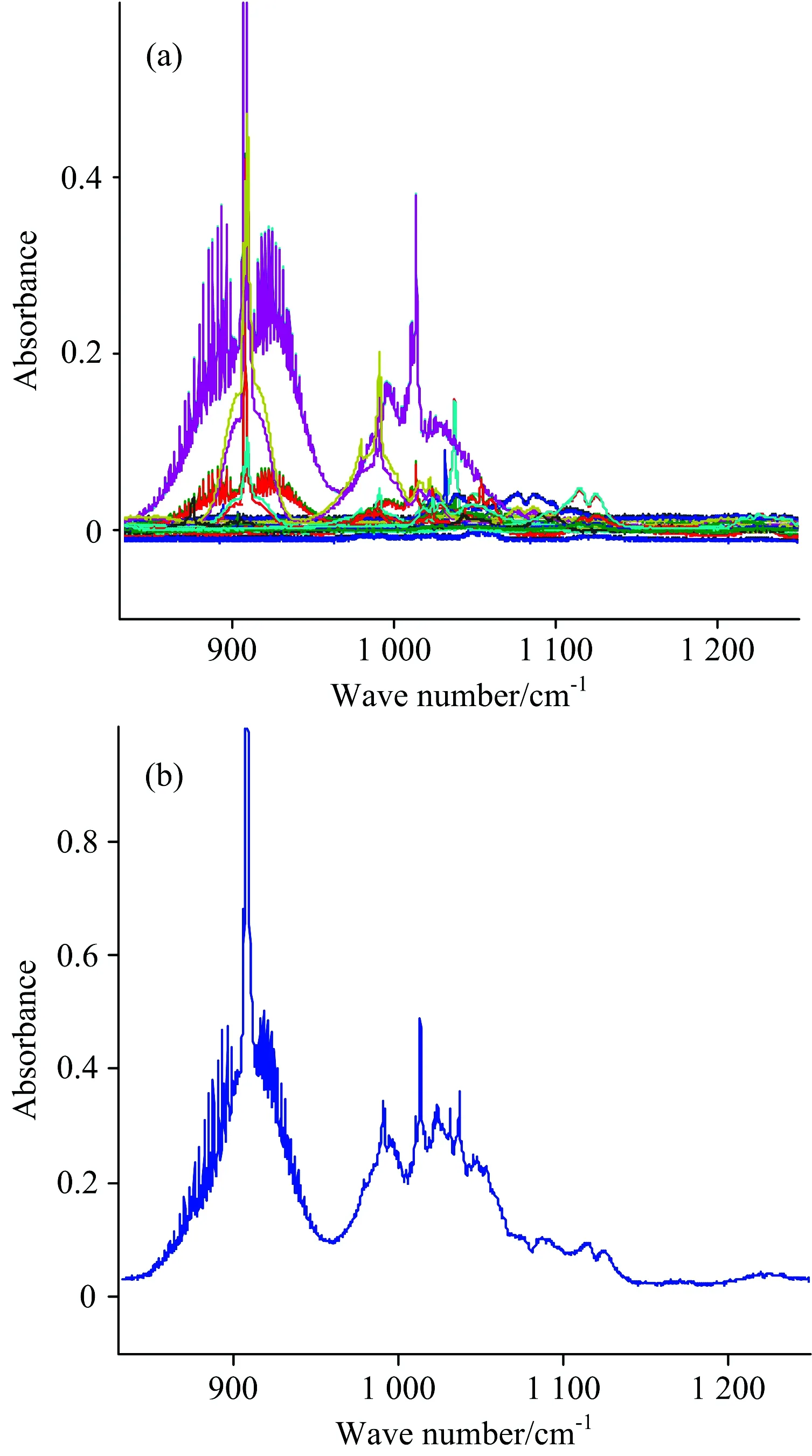
图2 波长在8～12 μm范围内的吸光度谱

2.2 数据预处理

数据预处理是通过对谱线原始数据进行降维来降低计算的复杂度，包括积分提取和主成分提取。 为了降低谱线噪声对于反演精度的影响，采用较为普遍的梯形法提取吸光度值在各波数点前后10个波数范围内的积分强度来代替信号较弱的吸光度值。 式(11)是梯形法计算积分强度公式，将待积分区域分成n段，每段间隔为Δν,Ai是第i个波数处的吸光度值。

(11)

采用主成分分析法(principal components analysis，PCA)对积分提取后的光谱矩阵进行主成分提取。 PCA是指通过分解原始矩阵，从而提取出能够表征原始矩阵数据特征、且不失去主要信息的主成分矩阵作为新矩阵。 式(12)是矩阵X(n×k)的PCA分析式，其中X是原始矩阵，t是得分向量，p是载荷向量，E是描述X从pf到pk的变化的误差矩阵。

(12)

为了确保样本的随机性，每次随机选取一定数量且不重复的混合气体吸光度谱进行DNN回归预测。 图3(a)为随机抽取的5 000条不同混合气体的吸光度谱； 图3(b)为对5 000条混合气体的吸光度谱积分提取后得到的结果，可以看到积分提取强化了谱线特征，光谱维度由3 457维降低到了406维； 图3(c)是对积分提取后的光谱矩阵进行主成分分解的结果，可以看到误差矩阵E对光谱矩阵的影响很小，而影响误差矩阵E的主要因素是测量噪声，因此忽略矩阵E不会造成原始数据中主要的有用信息丢失，同时可以在一定程度上减弱噪声的影响； 图3(d)是主成分提取后的光谱矩阵，光谱维度406维降到了30维。 根据主成分提取规则，一般情况下按特征值贡献率从大到小排列，当累计贡献率达到80%时，选取这些特征值的特征向量作为主成分，这里由于8种VOCs气体的红外光谱严重混叠，为了提高网络对不同VOCs气体的识别能力，选择累计贡献率达到99.9%作为主成分提取标准，提取原始矩阵的载荷向量数为30。

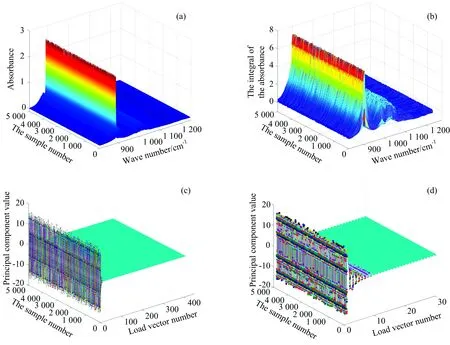
图3 5 000组样本的数据预处理

2.3 深度神经网络浓度反演

本程序均由MATLAB2018a编写而成，所有计算均在Dell OptiPlex7050计算机上进行。 使用训练样本训练神经网络，使得经过训练的网络可以充分学习混合气体的吸光度谱与对应每个组分浓度之间的特定关系，从而可以根据待测样本的吸光度谱预测每种VOC的浓度，过程可分为网络构建、网络训练和网络预测。

将5 000组经过预处理的样本，随机选择4 000组作为训练样本，1 000组作为预测样本。 将训练样本中的光谱矩阵作为DNN的输入，对应八种气体的浓度矩阵作为DNN的输出。 对训练样本的输入输出进行归一化处理，图4是训练样本归一化的结果。 所选用归一化函数为

xk=(xk-xmin)/(xmax-xmin)

(13)

利用深度神经网络模型进行浓度反演，需要构建合适的深度神经网络模型、选择合适的网络参数。 通过优化，确定了以下参数来进行构建DNN模型。

(1)输入、输出： 输入矩阵是经过预处理后的混合气体光谱矩阵，维数为30，因此输入层的节点数为30； 输出矩阵是混合气体对应的各组分浓度矩阵，维数为8，因此输出层的节点数为8。

(2)隐藏层层数： 隐藏层层数越高，泛化能力越强，预测精度越高，但是网络复杂度较高，训练时间较长。 在选择隐藏层层数时需要从网络预测精度和训练效率两方面综合考量，在网络精度达到要求且趋于稳定的情况下，选择较少的层数来加快训练速度。 从网络预测精度和训练时间两个方面比较其他网络参数相同时，不同隐藏层层数下的深度神经网络性能，表1列出了不同隐藏层层数下10次预测结果的平均值。

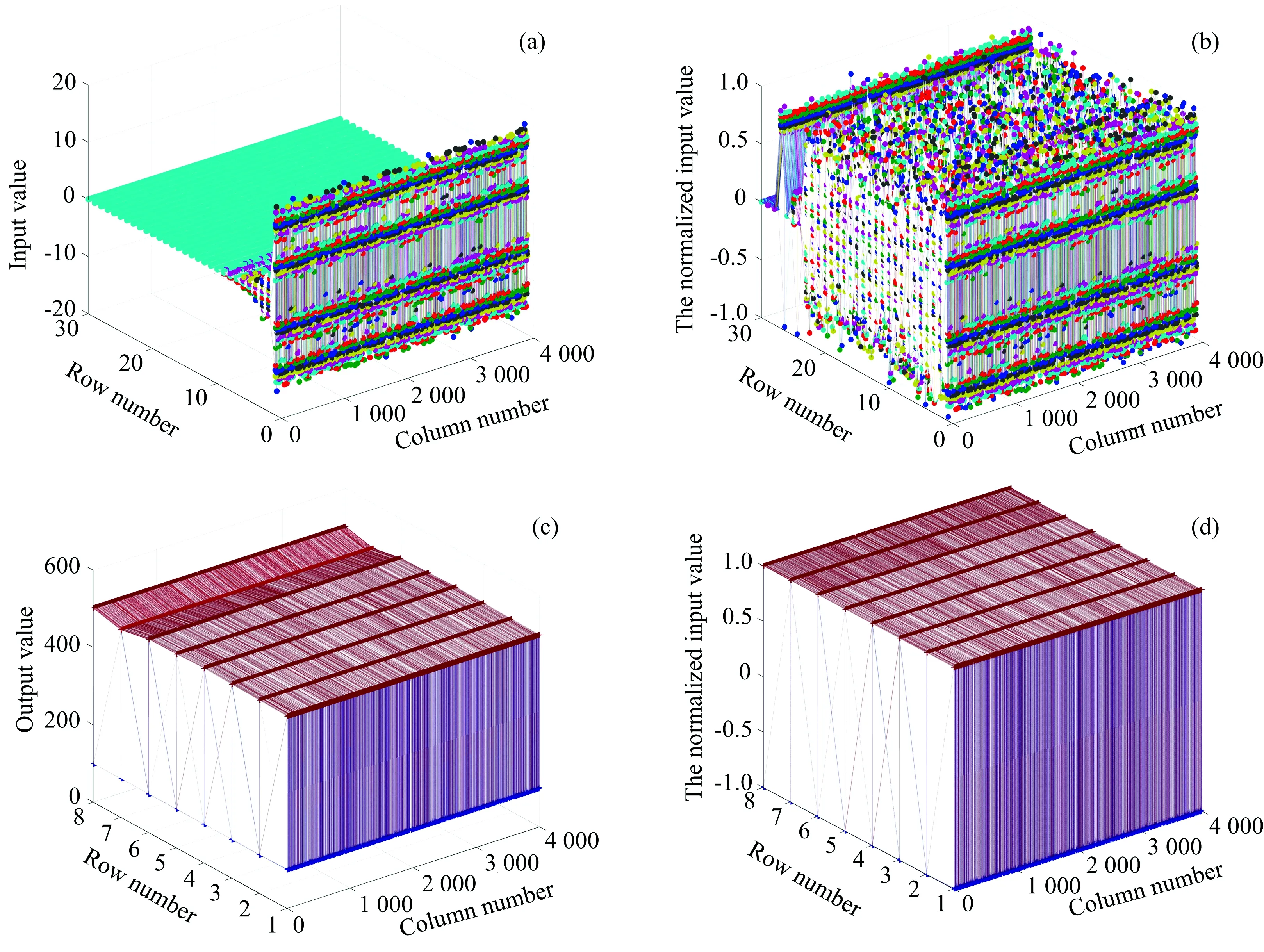
图4 训练样本的输入输出

表1 不同隐藏层层数下的深度神经网络预测结果

可以看到隐藏层层数越多，训练时间越长； 在一定范围内，隐藏层层数越多，网络预测精度越高，当隐藏层层数过多时，会出现“过拟合”现象，预测误差变大。 因此从预测精度和训练时间两方面综合考虑，选择隐藏层层数为3的网络模型用于网络训练。

(3)隐藏层节点数： 确定了隐藏层层数后，用试凑法来寻找最佳隐藏层节点数，表2是不同隐藏层节点数下10次预测结果的平均值。

可以看到，当某个隐藏层的节点数大于输入层节点数时，网络的预测误差较大，因此隐藏层节点数必须小于输入层节点数； 当隐藏层节点数逐层递减时，网络的预测误差较小。 满足上述两个条件时，网络的预测误差值较小，结合表2中的结果，选择25，15，10作为三个隐藏层神经元的最佳节点数。

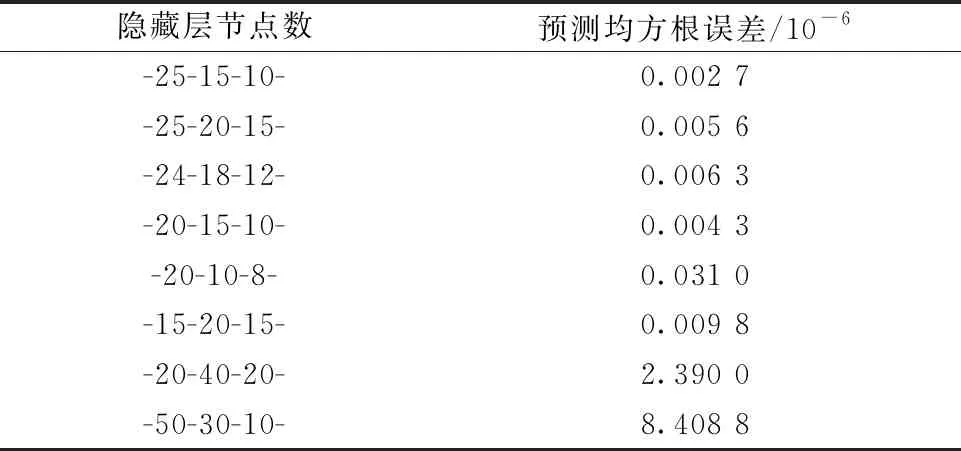
表2 不同隐藏层节点数下的网络预测误差

选择sigmoid函数作为隐藏层的神经元激活函数、ReLU函数作为输出层的神经元激活函数； 目标损失函数为均方差函数； 采用变学习速率法，最大学习速率为0.2，最小学习速率为0； 最大迭代次数设为1 000； 阈值ε设为0。 用训练样本训练经过优化得到的深度神经网络模型，然后用训练好的神经网络预测各待测样本的输出，输出结果反归一化后得到反演出的各组分浓度值。

2.4 误差分析

将预测出的各组分浓度与真实浓度作差可以得到预测结果的实际误差，图5是1 000组预测样本的实际误差图。 可以看到实际误差的范围在-0.004×10-6～0.004×10-6之间，证明了该深度神经网络对每个样本的每种气体都有着较好的预测结果。

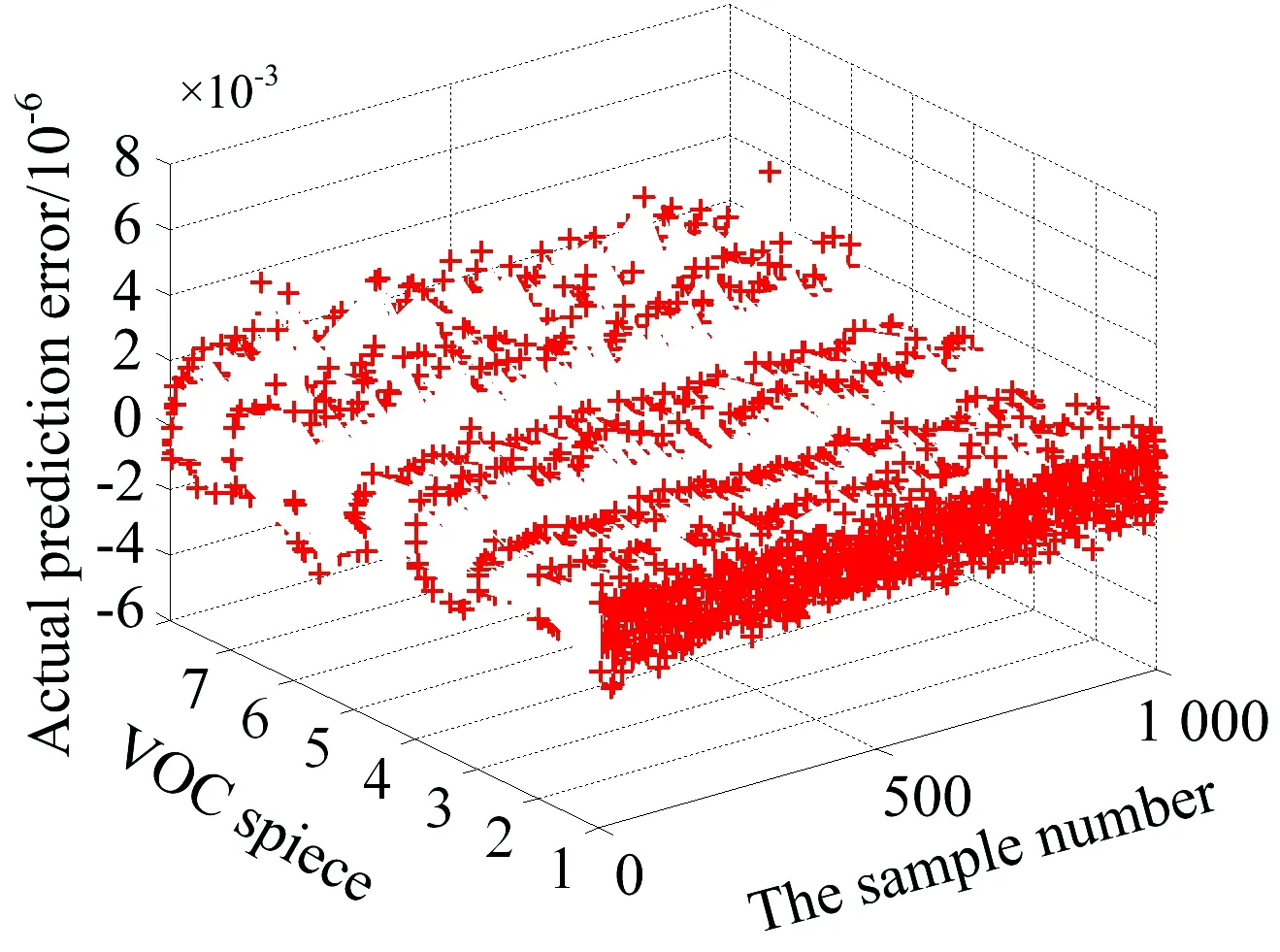
图5 DNN反演的实际预测误差

图6(a)是每种VOCs预测浓度(共1 000个样本)的均方根误差，图6(b)是每个样本预测浓度(共8种气体)的均方根误差。 每种VOCs气体的预测误差都小于0.005×10-6，表明DNN可以很好地用于多组分分析； 每个样本的误差均小于0.006×10-6，表明了DNN预测模型具有较高的稳定性； 1 000组预测样本的均方根误差为0.002 7×10-6，表明利用DNN模型进行多组分VOCs浓度反演具有较高的精度。

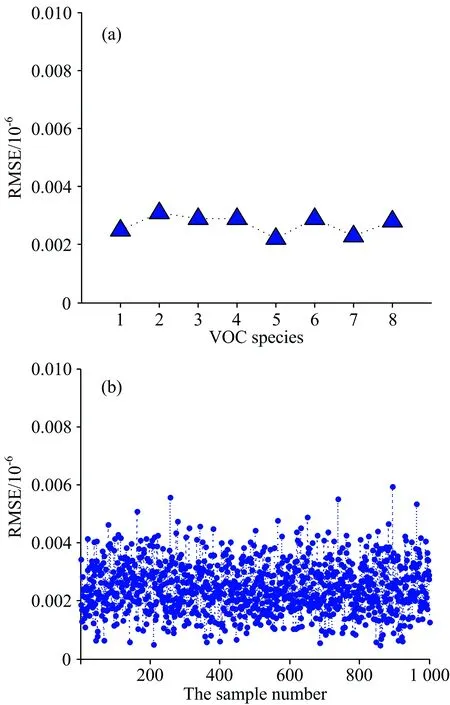
图6 预测结果的均方根误差

表3是在不同样本数下利用DNN进行浓度反演得到的各组分浓度的误差。 表中的每一列代表随机抽取的样本数量，其中4/5用作训练样本，1/5用作预测样本，每一行为各个组分在不同样本数下训练测试得到的均方根误差。 可以看到，当训练样本充足时，DNN可以得到较好的预测结果，并且预测精度随着样本数量的增加不断提高。 在实际应用时，可根据VOCs监测在精度方面的需求，选择合适的样本数量进行训练。 当对精度要求较高时，可选择用更多不同种类的样本训练神经网络，使网络可以充分学习； 当满足精度要求时，可选择合适的样本数量来减少网络计算复杂度，提高反演效率。

表3 每种VOC气体在不同样本数下的均方根误差

2.5 DNN与ANN精度对比

通过优化参数，建立30-11-8的单隐藏层人工神经网络模型，选择隐藏层神经元激活函数为sigmoid函数，输出层神经元激活函数为ReLU函数，最大学习速率为0.2，最小学习速率为0，附加动量项为0.2，最大迭代次数设为1 000。 在不同样本数下进行浓度反演，对比验证DNN算法模型的精度。 图7是DNN和ANN浓度反演结果的误差随着样本数量变化的曲线图。

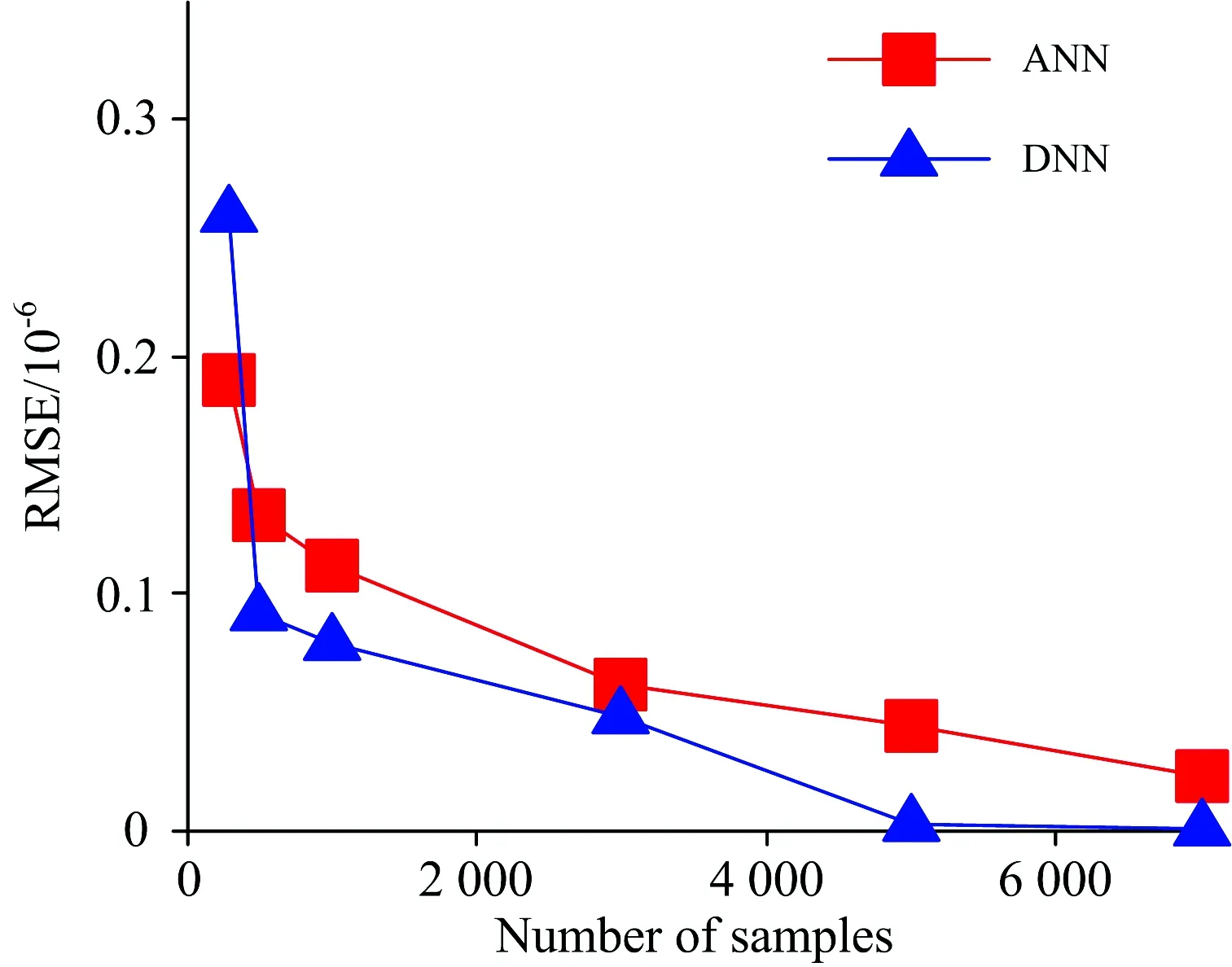
图7 DNN与ANN在不同样本数下的精度对比

由图7可以看出，当样本数量为300时，DNN的误差为0.26×10-6，ANN的误差为0.19×10-6，这是因为当样本数量较少时，DNN网络模型相较于ANN模型网络更为复杂而不能够得到充分训练，所以预测精度低于ANN； 随着样本数量增多，ANN和DNN的精度均呈现上升趋势，此时充分得到训练的DNN模型对数据的非线性特征的拟合优势就体现出来，网络预测精度相较于ANN模型有了大幅度提高，证明了深度神经网络在基于红外光谱的多组分VOCs浓度反演方面有着很好的应用前景。

3 结 论

从EPA数据库中选取了八种有毒挥发性有机物8～12 μm范围内的吸光度谱，根据Beer-Lambert定律进行混合，经过积分提取、PCA降维等预处理后作为输入，各组分浓度作为输出，建立了30-25-15-10-8的深度神经网络模型进行多组分易挥发性有机物浓度反演的研究。 实验显示，深度神经网络无需利用先验知识人工提取特征，可直接从经预处理后的原始数据中学习特征，比传统的人工提取特征更为简单； 当训练样本数过少时，深度神经网络无法充分学习，训练误差较大，精度低于浅层的人工神经网络，但随着训练样本数量的增加，DNN的精度不断提高，样本数量为5 000时反演精度达到了0.002 7×10-6，相较于只有一个隐藏层的人工神经网络有了明显的提高； 在多组分气体反演时，DNN同时对每种气体都能达到较好的预测精度。 结果证明，在训练样本充足时利用深度神经网络对多组分VOCs进行浓度反演的结果精度较高，相比单隐藏层的人工神经网络，能更充分地学习数据特征，具有更强的非线性拟合能力和稳定性。