近红外光谱的选择比率竞争群体分析的变量选择算法

王玉喜，贾振红*，杨 杰，Nikola K Kasabov

1. 新疆大学信息科学与工程学院, 新疆 乌鲁木齐 830046 2. 上海交通大学图像处理与模式识别研究所，上海 200240 3. Knowledge Engineering and Discovery Research Institute, Auckland University of Technology, Auckland 1020, New Zealand

引 言

近几年来，近红外光谱(NIR)分析在石化、制药、环境、临床、农业、食品和生物医学等领域得到了广泛的应用； 有时，不同样品的光谱包含的信息非常相近，变量提取困难。 灵敏、快速和准确的提取相关变量来预测样品的化学成分是化学计量学的重要内容。 一般来说，近红外光谱技术与多变量技术结合用于对相关物质的定性或定量分析。 在光谱化学计量学中通常遇到的是具有大量波长变量和相对较少样本的光谱数据情况，在这种情况下建模具有过度拟合的高风险，并导致多变量校准模型不良或低效的预测结果。 多变量分析中的变量选择是一个非常重要的步骤，因为消除无关或无信息变量和降低数据维度不仅可以简化校准建模，并在准确性和鲁棒性方面也能改进预测结果。

鉴于变量选择带来的益处，基于不同策略的变量选择方法已被大量提出。 这不仅包括传统经典的方法，如前向选择和后向消除[1]; 惩罚性方法，如最小绝对收缩和选择算子(LASSO)[2]，弹性网和最小角度回归(LARS)[3-4]; 智能学习算法，如遗传算法(GA)[5]，蚁群优化(ACO)[6]和粒子群优化(PSO)[7]。 还有一些基于不同的变量排列标准的方法，如回归系数[8]，投影中的变量重要性(VIP)和选择性比率(SR)[9]，蒙特卡罗无信息消除(MC-UVE)[10]和子窗口置换分析(SPA)[11]。 随着模型群体分析(MPA)思想的发展，在此基础上提出了一些新的算法如竞争自适应重加权采样(CARS)[12]，变量迭代空间收缩法(VISSA)[13]，搜索空间的交替通缩和膨胀法(ADISS)[14]，自加权变量组合集群分析法( AWVCPA)[15], 变量组合群体分析(VCPA)[16]，自举软收缩法(BOSS)[17]等。

本算法继续了MPA(模型集群分析)策略算法的优点，首先从大量的子模型中提取有用信息，避免单个模型的结果或参数不可靠性。 其次保留变量间的协同与组合效应，在随机采样优化中产生随机变量的组合。 并通过收缩策略逐步消除无关变量，保留信息变量。 同时还规避掉了此策略算法需要大量的迭代和循环、算法效率低、收敛速度慢的缺点。 本算法将时间效率和变量选择效果考虑在内，即降低时间成本，同时能够保证选择出近红外光谱中的信息变量，消除数据集变量中的无信息和干扰变量，增加光谱模型的可靠性与稳定性。 还考虑了关键变量以回归系数绝对值定义的问题，MPA策略下的算法大部分以回归系数绝对值作为变量重要性的依据，以采样技术(如二进制重采样)通过收缩策略逐步消除无关变量，由于回归系数的绝对值并不总是反映变量重要性的真实信息，会受到噪声等诸多因素的影响[18]，从而会对变量选择算法造成不良影响，而以SR(选择比率)得分值定义的重要变量会更有优势，可以消除噪声诸多因素对光谱数据的影响。 啤酒酵母底物数据集在采集光谱时在1 100～2 500 nm处存在噪声，本算法可以消除噪声的影响，即采用选择比率可以定位到信息变量区域，减弱噪声因素和无关变量对变量选择算法的影响，减少噪声和无关变量被选入关键变量的可能。

1 实验部分

1.1 数据来源

1.1.1 啤酒数据集

啤酒近红外光谱数据集[19]是使用NIR Systems Inc.收集25 ℃下的分散近红外数据(包括视觉区域)。 并以2 nm的间隔在400～2 250 nm范围内收集。 对于该研究，选择了NIR区域1 100～2 250 nm(576个数据点)。 原始提取物浓度表明酵母发酵成酒精的底物被认为是研究感兴趣的化学性质，并用化学方法测量其浓度。 通过对提取值进行分类，运用Kennard-Stone分类法选取其中的40个样本的近红外光谱数据和化学值数据作为校正预测模型集，剩余的20个样本的近红外光谱数据和化学值数据作为预测集检验模型。

1.1.2 小麦蛋白数据集

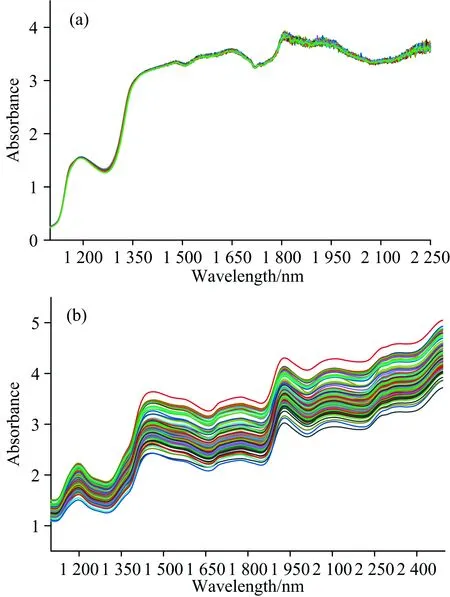
图1 (a)啤酒光谱; (b)小麦蛋白光谱

1.2 模型校验

假设大小为n×p的数据矩阵X包含行中n样本和列中的p变量，并且大小为n×1的向量y表示所测量的感兴趣属性。 在建立PLS模型时，X和y都以均值中心化处理。

模型评价参数的作用是评价通过校正集样本建立的预测模型可靠性。 在近红外光谱多元校正建模过程中，由相关系数Q2、预测均方根误差(RMSEP)和交叉验证均方根误差(RMSECV)对模型评价。 模型相关系数Q2越高，即越接近1越好。 RMSECV和RMSEP越小，即越接近0模型预测能力越强。

1.3 使用软件说明

使用的是一台通用联想计算机，内核为i5 3.2 GHz CPU，内存为4g，操作系统为Microsoft Windows 7。 所有计算均在MATLAB 2016a中进行。 数据可视化处理用Origin2016。

2 SRCMPA算法原理

将功能指数递减函数(EDF)的迭代次数和蒙特卡罗采样(MCS)次数设置为N。 每次随机MCS采样的采样比率为R。 使用上述设置，SRCMPA可以在每次迭代中分为四个步骤： (1)变量的子集使用固定选择比率的蒙特卡罗抽样随机建立。 (2)计算每个变量的SR得分值，为一个p维的得分值向量，并对其值排序，然后使用EDF强制消除排列靠后面的非信息或冗余变量，以变量保留比例ri=ae-ki, 即以EDF消除ri×p数量以外的靠后变量。 (3)标准化的SR分数作为每个波长和自适应加权抽样方法进一步消除变量的权重。 有较大权重的变量被保留的概率更大，而权重弱的变量竞争力较弱，并且在变量的群体内逐渐被消除。 (4)N次迭代后会获得N变量子集，并应用交叉验证以评估每个子集。 其中交叉验证的最小均方根误差的子集被选为最佳子集。

2.1 蒙特卡罗采样

蒙特卡罗抽样是一个用于分析复杂(多元变量)问题十分有效且应用广泛的重要统计工具，在每次采样运行中，样本和变量都分别随固定数量随机选择。 MCS在样本空间和校准集的可变空间中实现，以此获得若干个子数据集，并利用PLS等一些回归方法在每个子数据集建立子模型，进而形成模型空间。 利用统计分析方法可对每个子模型输出参数分析，来评价每个子数据集感兴趣的未知参数。

2.2 选择比率和回归系数

模型解释是偏最小二乘法(PLS)的大多数应用中的重要任务。 从作为潜在回归方法的性质看，偏最小二乘回归提供了一种多对多线性回归建模的方法，能够处理具有严重多重相关性高维度数据。 然而，使用潜在变量也会给模型解释带来困难。 这种困难是由于PLS构造的潜在变量不仅是为了最大化数据矩阵X和响应y的相关性，而且还同时尝试X解释方差的最大化。 因此我们无法使用诸如权重和负荷之类的模型参数来直接解释模型。 尤其是在受多种变异来源影响的分析数据中，当主要变异源与Y无关时，所解释的X方差的最大化可能会将无关信息带入PLS模型。 因此基于这些参数对PLS模型和变量重要性解释并不容易。

2.2.1 回归系数

对于回归系数(Beta)重要变量的选择，直接的策略是量化回归系数周围的置信区间，但在PLS线性模型下，响应向量y依赖其正交投影到由X的列向量所生成的子空间上的投影矩阵，即帽子矩阵。 PLS回归系数也没有用于不确定性的封闭分析形式。 因此，重采样技术通常用于确定置信区间。 各种重采样技术可用于PLS回归系数，但并没有一种方法可以在模型中提供变量重要性的直接排序。 通常以回归系数的绝对值作为指导，但回归系数的绝对值并不总是反映变量重要性的真实信息，还会受到噪声等诸多因素的影响。

另外，如果选择跟团游，超过70岁以上老人，一般要求有可照顾老人家属陪同，对于具体参团目的地暂时没有限制，但建议游客选择行程轻松、舒适，不过于劳累或疲惫的线路，此外不建议参加有较大安全风险的产品，例如水上项目、高风险运动类的产品。

2.2.2 选择比率

关于选择比(SR)[21]，在给定PLS的回归系数向量bpls条件下，TP分数是通过以X的行在归一化回归系数向量上的投影来实现的，tTP是与预测值成比例的。 对于载荷PTP是通过投影X的列到分数向量得到的

tTP=Xbpls/‖bpls‖

(1)

(2)

解释和残差方差可以通过变量矩阵X和投影(TP)分数和载荷来计算

(3)

(4)

Si, res=‖eTPi‖2,i=1, 2, …,p

(5)

由式(4)和式(5)确定选择比被定义为对于第i个变量的解释的方差Si, exp与每个变量的残差方差Si, res之比

SRi=Si，exp/Si, res,i=1, 2, …,p

(6)

F检验定义为高辨别能力的可变区域间的边界和非兴趣区域。 为了确定哪一个变量具有高辨别能力和拒绝零假设(解释和剩余方差是相同)，其值必须超过F分布的临界值Fcrit

SRi>Fcrit=F(α,N-2,N-3)

(7)

应用SR来重新量化X方差，以通过目标旋转或正交滤波策略改进对变量重要性的解释。 目的是分配与X和y之间的协方差成比例的信息，同时隔离正交无关变化。 参考文献中提出了确定变量重要性的临界阈值。 在SRi中评估F分布的N-2和N-3自由度。 这项工作中，选择了F检验(95%)标准选择候选目标。

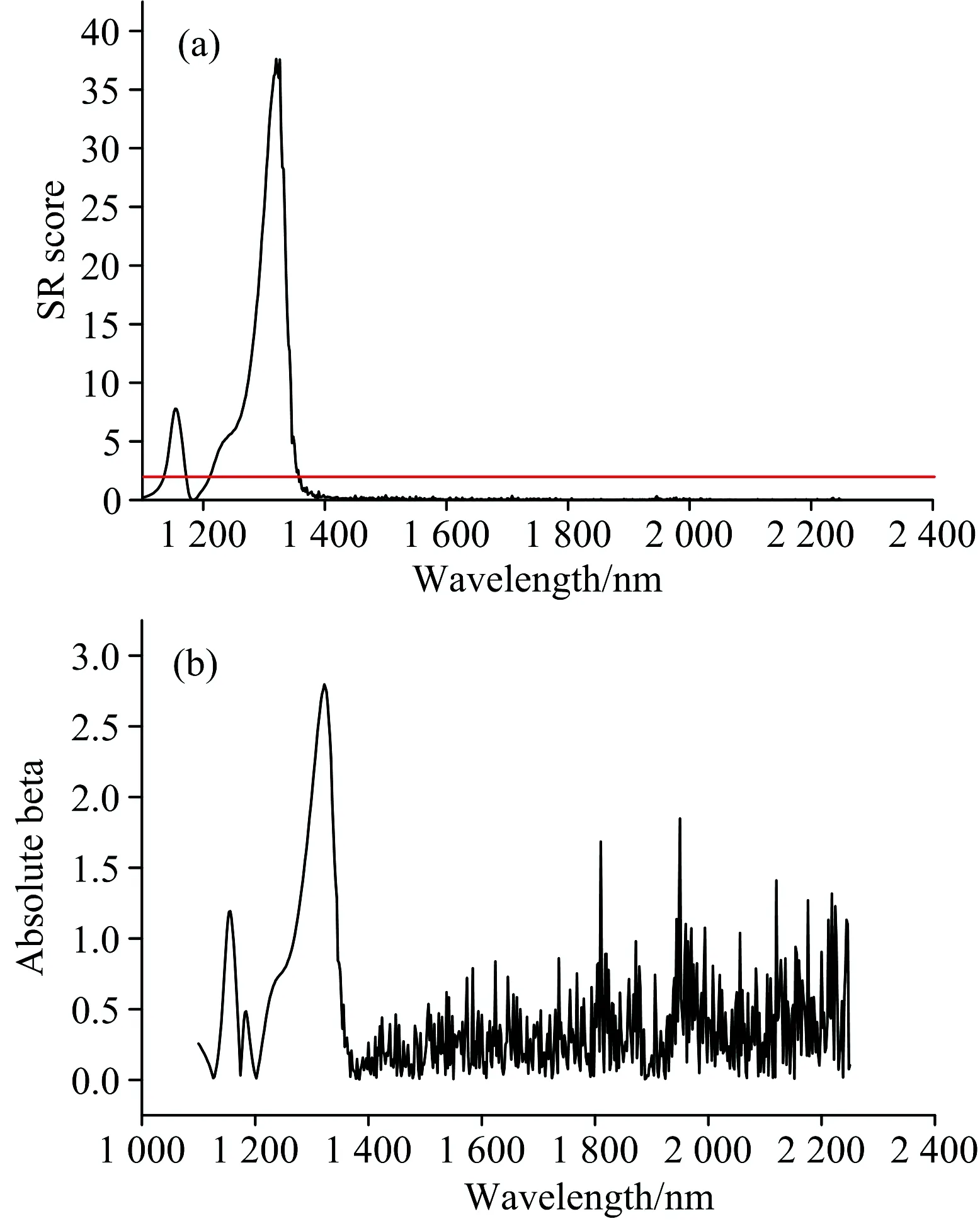
图2 啤酒光谱数据集以选择比率和回归系数绝对值的变量重要性图示

Fig.2Thevariableimportanceofthebeerspectraldatasetwiththeselectionratioandtheabsolutevalueoftheregressioncoefficient

The red line represents the threshold of important variable

(a): Selectivity ratio scores;(b): Absolute value of regression coefficient

图2中SR定义的重要变量的曲线比较平滑，干扰较少。 而回归系数的绝对值定义的重要变量还包括了大量无关变量的存在，曲线出现大量的干扰变量，这会对以此为变量重要性的变量选择算法会造成非常大影响，会大大增加无关和干扰变量被选入关键变量的可能性。 并且SR定义的重要变量区域与啤酒数据集酵母底物化学性质的重要变量吻合，在啤酒光谱数据集中1 100～1 350 nm区域对应O—H拉伸键振动的第一倍频和C—H拉伸键的第二倍频。 它符合啤酒光谱集所要研究的感兴趣的酵母底物的化学性质。 所以SR作为变量选择方法的重要变量定义更具有优势，它可以将噪声影响剔除掉。

SR=[sr1,sr2, …,srp]T是p维SR分数向量, 其中SR向量里的值都大于临界阈值，SR分数中第i个元素sri反映第i个波长对于y贡献。 我们评估每个波长的重要性，将SR进行排序，排名越靠前的变量越重要。 我们在这里对于评估每个变量，还要定义归一化的权重用于自适应抽样来竞争选择重要变量

(8)

另外注意的是被消除的波长的权重被强制变为零，并使得权重向量总是p维的。

2.3 功能递减函数和自适应竞争抽样

EDF被用来模仿“物竞天择”原则。 EDF的选择可分为两个阶段[12]，第一阶段被名为“快速筛选”，有很多不重要的变量会被迅速消除，对于指数递减函数在开始阶段对应的消除比率比较大，消除无信息力度比较大。 第二阶段被名为“精细筛选”，随着无信息和不重要的变量的减少，指数递减函数对应的消除比率越来越小，且接近于0，是为了避免错误的消除关键变量。

在基于EDF的强制波长减少之后，SRCMPA中采用自适应重加权采样(ARS)以竞争方式进一步消除波长。 采用自适应采样进一步消除较弱权重的变量，这类似于进化论中的“适者生存”。 权重越大的变量具有较大的概率被保留，而其较弱权重的变量竞争性比较差，在变量种群会被逐渐淘汰。

3 结果与讨论

基于Kennard-Stone(KS)方法将所有数据集分成校准集和独立测试集。 KS方法旨在通过最大化每对所选样本之间的欧几里德距离来覆盖多维空间。 校准集用于变量选择和拟合优度，独立测试集用于验证校准模型以进行预测。 校准集进行变量选择时，用交叉验证。 此外，为了评估SRCMPA的性能，我们将与优秀方法CARS，BOSS，VISSA进行比较。 通过交叉验证与蒙特卡罗采样次数之间的参数优化选择，对于CARS和SRCMPA的蒙特卡罗采样运行的次数都选择为300，并且蒙特卡罗采样比率都为0.9。 BOSS算法的二进制采样次数为1000，优秀子集占优比率为0.1。 VISSA算法二进制采样次数为5000，子集选择比率为0.05。 对于所有方法，最大潜在变量限制为10，潜在变量的数量由10倍交叉验证确定。 在建模之前，每个数据集将被均值中心化。 所有方法进行50次运行以获得统计结果并公平地比较这些方法。

3.1 SRCMPA算法的变量提取结果

在图3(a)中，啤酒近红外光谱所选中的信息变量区域主要分布在1 100～1 350 nm之间，这个区域与O—H键伸缩振动第一倍频区一致。 这与本研究感兴趣的酵母底物的化学性质相一致，说明本方法SRCMPA能够很好地消除无信息或干扰变量，达到较好的选择信息变量的目的。

在图3(b)中小麦蛋白数据集中所选的波长变量集中在1 100～1 400 nm的区域，这部分区域属于C—H拉伸模式的第二倍频和O—H的拉伸模式的第一倍频。 光谱特征和官能团的振动模式有关。 样品中存在的有机物在NIR区域具有明显的光谱特征，对应于几个官能团相对强烈的组合模式的吸收强度。 本算法选择了相关的信息区域变量，达到消除无关或无信息变量的目的，这也与我们选择研究的小麦蛋白化学有机物的性质相一致，说明本算法SRCMPA有很好的选择特性。

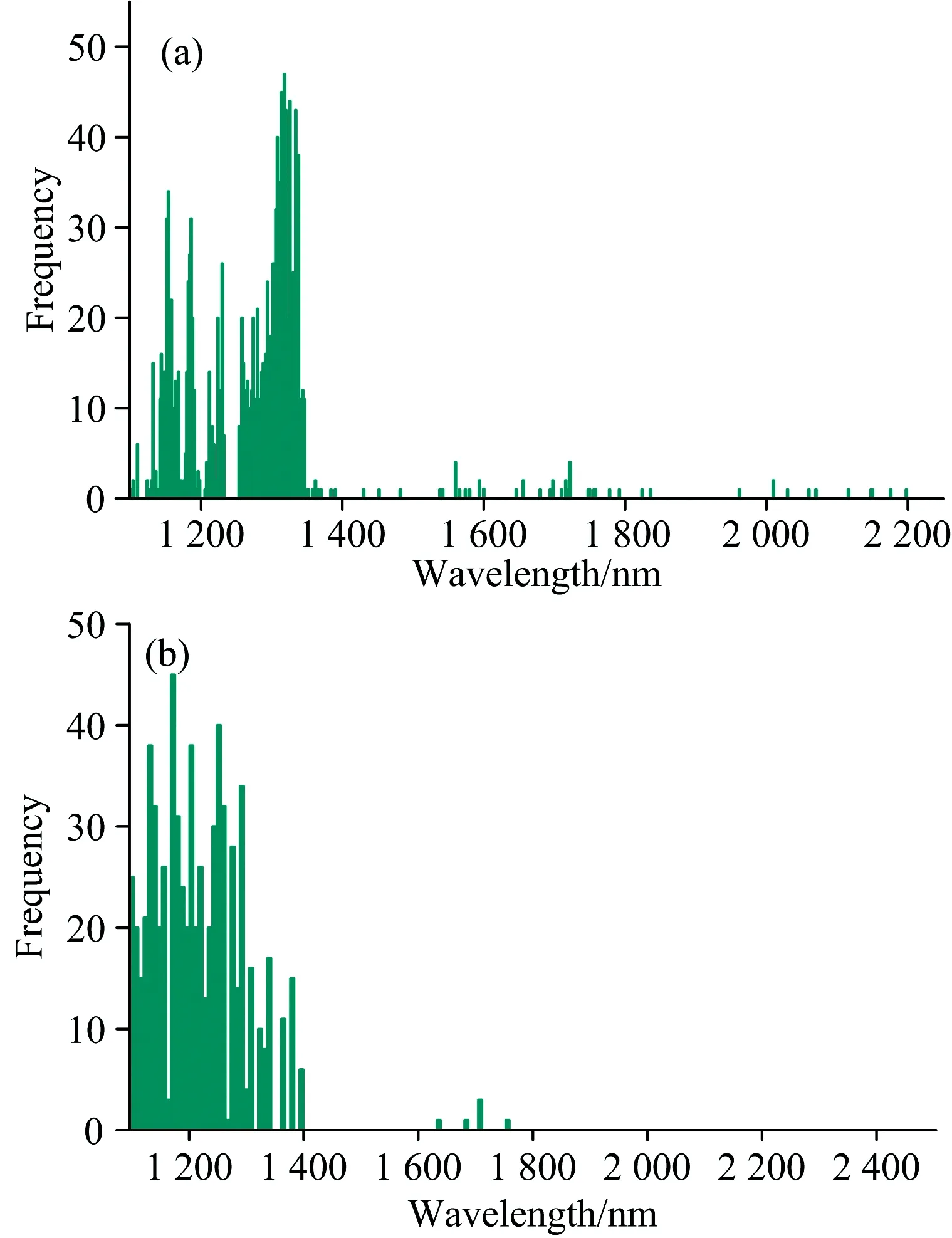
图3 SRCMPA运行50次后(a)啤酒光谱变量被选取的频率和(b)小麦光谱变量被选取的频率

Fig.3(a)Frequencyofbeerspectralvariablesselectedand(b)frequencyofwheatspectralvariablesselectedafterrunningSRCMPAfor50times

3.2 不同方法建模结果与统计分析

将均值中心化的啤酒和小麦近红外光谱数据在相同条件下分别采用4变量选择方法(CARS，VISSA，BOSS，SRCMPA)进行50次变量选择选取特征波长，然后利用PLS建立预测模型。 对模型输出结果平均值和标准差来说明。 表1和表2分别是啤酒中酵母浓度和小麦蛋白以不同方法建模后的结果。 本算法在啤酒数据集的运行结果，相较于全光谱PLS模型，变量个数已由567个减少到42个左右。 并且模型的RMSECV由0.622下降到0.115，RMSEP由0.823减少到了0.263左右，预测精度分别提高了81.5%和68.0%。 Q2_CV和Q2_test也分别由0.940, 0.852提高到了0.994和0.995，啤酒酵母底物数据集在1 100～2 500 nm内采集时存在噪声，本算法消除了噪声的影响，使得建模效果要比其他的算法更有优势。 本算法在小麦蛋白数据集的运行结果，相较于全光谱PLS模型，变量个数已由175个减少到18个左右。 并且模型的RMSECV由0.607下降到0.292，RMSEP由0.519减少到了0.234左右，预测精度分别提高了51.9%和54.9%。 Q2_CV和Q2_test也分别由0.748, 0.774提高到了0.931和0.839。

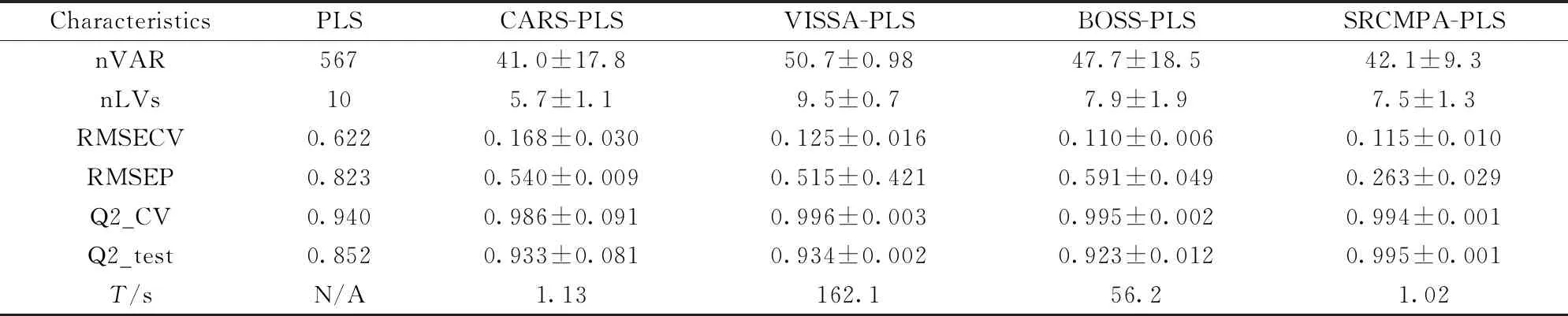
表1 不同建模方法对啤酒中酵母浓度的预测结果

注： nVAR: 选择变量数； nLVS: 潜在变量数； RMSECV: 交叉验证均方根误差； RMSEP： 预测均方根误差； Q2_CV: 交叉验证相关系数； Q2_test： 测试集的相关系数；T/s: 运行50次的平均时间； 所有的统计结果均为50次运行的平均值±标准差，下同

Note： nVAR: Number of variables; nLVs: Number of latent variables; RMSECV: Root-mean-square error of cross-validation; RMSEP: Root-mean-square error of prediction; Q2_CV: Coefficient of determination of cross-validation; Q2_test: Coefficient of determination of test set;T/s： Average time for 50 runs; All statistical results are the mean values±standard deviations over 50 runs, the same below

表1和表2说明所有变量选择方法的建模结果都优于全光谱建模，变量选择是十分必要的，可以剔除无信息或干扰变量，消除全光谱建模时的过拟合或不可靠的问题。 对比本算法SRCMPA与CARS-PLS，VISSA-PLS，BOSS-PLS可知，本算法在建模的预测与交叉验证的统计结果上，总体都有最佳的结果，并且在算法运行时间效率上也是最佳的。 可以通过节省大量的时间成本，来达到快速建模的目的，预测结果也同时得到保障。 SRCMPA-PLS在啤酒数据集的预测均方根误差(RMSEP)0.263，比CARS-PLS，VISSA-PLS, BOSS-PLS的RMSEP都要低，预测的相关确定系数(Q2_test)0.995, 比CARS-PLS，VISSA-PLS, BOSS-PLS的都要高，凸显了本算法的优势。 同样在小麦蛋白数据集上模型预测也都有良好的结果。 VISSA-PLS和BOSS-PLS虽然可以达到选择信息变量建模提高效果的目的，但效率低，需要非常多的时间消耗在选择变量步骤上面。 近红外光谱分析也要考虑到时间成本问题，快速有效的分析模型对现实应用十分重要。

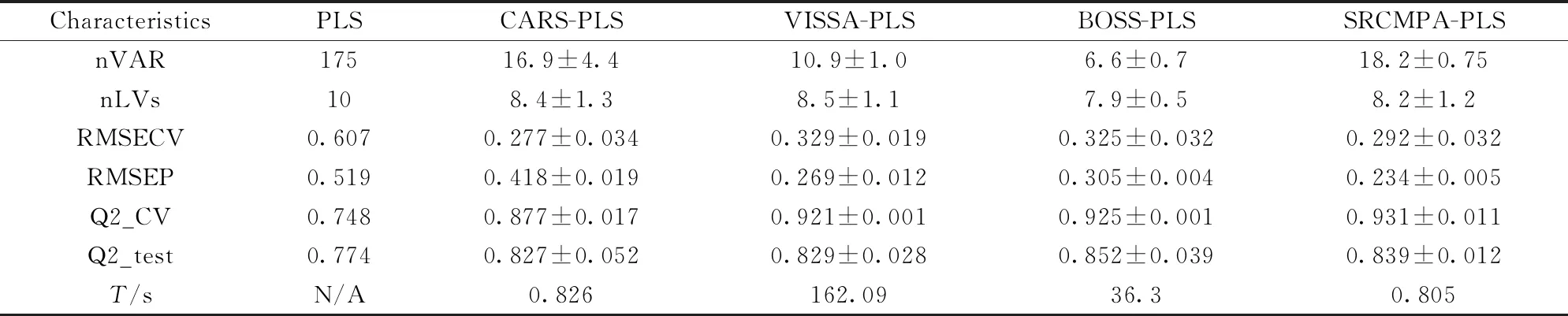
表2 不同方法小麦蛋白的预测结果

4 结 论

提出了一种新的变量选择方法SRCMPA，该算法结合了选择比率，自适应加权采样和模型群体分析(MPA)，变量排列和指数递减函数(EDF)竞争的方法。 CARS，VISSA和BOSS都以PLS的回归系数作为重要信息变量思路，在啤酒和小麦蛋白两种真实光谱的建模情况下，总体效果都不具备SRCMPA算法的优势。 本算法规避掉了从PLS模型以回归系数作为提取重要信息思路的弊端，而采用新的重要变量表示方法选择比率。 并且VISSA和BOSS算法都会在变量选择时花费较多时间，效率比较低，而本算法同样解决了时间效率上的问题。 证明了SRCMPA能够消除无信息变量和进行波长选择以构建高性能校准模型。