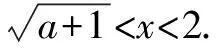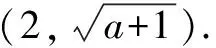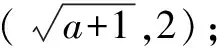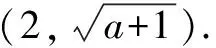续谈分类讨论

吴日明

(安徽省合肥市一六八中学 230601)

一、由题干的限制条件导致的分类讨论

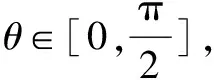
分析：因为题中θ的限制范围，进而cosθ有相应的约束范围，导致对a的相应讨论.

解析令h(θ)=cos2θ+2asinθ-2a-2=-sin2θ+2asinθ-2a-1.

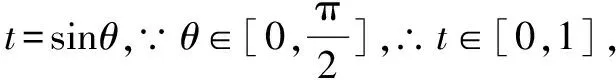
由二次函数性质，图象进行分类讨论得：

(1)若0≤a≤1，只需要h(a)<0，解得a∈[0,1].

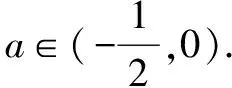
(3)若a>1，只需要h(1)<0，显然成立，所以a∈(1,+∞).

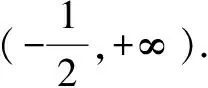
反思三角函数问题中，角的范围要重视，本题换元令t=sinθ，务必抓住t的范围，引发a的三种情况的分类讨论，使得a的范围才水落石出.

二、由公式定义的约束导致的分类讨论

例2设等比数列{bn}的公比为q，前n项和Tn>0(n=1,2,…)，(1)求q的取值范围；(2)设cn=bn+2-bn+1，记{cn}的前n项和为Sn，试比较Tn与Sn的大小．

分析本题中，由于数列{bn}是等比数列，特别要注意讨论公比q=1与公比q≠1的情况．

解析(1) 因为{bn}是等比数列，Tn>0，可得b1=T1>0，q≠0.

当q=1时，Tn=nb1>0；

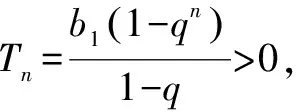
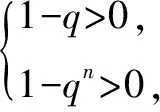
由于n可能是奇数，也可是偶数，故q的取值范围是(-1,0)∪(0,+∞)．

(2)由cn=bn+2-bn+1=bn(q2-q)，则Sn=(q2-q)Tn，

则Sn-Tn=(q2-q-1)Tn

因为Tn>0，-10，

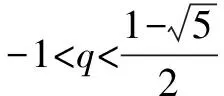
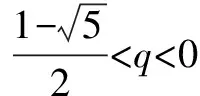
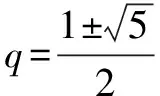
反思在解决数列通项与求和的关联问题中，特别要注意：n=1与n≥2的切实需要中的讨论，在解决等比数列的求和问题中，特别要注意对于公比q=1与公比q≠1的分情况讨论.

三、由运算的实际需求导致的分类讨论

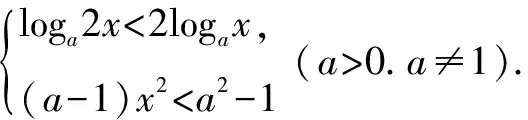
分析由于不等式中均含有参数a，其解的结果均取决于01.所以1为a的分类讨论标准.

解析(1)当0

(2)当a>1时,不等式组

(1)当1

当1

反思本题在不等式的求解化简过程中，不等号方向是否改变，以及不等式组内各解的交集的产生中，进而必然引发a与1，a与3的大小的讨论与分级讨论，才可以条理分明，结论清晰.

分类讨论的实际需要与归因有很多，在中学数学问题思考解决中，能避免的的可以尽力避免，不能避免的就要注意分类讨论的科学，有效，精准.