基于BP神经网络的多GM计数器γ辐射定向测量算法研究

李国栋，陈法国，唐智辉，韩 毅，杨明明

(中国辐射防护研究院，山西 太原 030006)

在放射源搜寻作业时，常规的辐射监测仪表通常不具备辐射定向功能，需通过人工方式对关注空间进行网格化分割和巡测来获取放射源的方位信息。这种方法搜寻区域大、工作时间长，相关人员还可能会因此受到较多照射。为快速、准确地获取辐射源项的空间分布信息，国内外发展了多种γ定向测量方法和设备，主要有γ相机成像、多闪烁体设计[1]、屏蔽分割的多探头组件设计[2]、层状塑料闪烁体设计[3]、局部屏蔽的探测器结构设计[4]等，这些新型设备依其性能特点应用于不同作业现场使搜寻时间和搜寻区域大幅减少。本文仅针对放射源角度区间的识别需求，利用GM计数器探头结合十字铅屏蔽结构设计一种简易便携式放射源定向测量装置，以实时动态定位二维空间放射源角度范围，并基于神经网络反演放射源入射角度的算法方案，讨论不同算法模型的角度识别精度和抗干扰能力并利用137Cs源对样机进行功能测试。

1 定向装置设计及放射源定位原理

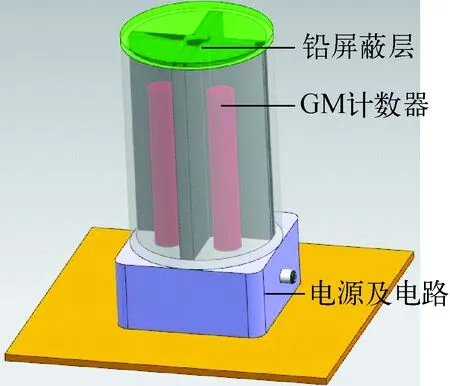
图1 定向装置结构设计Fig.1 Structure design of direction finder

铅屏蔽GM计数器定向装置为多探头组件设计，基于射线穿过结构化铅屏蔽层不同位置时衰减的差异性原理，采用1组尺寸、响应一致的GM计数器探测器监测各位置的计数响应，并根据其相互关系来反演射线的入射方向。图1为该装置设计示意图，4个GM计数器对称分布于坐标系4个象限距坐标轴2.5 cm处并编号1、2、3、4，中间采用等厚十字交叉的板状屏蔽体。考虑到尽可能满足宽能量范围射线探测，屏蔽体厚度选择为1 cm。屏蔽体径向宽度L需根据角度分辨的灵敏性需求后续进行调整。利用蒙特卡罗软件GEANT4模拟计算了不同能量γ射线在2π方向内入射时各探测器的剂量率响应，以x轴方向为0°基准，屏蔽体径向宽度设置为7 cm，选择其中0.2、0.662、1.3 MeV 3个能量为代表，装置模型4个GM计数器探测器响应的归一化结果如图2所示。

放射源搜寻作业可能会探测不同能量或能量未知的γ射线，图2显示探测器响应是能量敏感的，通常需根据装置结构寻找合适的与能量弱相关的参数R，以实现角度分辨中对不同射线能量的普适性。此外，角度的分辨性能是定向装置功能的重要指标，需通过合理的结构设计达到最优的角度分辨能力。

1.1 能量关联性

根据γ射线斜射屏蔽材料的减弱规律φ(θ)=B(θ)φ0e-μtsec θ(φ0为无屏蔽下测点的辐射通量密度，B为累计因子，线吸收系数μ与射线能量E相关，而等效厚度t可看作是与角度θ相关的形状因子)，各探测器的响应函数可记为Hi(E,θ)(i=1,2,3,4)。图3为L=7 cm时射线的R与θ的关系。经比较发现对于0.3～1.3 MeV范围几个典型能量γ射线，以下关系式构造的R随θ变化规律基本重合，如图3b所示。

(1)

(2)

由于低能射线基本无法穿透铅屏蔽层厚度，可能造成背向辐射源的探测器计数接近0，导致R随角度变化规律与高能射线不尽相同，图3a所示为0.06、0.1、0.2 MeV 3种能量不同角度入射时的R分布。而对于大于1.3 MeV的更高能量的射线，其R随角度变化规律与图3b中1.3 MeV能量射线的曲线同样基本重合。显然R组合能近似表征此类铅屏蔽多GM计数器定向装置对γ射线的角度响应特点，尤其能回避因射线能量不同导致的响应差别。

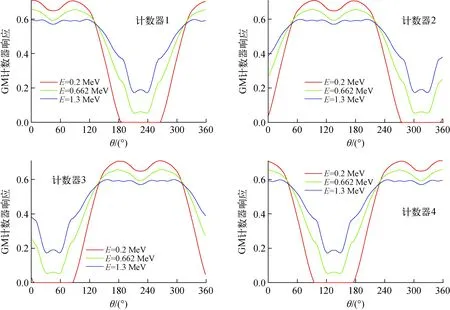
图2 归一化响应随角度变化规律Fig.2 Normalized response versus angle

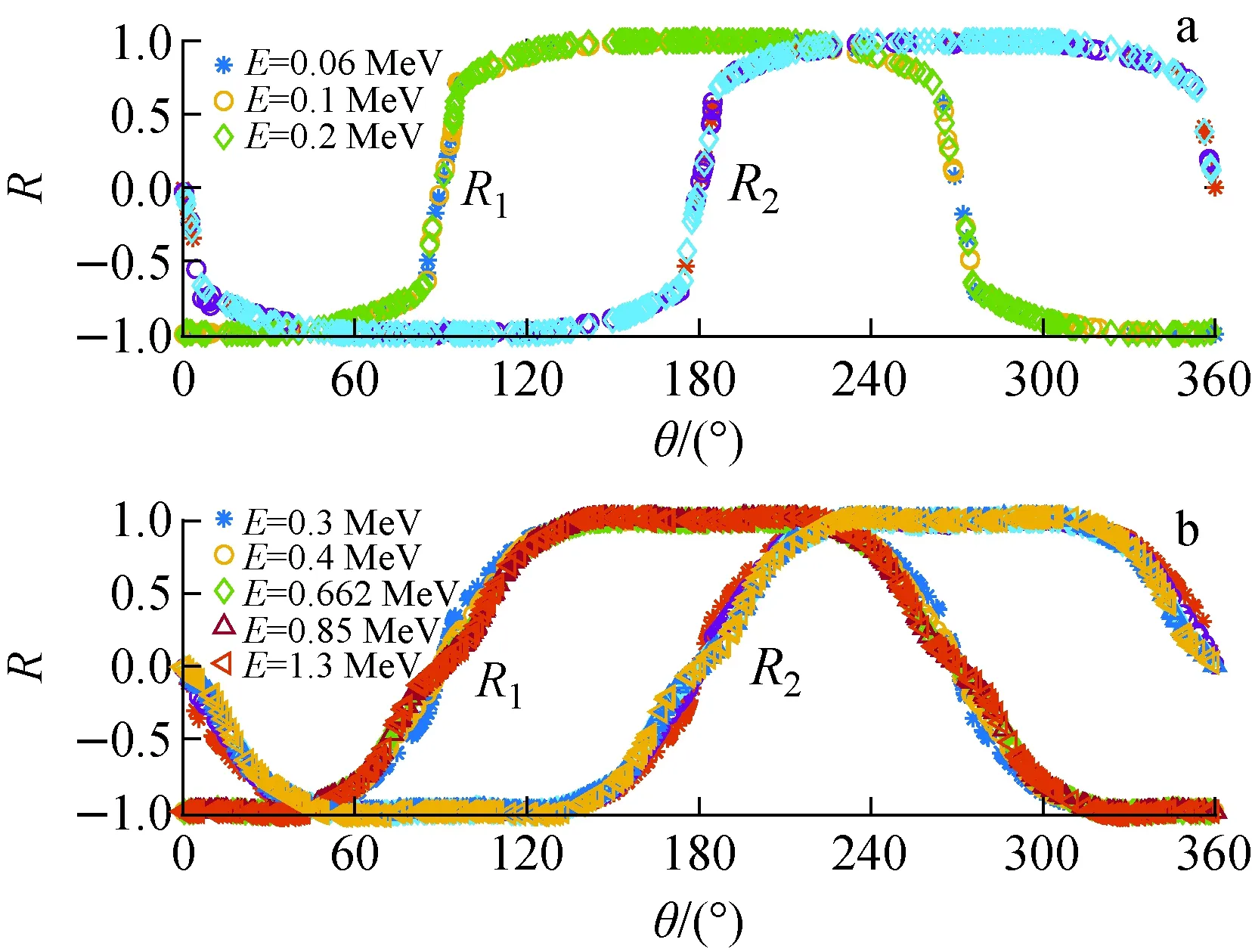
图3 多种能量射线R-θ关系Fig.3 R-θ relationship for different energy rays

1.2 结构关联性

在探测器位置和屏蔽层厚度一定的情况下，屏蔽体径向宽度L会显著影响探测器响应规律，图4显示了该装置在屏蔽体径向宽度L=5、7.5、8.5、10 cm且E=0.662 MeV下R组合与放射源入射角度的对应关系：L=5 cm时R1和R2在部分角度区间会同时出现连续平台；L=10 cm时在0°、90°、180°以及270°附近象限切换边界，R1和R2也会同时出现小段平台。角度分辨依赖于Hi组合和射线入射角度的隐含关系，而其R1-R2构造参数可看作表征角度变化规律的一种显性关系，因此可推测R1和R2同时存在平台可能不利于角度分辨的均匀性和可靠性；比较二者组合变化的可区分性，最终设置屏蔽体径向宽度L=7 cm。

2 角度反演算法比较

BP神经网络具有复杂模式分类能力和优良的多维函数映射能力，通过对训练样本输入-输出映射关系的学习反馈，不断调整节点连接权值而优化其网络模型，实现在给定输入值时得到最接近期望输出值的结果。本文主要采用该算法实现从响应矩阵到角度的反演。

利用GEANT4程序建立多探头组件定向装置模型，模拟计算定向测量探头对γ辐射的能量、角度响应特性，建立了能量分别为0.058、0.06、0.1、0.2、0.3、0.4、0.662、0.85、1.261、1.3、2.561、3 MeV的单能射线不同角度入射的剂量响应矩阵。对上述能量射线的响应样本，选择0.058、0.662和1.261 MeV的响应矩阵为验证样本用于检验算法效果，其他为训练样本用于建立神经网络模型。

算法的性能表现是BP神经网络算法建立过程中进行调试和选择的依据：对于模拟获得的理论计算样本，判断角度识别精度以及对射线能量依赖性即可比较算法优劣。但对于装置实际使用情形，则可能存在辐射本底、电子学噪声、信号失真等计数涨落的影响；此外GM计数器计数率通过刻度拟合计算剂量率时也存在误差，而且在不同剂量率点的误差分布不一致，导致在角度反演中存在误差剂量率效应，即同次测量中，该装置4个GM计数器因屏蔽结构而处于不同剂量率场，进而因测得的4个剂量率误差分布不一致导致角度反演误差增大。初步通过对探测器响应引入随机涨落来模拟计数扰动导致的误差，代入建立的神经网络模型中反演计算扰动计数下的角度并和未引入扰动时的结果进行比较，可测试算法对计数涨落的容忍度并评估其应用时的可靠性。

神经网络算法的性能与其网络结构、训练样本输入输出量选取等密切相关。网络结构设计通常需根据实际问题和经验进行选择取舍，利用MATLAB神经网络工具箱建立适合该问题的网络结构，并调试设置合适的隐藏层节点数、激活函数、训练函数、初始权值阈值等参数。测试发现相比于算法结构参数，本问题中影响算法性能的更主要因素是输入输出量的选取，对于上述响应矩阵建立的训练样本，输入输出量有图5所示的几种不同选取方式，其中角度区间二值化向量是将2π范围的角度按指定分辨精度θ0分段，每个角度区间[k,k+1]θ0以二值化向量[0,0,…,1,…,0,0]表示(第k个元素为1，其余为0)。因此对以下3种算法模型开展了讨论和比较。

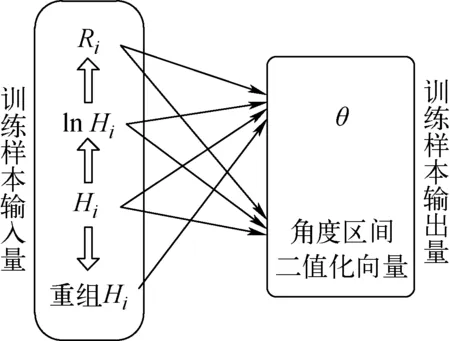
图5 不同训练样本模型Fig.5 Different models of training sample

2.1 以Hi为输入量

不同能量γ射线的Hi-θ具有不同的映射规律，模拟计算涵盖了0.058～3 MeV能量范围以使训练样本具有全局覆盖性。以Hi为输入量、θ为输出量对训练样本直接进行神经网络训练和学习，计算收敛后该网络模型的角度分辨能力如图6所示，大部分范围内反演精度在5°以内，180°和360°附近分辨能力相对较差；利用该神经网络对未经训练的验证样本进行测试，其计算角度偏差结果与图6类似；对Hi附加随机涨落后利用该神经网络进行角度计算的结果如图7所示，显示整体角度预测偏差较大，尤其在180°和360°(360°即0°)附近计算结果已不可信。

图6 Hi-θ神经网络训练结果Fig.6 Neural network training result of Hi-θ

图7 Hi-θ加涨落后神经网络预测结果Fig.7 Neural network training result of Hi-θ with fluctuation

2.2 以Ri为输入量

Ri是Hi经数学处理构造产生的1组用于回避角度反演时能量依赖性的参数，以Ri为输入量、θ为输出量，对训练样本进行神经网络训练学习的结果如图8a所示，角度反演精度约为±10°且呈现周期性变化；而同样对Hi引入随机涨落计算其相应的Ri，利用该网络计算的角度结果如图8b所示，可见偏差更大已完全失真。该方法偏差较大的原因在于由Hi4个参数构造为Ri两个参数，丢失了部分响应信息，此外还可能因为该构造参数在高能和低能的变化规律差别明显。

对输出量θ进行二值化，预先设置了一分辨范围，可对该计算模型进行改进。以Ri为输入量、角度区间的二值化向量作为输出量进行神经网络训练，如以θ0=5°分段，获得的训练结果如图9a所示，该方法在计算引入涨落的剂量时能适当控制角度预测结果的偏差，如图9b所示，其效果优于图7和图8b。

2.3 样本映射重组

由于探测装置理论上完全对称，为降低Hi-θ对应关系组成的样本集合因模拟计算可能出现的误差周期性不一致，可将[π/2,2π]范围的结果组合全部映射到[0,π/2]，然后以π/4角度轴再次镜像以扩大训练样本，该操作增强了角度识别的对称性，且理论上相当于将初始样本扩展了8倍。对重建后的样本以Hi为输入量、θ∈[0,π/2]为输出量进行神经网络训练和学习。利用该已训练的网络计算角度时需进行映射的逆操作，通过向量法确定射线入射角度的象限即可完成逆映射。样本映射重组法的神经网络训练结果如图10所示，不考虑数据涨落影响，理论上能将偏差控制在±1.5°以内；对Hi附加随机涨落后利用该神经网络进行角度计算的结果如图11所示，大部分角度偏差在±10°以内。可见该方法相比于前两种性能最好，原因在于一方面样本量的扩大提高了神经网络拟合精度，另一方面结合向量法能预先将角度计算限定于4个象限之一，压缩了误差空间。

图8 Ri-θ神经网络训练偏差及加涨落后预测结果Fig.8 Neural network training result of Ri-θ and its error with fluctuation

图9 Ri-θ(二值化)神经网络训练结果及加涨落后预测结果Fig.9 Neural network training result of Ri-binary θ and its error with fluctuation

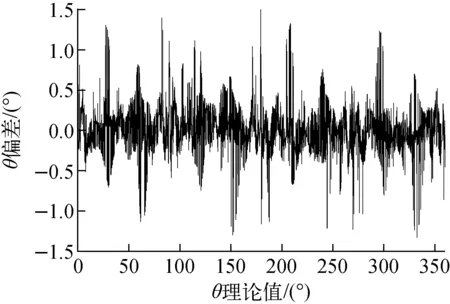
图10 重组Hi神经网络训练结果Fig.10 Neural network training result of reconstructed Hi

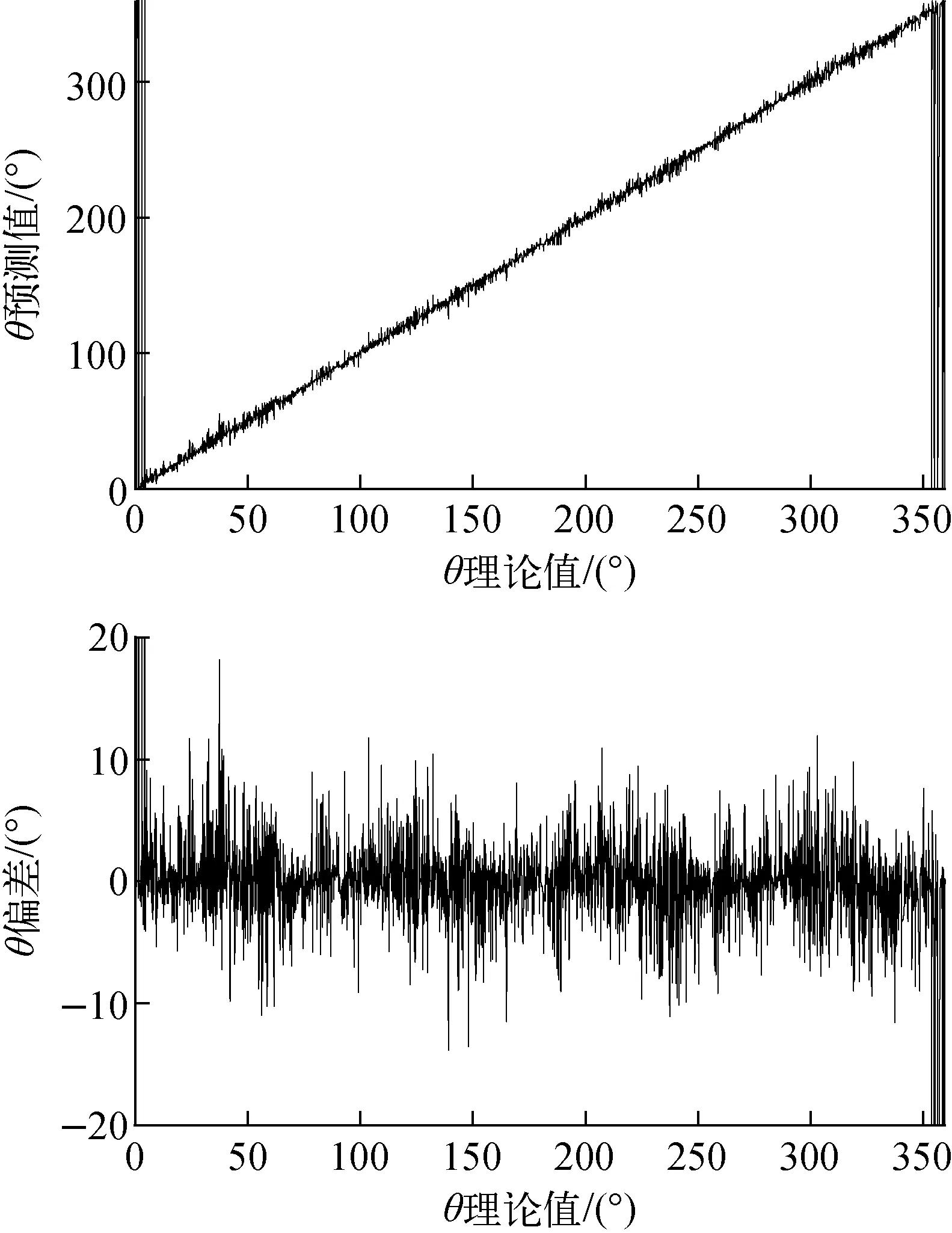
图11 重组Hi神经网络对加涨落数据的预测结果Fig.11 Neural network training result of reconstructed Hi with fluctuation

3 样机测试

GM计数器探测器经标准辐射场剂量率校准后，根据理论模型装配了辐射源定向装置样机，采用STM32单片机完成数据采集和角度反演算法功能。利用137Cs源开展角度探测的验证实验。将完整定向测量装置置于角度电动圆盘中心，并使测量装置与137Cs源等高，电动圆盘以遥控方式每次旋转固定间隔角度(本次实验选择11.25°)，记录射线不同入射角度时的GM计数器响应及上述算法给出的计算角度。对于[0,2π]范围的角度理论值，放射源角度实验测量值与神经网络模型模拟预测值的比较如图12a所示，装置实测值与实际角度值的偏差如图12b所示，在±6.25°以内。

误差整体表现为：在kπ/4(k为0～8的整数)的特征角度测量偏差最小，在1°以内；其他角度误差逐步增大，近似周期性。推测误差的变化规律可能与误差剂量率效应有关，误差最小的角度入射的射线恰好处于装置对称线上，剂量率误差也对称，因而整体角度反演误差小；而其他角度因为非对称性，剂量率误差分布不一致，因而角度反演误差增大。误差变化规律说明该装置计数率一致性相对较好，影响角度分辨精度的主要因素是剂量率误差分布的不一致程度。因此改进剂量率刻度拟合算法将有助于进一步提高装置角度分辨能力。此外误差还部分来源于装置实际尺寸与算法建模尺寸的偏差，也可能体现为对称方向误差相互抵消而变小。

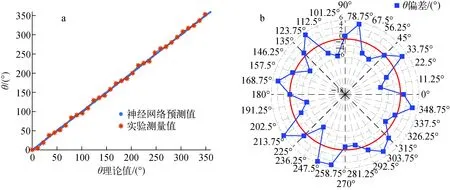
图12 定向装置137Cs源角度探测实验结果Fig.12 Experiment result of direction finder to 137Cs

4 结论

本文对基于十字铅屏蔽GM计数器组件设计的便携辐射源定向装置角度反演算法进行了讨论，理论上可通过角度识别精度以及对射线能量依赖性评价算法优劣，考虑实际GM计数器探测时的计数和剂量率换算误差，可通过引入随机涨落对算法进行测试。

1) 采用BP神经网络算法对蒙特卡罗程序模拟计算的样本进行训练学习，能实现对不同能量射线相同的角度识别能力，无需依赖于寻找与能量不相关的构造函数进行拟合；神经网络算法的训练样本输入输出模型对角度分辨精度和扰动容忍度有主要影响。

2) 构造的R可用于选择合适的铅屏蔽体径向宽度以提高角度分辨能力，用于角度反演算法时需区分射线的高低能量，且会因为信息减少而增大角度偏差；R到二值化角度的输入输出训练模型预先设置了角度分辨区间，在存在涨落时能改进角度反演计算结果，但总体效果差于映射重组法。

3) 直接训练法由于样本的独立同分布性不足，在周期边界处耦合能力差，而基于对称性对样本进行映射重组，理论上相当于将初始样本扩展了8倍，能实现±1.5°以内的角度分辨能力，在计数响应引入涨落的情况下也能实现约±10°以内的角度偏差。

样机在137Cs源辐射场进行了初步的角度识别验证实验，实测结果的角度偏差在±6.25°以内，对于装置对称位置的射线，角度偏差相对最小，符合理论预期，改进剂量率刻度拟合算法将有助于进一步提高装置角度分辨能力。