全液压动臂塔机变幅机构机液一体化仿真研究
2020-05-07赵玉香
费 烨, 赵玉香, 刘 海
(沈阳建筑大学 机械工程学院, 辽宁 沈阳 110168)
0 引言
塔式起重机是高层或超高层建筑施工中的主要施工机械, 它通过改变起重臂仰角实现变幅以满足不同工况需求。全液压动臂塔机动臂自重大且带载变幅,变幅过程产生惯性载荷影响结构疲劳强度, 还会对液压系统造成冲击。因此,对大型全液压动臂塔机变幅的动态特性进行研究十分必要。
为此, 崔少杰等借助有限元法对动臂塔机变幅过程中的模态变化进行分析, 结果表明动臂仰角变化对整机固有频率影响较大[1];付玲等利用多体动力学方法对动臂塔机变幅过程突然卸载工况进行仿真分析, 发现突然卸载时臂架内弹性势能释放导致臂架振动对其结构强度有明显影响[2];文献[3,4]则对动臂塔机变幅卸载防后倾进行了研究。 上述研究从对象看,均关注于动臂塔机变幅突然卸载对塔机的影响, 其实动臂变幅起吊载荷瞬间臂架内弹性势能也会变化导致动态过程。 从研究方法看,现有研究单一的从动臂塔机的结构、机构角度建模分析,忽略了变幅机构液压驱动系统的耦合性影响。
本文综合考虑动臂塔机变幅过程中机、 液间的耦合作用,借助塔机变幅系统的机液一体化仿真技术[5-7],建立全液压动臂塔机变幅机构模型, 通过联合仿真分析全液压动臂塔机变幅启动负载时机、液系统的动态特性。
1 液压动臂塔变幅机构机液一体化模型建立
1.1 变幅机构仿真模型的搭建
依据某型全液压动臂塔机实际结构,借助Solidworks完成其变幅机构三维模型的建立。主要由平衡臂、塔头和臂架组成。 平衡臂与塔头和臂架直接相连, 塔头由前撑架、后支架和变幅定滑轮座三部分组成。前撑架和定滑轮座通过螺栓固接,后支架和定滑轮座通过销轴连接。完成的变幅机构三维模型如图1 所示。
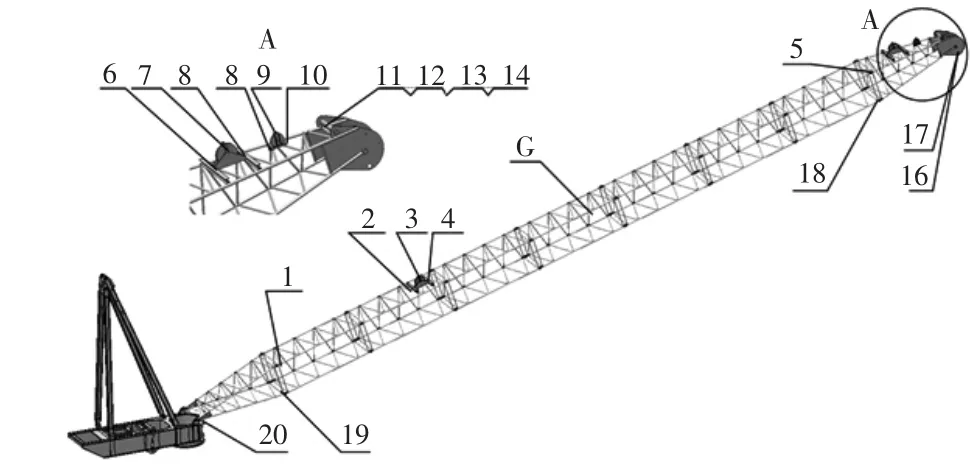
图1 变幅机构三维模型
变幅机构仿真模型由动臂、塔头、变幅卷筒和变幅滑轮组、起升卷筒和起升滑轮组组成。其动臂的初始仰角为17°,根据动臂的结构和受力点选取了20 个坐标点,其中序号3,7,10,16 是起升滑轮组定滑轮连接点,序号17 是起升钢丝绳绕过动滑轮固定端连接点,序号13 是连接变幅动滑轮组的拉绳连接点。 根据工程图建立平面直角坐标系, 以动臂和平衡臂的连接点作为原点, 测量各点坐标,根据三维模型确定动臂重心坐标,作为动臂平面机械库模型的参数[8,9];为了简化塔头建模将其视为整体,坐标选取和测量过程与动臂类似; 变幅滑轮组和起升滑轮组在平面机械库中选取定滑轮和动滑轮元件, 根据缠绕方式搭建出变幅滑轮组和起升滑轮组的仿真模型。 变幅滑轮组一端与定滑轮座相连, 另一端通过四根钢丝绳与动臂头部相连。 完成变幅机构模型如图2 所示。
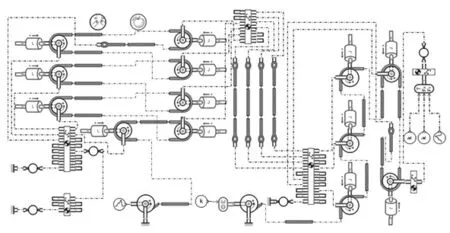
图2 变幅机构仿真模型
1.2 变幅机构液压驱动回路模型的搭建
全液压动臂塔机由液压回路驱动变幅, 其工作原理如图3 所示。变幅时,液压泵输出压力油经换向阀到变幅马达左右两腔,实现其正反转。马达产生转矩经减速机传递给变幅卷筒带动钢丝绳通过滑轮组缠绕或放出, 牵引动臂俯仰改变塔机工作幅度。
依据回路组成, 利用AMESim 搭建出变幅回路模型如图4 所示。

图3 变幅液压系统原理图
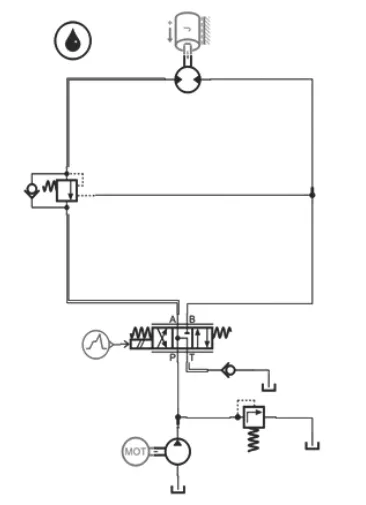
图4 变幅机构液压驱动回路仿真模型
1.3 变幅机构机液一体化仿真模型
将变幅机构模型通过减速机与液压回路模型相连,得到变幅机构机液一体化仿真模型如图5 所示。
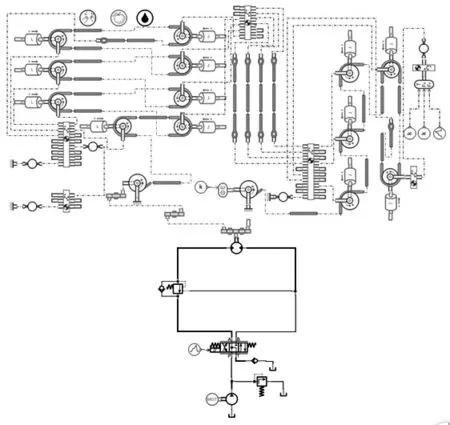
图5 变幅机构机液一体化仿真模型
2 变幅机构机液一体化模型验证
2.1 仿真工况设定
该塔机动臂仰角在17°~80°变化,考虑到样本实测数据,本文以空载往复变幅过程对该模型进行验证。主要参数见表1。
2.2 仿真结果
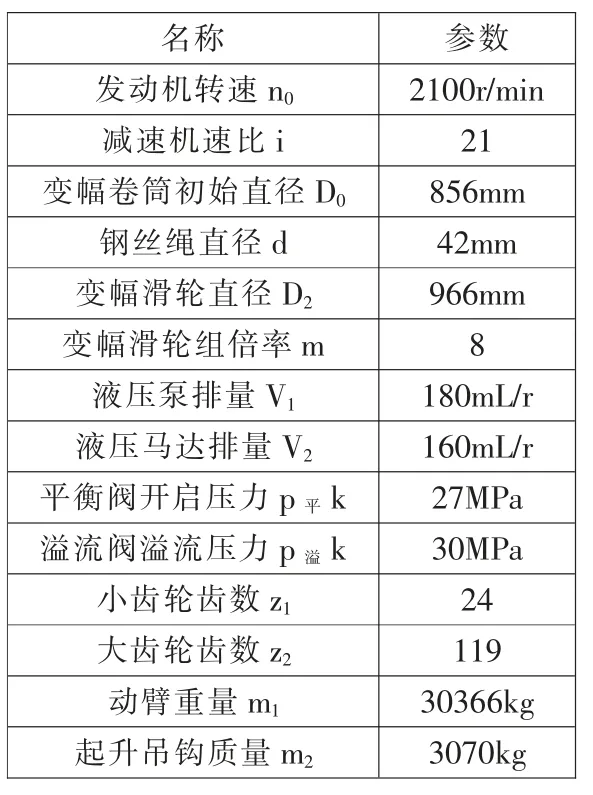
表1 变幅系统主要参数
将表1 中的数据,输入到仿真模型,运行仿真, 得动臂仰角变化曲线、 变幅马达双腔压差和钢丝绳拉力曲线如图6~8。
塔机实验测得,动臂空载从17°变幅到80°时间130 s。 从80°变幅到17°时间120 s。 图6 仿真所得时 间 为129 s、122 s,最大误差误差1.7%。
由图7 知,变幅起升4s 马达压差开始稳定,此时动臂仰角18°,马达压差23.02MPa。 随着动臂仰角增大,负载扭矩减小,马达压差随之减小。 74s 时变幅卷筒钢丝绳缠绕层数增加,马达压差随之阶跃增大。 74~130s 变幅卷筒直径不再发生变化压差呈递减趋势变化; 之后悬停制动,马达压差在5.81MPa 波动,此时动臂仰角80°。 140~262s 动臂回落,平衡阀未开导致马达进油腔压力升高,进油路压力增至平衡阀控制压力时, 马达回油经平衡阀流回油箱,而后马达压差呈递增趋势变化。197s 马达压差因变幅卷筒直径减小突然下降。 之后动臂下降18°时,马达两腔压差22.6MPa。
图8 表明, 动臂刚启动时钢丝绳拉力最大且剧烈波动, 经4s 趋于稳定, 此时动臂仰角18°, 钢丝绳拉力237016.6N; 动臂仰角80°时钢丝绳拉力最小其值为52458.06N。 动臂下降至18°时,钢丝绳拉力236996.6N。
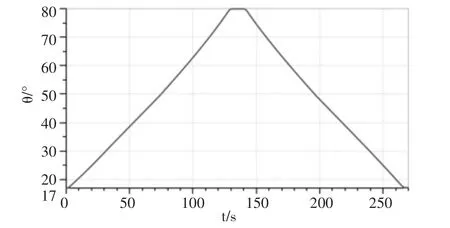
图6 动臂仰角变化曲线
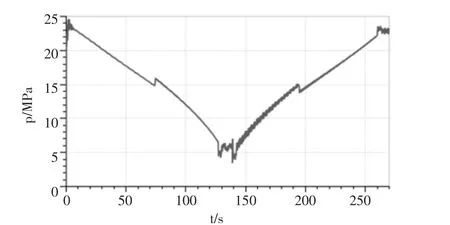
图7 马达压差曲线
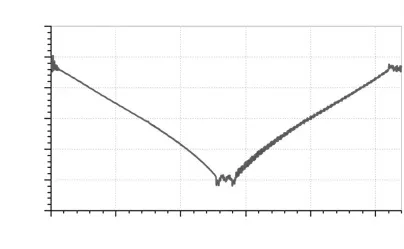
图8 钢丝绳拉力
2.3 理论计算
对塔机空载动臂仰角为18°、80°时进行受力分析如图9 所示。
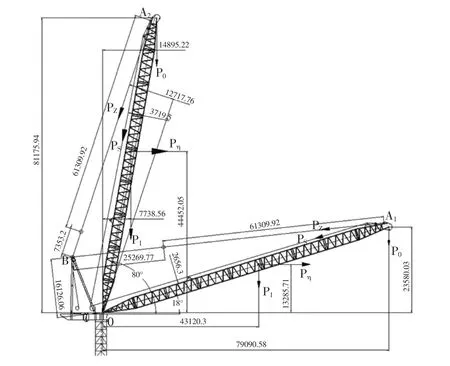
图9 动臂受力分析图
对O 点取矩并令∑MO=0,求得动臂两仰角钢丝绳拉力[10]:
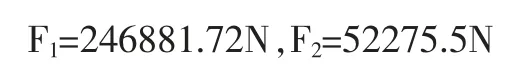
变幅马达输出扭矩及马达两腔压差公式为:

式中:F—动臂单根钢丝绳拉力;n—变幅卷筒钢丝绳层数;ηm—马达机械效率0.95;其他符号见表1。
该塔机动臂仰角18°时, 变幅卷筒缠绕两层钢丝绳,即n=2;动臂仰角80°时,n=3。
将表1 数据代入公式(1)、(2)可求得:
动臂仰角为18°时:
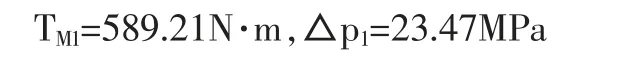
动臂仰角为80°时:
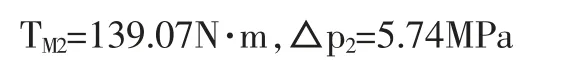
上述计算表明,动臂仰角18°时,马达压差最大误差3.71%、钢丝绳拉力最大误差4%;动臂仰角80°时马达压差误差为1.22%、钢丝绳拉力误差为0.34%。 均在误差允许范围内, 且曲线趋势正确。 说明该机液一体化模型正确,可以模拟仿真带载变幅过程。
3 变幅机构动态特性仿真分析及改进
3.1 最大工作幅度下变幅过程仿真
该型塔机最大起重量100t, 最大起重力矩2400t·m。按照其起重特性, 以最大工作幅度80m 时起重13t 工况对变幅过程的动态过程进行仿真。
马达压差如图10 所示, 马达压差在3s 内剧烈波动后趋于稳定。
钢丝绳拉力如图11 所示,随着动臂仰角增加拉力逐渐减小,动臂刚起升时,3 s 内钢丝绳拉力波动剧烈,动臂振动,动臂与钢丝绳连接处的位移变化如图12 所示。
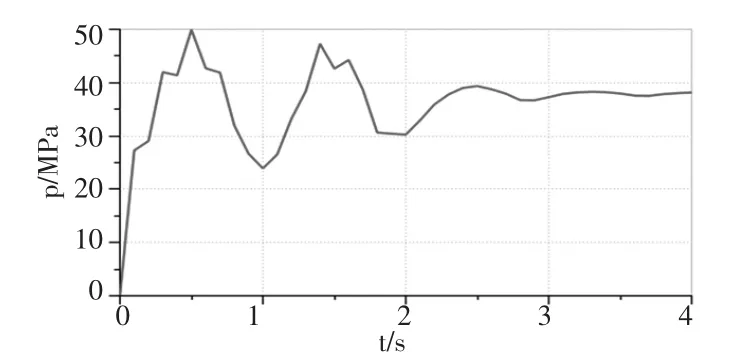
图10 马达压差曲线
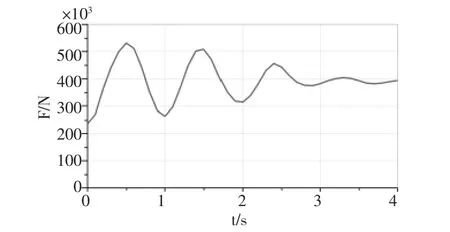
图11 钢丝绳拉力
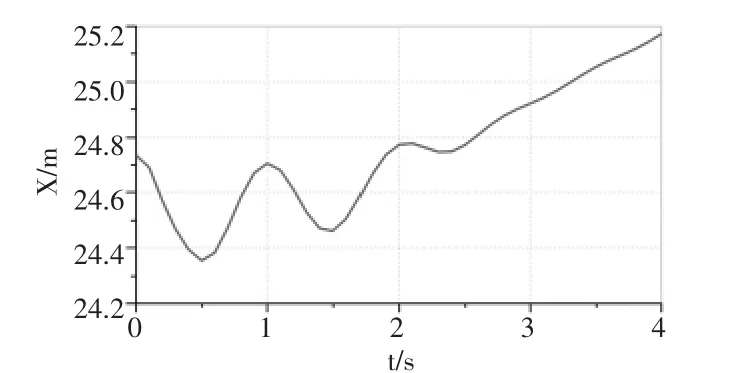
图12 动臂头部位移
可见,动臂变幅启动时产生较大的惯性载荷,导致振动和压力冲击,液压系统出现压力冲击。究其原因是在工况转变过程中, 塔机变幅机构带载变幅时会产生大的惯性载荷所致,继而导致液压系统压力冲击,又反作用于塔机动臂。 显然这会影响液压元件的使用寿命和工作的平稳性[11,12],需对液压系统进行改进。
3.2 变幅机构液压系统改进
仿真实验表明, 平衡阀和溢流阀开启压力对动臂变幅平稳性有重要影响, 通过对图5 模型的批处理仿真实验, 设置平衡阀开启压力28.4MPa、 溢流阀开启压力36.8MPa 变幅过程更为平稳,仿真结果如图13~15 所示。
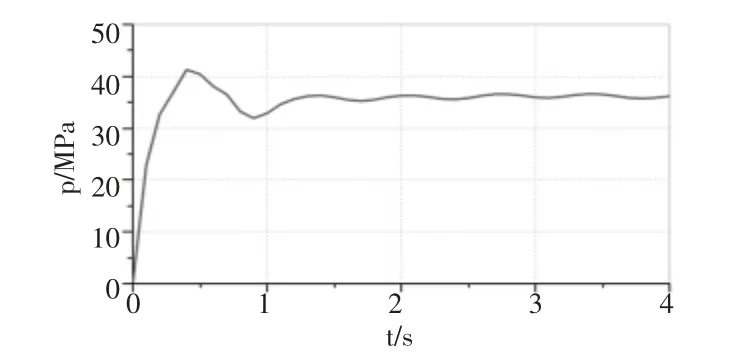
图13 马达压差
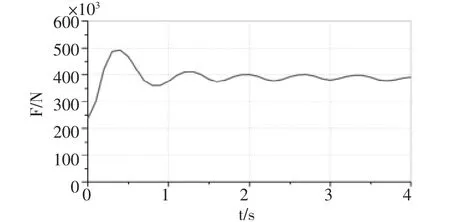
图14 钢丝绳拉力
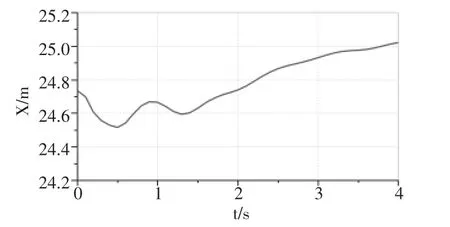
图15 动臂头部位移
改进后的液压塔机变幅系统, 马达压力冲击峰值下降17.4%,钢丝绳拉力峰值下降7.6%,动臂振动的最大振幅减小了40.1%。 因此,变幅性能更好。
4 结论
基于AMESim 软件建立了国产某型全液压动臂塔机变幅机构机液一体化仿真模型, 据此对变幅过程进行了仿真研究,结果表明:
(1)动臂变幅启动过程会导致动臂振动和变幅回路的压力冲击。
(2)变幅回路中平衡阀和溢流阀开启压力对动臂塔机变幅平稳性有重要影响, 就所研究机型而言合理设置该参数可使动臂启动变幅时的最大振幅减小40.1%, 回路压力冲击峰值下降17.4%。
上述结论对全液压动臂塔机改进设计具有借鉴意义。
