压水堆核电厂安注管线内不凝结性气体聚集现象仿真研究
2020-05-07朱光昱全峰阳元一单
朱光昱,全峰阳,曾 骁,元一单
(中国核电工程有限公司 核电安全研究中心,北京 100840)
核电厂中死管段现象通常发生在与一回路相连且处于隔离状态的管道中,该现象会导致气体在管道内聚集,使水中的有害杂质浓缩,加速管道内的化学腐蚀过程,提高核电厂的维修成本[1-3]。一般认为死管段现象发生的原因是管道中的水被加热汽化或管段内的压力不能维持高于水的饱和压力[1],即死管段中的气体聚集现象是由水汽化产生的。
长期处于冷态备用的系统应主要关注不凝结性气体导致的死管段现象。在西屋公司标准运行技术规格书[4]中,对避免不凝结性气体聚集导致死管段现象规定了必要的措施。例如,在运行限制条件3.5.2(NUREG-1431 STS Rev.4.0 LCO 3.5.2)的依据[5]中说明,核电厂正常运行工况下,安全注入系统长期处于备用状态,因此,流经管道内可能积累不凝结性气体(空气、氢气、氮气)形成死管段,这将导致安全信号启动后发生水锤、泵气蚀等影响系统功能的现象,甚至不凝结性气体可能注入一回路中。为了避免上述问题发生,在运行限制条件监督要求3.5.2.3中规定,运行人员需每31d核实安注管线的满水状态。根据运行经验,该监督要求可通过对安注管线执行排气操作来实现。
一般情况下,气体在水中的溶解度仅与温度和压力相关[6],在安全注入系统投运之前,管线内的压力几乎不变,因此可以认为,管线内的不凝结性气体析出仅是由温度波动导致的。基于上述假设,本文采用数值模拟手段对压水堆核电厂安注管线内不凝结性气体聚集现象进行了仿真研究,初步探讨西屋公司标准运行技术规格书中规定的每31d核实安注管线满水状态的监督频度设置依据。
1 计算模型
COMSOL计算平台是采用有限元方法的仿真模拟软件,具有多种内置计算模型,适用于多物理场耦合仿真研究。本文采用气泡流-层流模型耦合流体传热模型,对温度波动导致的不凝结性气体析出现象进行研究。气泡流-层流模型[7]常用于模拟分散气泡驱动流体的低雷诺数和中等雷诺数流动,适用于气相含量较小的工况。该模型只求解一组液相的纳维-斯托克斯方程,同时使用滑移模型来调整气泡速度。液相的动量方程如式(1)[8]所示。模型中的压力分布通过式(2)[8]混合物的平均连续性方程来计算,并通过求解有效气体密度的输运方程跟踪气相的体积分数。
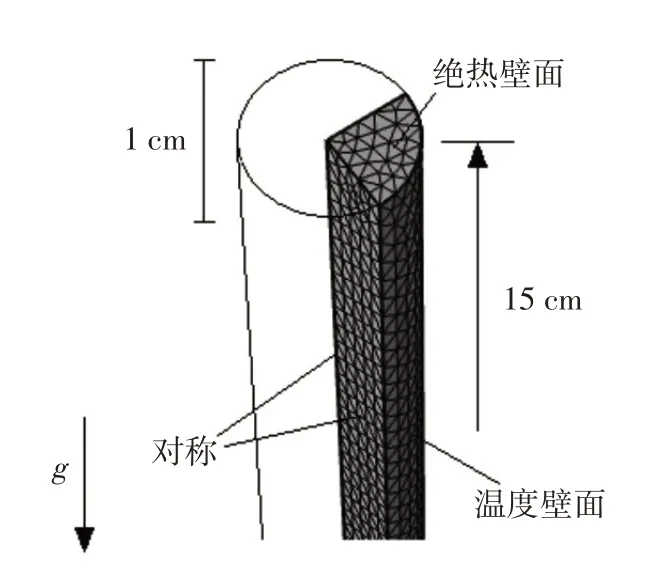
图1 计算域和网格划分Fig.1 Calculation domain and mesh generation
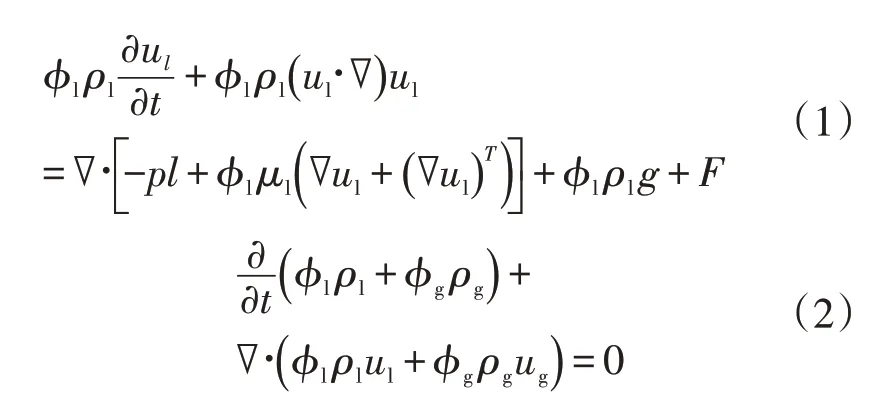
式中,Φ——体积分数;
ρ——密度,kg/m3;
u——速度,m/s;
μ——黏度,Pa·s;
T——热力学温度,K;
g——重力加速度,m/s2;
P——压力,N;
F——液相受到的体积力,N。
模拟工质采用水和空气,在气泡流模型中空气密度采用式(3)计算,同时考虑了温度对水物性的影响,相关参数设置见表1。
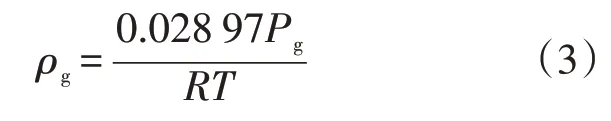
式中,Pg——气相压力,N;
R——气体常数。

表1 水的物性参数设置Table 1 The related parameters of water
对于气体析出的过程,本文在模型设置中还需要开启低气体浓度修正和求解相界面面积两个选项。计算采用的滑移模型为压差阻力平衡,曳力系数设置为球状小气泡,气泡直径设置为1 mm。由于安注系统管线均位于厂房内部,因此,本次模拟仅考虑管壁温度在室温范围内的变化,此时每立方米水中溶解的空气质量与温度近似呈线性关系,可采用式(4)计算。

由于核电厂房内的温度波动相对缓慢,因此,本次模拟可以忽略空气在水中溶解和析出的物理过程需要的时间。本文通过在计算域内添加质量传递输运方程来模拟温度波动导致的空气在水中的溶解或析出过程,其瞬态方程如式(5)[10]所示。
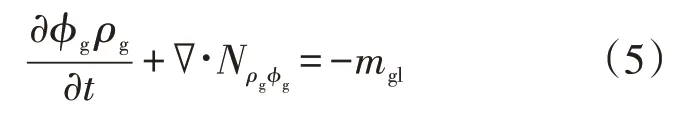
式中,N——浓度;
mgl——气相到液相的质量传递速率,kg∕(m3·s)。
在初始化阶段,假设水中的空气已经处于最大溶解度状态,因此,水温升高将导致液相向气相传质,同理,水温降低将导致气相向液相传质。由于水的密度远大于空气密度,该传质过程对水质量的影响可以忽略不计。
本次模拟工作仅对不凝结性气体析出规律进行研究,不对整体安注管线内的实际气体聚集情况进行仿真,因此采用直径为1 cm,管道长度为15 cm 的竖直短管作为计算模型。如图1所示,由于管道内物理场是对称的,为减少计算量,本文最终采用的计算域为管道的1∕4。管道两端和管道外壁面均设置为无滑移的壁面,为了研究温度对气体溶解度的影响,管道外壁面还设置了温度边界条件。由于管道内的水近似静止状态,因此,可以忽略流体动力学的影响,采用COMSOL 预定义的普通物理对网格进行校准,最终采用的划分等级为极细化,计算域网格数为17 141。
2 模拟结果
图2为温度在12 h内由17.5 ℃升高至22.5 ℃过程的模拟结果。随着温度升高,水中溶解的空气逐渐析出,析出的空气会在浮力作用下聚集在管道顶部。图中空气会聚集在靠近管壁的位置,这与一般的物理过程相符合,证明计算模型设置是比较合理的。
西屋公司标准运行技术规格书中规定的核实管道满水监督频度为31d,因此,本文需要研究长时间温度波动条件下管道内的空气聚集现象。气温的日间变化一般采用正弦曲线法[9],国际上通用的土壤温波方程也是采用正弦函数模拟[10],本文借鉴上述思路对厂房内的气温波动进行模拟。考虑到厂房内保温较好,因此,本文将管壁处的温度条件设置为以24 h 为周期的小幅度正弦变化。图3 分别为气温在2 ℃、3 ℃、4 ℃和5 ℃范围内波动时,720 h(30 d)内管道内气相体积分数的变化趋势。
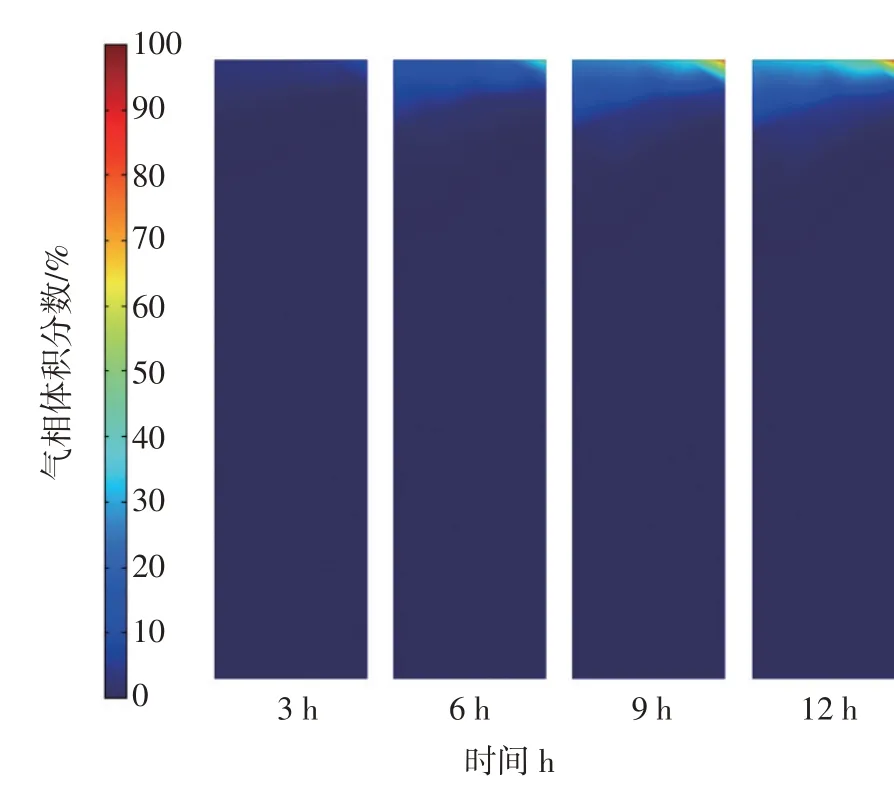
图2 管道顶部气相体积分数Fig.2 Air volume fraction of the pipe's top area
如图3所示,管道内始终会有一定量的空气无法重新溶解到水中,而由于浮力作用,这些气体会聚集在管道的顶端。发生该现象是因为升温时,管道内均发生气体析出现象,而当温度降低时,由于空气聚集在管道顶部区域,溶解的过程仅在发生顶部区域。约25d后,随着管道顶部聚集的空气增多,温度降低时空气溶解量逐渐增加,24 h内析出和溶解的空气量达到平衡,因此,管道内的整体气相体积分数的低点和高点几乎不再随着时间增加而改变。参考上述仿真结果,安注系统管线的排气操作应以不低于25 d∕次的频度执行,以避免排气效果不佳。
3 结论
本文采用COMSOL软件建立了长度为15 cm、直径为1 cm 的管道模型,对由温度波动导致的充水管道内的不凝结性气体聚集现象进行了仿真研究。仿真结果表明,安注系统管线满水的监督要求应以不低于25 d∕次的频度执行。在运行技术规格书中监督要求的设计过程中,监督频度会在满足验证需要的情况下,考虑人员操作的便利性,因此,仿真结果初步说明了西屋标准技术规格书中规定的每31 d 核实一次安注管线的满水状态的要求的合理性。
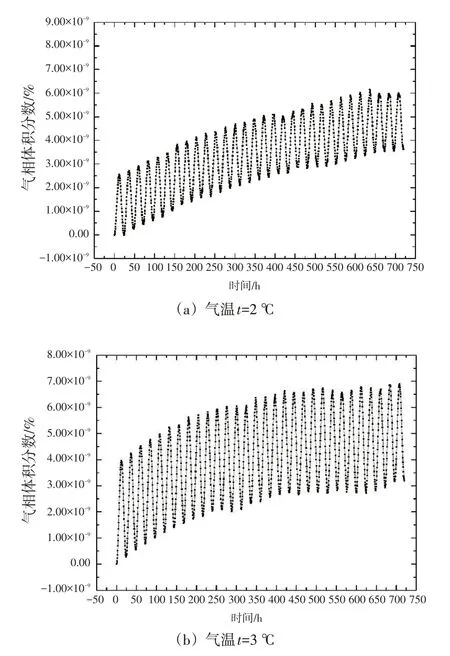
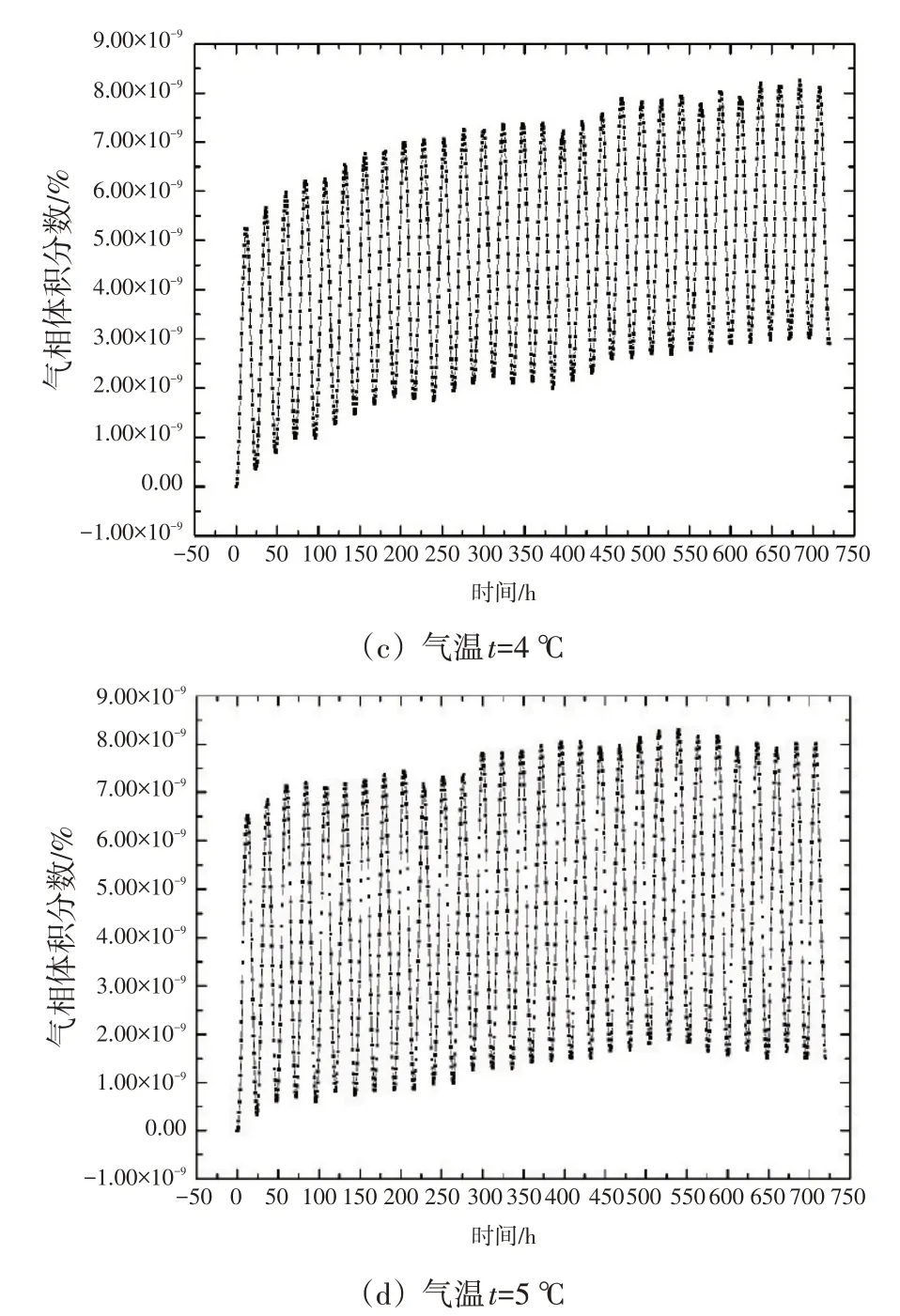
图3 气温在2 ℃、3 ℃、4 ℃和5 ℃范围内波动条件下,720 h内管道的气相体积分数Fig.3 Air volume fraction of the pipe with the temperature change in the range of 2 ℃、3 ℃、4 ℃and 5 ℃
