交替边界条件下多孔床传热传质特性数值模拟

宋潞云 张辉

东南大学能源与环境学院

0 引言

近年来，为了降低雾霾造成的危害，各种类型的新风机应运而生[1-3]。多数新风机在过滤PM2.5 颗粒物的同时，通常会采用全热交换芯进行排风的能量回收[4-5]。由于这些热交换芯的存在，会导致新风机中的阻力变大，通风能耗增加。如果采用基于多孔介质的回热式热交换方式，回热器在进风和排风通道中交替进行传热传质，可以在实现全热交换的同时，显著降低通风阻力，并可以通过改善结构设计实现新风机的微型化。本文针对回热式新风机中的多孔介质回热器在交替边界条件下的传热传质特性进行研究，为新风机设计提供依据。

目前对多孔床传热传质的研究主要集中在流道的结构形式[6-9]，多孔材料性能改进[10-13]和多孔床的运行控制及能效分析[14-17]等几个方面。且已有关于多孔介质传热传质的研究多为处理恒温、等热流边界条件的问题[17-19]，而对于在循环周期变化的边界条件下多孔介质内流动与传热问题的研究则相对较少[20-21]，循环交替边界条件是一类典型的非稳态边界条件，在一般的工程问题中均会遇到，是一种普遍存在的现象[22]。

本文以多孔材料为基本热湿交换媒介，考虑带有一定吸附能力的多孔介质在交替边界条件下传热传质特性，本文建立了空气主流区与多孔壁面区域耦合计算的数学模型，采用数值方法模拟了该多孔床传热传质特性，讨论了交替边界条件下多孔床内的传热传质规律。

1 传热传质模型

1.1 物理模型

本文所研究的计算区域物理模型如图1 所示：上层为自由流体区域，下层为多孔介质区域。上下层均受非渗透性固体壁面边界的限制。温度T1、含湿量为wa,1的空气以速度U1从左侧流过空气通道，半周期后，温度T2、含湿量为w a,2的空气以速度U2从右侧流过空气通道。在计算中假设多孔区域内每个局部的固体骨架和流体温度、含湿量相同。主流方向为X，垂直于主流方向为Y。

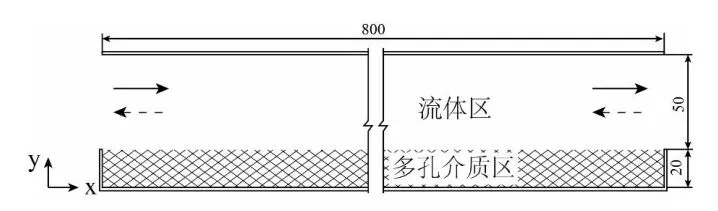
图1 物理模型

1.2 控制方程

本文对所研究的对象包括纯流体区和多孔区域，计算模型中作了如下假设：1）流道中的流体为不可压流体。2）多孔介质区域满足局部热平衡假设。3）忽略温度对物性的影响。4）多孔材料为均匀各项同性。5）忽略重力等体积力的影响。6）空气中其他气体在吸附剂中的吸附忽略不计。

1.2.1 流体区

在非多孔介质区域，二维流动与传热传质的控制方程为：

1）连续性方程

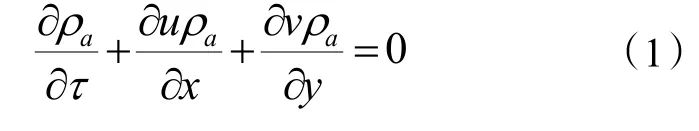
式中：ρa为气体密度，kg/m3；u、v为气体在x、y方向的分速度，m/s。

2）动量方程

式中：p为气体总压，Pa；μ为气体的动力粘度，N·s/m2。

3）能量方程

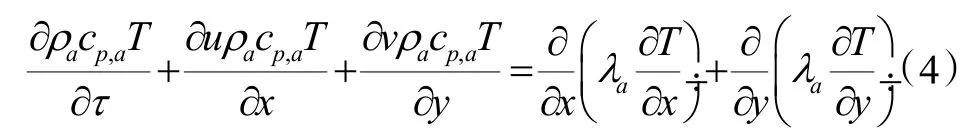
式中：T为温度，K；c p,a为空气比热容，J/(kg·K)；λa为空气的传热系数，W/(m·K)。

4）组分守恒方程

式中：wa为水蒸气的质量浓度，k g/m3；D为水蒸气在空气中的扩散系数，m2/s。

1.2.2 多孔介质区

在多孔介质区域，其二维传热传质的数学模型为：

1）连续性方程

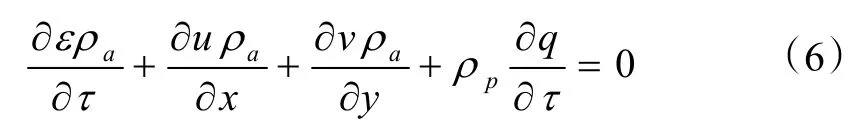
式中：ε为吸附床的孔隙率；q为吸附床的吸附质量百分比。

2）动量方程

式中：K为吸附床的渗透率惯性力常数C可使用Ergun 公式计算，C=1.75×(175ε3)-0.5。

3）能量方程

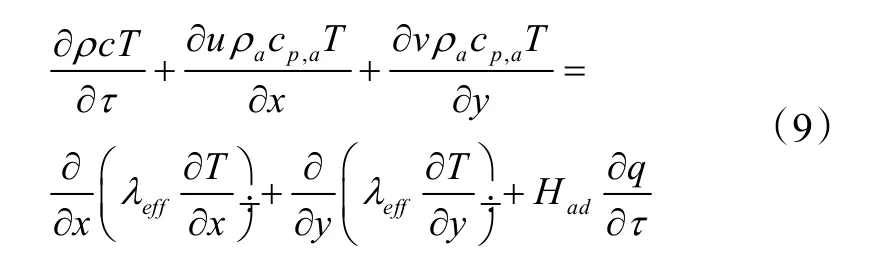
式中：λeff为床层有效传热系数，W/(m·K)；Had为吸附床多孔材料的吸附潜热，J/kg。

4）组分守恒方程

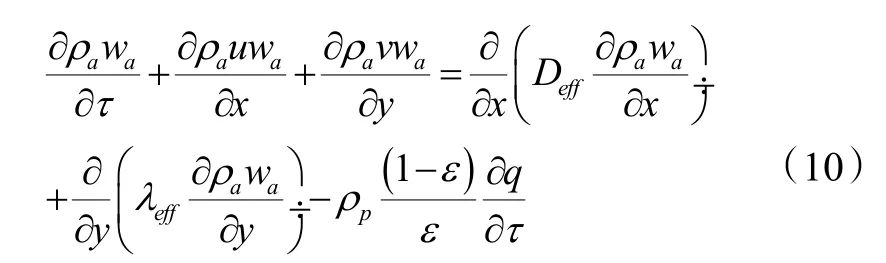
式中：Deff为床层内水蒸气的有效扩散系数，m2/s。

5）传质速率方程

水蒸气在吸附剂中的传质阻力主要来自气体在颗粒大孔内的扩散阻力，其传质速率可以采用线性推动力模型（LDF）描述。

式中：q*为组分的平衡吸附量，kg/kg；k为组分的传质驱动力系数，受瞬时流速、瞬时温度等因素的影响。

6）吸附平衡方程

传统的单组分吸附等温型方程包括 Langmuir 方程，Langmuir-Freudlich 方程，Dubinin-Astakhov(D-A)方程等，这些方程被广泛应用[25]。本文采用 Langmuir方程描述多孔床内水蒸气的吸附平衡过程。

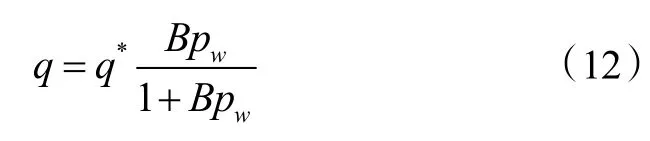
2 模拟条件和求解

2.1 边界条件及初始条件

流体区和多孔区的交界面满足温、湿度连续、热流连续、质量流连续的条件。多孔区壁面以及流体区顶面取绝热边界条件。在主流区入口处假设流体速度、温度含湿量分布均匀，出口采用充分发展条件。因此主流区的左右边界条件为：

1）前半周期，u＞0：在x=0处：T=T1；wa=wa,1；u=u1；在x=L处：∂T/∂x=∂wa/∂x=0

2）后半周期，u＜0：在x=0处：∂T/∂x=∂wa/∂x=0；在x=L处：T=T2；wa=wa,2；u=u2

计算区域内的初始压力为 101325 Pa，初始温度293 K，初始含湿量为零。

采用有限容积法对计算区域内控制方程进行离散，对流项选用幂函数格式进行离散。压力与速度的耦合采用SIMPLE 算法处理，离散后所得的代数方程组采用三对角矩阵法（TDMA））进行求解。为避免发散，迭代计算时采用欠松弛方法。同时模拟过程中考虑了数值模拟结果的网格独立性。

2.2 计算条件

模拟计算起始于多孔床放热吸湿的开始时刻。循环周期为 6 min，放热过程 3 min，吸热过程 3 min。模拟中采用的多孔介质为硅胶，平均颗粒直径 3 mm，孔隙率42%，初始温度为20 ℃，初始含水率为0。表1 列出了模拟中的操作条件。

表1 模拟的操作条件

3 结果与讨论

3.1 出口温湿度变化情况

图2 为当经过了几个周期循环处于稳定状态之后，多孔床出口处空气的平均温湿度与入口温湿度比值随时间变化情况。可以看到，切换开始时传热传质效果最好，并随着时间效果不断减弱。出口空气的温度在切换后很短时间内急速变化，迅速达到一个稳定值，而出口含湿量也在切换后1 min 的时间内达到一个稳定值。因为切换开始时床层与空气时间的温湿度差最大，传热速率较大，故传热效果最好。随着多孔床与空气间热量交换的进行，温度差变小，传热速率也变小，空气出入口温差逐渐降低并趋于稳定。而对于湿分的传递，可以看到后半周期只在切换后的短时间内与前半周期残留的气体有些许交换，使得出口空气含湿量提高，之后由于多孔床的吸附，空气出口含湿量下降，由于后半周期空气中的含湿量较低，质量交换量低于前半周期。

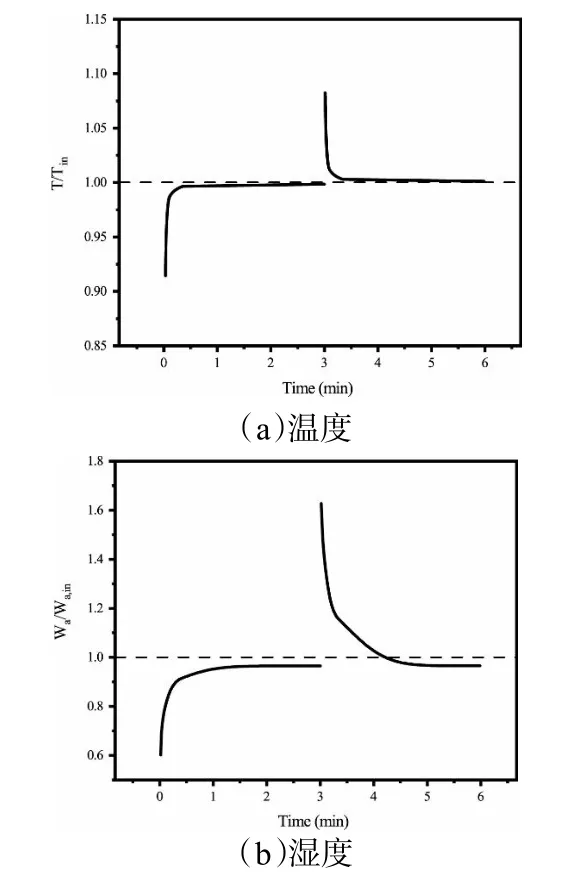
图2 出口处空气温、湿度随时间变化情况

3.2 多孔床内温、湿度分布

图3 所示为多孔床内节点在一个周期内温度变化情况。可以看出，靠近换热边界层的点其温度随时间变化较快，越靠近多孔床底层处各点温度随时间变化存在一定的滞后。多孔床内各点沿径向都具有一定的温度梯度，随着径向距离的增加，温度梯度逐渐减小，温度的变化幅度减小。

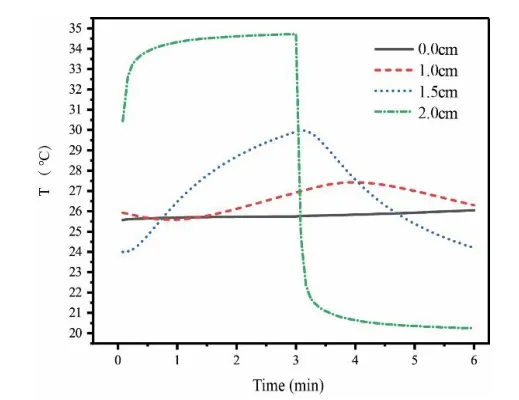
图3 多孔床内节点温度变化情况

图4 所示为x=0.5L处多孔床层在不同时刻的径向温度分布情况。可以看出，温度变化主要发生在多孔床和流体交界的表层，随着厚度的增加，多孔床的温度波动幅度逐渐减小。其主要原因是吸附剂的导热系数比较小，导热性能比较差。为了改善这一情况，强化多孔床传热，通常增加多孔床的有效传热面积，如可在多孔床中增加翅片。还可以强化多孔介质的导热系数，如对多孔介质进行改性处理或使多孔介质与导热性能好的材料固结在一起增大导热系数。

图4 x/L=0.5 处多孔床层不同时刻的径向温度分布

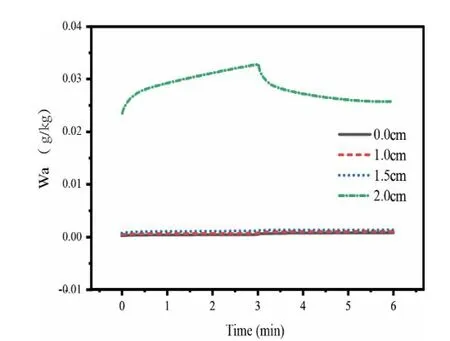
图5 多孔床内空气节点含湿量变化情况

图5 所示为多孔床内节点在一个周期内含湿量变化情况。可以看见，只有交界面附近较浅的表层节点有随着交替气流的呈现明显周期变化。靠底层的多孔介质含湿量在短时间内几乎没有变化。因此在使用多孔介质作为吸、解湿材料时，吸附层的厚度可以不用很大。

图6 所示为x=0.5L处多孔床层在不同时刻的径向含湿量分布。从图中可以看出，湿分的传播速度远低于热量的传播速度。由于多孔介质的吸附交界面附近的空气含湿量很低，且多孔介质的吸、解湿集中在很薄的浅表层，靠近多孔介质与流体交界面的湿度变化较明显，交界面附近的多孔材料吸收的湿分还未来得及向底层传递，湿分就多孔介质吸附或少量传递给了后半周期换向后的空气，而靠近多孔床底层的含湿量几乎不变。

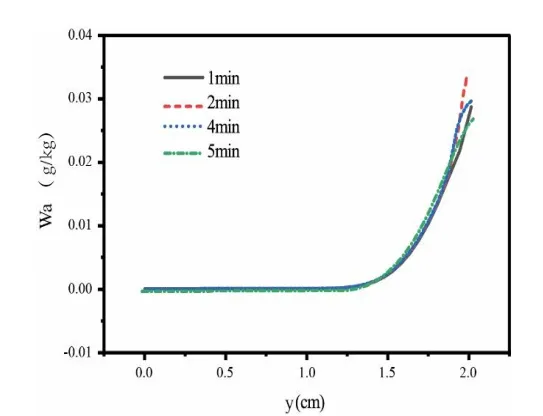
图6 x/L=0.5 处多孔床层不同时刻的径向空气含湿量分布

3.3 空气流速对多孔床传热传质的影响

图7 为空气流速不同时，多孔床沿通道方向平均温度、含湿量分布曲线的数值模拟。随着空气流速的增大，虽然对流换热系数增大，多孔床内温度波动却不明显，换热流体速度过大，还未与床层充分换热，已经流出吸附床，此时造成了热量的浪费。可以看出流速对床层温度影响不大，主要是因为吸附剂导热系数较小，导热热阻较大，虽然增加流速增大了吸附床顶层换热系数，吸附床顶层的温、湿度变化加快，但是对于吸附床底层的多孔介质，床层传热与传质是由传热传质阻力较大的吸附剂所控制。流体流速虽然对床层整体的传热传质影响较小，但是影响系统的热量利用效率，进而影响床层的温度分布。

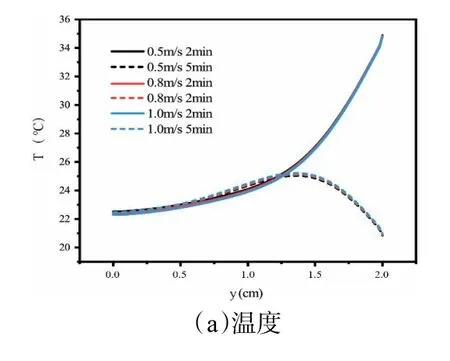
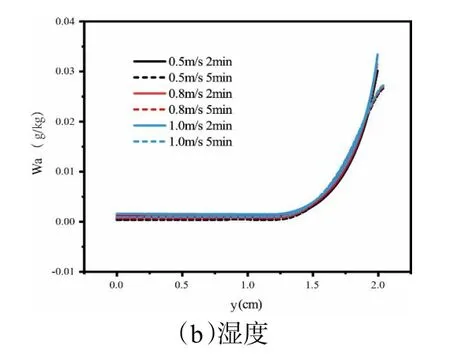
图7 z/L=0.5 处多孔床内空气温度、含湿量的径向分布

4 结论

1）交替变化的边界条件使多孔床顶面出现周期性变化的温、湿度场分布，并且温度和含湿量的变化不是均匀的，热、质交换主要发生在边界条件变换后的 1 min 内，之后的热、质交换量非常少，因此可通过缩短交替周期来提高热、质交换效果。

2）空气与多孔床的热、质交换主要发生在近交界面薄层，对于其他位置影响不大。当使用硅胶作为全热交换材料时，厚度可以不超过5 mm。

3）随着空气流速的增大，对流换热系数增大，多孔床内顶层的温、湿度变化速度变快，但对于吸附床底层的影响效果较弱。