训练空域动态规划问题数值模拟仿真算法研究
2020-05-05张建祥甘旭升孙静娟杨国洲
张建祥,甘旭升,孙静娟,杨国洲
(1.西京学院 理学院,西安 710123) (2.空军工程大学 空管领航学院,西安 710051)
0 引 言
训练空域是提高部队战斗力,增强国防能力的重要载体,近年来,随着武器装备的升级换代和空军部队的战斗转型,日常训练对于空域的需求与日俱增;与此同时,民航事业对空域的需求也急剧增加。军民航之间的用空矛盾愈加突出。因此,训练空域的动态规划对于提高空域资源的利用率和空域灵活使用具有积极的促进作用,同时也可缓解军民航之间的用空矛盾。
对于空域的动态规划问题,国外研究开始较早。2005年,K.Alexander[1]通过对正六边形分割法的改进,在现有分割法的基础上利用雷达历史数据进行空域划分;2009年,G.Sabhnani[2]利用几何算法根据各扇区内空中交通密度的历史数据对扇区进行了动态重组;2012年,D.K.Kumar[3]利用ART1神经网络,结合扇区管制员的工作负荷对扇区进行了重新划分,在为管制人员减压的同时提高了空中交通的管制能力。在德国,空域的灵活使用给军民航协调发展提供了有力支撑,其主张对于预留的军事训练具有优先使用权的空域,在无军事训练的时段可开放给其他用户使用。但由于军方活动的特殊性,无法完全照搬国外的方法。国内对于空域规划的研究大都是有关民航方面的[4],针对空域动态利用的研究主要是从定性的角度分析[5-6]。对于训练空域的动态规划,目前主要依靠参谋的经验,缺乏定量分析,至今没有形成一套高效的规划程序来供部队使用。
战术训练空域动态规划实际上是一种广义的组合优化问题,要求在满足空间约束的前提下,合理安排所有训练任务的开始节点和结束节点,使其在保证空域利用率的同时尽可能缩短空域占用时间。从理论上看,该问题类似于资源调度[7-8]问题,对于此类问题已经得到了广泛的研究,其中遗传算法和整数规划算法占据了主要地位[9-12]。
在规划过程中面临的问题主要有:①由于训练科目种类较多,且各个科目所需的空域大小不同,无法保证空域的利用率;②由于训练任务的繁重和空域资源的有限性,需要分批实施,确定各个科目实施的时间与空间成为难点。
分析 本题题干中涉及到几个新概念.对纠错码理论([5])有了解的读者可以发现,题干中的空间Sn实际上是二元域上的n维线性空间,距离d(A,B)实为纠错码理论中熟知的Hamming距离.毫无疑问,这些概念与情境是考生之前在任何复习参考书上都难以见到的,题目对任何考生来说都是陌生的,有效地保证了考试的公平性.当然,任何考生解答此题无需纠错码理论背景知识,但是肯定需要准确地把握到距离d(A,B) 的意义,即:
本文根据训练空域动态规划问题的特点,将其划分为相互独立又相互联系的多个阶段,每个阶段做出最优决策后再进入到下一个阶段,从而使整个过程的总体决策最优。对于每个阶段,对训练空域进行离散化处理,并通过遗传-粒子群优化算法来搜索寻优得出最优决策。
1 问题描述与数学模型
1.1 问题描述
训练空域是为了保证飞行部队日常训练而划设的空域范围。由于各个科目实施方法的不同,所需的空域大小也不尽相同。战术训练空域的动态规划是指在机场所辖的空域范围之内,合理地安排各批次训练任务,使得在保证空域利用率的同时尽可能缩短所需的总训练时间。其约束条件为:
(1) 每个训练任务一旦开始,必须持续到任务结束;
(2) 所有训练任务必须全部完成;
ZHANG Jian-hua, SHEN Yi, HE Yu-qiong, HAN Ting, QIN Lu-ping, ZHANG Qiao-yan
(3) 所有训练任务必须在机场所辖的空域范围内完成,不得超出空域边界;
(4) 训练任务完成时间以10 min为单位;
(5) 各个训练任务所占空域不得重叠;
(6) 考虑到实际情况,安排各任务所需空域时,需要与坐标轴平行,但可以90°旋转。
1.2 数学模型
针对每一阶段的空域规划,是指在保证空域利用率的基础上,尽可能多地安排训练科目。即在实施过程中,使整个时段内空域的利用率最大。其目标函数为
其中,特征权值在0到1之间。W(i,d)为词i在电子邮件中的权值,if(i,d)为词i在邮件中出现的频率,M是训练集的总数,n为训练集中出现i的内容总数,分母表示归一化因子。
(1)
式中:S为作战责任区内的面积大小;li为某训练科目所需空域的长;wi为某训练科目所需空域的宽;n为该时段内总的训练科目数,且1≤i≤n。
作战责任区会受天气、航路航线、空中限制区等多种因素的影响,因此,作战责任区通常是不规则的,这也增加了空域规划的难度。本文对空域进行离散化处理,同时将其放入直角坐标系当中,放置每个训练科目所需的空域时,需要使其长或者宽与坐标轴平行,并选取其左下顶点为参考点。
原文为:The bar of McGinty's saloon was crowded as usual; for it was the favourite loafing place of all the rougher elements of the town[1]90。
在规划过程中,需要遵循如下约束条件:
(1) 由于战斗机在训练时不得超出划设的训练范围,每个科目必须在作战责任区实施;
Ⅴ Theory of toothpaste raw material (To be continued) 1 64
(2) 各科目之间需要保持一定的距离,不得相互重叠;
(3) 各科目的训练空域需要与坐标轴相互平行,但可以旋转。
具体公式如下:
(2)
(3)
(4)

2 训练空域动态规划的主要方法
训练空域的动态规划是指在机场所辖的空域范围内合理安排训练科目,使其在保证空间利用率的同时尽可能地缩短占用空域的时间。由于空域的有限性,无法同时完成所有科目的训练,将此问题看作时序和空间的双重约束问题。本文通过分阶段处理的方法来解决该问题的时序约束,通过遗传-粒子群优化算法来解决某个时段内的空间约束问题。
2.1 分阶段处理模型
假设有m个相互独立的训练任务j1,j2,…,jm需在机场所辖空域内完成,由于空域资源有限,无法同时完成m个训练任务。将其划分为n个相互独立又相互联系的多个阶段,每个阶段都需要作出相应的最优决策,各个阶段通常按照时间先后顺序进行划分(有科目完成后进入到下一个阶段),阶段变量用k表示。Tks和Tke分别表示该阶段开始时间和结束时间,Tk(i)表示该阶段内正在进行的任务所需完成时间。假设某时段有a个训练任务,则Tke=Tks+min {Tk(1),Tk(2),…,Tk(a)},且T(k-1)e=Tks。通过多阶段处理直至所有的训练任务均完成。再利用遗传-离散粒子群优化算法计算不同方案所需的时间,在保证空域利用率的前提下,选择其中时间最短的一组作为最终的规划方案。
肺炎是一种临床上常见的疾病,主要由细菌和真菌感染引起[1]。随着发展中国家工业化的加剧,环境污染(雾霾、粉尘)常常会引发大量的呼吸道肺部疾病,严重的肺炎可能直接导致病人死亡,尤其是小孩和老人[2-3]。近年来,细菌耐药问题日趋严重并威胁人类健康。目前,临床上抗生素耐药和滥用现象十分严重,已出现超级细菌,仅有几种抗生素对其有效[4]。因此,研究人员迫切寻找新的抗菌物质,开发新型给药系统提高细菌性肺炎治疗效果,减少抗生素耐药。
2.2 基于遗传-离散粒子群优化算法的空域规划法
Step2:将每个粒子的位置与个体最优位置、全局最优位置进行交叉操作,以获取新的染色体,再对新的染色体进行变异操作获得最终个体,同时更新交叉率和变异率。
2.2.1 编码与解码
粒子的编码方式采用整数十进制编码,根据训练科目数生成排放序列,且编码中区分正负,正数表明横放,否则为竖放,默认横放为训练科目的长度大于宽度。每个排放序列根据上方改进的排样算法都能生成一个规划方案,从而确定该方案的适应度值。
2.2.2 转换操作
对于每个可行解的转换操作是通过由多个转换子构成的转换序列来实现的。转换子由2个随机数组成,假设转换子为(ik,jk),Xk为粒子的序列位置,那么对应的转换操作为交换Xk中值为(ik,jk)的位置来得到新的位置。例如,转换序列为{(1,2),(2,3)},序列位置为(1,2,3,4,5),通过转换得到的新位置为(3,1,2,4,5)。应注意,转换序列是按照转换子的位置依次作用在位置序列上的。
2.2.3 粒子更新操作
粒子的更新操作既包括位置的加法操作也包括速度的数乘操作。位置的加法操作是指依照对应的转换序列,对个体的位置进行转换;而速度的数乘操作是指以一定的概率来保留对速度的操作。具体方式如下:
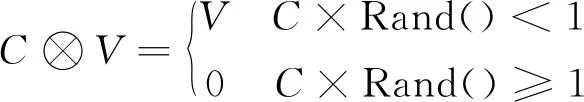
(5)
式中:Rand()为0~1之间的随机生成数。当C=5时,保留概率为20%。
Step5:对每个粒子分别进行两种变异操作,同时求出每个新粒子的适应度值。如果新位置的函数值大于原函数值,则更新个体的最优位置。而对于整个粒子群,每更新一代就选取其中最大的适应度值与上一代进行比较,若大于上一代,则将此位置作为新的全局最优位置。
(6)
≈G×O(N×D)
2.2.4 交叉、变异操作
为了防止算法陷入局部最优,可通过交叉、变异操作增加离散粒子群的全局搜索能力。
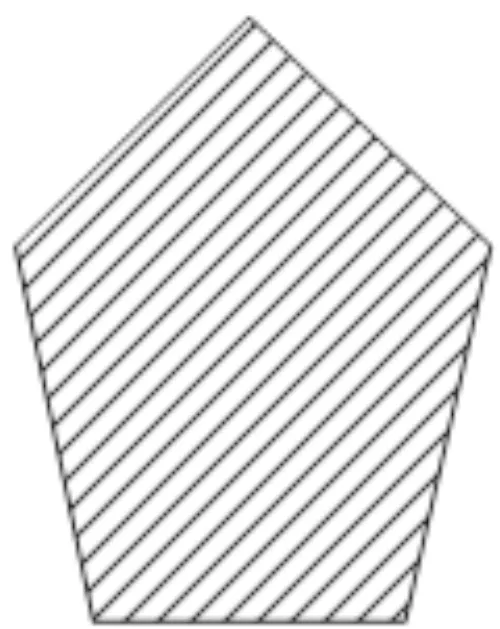
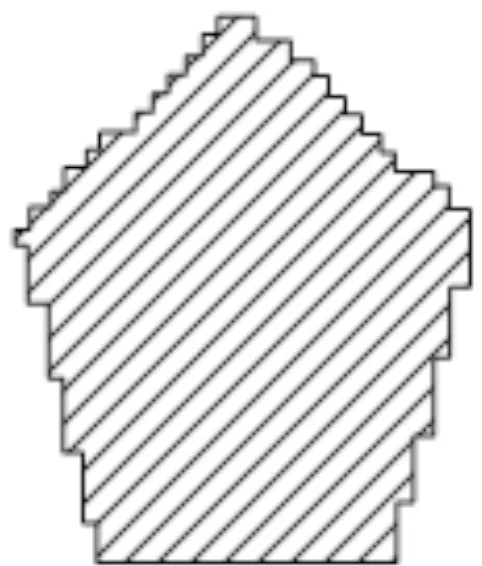
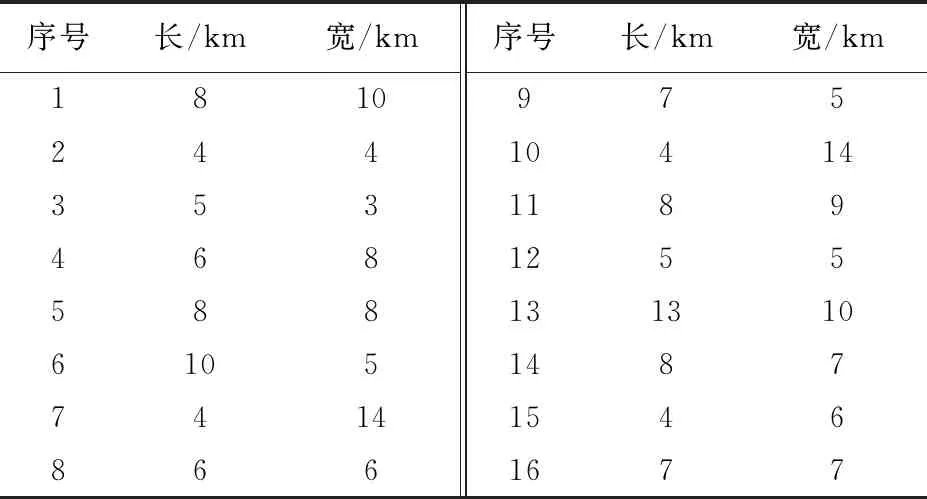
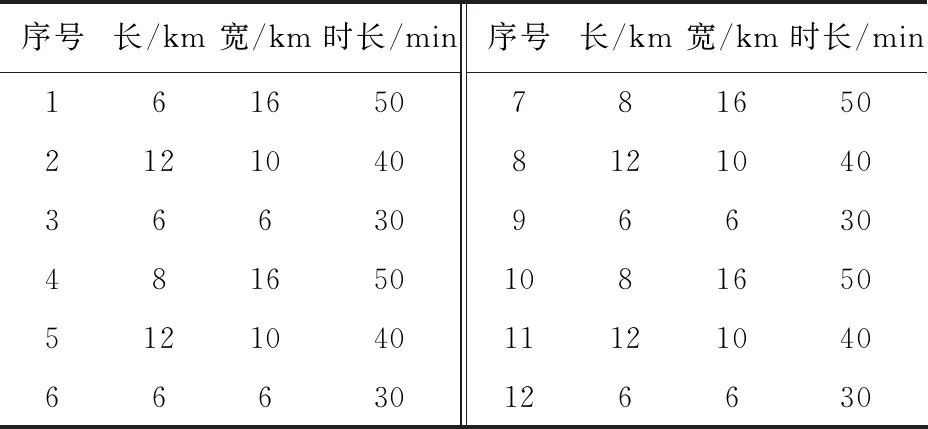
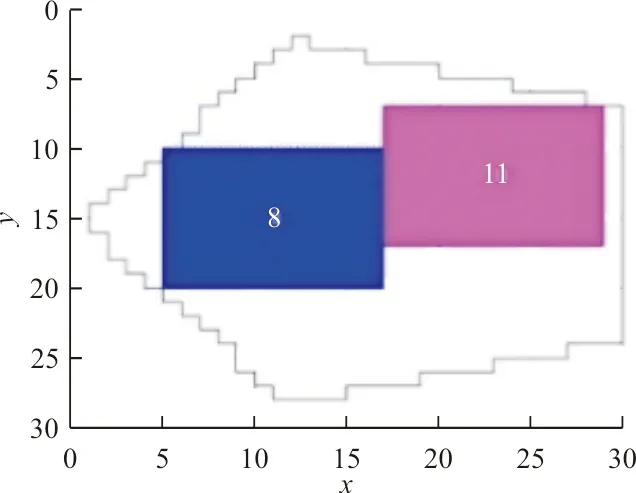
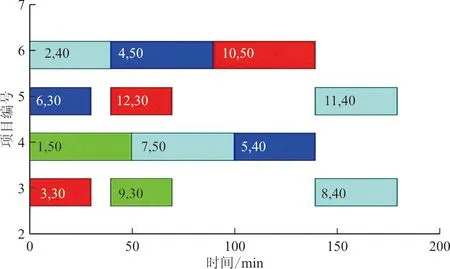
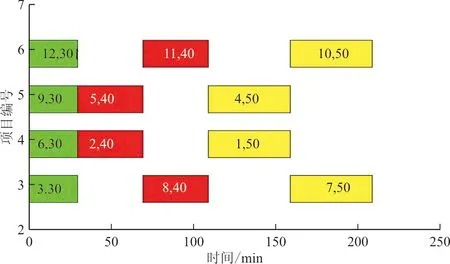
交叉策略为:假设染色体长度为n,交叉概率为Pc,生成一个随机数R,以及变异位r1,r2(r1≠r2,r1≤n,r2≤n)。若R 变异策略为:假设变异概率为Pm,交叉位为rm,随机生成0~1之内的数字O,若O 2.2.5 交叉、变异的自适应性 交叉率和变异率作为遗传操作中的核心操作,为了保证性能较好地基因得以保留、较差的基因尽快剔除。合理地选择交叉率和变异率至关重要。本文对交叉率和变异率做自适应调整,将交叉率的变化值定义为 f(x)=(1-Pc)e(-1/cf) (7) 式中:Pc为当前的交叉概率;cf为剩余的迭代数。 2.2.1 对国有苗圃进行产权改革和产业化重组,将其纳入市场经济轨道,主要是通过产权制度改革,建立能按市场法则办事,彻底抛弃“等、靠、要”的思想,真正成为独立经营、自负盈亏、独立享有民事责任的法人实体,实现经营管理机制由事业性管理转变为以追求经济利益最大化的市场经济运行体制,自觉适应市场竞争要求。并在市场竞争中做强做大,正发挥国有苗圃的龙头和示范带动作用。 导生来自学生,这有利于同学间相互交流。导生本身也在指导过程中获得锻炼,这对他们的能力发展产生了积极的影响。另外,“导生制”实际上也是一种小组教学,对于培养学生的协作学习能力、对话能力、竞争意识都是非常有帮助的,而且有助于在班级内形成浓厚的学习氛围。 f(x)=(1-Pm)e(-1/cf)/10 (8) 式中:Pm为当前的变异率。 2.2.6 算法流程 假定种群的粒子数为m,最大迭代次数为N,Pid为个体最优位置,Pgd为全局最优位置。 Step1:初始化种群,且每个位置均赋予一个初始速度,同时给定相应的参数值。 粒子群优化算法着重解决一些连续、无约束的问题。对于像空域规划这一离散、不连续、有约束的问题仍有较大的研究空间。本文提出用转换子和转换序列来解决离散的规划问题,并引入遗传算法中的交叉与变异思想来提高离散粒子群优化算法中摆脱局部最优解的能力,进而提高算法的收敛速度和精度。通过对当前解与个体最优解、全局最优解的交叉变异操作,在解空间中产生新的位置。同时为了保证种群的多样性和个体的适应性,用自适应递阶算法来控制交叉率和变异率。 Step3:利用改进的排样算法解码粒子并求其适应度值F,将其作为粒子的初始个体最优位置Pid,选取其中适应度最大的位置作为全局最优位置Pgd。 变异率的值定义为 Step4:按照算法中粒子的更新方法更新粒子的位置。 而在离散粒子群中,粒子更新如下: Step6:当迭代次数达到设定的最大迭代次数或者适应度不再发生变化时,终止该算法,并根据最优的规划方案画出空域规划图。 算法复杂度不仅决定了算法的执行效率,而且在极大程度上影响着算法的求解能力。相较于基本离散粒子群优化算法,改进后的算法增加的计算时间主要用于粒子的交叉和变异。假设问题的规模为D,种群的大小为N,迭代次数为G,对于基本的粒子群优化算法需要更新粒子的位置和速度,并计算相应的适应度值及保留最优个体,其计算时间复杂度为 在求解过程中,假定粒子群的种群个数为20,迭代次数为100代,个体经验保留概率c1=2,全局经验保留概率c2=2,w=1,变异概率Pm=0.1,交叉概率Pc=0.9。通过仿真,发现当迭代到第73代时已经趋于稳定,而此时的适应度值为11.855 3,最后生成的空域训练图以及在迭代过程中每代的最优适应度值和平均适应度值的变化过程如图3~图4所示,交叉率、变异率的变化如图5所示。 O(N,G,D)=3G×O(N×D)+G×O(N) 式中:w、C1、C2分别为速度保留概率、全局最优值和个体最优值对进化的影响因数。 “不想,我只想我的程江,程江出差四天了,说好今天回来的啊,怎么到现在还不回来,他爱吃的红烧肉我都做好了。”李莉打断梅子的话,佯装看着窗外。 (9) 而改进算法的复杂度为 O(N,G,D)=3G×O(N×D)+G×O(N)+ (Pc+Pm)G×O(N×D) ≈G×O(N×D) (10) 可以看出:算法的计算时间复杂度仅与求解问题的规模D、种群规模N和迭代次数G有关,改进以后的算法并没有明显增加算法的计算时间复杂度。 甘特图,也称为条状图,其主要目的是为了显示工作进度随着时间进展的情况[13-14]。其横轴表示时间,纵轴表示作业,线条表示各个工作任务的完成情况。通过甘特图可以直观地看出某个任务的开始时间和结束时间,并评估该任务的进行情况。甘特图具有清晰明确的特点,是控制工作进度的工具,其绘制方法也非常灵活,具体方法详见参考文献[15]。本文利用甘特图来表示各个训练任务随时间的进展情况,并通过Matlab软件进行绘制。 为了评估本文提出的算法对于解决战术训练空域动态规划问题的有效性,进行实例仿真。实例一为了检验遗传-粒子群优化算法的有效性,实例二为了检验空域动态规划的可行性。 基于某飞行部队日常训练进行仿真,该部的作战责任区及其离散化处理后的空域图如图1~图2所示。 图1 训练空域图Fig.1 Training airspace figure 图2 离散训练空域图Fig.2 Discrete training airspace figure 假定某天所进行的训练科目及其所需空域大小如表1所示。 表1 各训练科目所需空域大小 “物”的三重规定性是一个统一的整体。在其中,“物”的实践论的规定性是根本性的,因为实践是人和“物”、自然和历史分化和整合的基础,也是社会关系形成的基础。而且,只有在实践论的语境中,谈“物”的社会政治意蕴才是合法的。“物”的社会性的规定性在一定程度是实践论的规定性的现实表现和具体展开,同时从关系论的角度丰富了前者。“物”的政治经济学的规定性(即作为物化力量的“物”),则是第二重规定性在资本主义社会中的具体表现,是对第一重规定性的更为具体的展开。这三重规定性共同说明了“物”与人、社会、历史本就是统一的,尽管也是对立的,并在有些情况下表现出分裂。 图3 战术训练空域规划图Fig.3 Planning diagram of tactical training airspace 图4 适应度值变化曲线图Fig.4 Curve of fitness value change 图5 变化率曲线图Fig.5 Curve of change rate 而用传统的粒子群优化算法进行求解时,假定参数相同,通过仿真发现:当迭代到第90代时,基本趋于稳定,而此时的适应度值为10.789 9,最后生成的空域训练图以及在迭代过程中每代的最优适应度值和平均适应度值的变化过程如图6~图7所示。 图6 战术训练空域规划图(传统方法)Fig.6 Planning diagram of tactical training airspace (traditional method) 图7 适应度值变化曲线图(传统方法)Fig.7 Curve of fitness value change(traditional method) 通过对比可以发现: 意识的培养不是一蹴而就的,长期潜移默化的影响才能形成稳定的意识形态。面对我国高校创新创业教育滞后和师资不足的现状,光靠几节创新创业课程是不能有效激发师范生创新创业意识的。只有在日常的教学过程中,教师有计划的创新创业意识渗透与灌输才能提高教育成效。 (1) 利用遗传-离散粒子算法得到的训练空域规划方案对空域的利用率更大,且在作战责任区内安排的训练科目数也更多,提高了算法全局搜索的能力; (2) 通过比较两组数据趋于稳定时的代数,发现传统粒子群优化算法的搜索性能要明显弱于遗传-离散粒子群优化算法,利用遗传-离散粒子群优化算法求解时,在第73代就可以得到趋于稳定的解,表明算法改进后收敛能力更强。 综上所述,两种算法均可用于求解训练空域的规划问题,但离散-粒子群优化算法的求解性能要优于传统的粒子群优化算法。 假定某部某天需完成3种战术训练任务,每个任务均有4个批次(m=12),其训练任务的时长及所需空域大小如表2所示。 随着生猪养殖事业向集约化、规模化的方向发展,对饲养管理人员提出了更高的要求,养猪户不仅要掌握生猪生产动态,还需要全面提升科学饲养管理水平,最大程度地减少市场风险。地区各级政府部门需要强化养猪户的培训,确保自产自销养殖户能掌握饲养管理技术,逐步增强自身的防疫意识,全面提升养殖人员的综合素质与专业技能。确保自产自销养殖户精准掌握市场经济脉搏,全面提升自身的养猪技能水平。政府部门可每月制定1次养殖人员培训,促使养殖人员的专业技能与综合素质得到全面提升,确保生猪自产自销防疫工作开展的有序性,全面提升生猪养殖经济效益[4]。 选矿厂不间断的生产过程就是数据的不间断生产过程,获取选矿大数据是利用大数据的前提。目前我国很多选厂数据来源主要是有经验的工人掌握的生产经验数据和技术人员生产取样数据,其中有的数据量化难度大,可靠性不强,受制于个人的经验差别很大。而在实际工业生产中,由于入选矿石品位波动,矿石性质变化,药剂用量等发生变化,导致生产数据规律不断波动。利用现代感知技术和人工智能设备可以挖掘积累大量有效数据,将其用大数据技术分析获得的结果用于分析指导生产和评估技术经济指标具有重大意义。 表2 训练任务所需空域大小及时长 应用本文算法对此问题求解,通过计算可得,完成上述训练任务需要分6个阶段,各阶段空域规划如图8~图13所示。 图8 第一阶段空域图Fig.8 Airspace diagram at the first stage 图9 第二阶段空域图Fig.9 Airspace diagram at the second stage 图10 第三阶段空域图Fig.10 Airspace diagram at the third stage 图11 第四阶段空域图Fig.11 Airspace diagram at the fourth stage 图12 第五阶段空域图Fig.12 Airspace diagram at the fifth stage 图13 第六阶段空域图Fig.13 Airspace diagram at the sixth stage 训练进度随时间变化的进展情况(甘特图),如图14所示。 图14 训练进度图Fig.14 Training schedule 从图14可以看出:先进行第1,2,3,6号训练任务,第40 min执行第4,9,12号训练任务,第50 min开始执行第7号任务,第90 min开始执行第10号任务,第100 min进行第5号训练任务,最后在第140 min进行第8和第11号训练任务。 目前,战术训练空域主要依靠人为经验进行划设,仅能够按照训练任务的种类依次进行,其训练进度随时间的变化如图15所示。 图15 当前训练进度图Fig.15 Current training schedule 从图15可以看出:相较于依靠人为经验划设,利用本文算法可以更快地完成所有训练任务,训练时间由210 min缩短到了180 min,节约了30 min;利用本文方法在实现动态任务规划的同时,还能够保证空域利用率和用空安全,给空域的灵活使用提供了一定的借鉴;利用计算机进行辅助设计,可大幅缩短空域规划所需时间,提高规划效率。 随着军民航飞行需求的增加和民用航空的蓬勃发展,现有的空域资源分配方式已然无法满足日常的用空需求。针对训练空域的规划问题,本文融合了遗传算法中的交叉变异思想,提出了遗传-离散粒子群优化算法。与传统的粒子群优化算法相比,本文的新颖之处在于:①利用遗传算法中的交叉与变异思想来提高算法的收敛速度;②引入了自适应交叉与变异算子,提高了搜索的广度与深度,保证了种群的多样性。 将训练空域规划问题进行分阶段处理,并利用甘特图来表示整个空域利用过程,在保证空域利用率的同时,能够尽可能地缩短空域占用时间;相较于目前的人为划设规化法,利用该方法可以大幅缩短训练所需时间,不仅能够提高飞行效率,而且能够有效缓解军民航的飞行冲突;但该算法的稳定性和求解效率还有待进一步研究和改进。2.3 算法复杂度分析
2.4 甘特图
3 训练空域动态规划实例仿真
3.1 某一阶段的空域规划问题

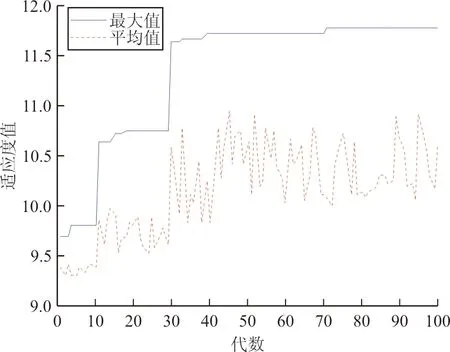

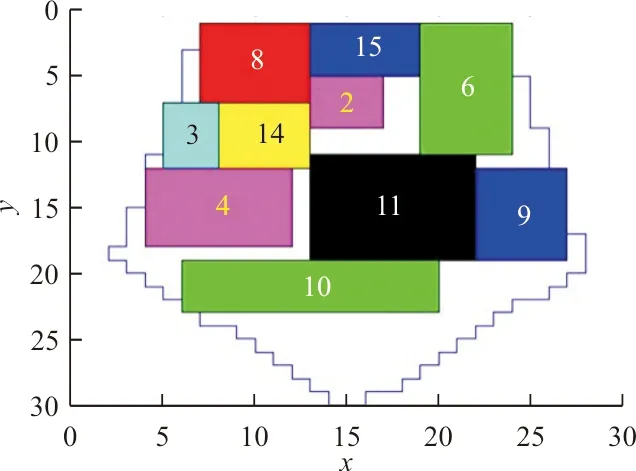
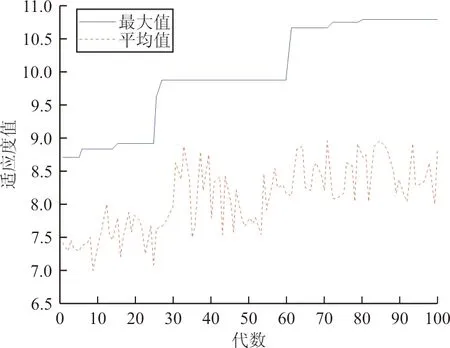
3.2 多时段的空域规划问题
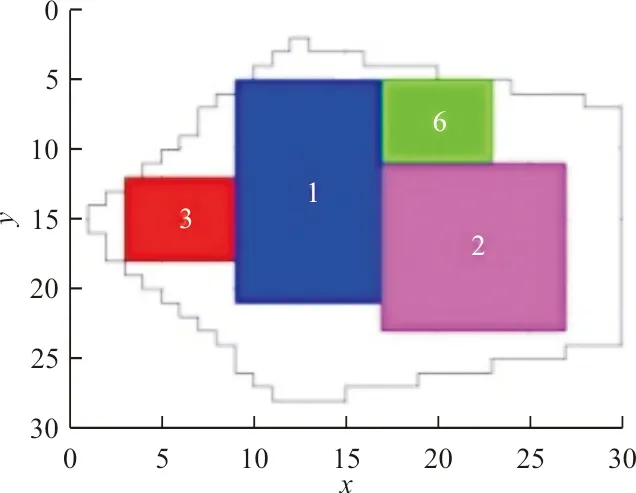

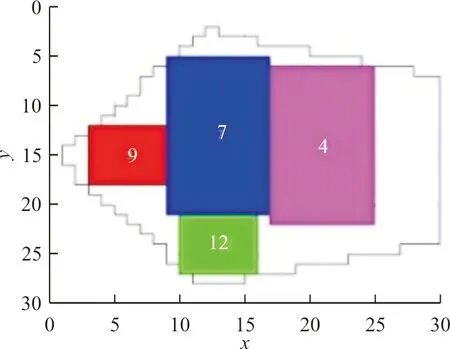
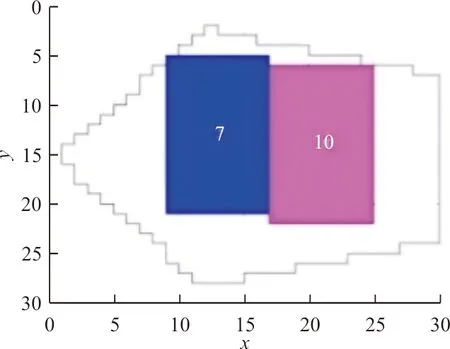
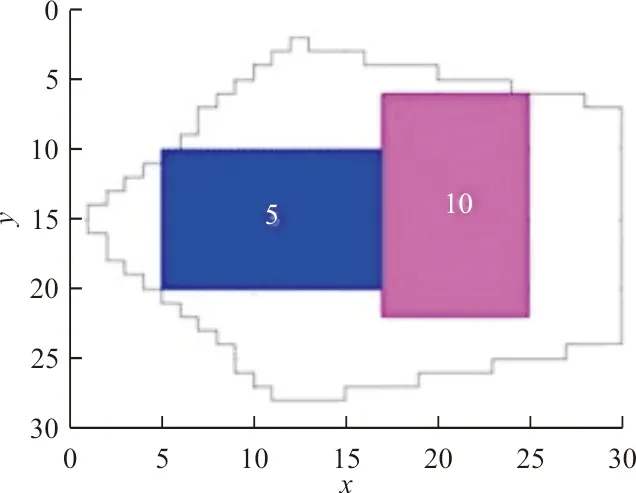
4 结 论
