纵列式直升机双旋翼气动特性分析

陈建炜，朱清华，王坤，朱振华，申遂愿

(南京航空航天大学 直升机旋翼动力学国家级重点实验室，南京 210016)

0 引 言

与常规单旋翼直升机相比，纵列式直升机具有诸多优势，比如更加紧凑的结构，更大的载重量，更强的抗侧风能力，更高的悬停效率，允许较大的重心变化范围等。这些优点决定了纵列式直升机具有广阔的应用前景，军事上，可应用于机降部队、弹药投送、舰船补给、吊运大型武器装备等方面，民用方面，适用于灾后物资运送、灾民转移、油气开发、森林灭火等方面[1-4]。因此，对纵列式直升机的理论研究具有重要的现实意义。随着国民经济的发展，国内对于重型直升机以及无人运输机的需求日益凸显，纵列式直升机将成为未来发展的一个热点。

然而，纵列式直升机前后两个旋翼一般会有一定的重叠，其尾迹流场和气动特性与常规单旋翼直升机有很大区别。无论是悬停状态还是前飞状态，前后旋翼之间都会产生严重且复杂的气动干扰现象，造成性能损失的同时，还影响直升机安全飞行。因此，前后旋翼间的气动干扰问题一直是纵列式直升机的一个重要的研究课题。早期的理论研究主要采用涡方法，A.Bagai等[5]首次使用自由尾迹方法对纵列式直升机两旋翼进行了尾迹分析；D.A.Griffiths[6]采用自由尾迹模型分析了两旋翼的干扰流场与地面效应；黄水林[7]采用自由尾迹方法对纵列式直升机双旋翼气动干扰特性进行了研究。然而，涡方法无法捕捉干扰流场的细节特征，这给进一步深入研究带来了困难。近年来，CFD方法发展迅速，在纵列式双旋翼干扰流场的模拟上也有所应用。Tong Z等[8]基于N-S方程对共轴、纵列式双旋翼干扰特性展开了研究；A.Dimanlig等[9]采用嵌套网格方法对CH-47模型进行了数值模拟；吴林波[10]采用基于Euler方程与动量源模型的CFD方法开展了纵列式双旋翼/机身流场研究。然而，针对纵列式双旋翼直升机的CFD研究还处于起步阶段，以往的研究多存在未考虑空气粘性或耗时过长的问题，且这些研究基本没有对干扰下前后旋翼气动现象产生的原因进行更深入的研究。

鉴于此，本文采用高效的动量源方法，基于N-S方程和k-ωSST湍流模型，对纵列式直升机两旋翼间的气动干扰问题进行数值研究。首先，使用本文建立的数值方法，对悬停状态单旋翼进行计算，验证本文所建立方法的可靠性；然后，对悬停状态两旋翼干扰流场进行计算，并在随后的模拟中加入来流，对孤立旋翼状态、双旋翼流场前向来流状态与后向来流状态分别进行计算；最后，在计算结果的基础上，结合流场特性，对前后旋翼相互干扰下气动现象产生的原因进行分析，得出具有实际意义的结论，以期为纵列式直升机的研制提供一定的技术支持。

1 数值方法

1.1 动量源方法与控制方程

本文采用动量源方法模拟纵列式直升机旋翼流场，将旋翼产生的气动力以动量源的形式加载在桨盘上，并假设此时旋翼的周期性转动为“准定常”流动。采用该方法在大幅提高计算效率的同时，保证了旋翼下洗流场的本质属性[11-12]。

加载在桨盘上的动量源项[13]为

(1)

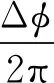
本文所研究的旋翼转速较低，桨尖马赫数为0.17，因此采用有粘不可压缩流体假设，控制方程采用包含动量源项的N-S方程[14]。

其中，连续性方程与X方向动量守恒方程均采用微分形式，分别为

(2)

(3)

Y和Z方向的动量守恒方程以此类推。

1.2 湍流模型及边界条件

采用FLUENT流体计算软件对两旋翼干扰流场进行计算，选用基于压力隐式求解器，控制方程使用二阶迎风格式的有限体积法进行离散，在湍流模型的选择上，采用k-ωSST两方程湍流模型[15]，该模型对涡流场具有较高的捕捉精度，在两旋翼干扰流场的模拟上具有良好的表现[16-18]。

远场边界条件采用无反射边界条件，采用一维Riemann不变量来保证远场边界满足该条件，Riemann不变量可以表示为

(4)

式中：α为当地声速；Vn为远场边界处流出速度的法向分量[19]。

1.3 计算模型与网格划分

旋翼参数如表1所示，计算域直角坐标系原点位于前旋翼桨毂中心，后旋翼桨毂中心处于ZOY平面。定义前旋翼旋向为逆时针，后旋翼旋向为顺时针。本文主要研究前后旋翼间的干扰，因此忽略了机身对流场的影响。

表1 数值模拟旋翼参数

计算域网格采用混合网格，桨盘处为结构网格，外流场采用非结构网格。直升机旋翼几何模型如图1所示，网格划分示意图如图2所示。

图1 直升机旋翼几何模型Fig.1 Geometry model of helicopter rotor

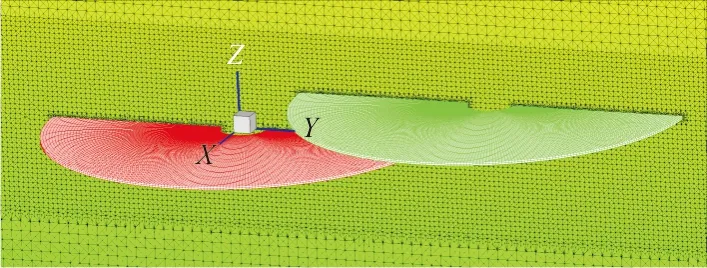
图2 旋翼流场网格示意图Fig.2 Rotor flow field grid diagram

2 动量源方法算例验证

为了验证本文所建立的数值研究方法的可靠性，以NASA ROBIN旋翼[20]悬停状态为算例，将桨盘下方0.215R处动压分布试验数据与本文计算结果进行对比。动压分布如图3所示。

图3 桨盘下方动压分布Fig.3 Dynamic pressure distribution under the rotor disk

从图3可以看出：桨盘下方0.215R处动压分布计算结果与试验值趋势基本一致，表明本文建立的基于动量源模型的数值模拟方法能准确预测旋翼下洗流场。

3 数值模拟及流场特征分析

为了更直观地表现两旋翼的干扰作用对旋翼性能的影响，定义升力干扰系数KL，其为干扰作用下前、后旋翼计算升力与对应流场情况下单旋翼升力之比，计算公式为

KL1(2)=L1(2)/Lisolated

(5)

定义前、后旋翼效率计算公式：

(6)

为了表现前后旋翼的干扰作用对纵列式双旋翼直升机系统性能的影响，定义双旋翼效率计算公式：

(7)

式中：L为旋翼升力；CL为旋翼升力系数；mK为旋翼功率系数。

3.1 悬停状态流场分析

针对纵列式直升机悬停状态，使用本文建立的数值模拟方法对两旋翼之间的气动干扰进行数值模拟，并结合计算结果与流场特性，对气动干扰现象进行了分析。

纵列式直升机两旋翼升力干扰系数随轴向间距的变化如图4(a)所示，此时固定两旋翼纵向间距Y/R=1.3，轴向间距Z/R在0.1～0.3变化。可以看出：受两旋翼相互干扰作用，前后旋翼升力干扰系数均小于1，即两旋翼升力均小于单旋翼状态，且后旋翼升力始终大于前旋翼；随着轴向间距增大，后旋翼升力增加，前旋翼升力降低，最低处升力损失为8.6%。

纵列式直升机两旋翼升力干扰系数随纵向间距的变化如图4(b)所示，此时固定两旋翼轴向间距Z/R=0.2，纵向间距Y/R在1.1～2.1变化。可以看出：随纵向间距增大，前旋翼升力变化较大，总体上呈增大趋势，在Y/R=1.9时达到最大值，高于Y/R=1.1时9.3%，且此时前旋翼的升力超过了后旋翼；后旋翼升力变化不大，总体上呈降低趋势。

(a) 随轴向间距变化

(b) 随纵向间距变化图4 升力干扰系数随间距的变化(悬停状态)Fig.4 Interaction factor of lift v.s. rotor separation (Hovering state)

旋翼效率随前后旋翼轴向间距与纵向间距的变化如图5所示，图中分别给出前后旋翼与双旋翼的效率变化。可以看出：由于干扰的存在，前后旋翼效率均小于单旋翼状态，随轴向间距增大，前旋翼效率基本不变，后旋翼效率增加，两旋翼效率也略有增加；随纵向间距增大，前旋翼效率增加，最低处在Y/R=1.1处，低于单旋翼状态10.3%，最大效率出现在Y/R=1.9处；后旋翼效率总体上呈降低趋势；同时，前旋翼、后旋翼、双旋翼效率曲线相交于一点，这与文献[21]中带负扭旋翼的试验结果相一致，本文算例相交于Y/R=1.74处。

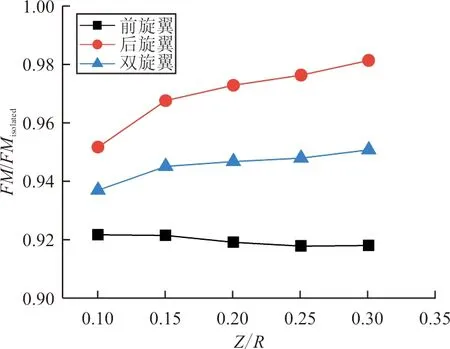
(a) 随轴向间距变化

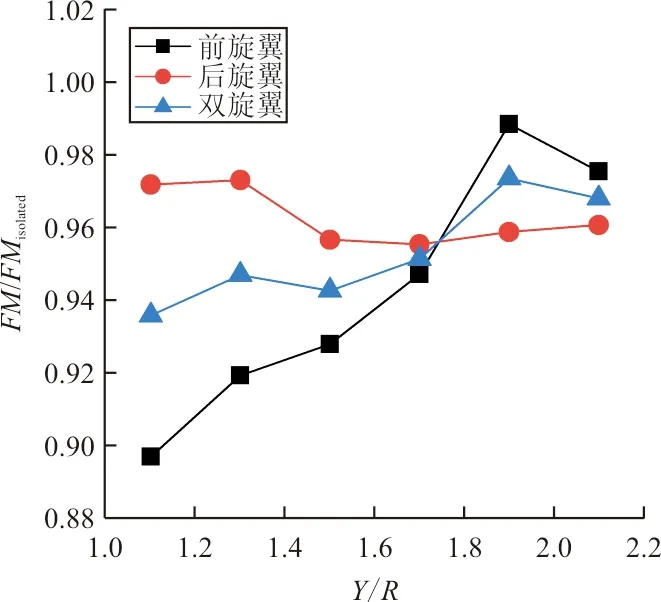
(b) 随纵向间距变化图5 旋翼效率随间距的变化(悬停状态)Fig.5 Rotor efficiency v.s. rotor separation (Hovering state)

Z/R=0.2，Y/R=1.1与Y/R=1.9处纵列式直升机前后旋翼桨盘诱导速度分布云图如图6所示，可以看出：在Y/R=1.1状态，受后旋翼的下洗流影响，前旋翼在与后旋翼投影重叠的部分诱导速度明显增大，这是导致此时前旋翼升力损失的主要

原因，而后旋翼桨盘诱导速度受前旋翼影响较小；在Y/R=1.9状态，由于前后旋翼投影重叠区域减小，前旋翼桨盘处诱导速度基本不再受后旋翼影响。

(a) Y/R=1.1状态

悬停状态ZOY剖面速度流线图如图7所示，在Y/R=1.1时，前旋翼在桨盘投影重叠侧产生明显的桨尖涡，这也是导致升力损失的一个原因；而在Y/R=1.9时，后旋翼的尾迹边界刚好处于前旋翼桨尖附近，前旋翼桨尖涡消失，后旋翼对前旋翼桨尖产生有利效应，此时旋翼升力与效率增大，这与文献[22]中横列式直升机的气动干扰现象相一致。

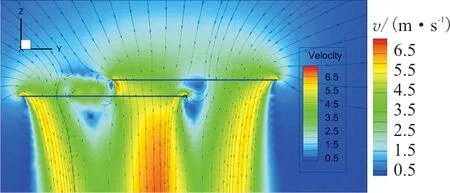
(a) Y/R=1.1状态

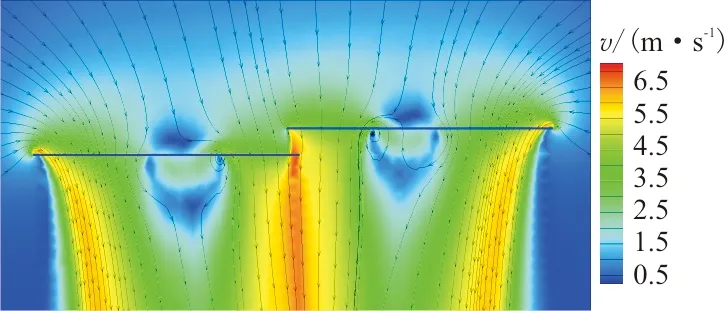
(b) Y/R=1.9状态图7 悬停状态速度流线图Fig.7 Velocity streamline of hovering state

Z/R=0.2状态ZOY截面前旋翼桨盘处下洗诱导速度分布如图8所示，体现了不同纵向间距下后旋翼对前旋翼的干扰作用。可以看出：前后旋翼投影重叠区域诱导速度明显增大，最大下洗普遍出现在后旋翼桨尖下方，诱导速度的变化直接导致前旋翼升力与效率的变化。

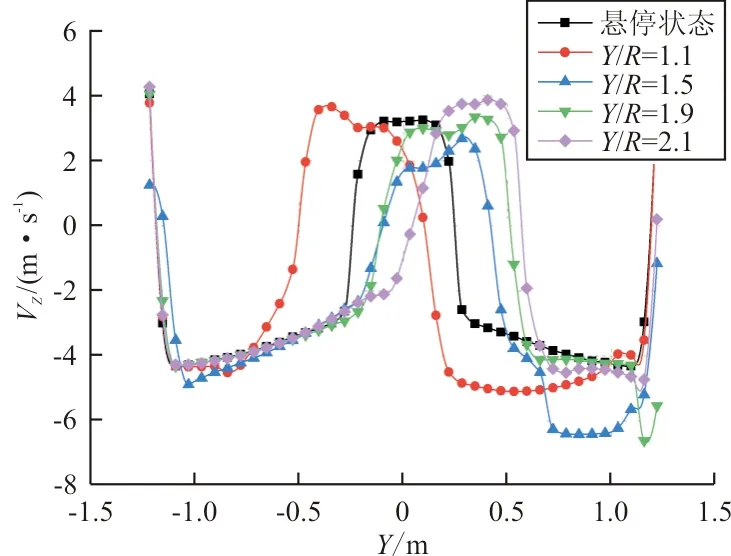
图8 前旋翼桨盘处诱导速度分布Fig.8 Induced velocity distribution at the front rotor disk

3.2 有来流状态流场分析

3.2.1 前向来流状态

在流场中加入前向来流，给定来流速度6、10 m/s，方向沿Y轴正向，即模拟纵列式直升机迎风状态。

6 m/s来流作用下前后旋翼的升力干扰系数随两旋翼相对位置的变化如图9所示，可以看出：在来流作用下，前旋翼的升力始终高于后旋翼，这与悬停状态的模拟结果截然相反；随着轴向间距的变化，前旋翼升力略大于单旋翼状态，且基本不受轴向间距变化的影响；后旋翼升力随轴向间距增大而增大，最低处为Z/R=0.1时，升力损失为16%；随旋翼纵向间距增大，前旋翼升力基本不受后旋翼影响，后旋翼升力增大，最大升力损失为11.9%。

(a) 随轴向间距变化

(b) 随纵向间距变化图9 升力干扰系数随间距的变化(前向来流速度为6 m/s)Fig.9 Change for interaction factor of lift with rotor separation(Flow speed in front is 6 m/s)

前向来流状态下旋翼效率的变化如图10所示，可以看出：由于前旋翼的干扰作用，后旋翼效率显著降低；随着轴向间距的增大，前旋翼效率略大于单旋翼状态，且基本不变，后旋翼效率增加，最低处效率仅为单旋翼状态的65.5%；而随着纵向间距的变化，旋翼效率基本不变，此时由于前后旋翼的干扰作用，两旋翼总体效率下降了约15%。

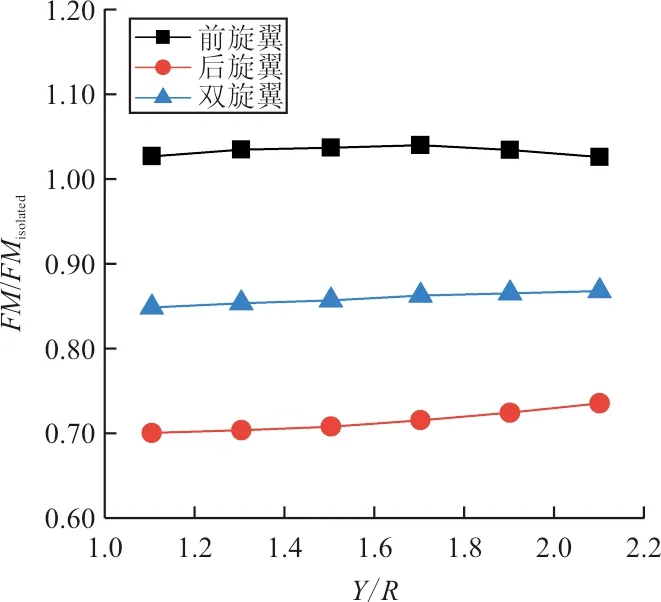
(b) 随纵向间距变化图10 旋翼效率随间距的变化(前向来流速度为6 m/s)Fig.10 Change of rotor efficiency with rotor separation (Flow speed in front is 6 m/s)

10 m/s来流作用下前后旋翼的升力干扰系数与效率随两旋翼相对位置的变化分别如图11～图12所示。

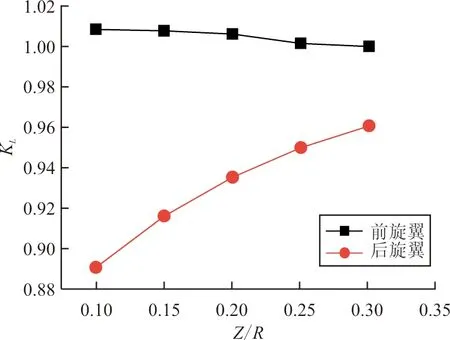
(a) 随轴向间距变化

(b) 随纵向间距变化图11 升力干扰系数随间距的变化(前向来流速度为10 m/s)Fig.11 Change of interaction factor of lift with rotor separation(Flow speed in front is 10 m/s)

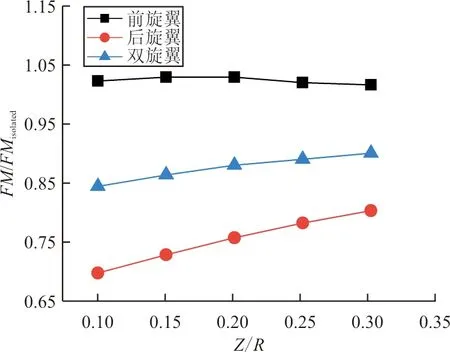
(a) 随轴向间距变化

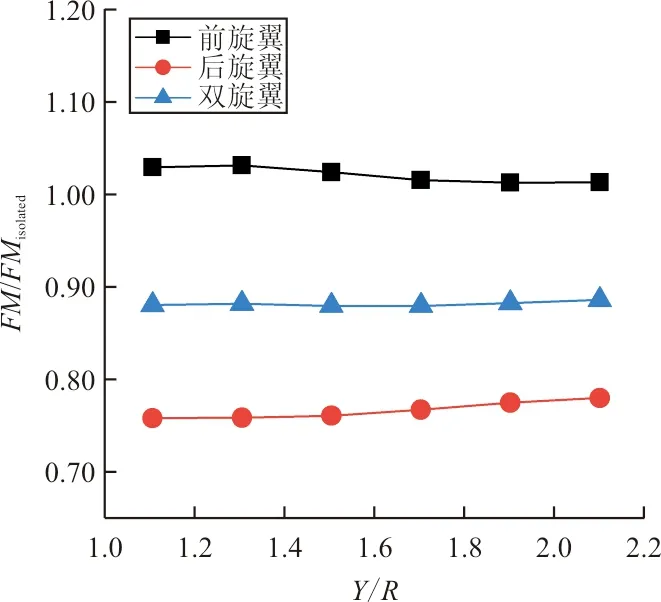
(b) 随纵向间距变化图12 旋翼效率随间距的变化(前向来流速度为10 m/s)Fig.12 Change of rotor efficiency with rotor separation (Flow speed in front is 10 m/s)

从图11～图12可以看出：在10 m/s来流作用下，前旋翼的升力干扰系数与效率始终高于后旋翼，其变化趋势与6 m/s前向来流状态基本一致，但相比之下后旋翼的升力干扰系数显著增大；最低效率出现在Z/R=0.1，Y/R=1.3处，为单旋翼状态的69.9%，大于相同位置6 m/s来流状态，即此时前旋翼对后旋翼的干扰作用减小。

ZOY平面Z/R=0.2，Y/R=1.3处6、10 m/s前向来流状态下的速度流线图如图13所示，可以看出：在来流的作用下，前旋翼尾迹倾斜，对后旋翼产生了明显干扰，随着前飞速度增大，干扰减小，而后旋翼对前旋翼的流场影响很小。这解释了上文前向来流作用下前后旋翼的升力与效率的变化趋势。

(a) 6 m/s前向来流状态

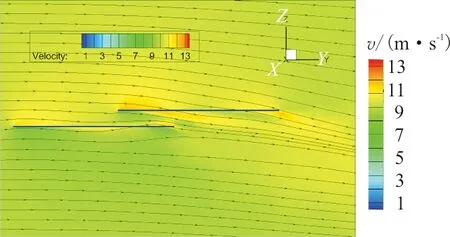
(b) 10 m/s前向来流状态图13 前向来流状态速度流线图Fig.13 Velocity streamline of forward flow state

3.2.2 后向来流状态

后向来流速度为6 m/s，方向沿Y轴负向，模拟纵列式直升机在悬停状态下受后向来流影响。升力干扰系数如图14所示，可以看出：与前向来流状态相反，后旋翼升力与单旋翼状态基本重合，而前旋翼产生了较大的升力损失，最大损失达28.9%，远大于相同来流速度下前向来流状态后旋翼的升力损失；随着轴向间距增大，前旋翼升力降低，这与其他状态的模拟结果截然相反。

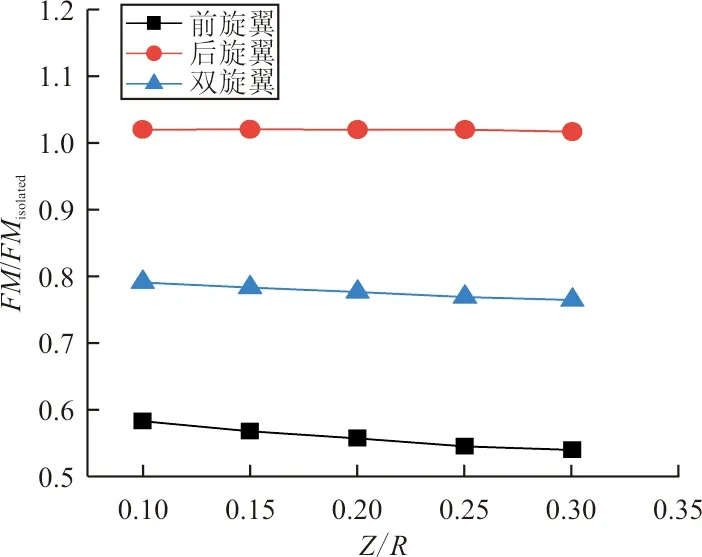
此时旋翼效率的变化曲线如图15所示，可以看出：后旋翼效率与单旋翼状态基本一致，前旋翼最低效率仅为单旋翼状态的54.2%，双旋翼总体效率损失普遍达到20%以上，可见此状态前旋翼所受干扰是很严重的。

(a) 随轴向间距变化

(b) 随纵向间距变化图14 升力干扰系数随间距的变化(后向来流速度为6 m/s)Fig.14 Interaction factor of lift v.s. rotor separation (Backward flow speed is 6 m/s)

(a) 随轴向间距变化

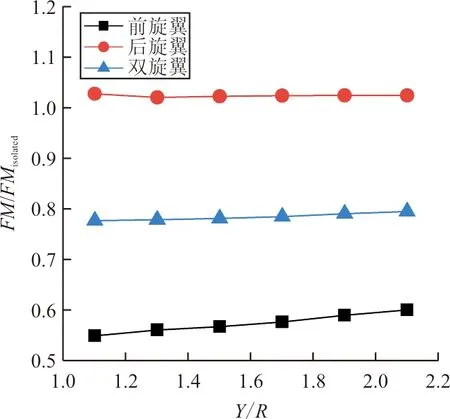
(b) 随纵向间距变化图15 旋翼效率随间距的变化(后向来流速度为6 m/s)Fig.15 Rotor efficiency v.s. rotor separation (Backward flow speed is 6 m/s)

后向来流速度为6 m/s时，速度流线图如图16所示，旋翼桨盘处诱导速度分布云图如图17所示，可以看出：此时后旋翼向前倾斜的尾流直接作用在前旋翼上，前旋翼桨盘下洗诱导速度明显增大，直接导致前旋翼升力损失，而后旋翼处于前旋翼尾流的上方，因而受前旋翼干扰影响较小；随着轴向间距增大，前旋翼受后旋翼下洗流影响范围扩大，升力损失更明显。

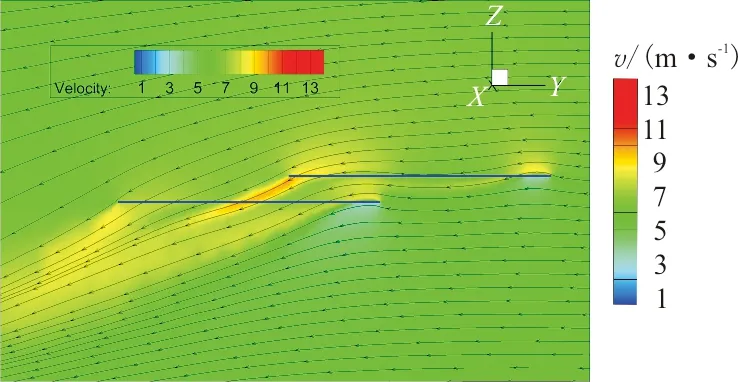
图16 后向来流状态下速度流线图Fig.16 Velocity streamline of backward flow state

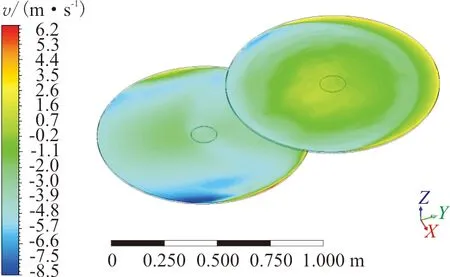
图17 旋翼桨盘处诱导速度分布云图(后向来流状态)Fig.17 Induced velocity distribution at the rotor disk (Backward flow state)

4 结 论

(1) 本文建立的基于动量源模型和N-S方程，采用k-ωSST湍流模型的数值研究方法，能准确预测旋翼下洗流场。

(2) 在悬停状态，纵列式直升机前后旋翼的干扰作用会降低旋翼的升力与效率，前旋翼受后旋翼下洗流影响较大，最大升力损失为10.3%。

(3) 在悬停状态，随着两旋翼纵向间距增大，前旋翼升力增大，直至超过后旋翼升力。在Y/R>1.74后，后旋翼下洗流会对前旋翼桨尖产生有利效应，前旋翼效率开始大于后旋翼。

(4) 前向来流状态，前旋翼尾迹倾斜，对后旋翼产生较大干扰，轴向间距越大，干扰越小。在6 m/s来流速度下，后旋翼最大升力损失为16%，当速度达到10 m/s，前旋翼对后旋翼干扰作用减小。

(5) 后向来流状态，后旋翼尾迹直接作用在前旋翼桨盘处，对前旋翼产生严重干扰，最大升力损失达28.9%，最低效率仅为单旋翼状态的54.2%。

(6) 本文建立的动量源模型未计入来流下旋翼的挥舞运动，与实际情况会存在一些偏差，但前后旋翼相互干扰的总体变化趋势与干扰作用下的流场特性可供读者参考。