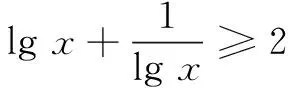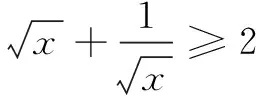学懂学通 灵活运用

刘顺亮

(山东省济南市济阳区第一中学，251400)

新高考要求下的数学试题,探究性与开放性的要求肯定会越来越高,仅靠搞“题海战术”已很难奏效.这就要求我们必须在复习备考中踏踏实实地开展探究性学习活动,让学生亲自动手,真正学懂学通,学会对知识的自主构建，学会自主学习，不断创新，提高应用能力，从而适应新形势下的高考要求.下面以基本不等式这一知识点的教与学为例谈一下个人的认识和实践.

基本不等式是“不等式”一章中的重要内容之一,它是求函数最值的一个重要工具,也是高考常考的一个重要知识点.前面学生已经初步了解基本不等式，但尚未弄懂弄通和灵活运用，需要加深理解.

一、设计练习题

求下列函数的最值：

(可以先选4名学生上台板演,其余学生在座位上练习.学生做完题目后,再根据出现问题灵活处理.

学生对这一组练习完成的情况：第1题基本正确，说明学生对基本不等式已初步了解，会直接运用.而其余3道练习题学生出现的问题和错误可能较多.一是只会直接运用基本不等式，对于需要创造(定值)条件应用基本不等式的题型不知如何下手(如第2题)；二是不注意应用基本不等式的“正数”条件(如第3题)；三是不注意应用基本不等式的取等号的条件或不宜应用基本不等式的题型(如第4题).

对于后3题，看上去象一个题目，其实不然，它们的函数解析式尽管一样，但定义域不同，自然不是同一函数，求函数最值时，需要根据具体情况，采取不同的处理方法.

第2题不能直接应用基本不等式，需要将解析式变形，创造应用基本不等式的条件.

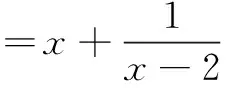
第3题也不能直接利用基本不等式，要先变形，创造运用基本不等式的正数条件.

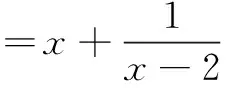
≤-2+2=0，

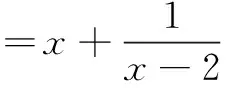
令x-2=t，则t≥2，

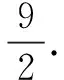
应用基本不等式求最值时,要把握基本不等式成立的三个条件“一正二定三相等”,忽略了任何一个条件,就会导致解题错误,因此熟练掌握基本不等式的使用条件和适用范围是至关重要的．

设计意图在突出基础知识的前提下,还要尽可能地多采用不同难度的同一题型,加强适应性训练,集中指向数学学科的核心素养.这样容易发现学生各种错误，就能真正让学生掌握这一知识点,让学生注意到其中的每一个细微差别之处,而不是死记硬背,生搬硬套.这也是数学学科核心素养所要求的数学能力.

二、对同一个题目的两种不同解法的研判

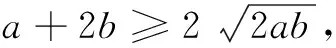
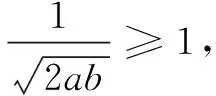
解法2因为a>0,b>0且a+2b=2，

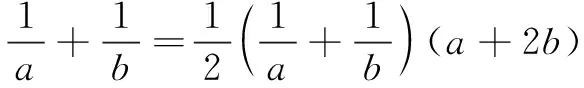
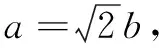
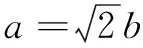
三、练习巩固

1.下列函数中,y的最小值为4的是 ( )

(Cy=ex+4e-x

2.下列结论正确的是 ( )