3D均值中值滤波参数对3D有序子集期望最大化重建图像的影响

甄琰明，张金铭，曲桂红，袁 波，赵书俊

[1.郑州大学物理学院(微电子学院)，河南 郑州 450001；2.北京大基康明医疗设备有限公司，北京 100176]

PET是核医学领域中比较先进的成像技术，其图像重建算法可分为解析法和迭代法。针对不同算法对PET图像质量的影响已有较多研究[1]。滤波反投影(filter back projection， FBP)算法[2]重建图像伪影较多，相比有序子集期望最大化(ordered subsets expectation maximization，OSEM)算法图像质量较差[3-4]。临床PET图像重建多采用OSEM算法[5]。由于放射性药物低剂量和欠采样等原因，采集到的投影数据(正弦图)经常被噪声严重污染而影响重建图像质量[6]。为提高重建图像质量，可在图像重建后、正弦图中或基于迭代统计的重建过程中进行噪声平滑。在正弦图中进行滤波处理计算效率高，无需过多修改已有机器配置，并能在重建图像中产生均匀的各向同性采样分辨率。MOKRI等[7-8]提出3D均值中值滤波器能有效去除噪声，并保持图像的边缘，但并未讨论滤波参数选择及不同滤波参数对重建图像的影响。本研究根据投影数据梯度分布直方图确定滤波参数的选取范围，从中等间隔地均匀选取一组滤波参数，对投影数据进行3D均值中值滤波，利用开源断层图像重建(software for tomographic image reconstruction， STIR)软件[9-10]中的3D OSEM算法重建滤波后投影数据，以视觉和定量方法评估滤波参数对3D OSEM重建图像的影响。

1 原理与方法

1.1 仿真数据 采用ECAT 962 PET扫描仪，利用分析模拟软件(ASIM)[11]模拟维度为288(radial bins)×144(angular views)×239(slices)的3D PET模体数据[12]，并根据米歇尔图(Michelogram)对其进行组合排列[13]，对包括600万真实符合事件、600万随机符合事件和210万散射符合事件在内的数据进行过衰减校正和轴向归一化校正。

1.2 3D OSEM算法 OSEM算法按投影角度将投影数据分成有限个有序子集，每个子集应用最大似然期望最大化(maximum likelihood expectation maximization， MLEM)[14]算法对图像更新一次,为一次子迭代,所有子集全部遍历为一次完整的迭代。相对MLEM算法,OSEM算法在一次迭代过程中重建图像更新n次，图像收敛速度加快[15-16]。OSEM的迭代公式如下：

(1)

式中yi表示第i条射线的投影数据，Hij表示第j号体素发出的光子被第i对探测器对探测到的概率，f表示待重建图像，k为该算法的迭代次数，Ts为第s个子集，s=1,2,...,n。

1.3 3D均值中值滤波算法[7-8]均值中值滤波器是基于最小化角度模糊伪影、平滑平坦区域及保持图像边缘3个目标设计的。定义3D正弦图为I(l,θ,z)，l是径向投影，θ是角度，z是切片。对正弦图的每个点定义一个梯度参数h(h∈[0,1])，根据高斯滤波后的正弦图的局部梯度信息得到该参数，计算公式如下：

(2)

F=(f2l+f2θ+f2z)1/2

(3)

式中fl、fθ和fz分别是高斯滤波后的正弦图在l、θ和z方向上的一阶导数。图像存在边缘时，一定有较大的梯度值；相反，图像比较平滑部分灰度值变化较小，则相应梯度也较小。h表示归一化后的梯度值，用于控制每个正弦图点上的平滑和增强水平，在平坦区域处应用较多平滑，在边缘区域处应用较少平滑。根据h值选取1个阈值Tm，将正弦图划分为2个区域进行分区域滤波[8]，见图1。

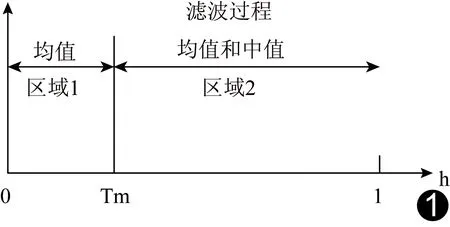
图1 区域1和区域2的划分

对区域1中的数据用2种不同尺寸模板计算均值，滤波后区域1中的所有数据值将替换为：

(4)

MeanA(l,θ,z)和MeanB(l,θ,z)分别表示整个3D数据用模板A和模板B完成均值滤波后的值。模板A比模板B具有更高平滑度。公式(4)表示平滑随h值增加而逐渐减少。h=0时，只采用模板A来施加大量平滑；h∈[0,Tm]之间，模板A的平滑程度通过结合模板B的贡献而减慢；h最接近Tm点处时，平滑程度则由模板B控制，即对较小h值施加大量平滑，对较大h值施加少量平滑，以去除噪声保持边缘。

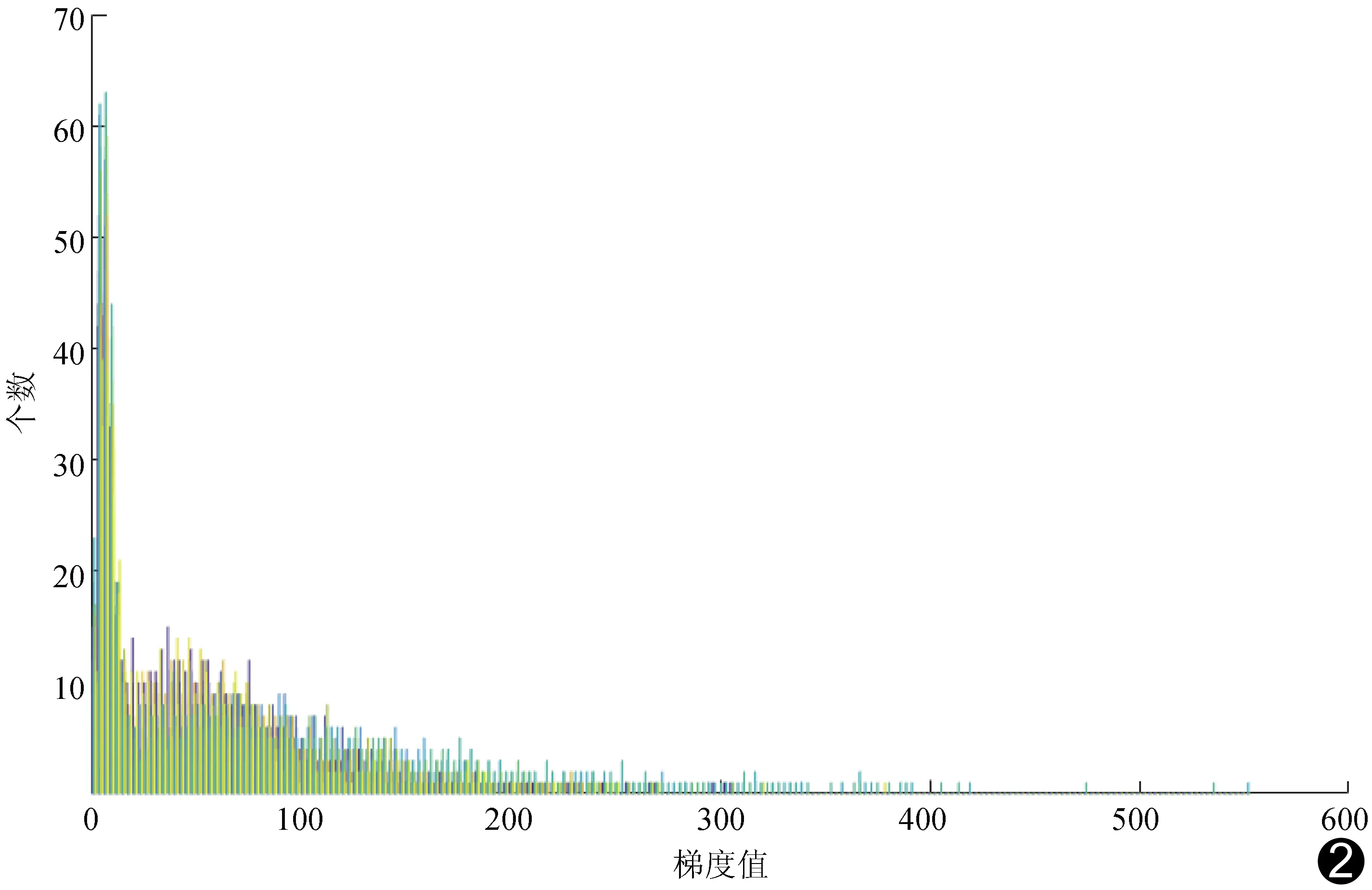
图2 梯度分布直方图

对区域2中数据采用角度分别为0°、15°、45°、75°、90°、105°、135°、165°的8个方向模板计算均值中值。方向模板表示正弦图中点的局部性，通过包括比角度分量更多的径向分量来减少重建图像中的角度模糊伪影。滤波后区域2中的所有数据值将替换为：

IRegion2(l,θ,z)=(1-h)×Meandir(l,θ,z)+h×Mediandir(l,θ,z)

(5)

均值Meandir(l,θ,z)和中值Mediandir(l,θ,z)的计算同理，中值计算公式如下:

(6)

ωi=ω1×ω2

(7)

mi是数组M的第i个方向模板Md的中值，为每个mi分配相应的权重ωi。如公式(8)计算权重ω1，σstd是标准差。如公式(9)计算权重ω2，dr是每组模板Md的平均值与中值的绝对差值，而σr是总计数值的平均值与中值的绝对差值。

(8)

(9)

对区域2中的滤波采用基于h值的加权策略，而不选择具有最佳权重的单个模板来估计均值Meandir(l,θ,z)和中值Mediandir(l,θ,z)，目的在于确保正弦图强度值随强度降低而逐渐平稳变化，避免正弦图中强度突然变化导致重建图像产生切向条纹，特别是在高强度区域和低强度区域之间的边界处。

2 结果

2.1 实验结果 用MATLAB画出正弦图梯度分布直方图(图2)，据以确定梯度控制参数K值的选择范围，从其中等间隔地均匀取K值分别为100、150、200、300、400、500、600。由公式(2)可知，参数h∈(0,1)，在0到1之间等间隔选取阈值Tm。分别用不同参数对数据进行均值中值滤波处理，得到数组数据。利用STIR中的3D OSEM算法对滤波前后3D正弦图数据进行重建，设置子集个数为9，迭代次数为12，得到数组实验结果。重建图像噪声及边缘保持效果对阈值Tm并不敏感，而对滤波参数K十分敏感；且实验结果符合MOKRI等[8]提出的高计数正弦图需要较低Tm值的结论，因此选取阈值较小的数组图像(图3～5)进行视觉评估,着重分析滤波参数K对重建图像质量和效果的影响。

参数K值过小时，图像边缘保持良好，但内部细节模糊；若参数K值过大，则边缘缺失，引起图像过光滑。不论如何选取K值，对比未滤波重建图像，滤波后重建图像中的噪声光圈消失，表明滤波后噪声减少，达到了去噪的目的。参数K值处于最大与最小中间的某个值时，既能有效抑制噪声，又可保持良好的图像边缘，且对比度有所提高。

2.2 定量分析 利用信噪比(signal noise ratio, SNR)、标准差(standard deviation, STD)和Brenner梯度函数定量评价仿真重建图像。图6中ROI局部SNR、局部STD计算结果见表1、2。K值≥300时，ROI的SNR一直小于未滤波数据重建图像SNR，若要保持良好图像边缘，则此区间范围的值不可取。滤波后重建图像ROI的STD恒小于未滤波数据重建图像ROI的STD，表明滤波后重建图像噪声减小，达到去噪目的。

局部SNR定义为ROI的局部均值与局部STD之比，如公式(10)所示。

(10)

Brenner梯度函数是最常用的计算图像清晰度的梯度函数[17]。正焦的清晰图像比模糊的离焦图像边缘更加锐利清晰，边缘像素灰度值变化大，因而梯度值更大，故可利用梯度函数获取图像灰度信息评判图像清晰度。基于Brenner梯度函数的图像清晰度定义如公式(11)所示。

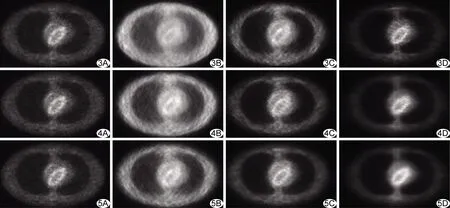
图3 采用3D OSEM重建滤波前后数据，原始数据重建图像(A)及固定Tm为0.1及滤波参数K分别为100、200、600的重建图像(B～D)图4 采用3D OSEM重建滤波前后数据，原始数据重建图像(A)及固定Tm为0.2及滤波参数K分别为100、200、600的重建图像(B～D) 图5 采用3D OSEM重建滤波前后数据，原始数据重建图像(A)及固定Tm为0.3及滤波参数K分别为100、200、600的重建图像(B～D)

表1 不同滤波参数边缘局部SNR和STD

注：未滤波数据重建图像的边缘局部SNR=3.63，局部STD=0.17

表2 不同滤波参数中央局部SNR和STD

注：未滤波数据重建图像的中央局部SNR=3.36，局部STD=0.81

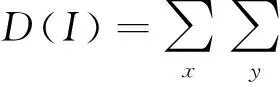
(11)

其中I(x,y)表示图像I对应像素点(x,y)的灰度值，D(I)为图像清晰度计算结果。

计算结果见表3。K值≥300时，滤波后数据重建图像的清晰度一直小于未滤波数据重建图像，提示处于此范围的值不可取。在考虑背景噪声减少和边缘信号保留及图像清晰度的情况下，综合图像视觉效果和定量分析结果，在梯度分布直方图区间100～300之间折中选取一个K值。本研究中，K值为150时实现了去除噪声保持边缘目的，可提供视觉清晰、高分辨率的图像。

不同数据的梯度分布直方图的梯度值范围不同。为使实验结果更具有参考价值，计算梯度分布直方图中K<150时的梯度分布占比为96.19%，作为参考标准。K<150时的梯度分布占比=K<150时的梯度计数值/K<600时的梯度计数值。对于不同数据，若求得梯度分布占比在96.19%左右，可自滤波参数范围中确定一个适当滤波参数进行折中，以获得视觉效果清晰的高质量图像。

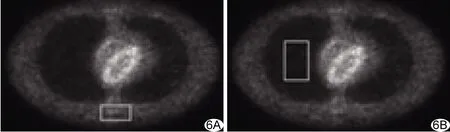
图6 ROI A.局部SNR； B.局部STD

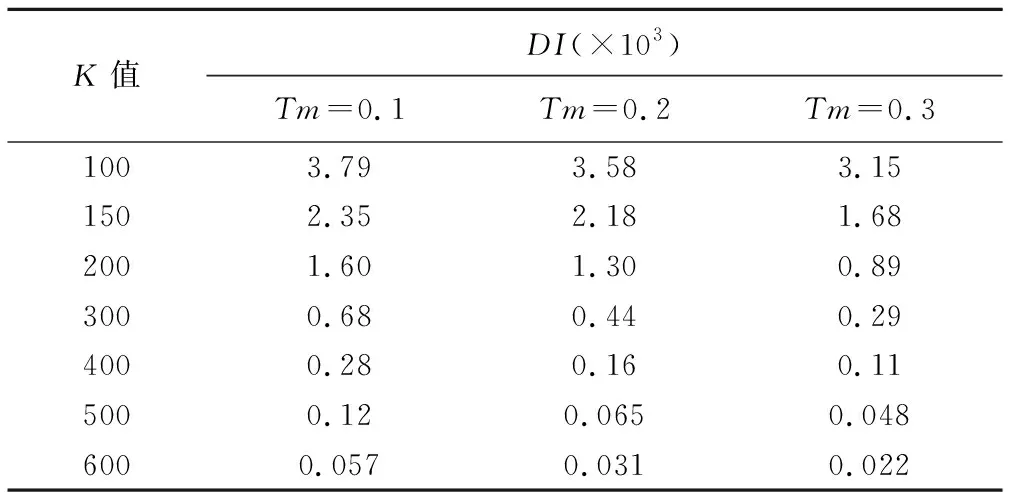
表3 不同滤波参数图像清晰度D(I)

注：未滤波数据重建图像的清晰度D(I)=1.36

3 讨论

PET可在病变区域内物理结构变化尚不明显的早期通过发现新陈代谢异常而加以确定，从而实现疾病早发现、早诊断及早治疗，提高治愈率。为临床诊断提供视觉清晰的高分辨率图像一直是重要研究方向之一。

本研究采用的均值中值滤波器的基本思想是根据不同h内容采取不同平滑方式，平滑强度(抑制噪声能力)在边缘区域减弱，在非边缘区域增强，从而抑制噪声，保护图像边缘。参数K值直接影响h中梯度信息的分布，梯度控制参数K直接决定均值中值滤波器的性能。

本研究结果表明，选取K值直接影响重建图像的噪声及边缘保持效果。图像中存在边缘部分时一定有较大梯度值，相反，图像中有比较平滑部分时，灰度值变化较小，相应梯度也较小。如所选K值过小，会将包含边缘信息的部分大梯度值划分到区域2，对区域2数据同时进行均值中值滤波可更好地保留边缘信号，但不能抑制图像中的所有噪声，尤其是具有大梯度值的噪声；相反，选取K值过大易将包含边缘信息的部分大梯度值划分到区域1，而区域1数据只接受均值滤波，虽可显著消除噪声，但会导致图像边缘缺失，使图像过度平滑。因此，K值最好是大于噪声产生的梯度并小于边缘产生的梯度。定量分析结果显示，滤波后数据重建图像的中央局部STD恒小于滤波前数据重建图像，可知不论如何选取K值，均可达到去噪目的。综合主观视觉效果和定量分析结果，可在区间100～300内确定一个最优K值。本研究在此区间内折中选取K值，从视觉效果和定量评估中获得视觉清晰、高分辨率的图像，并计算该值在梯度分布直方图中的梯度分布占比，将其作为一个参考标准。针对不同数据可依据此标准从滤波参数范围中确定适当的滤波参数，达到折中效果，获得视觉清晰的高质量图像。

本研究所涉方法及数据仅针对本机型，且仅初步分析不同滤波参数对3D OSEM重建图像的影响，并确定滤波参数的选取范围；今后将进一步寻求最优化算法来选取最优值。