基于热流固耦合的离心压缩机推力轴承温度场预测
2020-05-01侯秀丽孟继纲
侯秀丽,姚 洁,王 睿,孟继纲
(沈阳鼓风机集团股份有限公司,辽宁沈阳 110869)
1 引言
离心压缩机是石油炼化、合成氨、尿素、乙烯以及空气分离等行业的关键核心设备,其安全运行对企业有至关重要的作用。推力轴承是离心压缩机中承担残余轴向载荷的主要部件,其典型故障是由于机组载荷工况变化引起的油膜破裂、瓦温过高而导致的烧瓦、联锁停车等事故。目前,国内针对此类故障的研究侧重于故障排除和修复[1 -2],国外研究侧重于试验测试[3-4],对推力轴承的温度性能预测方面研究较少。辛争秋[5]采用流固耦合方法,借助CFX-Ansys研究了推力轴承润滑油膜温度分布,得出了推力轴承温度场。
本文基于热-流-固多场耦合分析,利用ROMAC-THRUST轴承分析软件,对某型号离心压缩机可倾瓦推力轴承的温度性能进行数值模拟研究,在考虑推力盘和瓦块的受力、受热形变的前提下,得到瓦块的温度分布云图,得出轴承瓦块最高温度与转速、进油温度、轴承载荷的关系,为推力轴承的设计、选型及故障诊断提供理论依据。
2 热流固耦合理论分析模型
在推力轴承实际工作中,油膜厚度与推力盘、瓦块的变形、油膜内压力分布相互影响[6]。同时,油膜在剪切力的作用下会产生热量,热量在轴承系统中的传递又会影响到推力盘和瓦块的形变[7],这是一个多物理场耦合过程,采用常规有限元软件计算较为复杂。
本文使用弗吉尼亚大学的专业推力轴承软件THRUST来进行推力轴承性能模拟,获取温度场。该软件可实现轴承瓦块、油膜和推力盘之间的热流固(TEHD)耦合,获得轴瓦温度分布云图或数据。涉及的主要理论模型有[8-9]。
2.1 雷诺方程
雷诺方程基于轴承的薄油膜特性,在瓦块平面内的坐标系上对Navier-Stokes方程进行了简化,并综合了连续方程。方程假设流体为牛顿流体,且瓦块、推力盘与油膜接触面无滑移。将边界条件带入后,得到方程
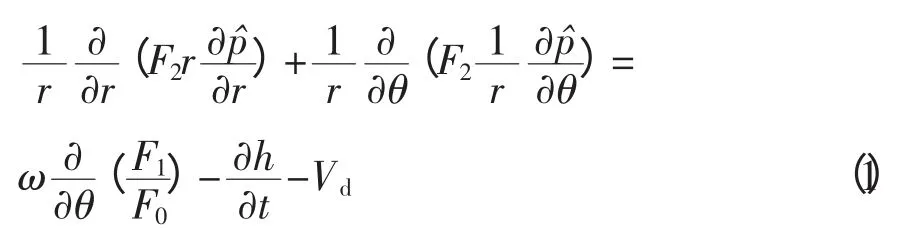
h——油膜厚度(通用定义)
(r,θ,z)——柱坐标分量
μ——流体粘度(通用定义)
Vd——边界流速
根据实际轴承运行状态,假设轴承为完全润滑。
2.2 能量方程
油膜能量方程也是以柱坐标形式给出的,其在方程中加入了两项,考虑了径向和周向的传热。
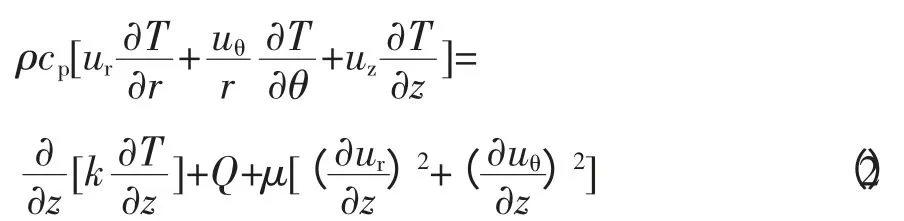
式中 ρ——润滑油密度
Cp——等压比热容
k——油膜导热系数
ur、uθ、uz——润滑油周向、径向、轴向速度分量
T——油膜温度
2.3 固体传热方程
稳态下推力盘和瓦块间的热传导会影响油膜的压力和温度,描述其传热的固体传热方程如下所示,其中关于推力盘轴对称热传导的假设已经被多人验证[10-11]

2.4 油膜厚度方程
为正确计算轴瓦表面的油膜厚度,其示意图简化如图1所示。其中(r,z,θ)为柱标系中各坐标分量。油膜厚度方程为

式中 hp——可倾瓦支点处的油膜厚度
Rc——支点半径
α/β——径向倾角、周向倾角
φc——支点夹角
αc、αr——周向倾角、径向倾角
χ——常数,一般取0.5
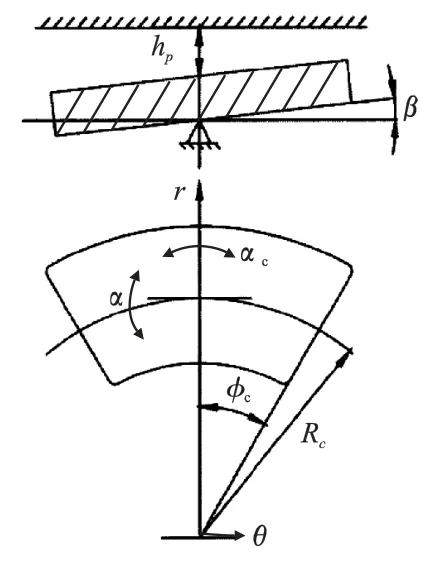
图1 轴瓦的油膜厚度示意图
2.5 润滑油粘-温-压方程
粘温模型采用Roelands粘度-温度-压力方程,其公式的表达式为
自发表以来,日本的井上红梅、佐藤春夫、竹内好、增田涉、高桥和巳、松枝茂夫等十多人纷纷翻译过《故乡》。使得该作品在日本广泛传播,至今仍被收录进日本的中学教材。本文选取了井上红梅译本和竹内好译本作为研究对象。

式中 T0——环境温度
μ0——环境压力和温度下的流体粘度
S0——热-粘参数
Z——压-粘参数
3 推力轴承温度场计算模型
本文以某型号离心压缩机推力轴承为研究对象,涉及的推力轴承、推力盘结构和材料特性、润滑油材料特性、载荷及边界条件如下所述。
3.1 推力轴承和推力盘结构和材料特性
推力轴承和推力盘的结构尺寸和材料性能参数分别见表1和表2。
3.2 润滑油参数
润滑油采用ISO VG46号透平油,其各项参数见表3。
3.3 载荷和边界条件
润滑油供油温度取35℃和45℃,转子转速范围5705~8705 r/min,支点油膜厚度0.1 mm,瓦块周向倾角0.05°。

表1 推力轴承和推力盘主要结构尺寸

表2 推力轴承和推力盘材料参数

表3 润滑油参数
4 推力轴承轴瓦温度场计算结果及分析
图中,左侧为瓦块的润滑油进口边,右侧为润滑油出口边,三张图的温度场分布规律一致,从图中可以看出:轴瓦进油边轴瓦温度最低,而出油边外径处轴瓦温度最高。这是因为润滑油从进入轴瓦面开始就承受剪切力,使得油膜温度不断上升,进油边有冷油不断补充,且不在核心承载区,温度较低,在出口外径处油膜最薄,承载较大,且散热不好,温度因此达到了峰值。
推力轴承瓦块最高温度是辨识轴承能否安全承载的直接参数。为了进一步明确转速、轴承载荷、供油温度对瓦块最高温度的影响规律,本文进行了多组计算对比分析。
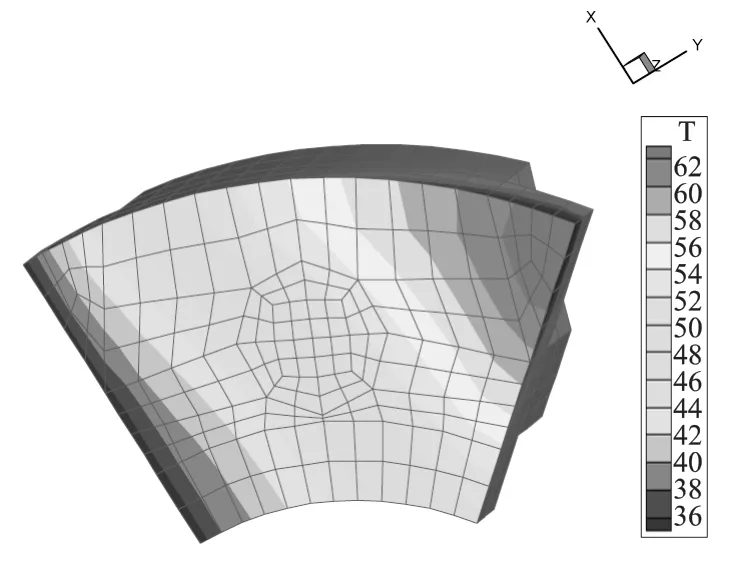
图2 轴瓦温度分布云图(转速5705 r/min)

图3 轴瓦温度分布云图(转速6705 r/min)

图4 轴瓦温度分布云图(转速7705 r/min)
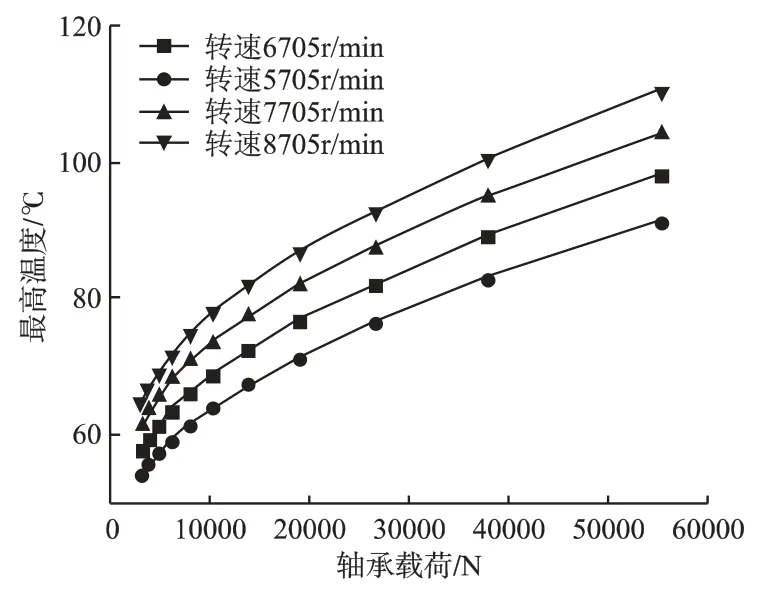
图5 不同转速下轴承载荷与最高温度关系曲线(Tin=35℃)
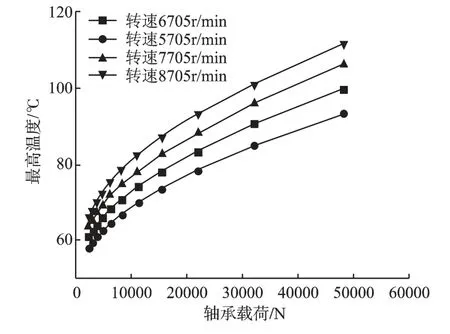
图6 不同转速下轴承载荷与最高温度关系曲线(Tin=45℃)
图5和图6为不同转速、不同供油温度下的轴向载荷和最高温度的分布曲线。图中可以看出:
(1)相同的供油温度和载荷下,轴瓦最高温度随转速升高而升高。这是由于油膜厚度方向的速度梯度随转速升高而增大,油膜中能量损耗加大。
(2)相同的供油温度和转速下,轴瓦最高温度随着载荷的增加而升高。这是由于油膜随载荷的增大会被挤压变薄,油膜的速度梯度增大,产热增加,通过热传递给瓦块,导致轴瓦温度上升。但轴瓦温升的趋势逐渐变缓,原因主要在于油膜厚度随轴向力增大减薄的越来越慢,最后趋于稳定,因此剪切力梯度也逐渐变小,摩擦产热速率降低。
(3)相同的转速和轴向载荷下,轴瓦的最高温度随供油温度升高而升高。提高供油温度后,与轴瓦接触的整体润滑油温度升高,轴瓦的最高温度也随之上升高。
5 结论
本文介绍了基于热流固耦合的推力轴承温度场预测,采用THRUST软件计算得出了某压缩机用推力轴承温度场分布,得到了最高瓦温随转速、载荷和供油温度的变化规律,得出如下结论,为压缩机用可倾瓦推力轴承的设计、选型和故障排除提供了理论支撑:
(1)相同供油温度、相同载荷下,转速越高,轴瓦最高温度越高;
(2)相同供油温度、相同转速下,载荷越大,轴瓦最高温度越高;但轴瓦温度升高的趋势逐渐变缓;
(3)相同转速,相同轴向力时,供油温度越高,轴瓦的最高温度越高。
