例析数形结合思想在高中物理解题中的应用

■韩 冰

数、形是高中物理解题中十分重要的元素,两者虽然在表现形式上有所不同,但是却存在十分紧密的内在联系。通过代数运算来解决复杂的物理问题,可以让解题过程更加精炼,而图形也能让问题描述变得更加直观。同学们在解决物理问题时,要培养数形结合思想,做到数、形互补,以便更加准确地解决物理问题。

一、以数助形,解决物理问题

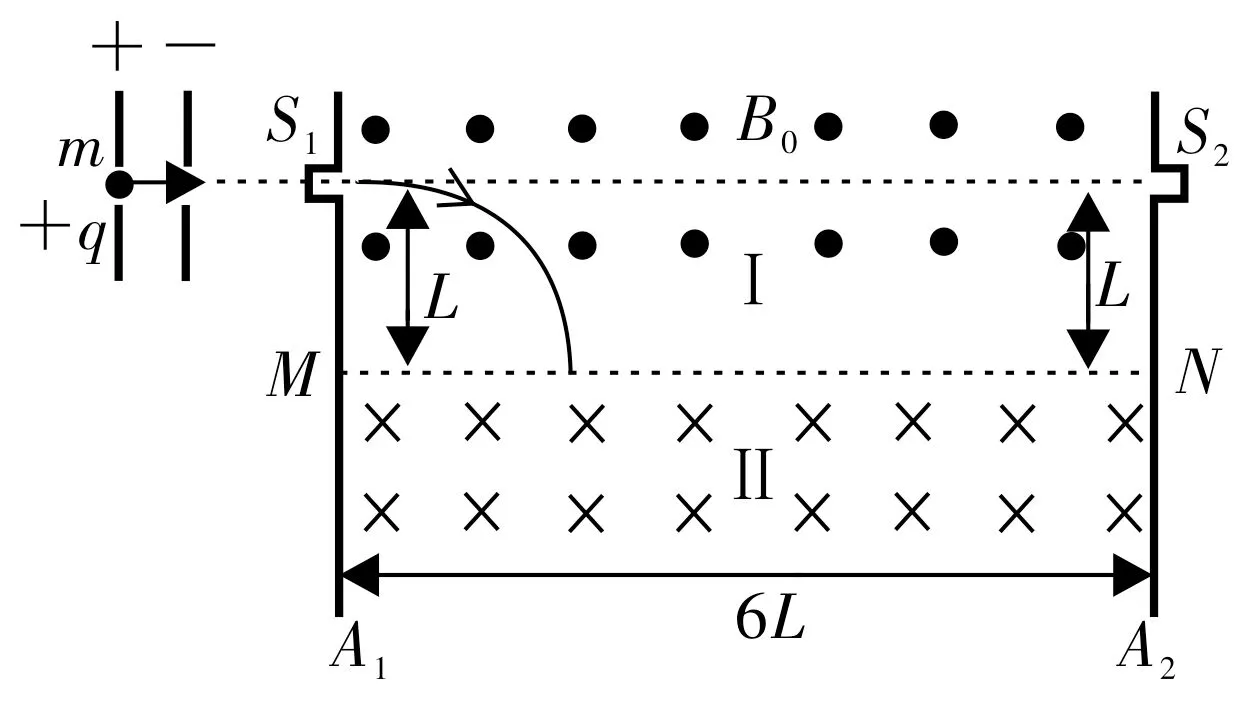
图1

例1 如图1所示,两个平板A1、A2的厚度、大小一模一样,现将A1、A2两个平板与地面成垂直状态放置,且两平板间的距离是6L。A1、A2两平板间存在匀强磁场Ⅰ、Ⅱ,两磁场的方向相反,MN是两磁场的分界线。在A1、A2两平板上存在两个小孔S1、S2,两个小孔处于同一水平面上,小孔S1、S2距离两磁场分界线MN的距离都是L,已知磁场Ⅰ的磁感应强度是B0。假设有一个粒子在匀场电场中,从静止开始加速,沿水平方向通过小孔S1进入磁场Ⅰ,经过磁场分界线MN上的P点,进入磁场Ⅱ。已知匀强电场的宽度为d,粒子的质量为m,电荷量为+q,平板A1与P点间的距离是kL,试求：

(1)当k=1时,电场强度是多少?

(2)当2＜k＜3时,粒子通过P点进入磁场Ⅱ,做相应运动后再次回到磁场Ⅰ,随后沿着水平方向,从小孔S2出来。粒子在磁场运动中,速度v与k之间的关系是什么? 分析磁场Ⅱ的磁感应强度B与k的关系。

解析：(1)由功能关系得,粒子在磁场Ⅰ中运动,向心力由洛伦兹力提供,故。当k=1 时,R=L,解得E=。

(2)当2＜k＜3 时,粒子沿水平方向从S2口出来,因此粒子进入磁场Ⅱ后只发生一次偏转就回到磁场Ⅰ,则(R-L)2+(kL)2=R2,解得。粒子在磁场Ⅱ中运动时,向心力也是由洛伦兹力提供的,则,从几何关系和对称性得,解得,最终求出。

二、数形结合,突破重点

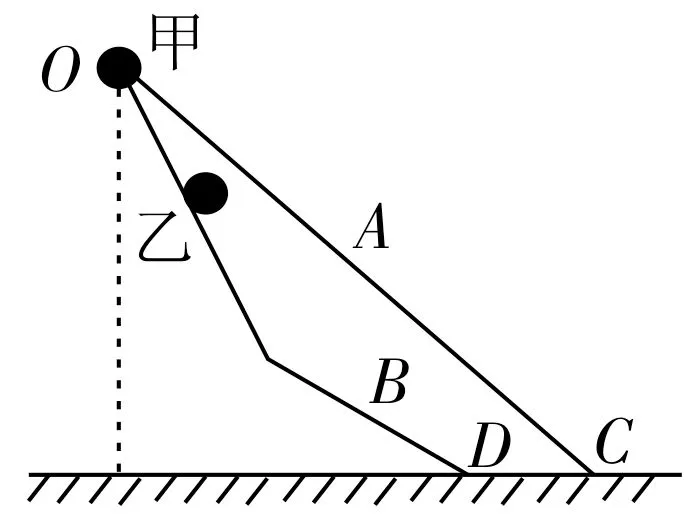
图2

例2有两个高度均为H且光滑的斜面,如图2所示,两斜面OBD与OC的总长度均为L,其中OC是一个斜面,OBD由OB、BD两个斜面构成。两个完全一样的小球甲、乙,从斜面上的O点出发,甲小球经OC斜面滑下,乙小球经OBD斜面滑下,忽视拐角位置能量损失,问：甲、乙哪个小球先到达地面?

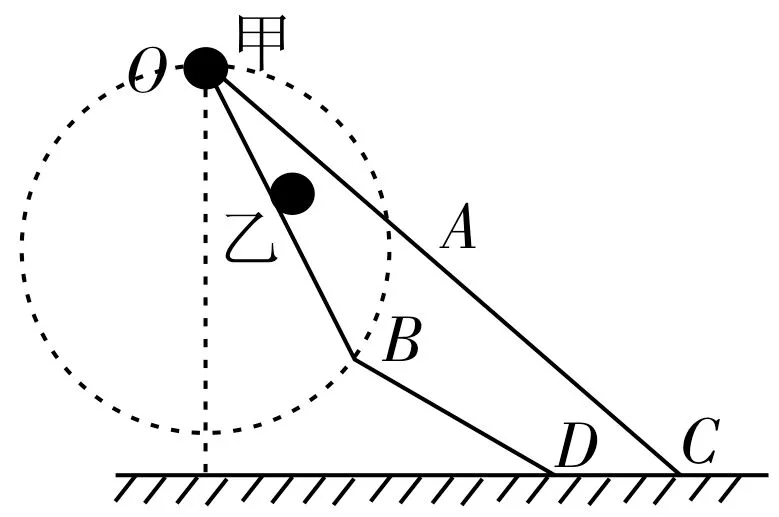
图3

解析：同学们如果单纯地进行计算,会感觉十分复杂,同时在计算过程中还容易出错。若建立相应的等时圆模型,求解过程将变得简单易懂。如图3所示,等时圆与OC的交点是A,与OB的交点是B,由等时圆模型可知tOB=tOA,由机械能守恒定律得vB＞vA,vC=vD。已知OC、OBD两个斜面的长度均为L,故xBD＜xAC,根据得tBD＜tAC,因此t乙＜t甲,即乙球会先到达地面。

总之,数形结合思想是一种十分有效的解题思维,将其应用到高中物理解题中,可以让同学们更加灵活、多变地处理物理问题,有助于同学们解题效率的提升。