浅谈带电粒子在磁场中运动的多解问题

■孙彦泽

带电粒子进入磁场后在洛伦兹力的作用下运动时,由于受种种因素的影响,常常会出现多解的情况。下面分三种情况结合例题进行分析。

一、平行直线边界的磁场

常见的临界情景和几何关系如图1所示。

图1

例1 如图2甲所示,间距为d、垂直于纸面的两平行板P、Q间存在匀强磁场。取垂直于纸面向里为磁场的正方向,磁感应强度随时间的变化规律如图2乙所示。t=0时刻,一质量为m、带电荷量为+q的粒子(不计重力),以初速度v0由Q板左端靠近板面的位置,沿垂直于磁场且平行于板面的方向射入磁场。当B0和TB取某些特定值时,可使t=0时刻入射的粒子经Δt时间恰能垂直打在P板上(不考虑粒子反弹)。上述m、q、d、v0为已知量。若,为使粒子仍能垂直打在P板上,求T0。

图2

解析：设粒子在磁场中做圆周运动的半径为R,周期为T,由圆周运动公式得T=。由牛顿第二定律得,将代入得d=4R。

若粒子的运动轨迹如图3所示,O1、O2为圆心,O1O2的连线与水平方向间的夹角为θ,在每个T0内,粒子只有在A、B两个位置才有可能垂直击中P板,且,由题意可知。设经历完整T0的个数为n(n=0,1,2,3,…)。若粒子在A点击中P板,则R+2(R+Rsinθ)n=d。当n=0时,无解；当n=1时,得；当n≥2时,不满足0＜θ＜90°的要求。若粒子在B点击中P板,则R+2Rsinθ+2(R+Rsinθ)n=d。当n=0 时,无解；当n=1时,得；当n≥2时,不满足0＜θ＜90°的要求。

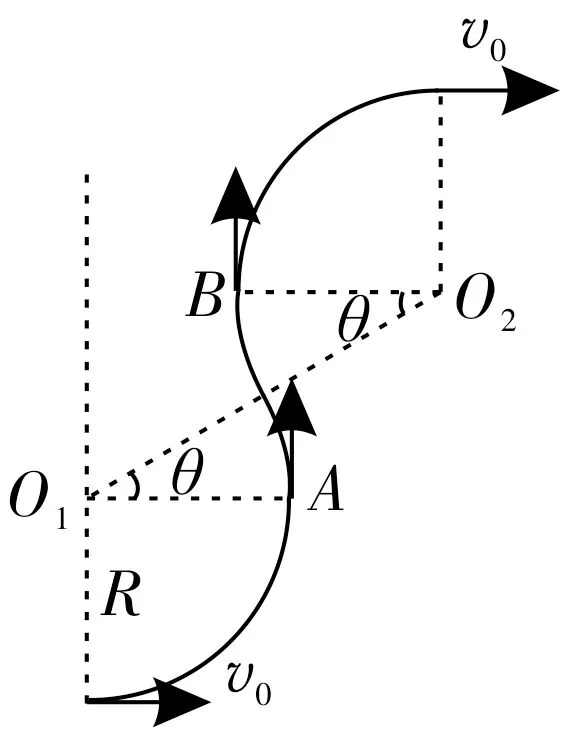
图3

图4

二、直线边界的磁场

如图5所示,粒子进出磁场具有对称性。当粒子进入磁场时的速度垂直于边界时,出射点距离入射点最远,且dmax=2R,如图5甲所示；同一出射点,可能对应粒子的两个入射方向,粒子在磁场中的运动轨迹一个是“优弧”,一个是“劣弧”,如图5乙、丙所示。

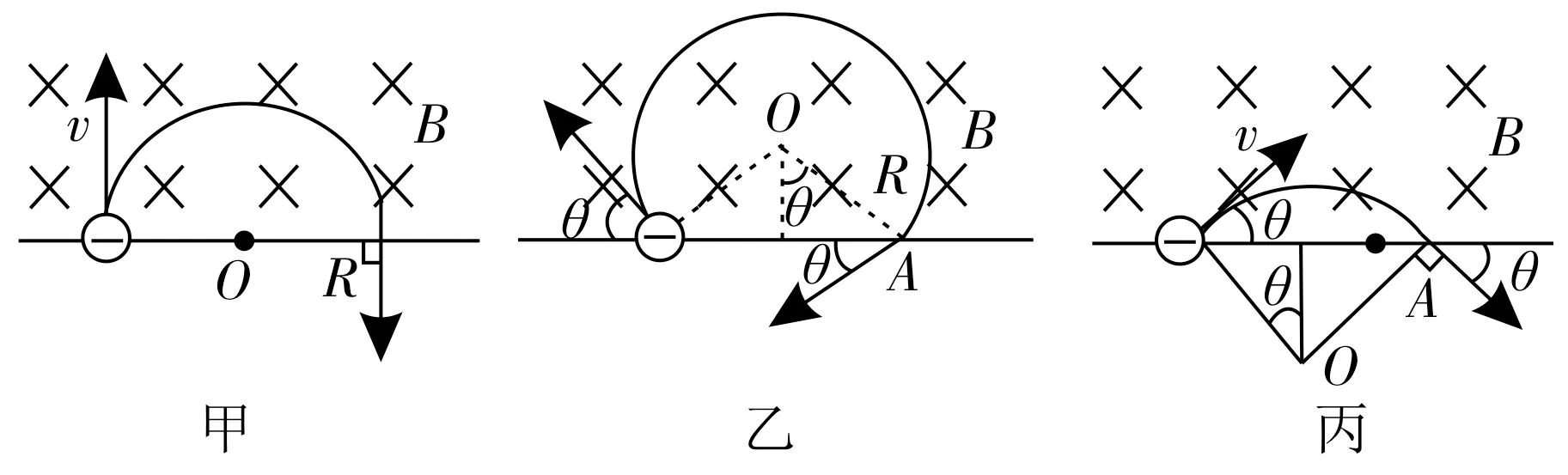
图5

例2 如图6甲所示,空间存在着两个方向均垂直于纸面向外的匀强磁场区域Ⅰ和Ⅱ,磁感应强度大小分别为B1、B2,且B1=B0,B2=2B0,虚线MN为两个磁场的边界。一质量为m、电荷量为q的带正电粒子(不计重力)从边界上的A点以一定的初速度竖直向上射入匀强磁场区域Ⅰ中,边界MN上的C点与A点间的距离为d。试求该粒子从A点射入磁场的速度v0为多大时,粒子恰能经过C点。

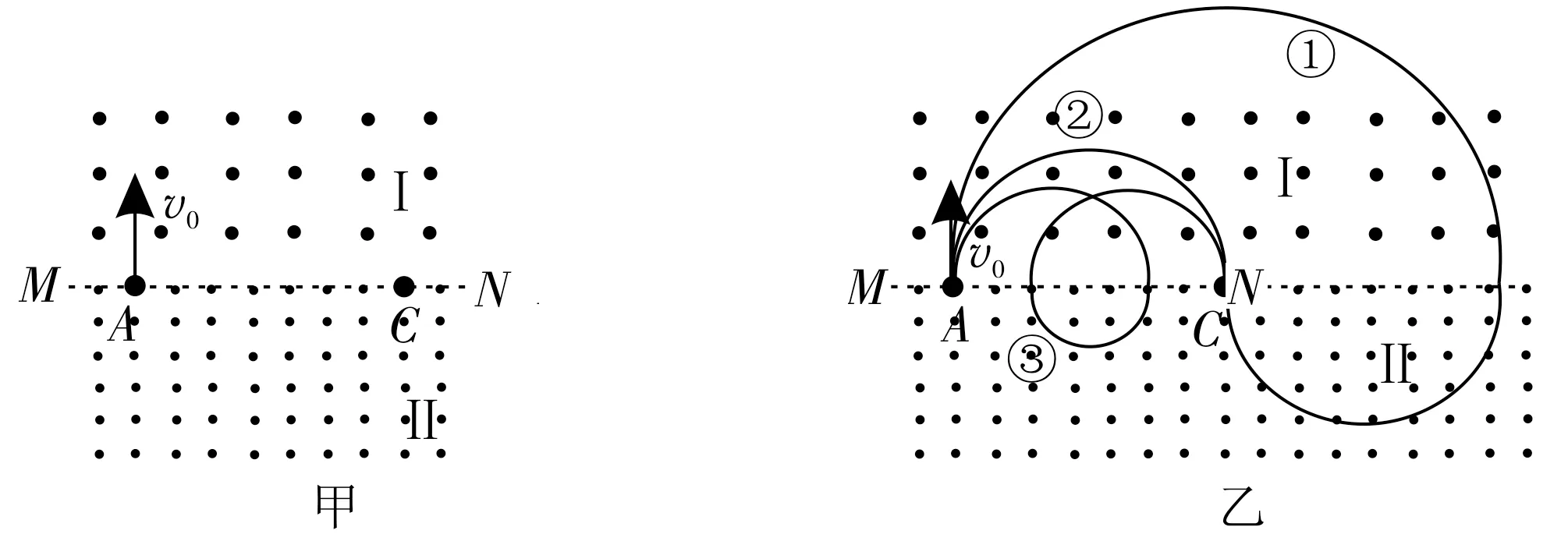
图6

解析：设粒子在磁场区域Ⅰ中做圆周运动的半径为r1,在磁场区域Ⅱ中做圆周运动的半径为r2,则,得r1=2r2。由题意知,速度v0的最大值对应的半径应为r1=d,如图6 乙中①所示。若粒子在A点的速度小一些,则凡是做圆周运动的半径满足d=nr1(n=1,2,3,…)的粒子都能满足恰能通过C点的条件,如图6中②③所示,即,又有,解得。

三、圆形边界的磁场

图7

①若粒子沿着边界圆的某一半径方向进入磁场,则粒子离开磁场的速度的反向延长线一定过磁场区域的圆心(沿着另一半径方向射出),如 图7 甲 所 示。②若粒子射入磁场时的速度方向与入射点对应半径间的夹角为θ,则粒子射出磁场时的速度方向与出射点对应半径间的夹角也为θ,如图7乙所示。

例3一半径为R的薄圆筒处于磁感应强度大小为B的匀强磁场中,磁场方向与筒的中心轴线平行,筒的横截面如图8所示。图中直径MN的两端分别开有小孔,筒可绕其中心轴线转动,圆筒的转动方向和角速度大小可以通过控制装置改变。一不计重力的带负电粒子从小孔M沿着MN方向射入磁场,当筒以大小为ω0的角速度转过90°时,该粒子恰好从某一小孔飞出圆筒。若粒子速率不变,入射方向在该截面内且与MN方向成30°角,则要让粒子与圆筒无碰撞地离开圆筒,圆筒的角速度应为多大?

图8

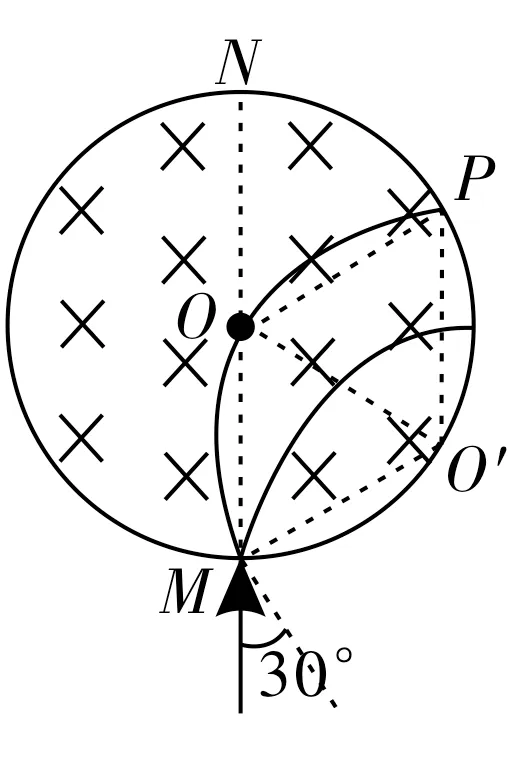
图9

解析：若粒子与MN方向成30°入射,速率不变,则半径仍为R,作粒子的运动轨迹如图9 所示,粒子的轨迹圆圆心为O′,则四边形MO′PO为菱形,可得,所以,则粒子在磁场中偏转的时间。又有,解得。因为圆筒的转动方向与射出孔不确定,所以需要分两种情况讨论。①当圆筒顺时针转动时,设筒转动的角速度为ω1。若粒子从N点离开,则筒转动时间,解得ω1=；若粒子从M点离开,则筒转动时间,解得。综上得ω1=。②当圆筒逆时针转动时,设筒转动的角速度为ω2。若粒子从M点离开,则筒转动时间,解得；若粒子从N点离开,则筒转动时间,解得。综上得)。