基于最小二乘法的室内三维定位算法研究

王桂杰，焦良葆，曹雪虹,

(1.南京邮电大学 通信与信息工程学院，江苏 南京 210003;2.南京工程学院 人工智能产业技术研究院，江苏 南京 211167)

0 引 言

近几年，随着智能电子设备在日常生活中的广泛应用，提供一套完整可靠的室内位置服务系统变得尤为必要。全球卫星定位系统(GPS)[1-2]作为一种发展成熟的室外定位技术，能够提供室外米级的定位精度。但由于室内环境因素的干扰，GPS信号被大大削弱，使其难以提供精确的室内定位服务。国内外专家学者对室内定位技术进行了大量研究，使得室内定位技术得到了快速的发展。

基于无线传感网络的室内定位技术包括红外线、蓝牙、WiFi、超声波、超宽带(UWB)等[3-4]。基于测距模型的定位系统提高定位精度的方式有如下两点：(1)选择最优的测距模型，尽可能克服室内环境的因素干扰，提高测距的精确度；(2)选择最优的定位算法对测距结果进行处理，求得最终的定位坐标。目前常用的室内测距模型包括如下几种[5-8]：接收信号强度(RSSI)测距模型、到达角度差(AOA)测距模型、到达时间/到达时间差(TOA/TDOA)测距模型等；常用的室内定位算法主要包括如下几种：三角质心定位算法、最小二乘定位算法、Chan氏定位算法[9]等。不同的定位算法都可以在一定精度范围内实现室内定位，也都存在一些需要被完善和解决的问题。

最小乘法是一种计算相对简单，便于实现的定位处理算法，但利用最小二乘法求解矩阵方程时要求系数矩阵应为非奇异矩阵，在具体的三维应用场景中即要求基站坐标选取时必须避免所有基站处在同一高度平面，即要求基站间在布局时必须存在一定的高度差值，且高度差值将直接影响标签高度坐标定位的精确度。首先介绍了到达时间(TDOA)测距模型和最小二乘法定位算法的原理并阐述了超宽带(UWB)[10-11]利用最小二乘法实现定位的具体方法，通过分析现实应用场景中传统最小二乘法所产生的定位误差及其产生的原因，提出了一种改进的最小二乘定位算法。该算法旨在降低最小二乘法对于基站三维几何布局的依赖关系，提高三维定位坐标的精确度。最后通过实验证明，该算法比传统最小二乘法定位算法在三维定位精度上有了明显的提升。

1 定位模型

1.1 基于UWB的TDOA测距模型

到达时间(TOA)方式利用标签发射信号到接收基站，通过到达基站时所用的时间求得信号发射点与接收点之间的距离。而TOA要求被测点与接收机保持严格的时间同步，多数应用场合无法满足这一要求。与TOA类似，TDOA只是测量得到时间差而非绝对时间[12]。这种方法只需接收基站之间保持同步，不要求与被测标签间时间同步，使系统相对简化，所以在定位系统中应用最广。

UWB是以相比较于传统统通信方式更宽的频谱进行通信的，其可以使用更少的电能，更快地进行数据传输，其脉冲宽度非常短，且在抗多径以及穿透性等诸多方面有着传统无线通信方式无法实现的优势[11]。TDOA模型通过UWB通信方式测量标签到每两个基站之间的距离差，距离差等于常量即可绘制出双曲线，而曲线交点即可确定标签坐标。该方法在实现过程中，标签只需要广播一次无线信号即可，因此有利于标签的功耗及标签并发数量。

1.2 最小二乘法

最小二乘法(least square method)是一种数学优化算法，又被称为最小平方法。它利用最小化误差的平方来寻找数据最佳匹配结果。通过最小二乘法求解未知变量的过程相对比较简便，且所求得的结果与实际数据之间误差的平方和为最小值。最小二乘法还可用于曲线拟合，以及其他优化类问题的求解[13-15]。

利用最小二乘法求解超限定方程组(未知数个数大于方程个数)十分方便，假设有m个等式，n个未知数x，m>n，则有方程组：

(1)

其中，i=1,2,…,m。将上式向量化得：

AX=B

(2)

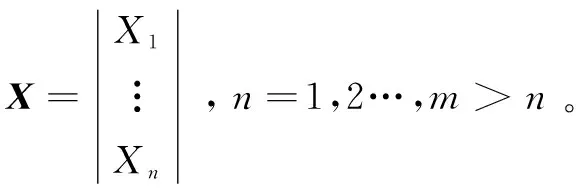
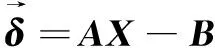
(3)

取误差向量δ无穷小时，X有最优解，令：

f=δ2=δTδ=(AX-B)T(AX-B)

(4)

对式(4)进行求导，并令其结果等于0，可得：

(5)

如果ATA为非奇异矩阵，则AX=B有唯一解，由下式可求解得：

X=(ATA)-1ATB

(6)

2 基于UWB的最小二乘定位算法

假设三维空间中有n(n≥4)个固定基站节点，基站节点的坐标分别为(x1,y1,z1),(x2,y2,z2)，…，(xn,yn,zn)，设待求的移动标签节点坐标为p(xp,yp,zp)，标签节点与基站节点之间的距离为d1,d2,…,dn。为保证最小二乘法在求解矩阵方程时，系数矩阵满足非奇异的要求，按照相邻基站不在同一水平高度的分布原则进行基站布局，如图1所示。

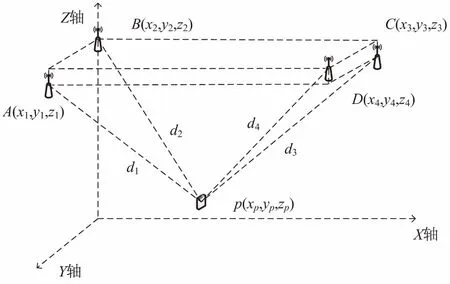
图1 室内基站分布于不同水平面

则有：

(7)

整理后得：

(8)

其中，kn=x2n+y2n+z2n，n=1,2…。

由相邻两式相减可得：

(9)

其中，xn(n-1)=xn-xn-1,yn(n-1)=yn-yn-1,zn(n-1)=zn-zn-1,kn(n-1)=kn-kn-1,n=2,3…。

令：

(10)

(11)

(12)

将式(10)～(12)带入式(6)求解矩阵方程，可得移动标签节点坐标p(xp,yp,zp)。

3 算法优化及实验分析

3.1 最小二乘法的定位优化

前面提到，为保证矩阵方程在求解时能够求得唯一解，系数矩阵应满足为非奇异矩阵的要求。在基站布局的时候就要求基站不能处在同一高度平面，基站间的水平高度差值如果太小会对最终标签Z轴的定位精度产生很大的干扰，所以为保证三维坐标的精确度，可以通过优化基站的几何分布，来提高标签垂直方向上的定位精度。但在实际的室内环境下，受室内高度限制，最小二乘法定位算法将无法满足三维定位精度的要求。为了降低最小二乘法对于基站几何布局的依赖性，基于最小二乘定位算法，选择由二维到三维分步求解的方式来实现三维坐标的定位。

在不考虑基站水平高度差对定位精度带来的影响的情况下，为保证系数矩阵不为奇异矩阵的同时，基站的水平高度差值可取得相对小一点，将基站布置在近似相同的水平高度上，如图2所示。

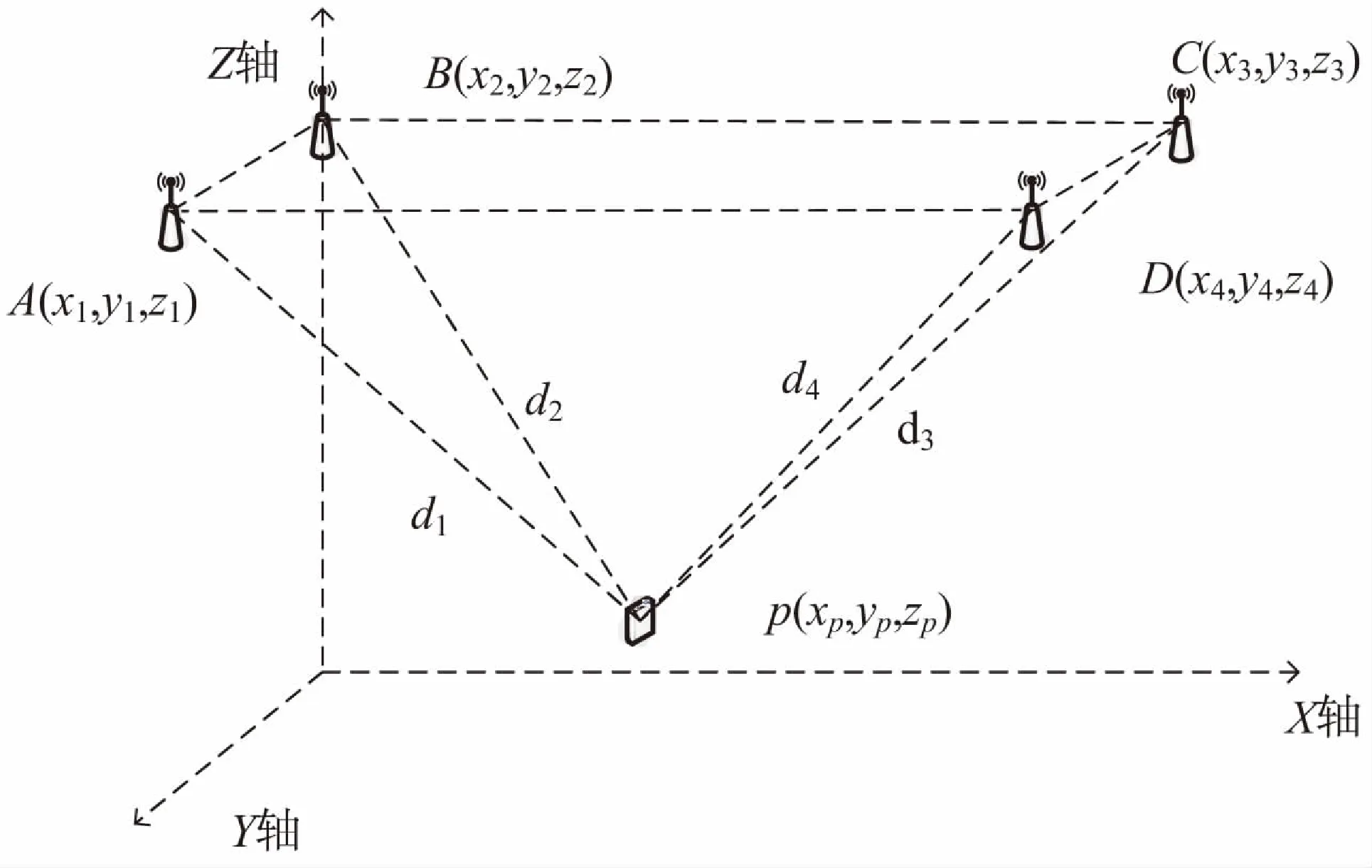
图2 室内基站分布

已知基站A、B、C、D的坐标分别为(x1,y1,z1)、(x2,y2,z2)、(x3,y3,z3)、(x4,y4,z4)，分别测得它们与标签p点(xp,yp,zp)之间的距离为d1、d2、d3、d4。根据最小二乘法可以求得标签p的二维坐标(xp,yp)，假设标签与不同基站之间的水平高度差值为Δhi,i=1,2…；则Δhi可由式(13)求得：

(13)

由式(14)可得标签的高度坐标hi：

hi=zi-Δhi

(14)

同理，可分别根据不同的基站坐标对标签高度进行求解，最后通过利用不同基站求得的标签高度取平均值，便可得到标签近似精确的三维坐标p(xp,yp,zp)：

(15)

3.2 实验分析

为验证优化算法的定位表现，选取12个标签将其均匀分布于15*6.5*4.5的室内环境中，标签坐标分别为(3.59,2.64,1.12),(2.74,3.98,0.87),(1.95,5.64,1.90),(7.87,2.43,2.35),(7.21,4.30,1.81),(8.17,5.86,1.50),(10.2,1.98,2.88),(11.02,3.53,2.56),(9.78,6.06,1.25),(12.77,2.59,0.56),(13.50,4.33,2.01),(14.66,6.18,3.14)。

室内设置4个基站节点，进行最小二乘法定位实验，基站坐标设置为(15,0,3.25),(0,0,4.5), (0,6.5,3.25),(15,6.5,4.5)，相邻基站间水平高度差值为1 m；利用最小二乘定位算法进行定位，每个标签进行1 000次的定位测试，表1为1 000次实验结果的平均值。

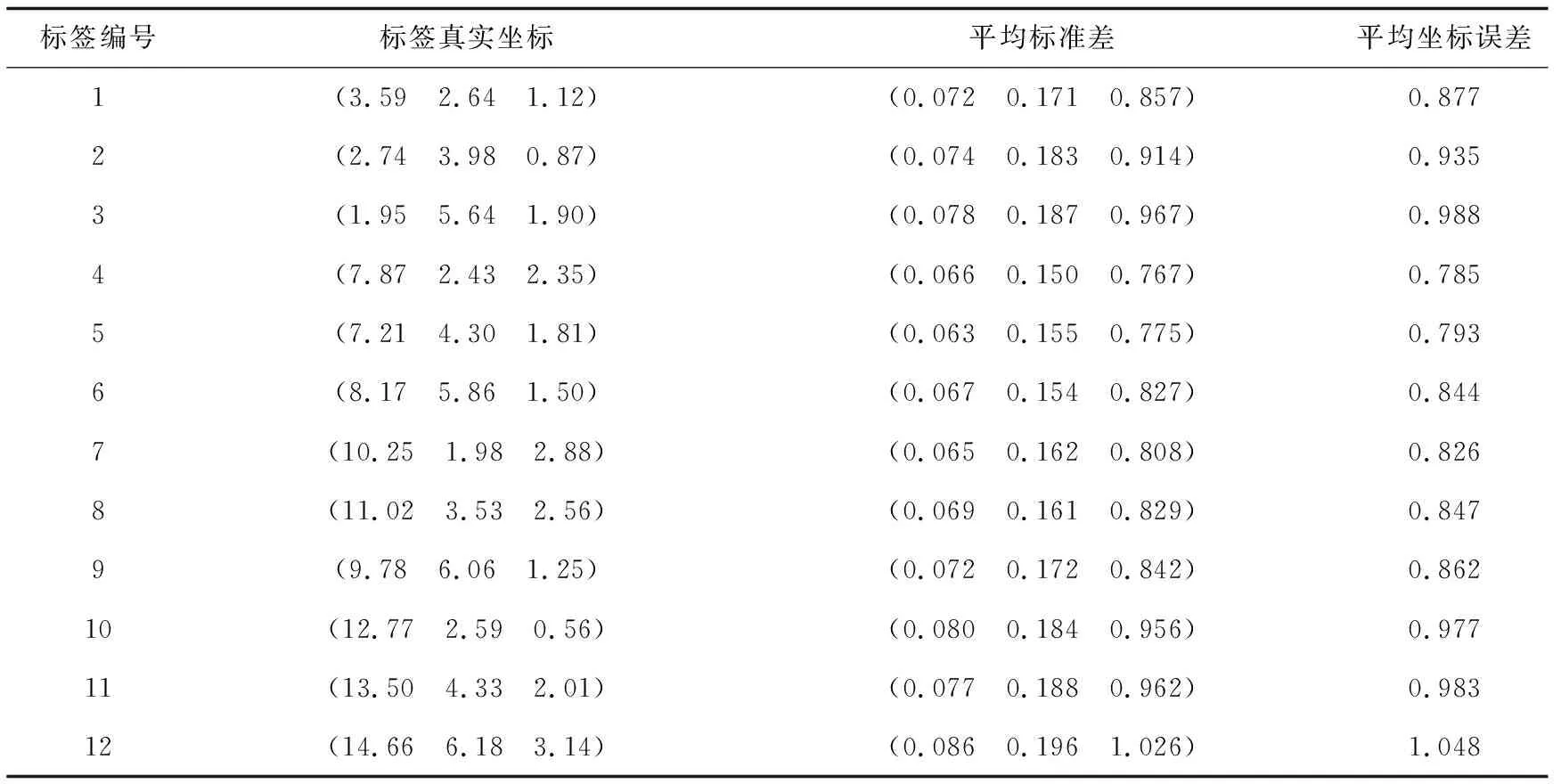
表1 最小二乘法定位算法实验结果 m

优化最小二乘法定位实验中，基站坐标设置为(15,0,4.25),(0,0,4.5),(0,6.5,4.25),(15,6.5,4.5)，相邻基站间水平高度差值为0.25 m；每个标签进行1 000次的定位测试，表2数值为1 000次实验结果的平均值。

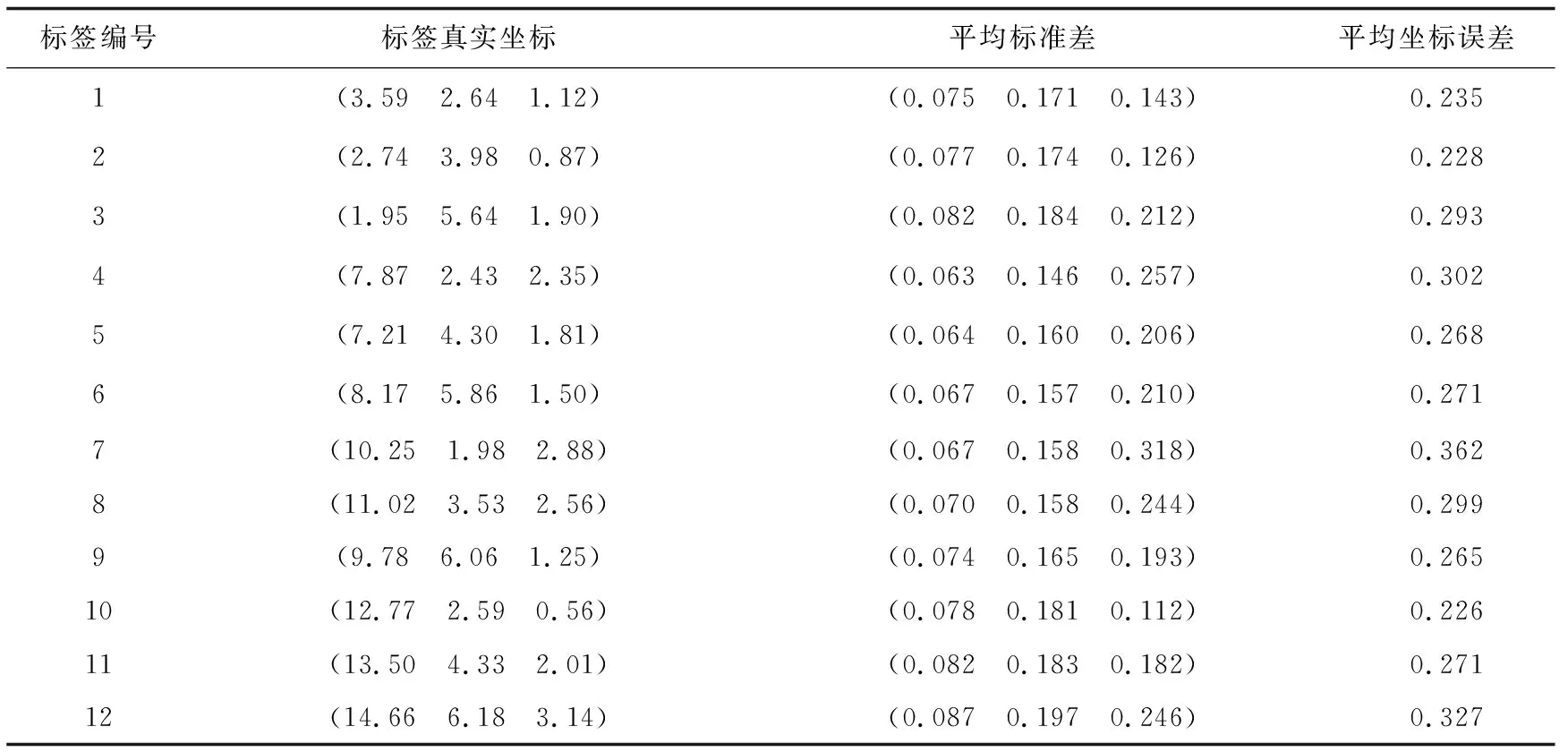
表2 优化的最小二乘定位算法实验结果 m

从表1和表2所得到的实验结果可知，最小二乘定位算法求得的坐标最小误差值为0.785 m，最大误差值为1.048 m，平均误差值为0.897 m；而文中提出的优化最小二乘定位算法的最小误差值为0.226 m，最大误差值为0.362 m，平均误差值为0.279 m。受基站水平高度差值影响，最小二乘定位算法在工作过程中定位误差波动比较大，定位效果不佳；相比于直接利用最小二乘法求解三维定位坐标，文中提出的优化最小二乘定位算法在定位精度提升68.90%，稳定性提升52.90%，两种算法的定位误差曲线如图3所示。可见优化后的定位算法定位误差明显要低，且误差曲线趋于平稳状态。

图3 误差曲线

4 结束语

文中提出的基于最小二乘法的定位优化处理算法在一定程度上解耦了室内三维坐标定位精度对于基站几何布局的依赖关系。通过构建实验模型，对算法进行实验分析，对比实验结果能够看出，优化后的最小二乘定位算法在定位精度方面性能提升了64.28%，稳定性方面性能提升了60.32%，由此证明该方法能够显著降低室内三维定位精度对于基站几何布局的依赖性，提高了三维坐标定位精度，定位效果明显优于未优化前的定位方法。