两种横向加速度计算方法对集装箱系固的影响
2020-04-30
(上海船舶研究设计院,上海 201203)
关于集装箱系固设计中的加速度计算,各方法的计算结果存在明显差异[1-3]。随着近年来理论计算方法和CFD技术的飞速发展,各船级社均致力于追求更精确和更经济的结果,持续地更新加速度计算方法。以中国船级社(CCS)规范为例,2009~2017年间共提出了3种集装箱系固加速度计算方法。其中最新的计算方法由CCS《钢质海船入级规范》2017修改通报(以下简称《CCS-2017》)提出。相对于此前由CCS《钢质海船入级规范》2012提出的计算方法(以下简称《CCS-2012》),《CCS-2017》采用了全新的封闭式计算体系,即不再提供具体的经验公式和计算流程,而代之以通过CCS船舶计算系统进行拟合确定。
《CCS-2012》向《CCS-2017》的转变被认为在大型集装箱船系固安全和效率之间取得了新的平衡[4],与德国劳氏船级社(GL)2013年规范中关于横向加速度计算方法的转变类似,与《GL-2007》相比,《GL-2013》得到的横向加速度明显偏低,甲板上集装箱最大堆重显著增加,堆重分布更加合理[5-6]。而关于CCS规范计算方法的转变对不同级别集装箱船系固设计的具体影响,目前未见报道。为此,拟通过具体算例对《CCS-2012》和《CCS-2017》进行对比,分析2种方法对不同级别集装箱船系固设计的影响,并进一步探讨《CCS-2017》中船型参数对横向加速度及最大堆重的影响。
1 两种横向加速度计算方法
考虑到甲板上集装箱对系固安全的要求更高,选择甲板上集装箱为研究对象。
《CCS-2012》中用于系固计算的横向加速度at为
(1)

(2)
式中:L为船长;x为计算点至尾垂线的距离。按式(1)计算得到的at值应不小于CCS规范结构强度直接计算方法中定义的合成横向加速度值。
《CCS-2017》规定的用于系固计算的横向加速度at为
at=(g+bv)·sinφm+bh·cosφm+
(3)
式中:g为重力加速度;bv为由纵摇和升沉引起的垂向运动的加速度;bh为由艏摇和横荡引起的横向运动的加速度;φm为船舶横摇角;TR为船舶横摇周期;z为集装箱重心位置距基线高度;zROLL为船舶横摇中心线距基线高度。bv、bh、φm及TR由CCS船舶计算系统根据船型参数进行计算。
从式(1)和式(3)可以看出,在其他条件一定的情况下,《CCS-2012》中的横向加速度仅与集装箱在船上的纵向位置有关,与垂向和横向位置无关;而在《CCS-2017》中,同一纵向位置的集装箱的横向加速度随z值增加而增大,这是更贴近实际情况的。
2 计算方案
2.1 不同船型对比计算方案
选取700、1 100、1 900、2 400及4 200 TEU 5型集装箱船为研究对象,在每型船的甲板上选取距艉垂线0.1L、0.3L、0.5L、0.7L和0.9L5个纵向位置。分别应用《CCS-2012》和《CCS-2017》对每一船型每一纵向位置上的20 ft和40 ft集装箱堆垛进行系固计算,得到100个用于计算的堆垛模型。主要船型参数见表1。

表1 研究对象的主要船型参数


图1 研究对象的系固布置方案
2.2 变船型参数计算方案
为探讨《CCS-2017》中船型参数对横向加速度及最大堆重的影响,选取4 200 TEU集装箱船为研究对象,选取方形系数Cb、最大服务航速V和船宽B这3个船型参数作为研究变量。其中,Cb的取值点为0.65、0.70、0.75、0.80;V的取值点为16、18、20、22 kn;B的取值点为32.2、34.8、37.3、40 m。上述船型参数的取值范围可覆盖本级别集装箱船中的巴拿马型、宽体型和内贸型3种典型船型。
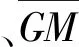
3 两种方法对不同船型的影响
3.1 横向加速度计算结果分析
采用《CCS-2012》和《CCS-2017》对2.1的计算方案展开计算,得到5型集装箱船的横向加速度at。定义堆垛高度中心位置的横向加速度为堆垛的平均横向加速度ata,用于反映堆垛整体的横向加速度水平。计算结果见表2。
表2的结果反映出《CCS-2012》中横向加速度与集装箱垂向位置无关、而《CCS-2017》中横向加速度随集装箱垂向位置增加而增大的总体特征,同时表明:
1)随着船舶尺度的增大,2种方法计算得到的横向加速度都呈现下降的趋势。这与文献[3]的结论是一致的。
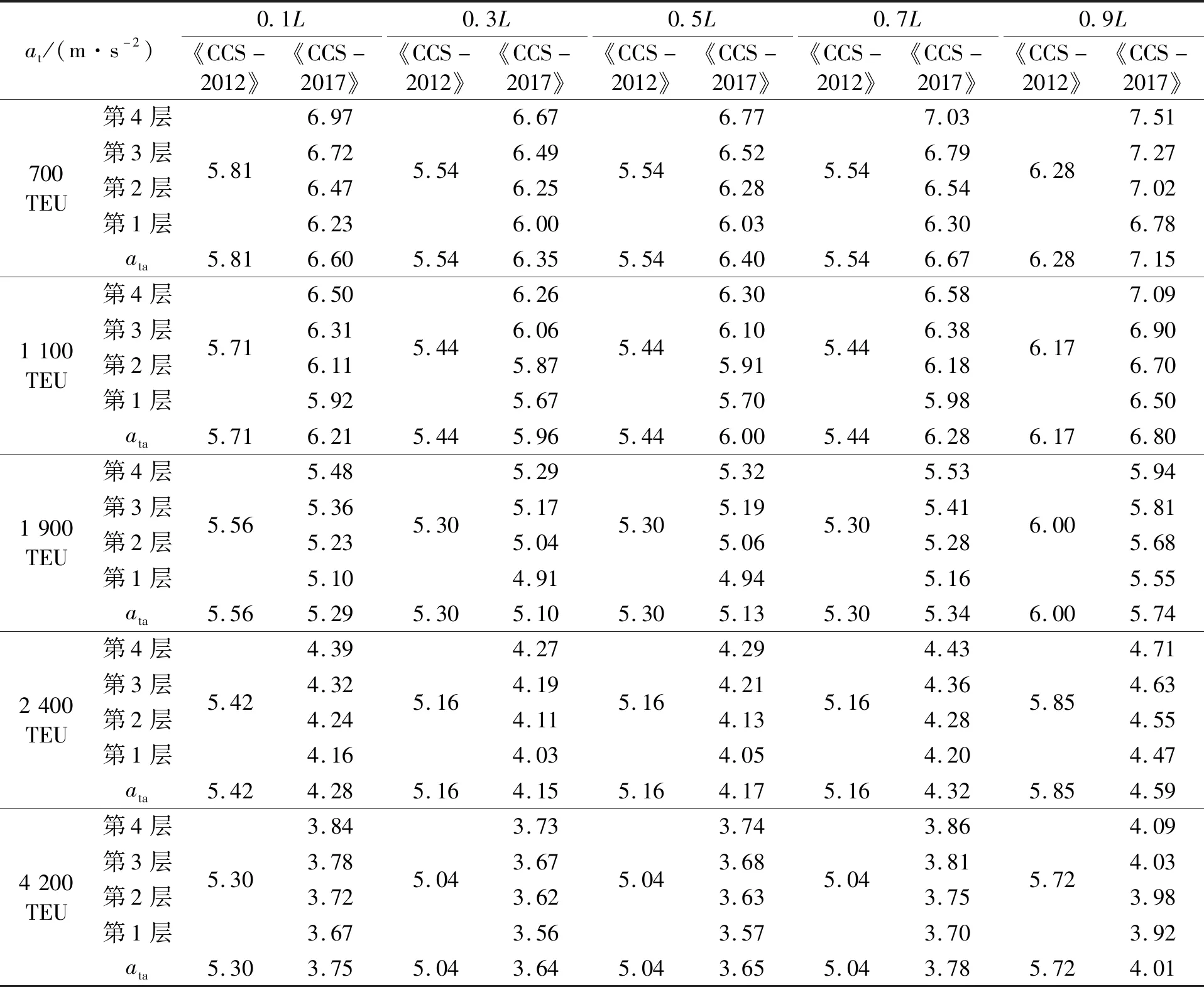
表2 横向加速度计算结果
2)纵向位置上《CCS-2017》计算得到的横向加速度最小值出现在距尾垂线0.3L位置附近,0.3L~0.9L范围内横向加速度递增。这与《CCS-2012》中横向加速度在距尾垂线0.2L~0.7L范围内保持恒定是不同的。
根据表2中的结果,对比同一船型不同纵向位置的平均横向加速度及不同型同一纵向位置的平均横向加速度发现:
1)2种方法对1 900 TEU集装箱船平均横向加速度的计算结果相差不大;对于700、1 100 TEU集装箱船,《CCS-2012》计算得到的平均横向加速度略低于《CCS-2017》;对于2 400、4 200 TEU集装箱船,《CCS-2017》计算得到的平均横向加速度显著低于《CCS-2012》。可见《CCS-2017》对船舶尺度大于1 900 TEU级的中、大型集装箱船的系固设计有利。
2)从表2中每层集装箱的横向加速度计算结果可知,对于700、1 100 TEU集装箱船,2种方法计算得到的横向加速度的差异随层数递增而增大,随船型增大而减小,《CCS-2017》计算得到的高层集装箱的横向加速度大幅高于《CCS-2012》。表明《CCS-2017》将为船舶尺度小于1 900 TEU级的小型集装箱船的系固设计带来一定的挑战。
3)《CCS-2017》计算得到的平均横向加速度随船舶尺度的增大快速下降,而《CCS-2012》计算得到的平均横向加速度随船舶尺度的增大仅小幅降低;对于2 400、4 200 TEU集装箱船,2种方法计算结果的差异随船舶尺度的增长呈扩大趋势。由此判断,对于船舶尺度大于1 900 TEU级的集装箱船,随着船舶尺度的增加,采用《CCS-2017》所获得的横向加速度相对于《CCS-2012》的降低幅度越大。
3.2 最大堆重计算结果分析
根据3.1的横向加速度计算结果对2.1的计算方案进行系固计算,得到5型集装箱船20 ft集装箱堆垛和40 ft集装箱堆垛的最大堆重SWmax计算结果,见表3。
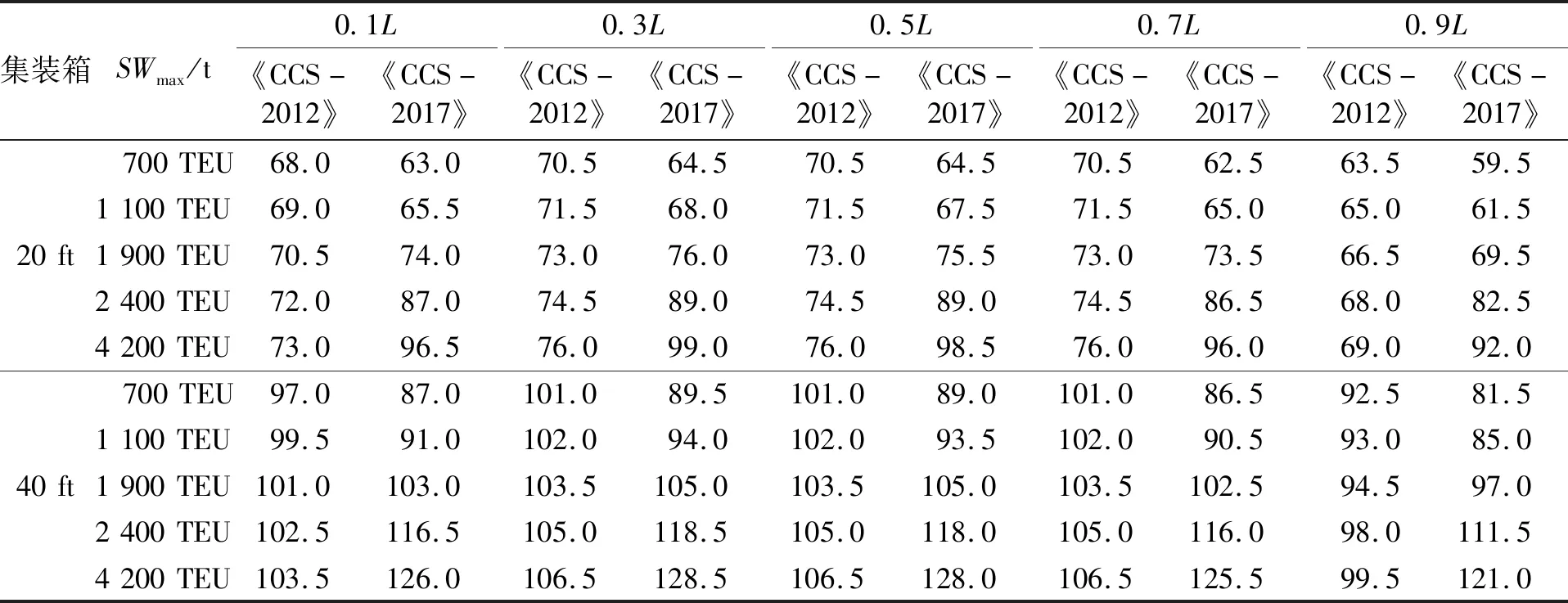
表3 20 ft集装箱堆垛最大堆重计算结果
分析表3的计算结果可知:
1)2种方法对1 900 TEU的最大堆重计算结果接近;对于700、1 100 TEU集装箱船,《CCS-2012》计算得到的最大堆重略高于《CCS-2017》;对于2 400、4 200 TEU集装箱船,《CCS-2017》计算得到的最大堆重显著高于《CCS-2012》。显而易见,采用《CCS-2017》有利于提高大中型集装箱船系固系统的堆重能力,这一点印证了文献4的观点;但小型集装箱船系固系统的堆重能力将因采用《CCS-2017》而受到一定损失。
2)《CCS-2017》计算得到的最大堆重随船舶尺度的增大快速增加,而《CCS-2012》计算得到的最大堆重随船舶尺度的增大仅小幅增加;对于2 400、4 200 TEU集装箱船,2种方法计算结果的差异随船舶尺度的增长呈扩大趋势。由此判断,对于船舶尺度大于1 900 TEU级的集装箱船,随着船舶尺度的增加,采用《CCS-2017》所获得的堆重优势越大。
4 船型参数对《CCS-2017》计算结果的影响
4.1 方形系数
根据2.2中的计算方案,针对Cb=0.65、0.70、0.75、0.80这4种情况,分别应用《CCS-2017》对分别位于距艉垂线0.1L、0.3L、0.5L、0.7L和0.9L共5个纵向位置的20 ft集装箱堆垛进行系固计算,结果见表4。

表4 不同方形系数情况下的ata和SWmax计算结果
表4表明,随着方形系数的增大,平均横向加速度呈下降趋势,最大堆重呈上升趋势。当方形系数由0.65增大到0.80时,距艉垂线0.1L~0.9L这5个纵向位置的平均横向加速度分别降低了9.9%、9.6%、9.7%、10.0%和10.5%,而最大堆重分别增加了8.9%、7.0%、8.7%、9.0%和9.5%。由此认为,方形系数增大对《CCS-2017》的计算结果存在较大的有利影响。
4.2 服务航速的影响
根据2.2中的计算方案,针对Vs=16、18、20、22 kn 4种情况,分别应用《CCS-2017》对分别位于距艉垂线0.1L、0.3L、0.5L、0.7L和0.9L这5个纵向位置的20 ft集装箱堆垛进行系固计算,计算结果见表5。
表5 不同航速情况下的ata和SWmax计算结果
表5表明,随着航速的增加,平均横向加速度呈微弱上升趋势,最大堆重呈微弱下降趋势。当航速由16 kn增大到22 kn时,距尾垂线0.1L~0.9L这5个纵向位置的平均横向加速度分别仅增加了2.2%、1.5%、1.6%、2.2%和3.4%,而最大堆重分别下降了1.6%、1.6%、1.1%、2.2%和2.9%。由此认为,航速增加对《CCS-2017》的计算结果存在微弱的负面影响。
4.3 船宽的影响
根据2.2中的计算方案,针对B=32.2、34.8、37.3、40.0 m 4种情况,分别应用《CCS-2017》对分别位于距艉垂线0.1L、0.3L、0.5L、0.7L和0.9L这5个纵向位置的20 ft集装箱堆垛进行系固计算,见表6。
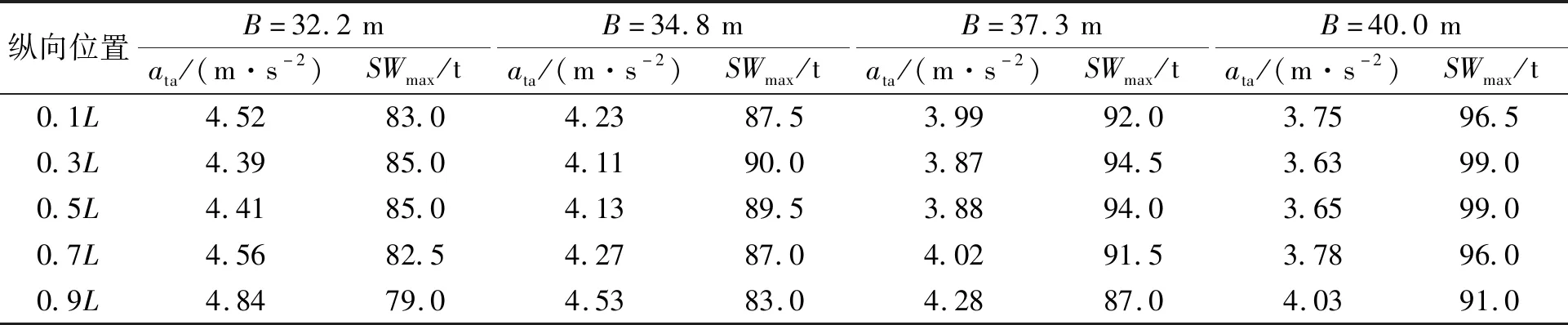
表6 不同船宽情况下的ata和SWmax计算结果
表6表明,随着船宽的增加,平均横向加速度呈下降趋势,最大堆重呈上升趋势。当船宽由32.2 m增大到40.0 m时,距尾垂线0.1L~0.9L这5个纵向位置的平均横向加速度分别仅下降了17.1%、17.1%、17.3%、17.1%和16.7%,而最大堆重分别增加了16.3%、16.5%、16.5%、16.4%和15.2%,变化幅度超过了式(1)所反映的《CCS-2012》中横向加速度与船宽的变化关系。由此认为,船宽增加对《CCS-2017》的计算结果存在较显著的有利影响。
对比上述方形系数和航速对计算结果的影响幅度可以认为,船宽是这3个船型参数中最主要的影响因素。
5 结论
1)与《CCS-2012》相比,《CCS-2017》对船舶尺度大于1 900 TEU级的集装箱船的系固设计有利;但将给船舶尺度小于1 900 TEU级的小型集装箱船的系固设计带来不利影响。
2)对于船舶尺度大于1 900 TEU级的集装箱船,随着船舶尺度的增加,《CCS-2017》对集装箱系固的优势越明显。
3)方形系数、航速、船宽对《CCS-2017》的横向加速度及最大堆重计算结果存在一定影响,其中船宽是最主要的影响因素。
计算结果显示,《CCS-2017》使4 200 TEU及以上的集装箱船获得超过90 t的无绑扎堆重(20 ft集装箱堆垛)、超过120 t的双层绑扎堆重(40 ft集装箱堆垛),使得20 ft集装箱堆垛不绑扎、40 ft集装箱堆垛两端无绑扎桥这一常规系固设计方案的潜力得以充分发挥,这对于优化中型集装箱船的总布置、提高经济性具有重要意义。
