基于改进KNN算法的动态手势识别研究

陈嘉伟，韩 晶，郝瑞玲，胡 迪

(1. 中北大学 机电工程学院，山西 太原 030051； 2. 中国人民解放军32382部队，北京 100072)

0 引 言

手势是最常用到的交流和操控方式，在日常生活中作用很大. 随着传感器技术的发展，手势识别成为了可能. 近年来，越来越多的研究者将微型传感器应用于人体动作的识别[1]，人们通过手势传感器获取手部动作数据，达到了人机交互的目的.

一直以来，手势识别的算法都是人们研究的重点. Mantyjarvi[2]提出了一种利用小波变换的计算机视觉人体动作识别的方法. 徐贤[3]等应用传统K最近邻(KNN: K-Nearest Neighbor)算法和电容式传感器实现了手势识别，相比普通的阈值识别方式，有效提高了识别成功率； 吕蕾[4]等利用数据手套实现了静态手势识别方法，通过静态手势特征以及相应的手势特征点集的提取来实现手势识别； 孙荣宗[5]等提出了一种基于粗糙集的KNN算法，将粗糙集与传统KNN算法结合，有效提高了KNN算法的识别效率. Xu Ruize[6]等通过定义多个手势信号的特征值并对其符号进行编码，结合Hopfield算法实现了手势识别. 本文结合上述研究，提出一种改进的KNN算法来对ADXL335传感器的手势动作识别，改进KNN算法对手势动作信号中提取的特征量进行编码，并将KNN算法的训练组数据进行了优化处理，从而提高手势识别结果的准确率，为了验证试验效果，本文在LabVIEW平台设计了一款体感俄罗斯方块[7]游戏.

1 算法原理

1.1 传统KNN算法

KNN算法[8]是目前常用的一种数据挖掘算法，广泛用于数据分析、 图像处理、 文本分类等领域[9-10]. KNN算法的基本思想是： 给定一个训练数据集，对新的输入实例，选定一个适当的距离机制，在训练数据集中找到与该实例最邻近的K个实例， 这K个实例的多数属于某个类，就把该输入实例分类到此类中.

KNN算法步骤：

1) 处理数据，对数据进行降噪处理；

2) 输入已分类的训练组向量以及测试组向量数据；

3) 根据距离机制计算训练组与测试组间的距离，多数采用欧式距离；

(1)

式中：Di,Dj分别为测试组向量与训练组向量；di,dj分别为测试组向量与训练组向量中的元素.

4) 根据计算出的距离大小，在训练组中选出K个与测试组数据Di距离最小的训练组数据，计算出测试组数据Di属于每个分类的权重Y，Di属于分类Xl的权重公式为

(2)

其中

(3)

5) 输出训练样本中权重最大的样本所属的分类标签.

传统KNN算法的不足[11]之处是当测试组分类不均衡时，会导致分类出的结果误差较大； 当传统KNN算法面对大样本数据集时，计算成本消耗较大.

1.2 改进KNN算法

在手势识别过程中，如果需要识别的手势数量较多，将会导致传统的KNN算法训练组数据过于庞大，从而影响识别效率. 改进KNN算法对手势识别中需要识别的手势进行特征提取，根据提取的特征值对手势进行编码，使得每个手势都有唯一的编码，这样有效减少了训练组的数据量，进而提高了手势识别的成功率. 目前，对于特征提取没有固定的规则，应用在动作识别中的特征主要有静态特征，动态特征以及时空特征[12]. 为了保证手势识别的准确，优化KNN算法中手势特征的选择应保证同类的特征量较为稳定且不同类的特征量的差异明显大于同类特征量[13]. 静态特征可以更好地反映出动作细节，因此本文对手势信号进行静态特征提取，加速度传感器采集到的信号为三维信号，可以将采集到的信号看作三维空间的向量从而方便特征提取，分别采集手势动作各轴向的幅值、 向量归一化值以及距原点的距离.

加速度传感器的信号经滤波器处理后较为稳定，记手背向上时的动作为初始动作，采集到的加速度信号为

GA=(xa,ya,za).

(4)

手掌右翻，左翻以及上抬时采集到的加速度信号为

Gi=(xi,yi,zi),i=1,2,3.

(5)

基于加速度传感器手势静态特征量提取的公式为

1)手势动作的幅值

GAGi=(ki,li,mi)=(xa-xi,ya-yi,za-zi),

i=1,2,3,

(6)

式中：k,l,m为做出手势动作后传感器产生的三轴信号的幅值.

2) 向量归一化

(7)

式中：Y代表输出的归一化向量；X代表长度为的向量.

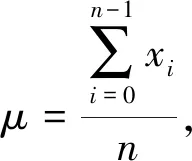
(8)

(9)

式中：xi是X的第i个元素.

3) 距原点距离差

(10)

根据改进KNN算法特征量提取方法，图1 手势信号所提出的特征量为

T1=(0.01,-0.18,0.16,1.32,-1.10,

-0.22,-1.25).

(11)

为了对提出的特征量进一步简化，分别检查提取特征量的符号，并将其储存为手势代码，若特征量的数值小于0.1，则将该特征量简化为0. 因此，图1 手势信号所提出的符号序列代码为

M1=(0,-1,1,1,-1,-1,-1).

(12)

改进KNN算法手势特征量的提取大大减少了数据量，从而降低了算法的复杂程度. 图1 手势信号的符号序列的提取如图2 所示.

图1 随机手势信号Fig.1 Random gesture signal

图2 随机手势信号特征量Fig.2 Characteristic quantities of random gesture signals

2 手势识别系统

2.1 手势操作俄罗斯方块

在LabVIEW平台搭建的手势操作俄罗斯方块系统中，利用ADXL335三轴加速度传感器实时采集动态手势信号，再通过美国国家仪器NI公司的USB-6002数据采集卡将信号输入LabVIEW程序中. 信号将在程序中经过二阶贝塞尔滤波器处理后，利用改进KNN算法对手势进行识别，从而对游戏进行手势操作. 系统框图如图3 所示.

图3 系统框图Fig.3 System block diagram

2.2 手势识别流程

手势识别实验流程如图4 所示. 在手势识别实验开始后，测试组数据将会以与训练组相同的方式进行手势特征量的提取.

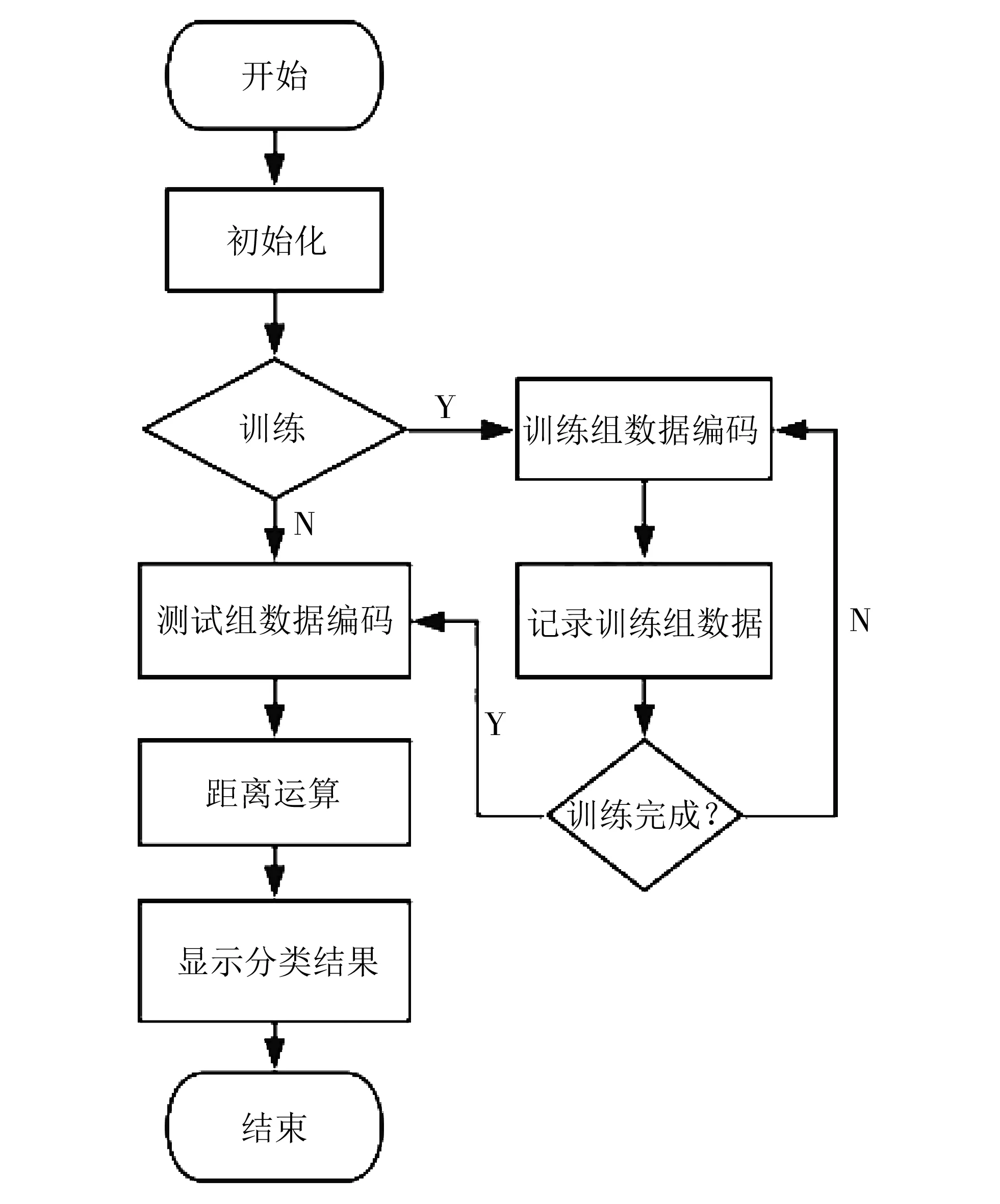
图4 手势识别实验流程Fig.4 Experimental flow of gesture recognition

2.3 手势定义

本文设计的是一款体感俄罗斯方块游戏，根据该游戏的基本原理[14]，需要对下落的模型进行右移，左移以及旋转三种控制操作，本文采用手掌右翻，左翻以及上抬三种手势动作与这三种操作对应，图5(a)中为手势的初始状态； (b)为右翻手势； (c)为左翻手势； (d)为上抬手势. 每次游戏控制都是从手势初始状态开始，完成控制操作后返回手势初始状态.

3 实验验证

本文对操作者在坐姿和站姿两种情况下的手腕部右翻、 左翻、 上翻三种动作进行识别，实验中，实验人员对三种动态手势各做 100次，观察阈值判别法与改进KNN算法的识别成功率.

3.1 阈值判别法

阈值判别法作为一种简单直观的判别方法，常被用于传感器信号识别中. 在本文的手势识别中，以手腕右翻为例，实验者做出100次右翻动作以确定阈值，X轴信号如图6 所示，采集到右翻手势的三轴信号初始值、 峰峰值均值及阈值如表1 所示.

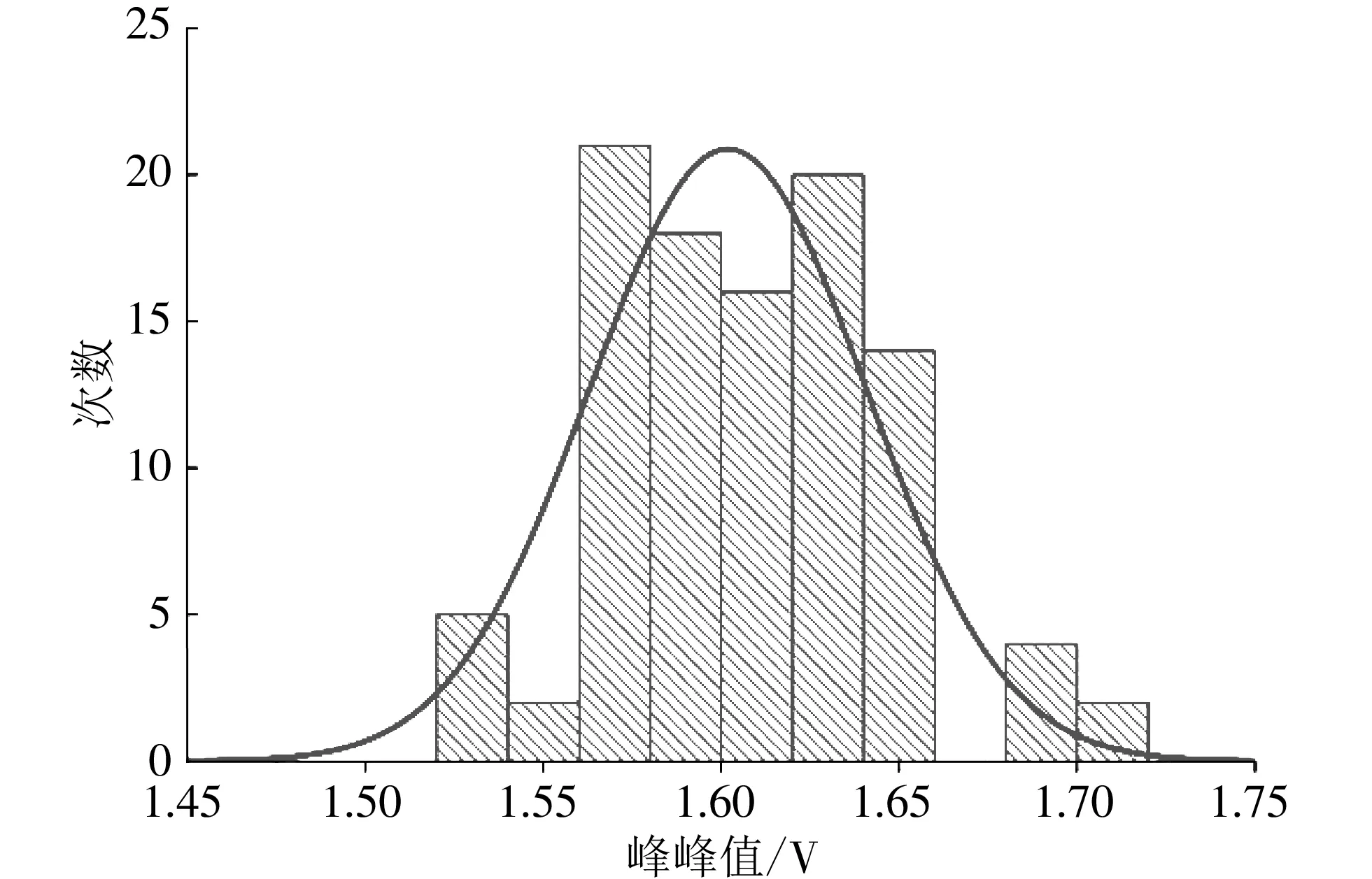
图6 峰峰值的分布Fig.6 Distribution of peak-to-peak values

表1 右翻动态手势参数

经过计算，右翻动作X轴信号峰峰值均值为

EXi=μ=1.601.

(13)

方差为

DXi=σ2=0.039.

(14)

根据本文选取阈值的方法，右翻手势X轴的峰峰值满足中心极限定理

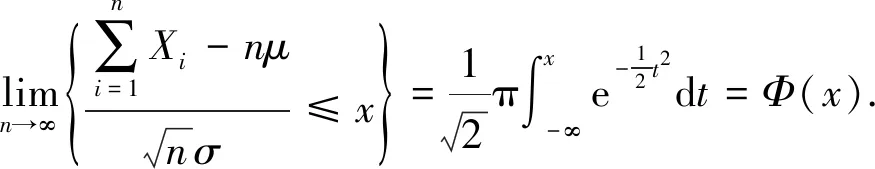
(15)

右翻手势X轴的阈值为

Fi=μ-1.96σ=1.526(V).

(16)

3.2 改进KNN算法

根据改进KNN算法的特征量提取方法，实验开始前，令实验者多次做出三种手势动作，将三种手势信号进行特征量提取并对符号序列编码记录，结果如表2 所示.

表2 训练组手势编码

3.3 实验结果及分析

实验中，实验者将传感器穿戴好后随机做出三个手势动作各50次，记录两种算法的识别成功率.

本文采用识别成功率M衡量手势识别结果的准确率.

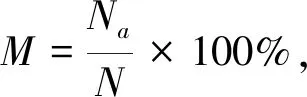
(17)

式中：Na为手势识别正确结果的个数；N为手势动作的总次数.

两种识别方法的识别结果如表3 所示.

表3 改进KNN算法识别成功率对比

由识别结果可以看出，改进KNN算法在手势识别成功率上有一定的提升，约为10%. 阈值判别法在前30次的动态手势识别率较高，在后70次的动态手势识别中识别成功率明显下降，主要原因是在实验过程中，人手的疲劳导致做出的动态手势动作不标准，并且在动作过程中细微的动作也会对阈值判别法的识别造成干扰. 相比阈值判别法，改进KNN算法在动态手势识别当中不易受操作者自身的影响，并且能保证较高的识别成功率.

将改进KNN算法与传统KNN算法相比较，100次随机手势的识别成功率如表4 所示.

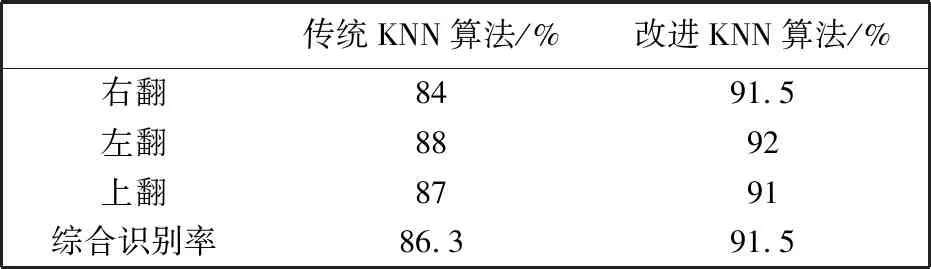
表4 传统KNN算法与改进KNN算法识别结果对比

与传统KNN算法相比，改进KNN算法的识别成功率提升在5%左右，主要原因在于传统KNN算法的训练组数据量过于庞大，而且K值的选取会影响传统KNN算法的识别结果. 而本文的改进KNN算法，不但训练样本较少而且选取K=1即可保证识别率.

4 结 论

本文利用传统KNN算法易实现且无需估计参数的特点，提出了一种优化KNN手势识别算法，实现了对三种手势动作的识别，实验结果证明，在LabVIEW平台搭建的ADXL335体感游戏中，相比阈值判别法，改进KNN算法可以有效提高手势识别成功率. 考虑到动态手势种类众多，未来的研究中将会在保证识别率的情况下进行更多动态手势的识别.