板式电涡流阻尼器的阻尼特性分析
2020-04-29高跃飞
刘 洋,高跃飞,王 登
(中北大学 机电工程学院,山西 太原 030051)
0 引 言
电涡流阻尼器是利用电磁感应原理提供制动力的一种装置,因其在制动过程中器件之间无摩擦,具有噪声小、 可靠性高、 易于控制且维护成本低的优点,在缓冲吸振的工程领域得到了广泛的应用. 1903年,Steckel发明了世界上第一台电磁阻尼器[1]. 自此以后,电磁阻尼器在各个领域都有着广泛的应用. 目前,世界各大知名汽车公司如奔驰、 沃尔沃和依维柯等均将电涡流阻尼器作为辅助装置的标准件应用于多种级别的客车和中、 重型汽车上; 法国的TGV高速动车组和日本的新干线高速列车上均安装了电涡流阻尼器,德国铁路研究中心进行了涡流制动装置的试验并成功将其应用于ICE高速列车上[2]; 作为美国国防部高级研究计划局无人战斗飞行器项目的一部分,美国波音公司和霍尼韦尔公司为X-45A研制了一套电作动刹车系统,另外在民用方面波音公司也为其新一代客机B787提供了电刹车系统[3].
常见的电涡流阻尼器多为圆柱形或筒型结构,近年来板式电涡流阻尼器逐渐成为研究热点. 陈政清等[4-5]提出了板式调谐质量阻尼器,已被上海材料所用于制造世界上最大板式调谐质量阻尼器,安装于上海中心大厦. 汪志昊等[6-7]从构件安装位置、 磁场吸引力对振动频率的影响及磁路优化等方面对摆式电涡流TMD进行优化设计与试验研究. 目前,板式电涡流阻尼器主要应用于高耸塔或超高层建筑等大型结构的抑振领域[7],装置质量高、 体积大. 对于汽车、 火炮等中小型装置而言,板式电涡流阻尼器的研究应用较少,为了扩展板式电涡流阻尼器的应用领域,更有效地提升电涡流阻尼器系统的工作性能,需其进行更深入的研究.
对于常规结构的阻尼器而言,由于其形状规整,较容易根据力学模型推导出阻尼力的计算模型; 但是对于复杂场景下的阻尼器模型,往往很难分析求解出阻尼力,这就需要充分了解电涡流阻尼器的阻尼特性,进而对电涡流阻尼器的应用提供理论指导[8-10]. 本文通过理论推导及Maxwell仿真分析对板式电涡流阻尼器的阻尼特性进行研究,分析了各设计参数对电涡流阻尼力大小的影响,对该类型阻尼器的工程应用具有一定的参考价值.
1 板式电涡流阻尼器结构原理
板式电涡流阻尼器结构简单,可同时实现两个自由度的阻尼力. 图1 为文献[11]提出的电涡流阻尼器,该装置将永磁体与导体板设计成多阵列结构,结构紧凑,制动力大. 阻尼器工作时,永磁体阵列固定,铜导体阵列随运动体在磁体阵列中前后或纵向运动,导体与永磁体发生相对运动,切割磁力线产生涡流阻尼力.
导体板在工作时可以看作由多个不同尺寸的矩形线圈嵌套而成,当导体板与永磁体发生相对运动时,只有在磁场区域内的矩形线圈才会发生磁通量的变化,进而产生感应电流. 将上述装置结构简化为单阵列结构进行阻尼系数分析,只要保证导体处于永磁体磁场区域内即可有感应电流产生. 如图2 所示,磁化电流并非均布于导体中,越靠近导体表面,电流分布越密集. 这是因为导体中心处受到的外界磁力线产生的自感电动势大于导体表面处的自感电动势,自感电动势抵抗住电流的流动,进而产生了集肤效应. 因此,阻尼器气隙中任一点磁感应强度大小均取决于磁体表面环形电流的强弱.

图1 多阵列板式电涡流阻尼器Fig.1 Multi-array plate eddy current damper

图2 导体的集肤效应Fig.2 Skin effect of conductor
2 板式电涡流阻尼器阻尼系数理论模型
图3 是永磁体磁场,根据安培分子环流假说[12],取永磁体上厚度为dz0的电流环A′B′C′D′A′进行理论分析,设该电流环的电流强度为I,永磁体外一点P(x,y,z)处产生的磁感应强度为dB,其表达式为

(1)
式中: dBx、 dBy和dBz是电流环A′B′C′D′A′在P点处磁感应强度的三个轴向分量. 而dB是由A′B′、B′C′、C′D′和D′A′综合作用叠加而成的.
为探究矩形永磁体磁阻尼系数的影响因素,需推导出永磁体的三维磁场解析式模型,以便后续有限元仿真计算分析.
为了简化计算过程,下面只取A′B′段进行计算,其余段均可参考A′B′段的计算过程.
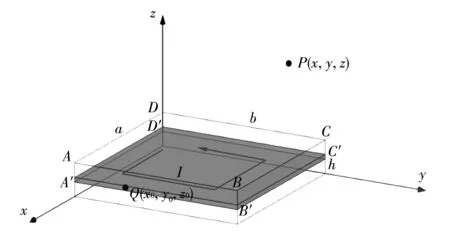
图3 矩形永磁体磁场分析原理图Fig.3 Schematic diagram of magnetic field analysis of rectangular permanent magnet
根据Biot-Savart定律,P点处的磁感应强度为
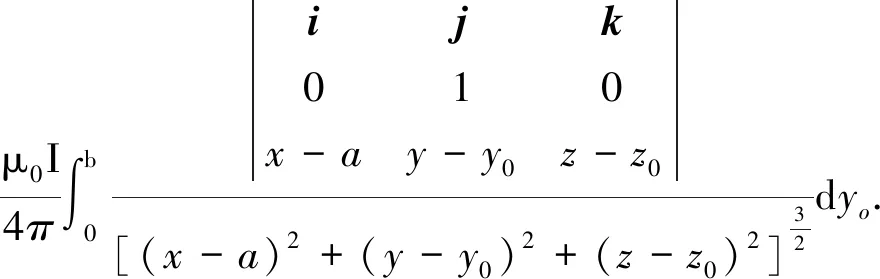
(2)
由此可求得三个坐标轴分量为

(3)
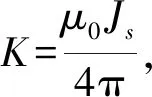
dBx=dBx1+dBx2+dBx3+dBx4=
(4)
dBy=dBy1+dBy2+dBy3+dBy4=
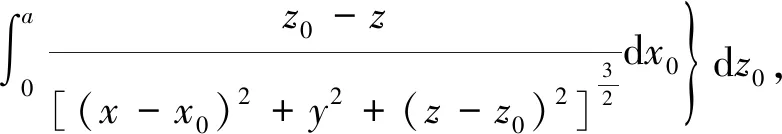
(5)
dBz=dBz1+dBz2+dBz3+dBz4=
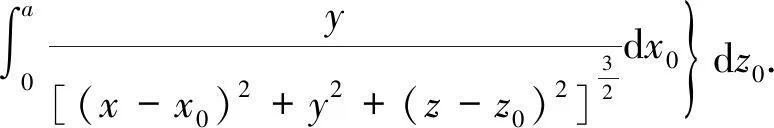
(6)
综上,对Z轴方向求积分即可以推出永磁体ABCD在P点处的磁场强度

(7)
式中: 中间函数Γ和Φ表达式为
Γ(δ1,δ2,δ3)=

(8)
Φ(φ1,φ2,φ3)=

(9)
由法拉第电磁感应定律可知,电磁感应电动势为
E=Blvsinθ,
(10)
式中:l为导体长度;v为导体板切割磁感线的运动速度;θ为导体运动方向和磁力线方向间的夹角.
根据安培定律可知,感应涡流阻尼力为
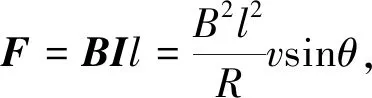
(11)

(12)
式中:ρ为导体电阻率;S为横截面积. 由式(11)可推算出阻尼系数的影响参数
ζ=ζ(a,b,h,l,R,θ,r).
(13)
3 有限元仿真分析
运用Maxwell电磁场仿真软件对上述单阵列结构进行分析,采用静磁场分析模块建立三维电磁场有限元模型(模型参数见表1),将模型中对涡流阻尼力影响因数小的部分视为空气处理. 永磁体采用钕铁硼永磁体,牌号为N35; 导体材料选用铝.

表1 有限元模型参数
图4 是不同气隙高度下电涡流阻尼器阻尼系数的变化特性曲线. 由图可知,磁阻尼系数随气隙高度的增加而减小. 当气隙高度低于2 mm时,随着气隙高度的增加,磁阻尼系数骤降; 当气隙高度大于10 mm后,磁阻尼系数低于10 Ns/m. 由此说明,为获得较大的阻尼系数,需尽量减小气隙高度,但考虑到实际加工工艺精度,一般气隙高度选择1~2 mm即可获得较好的阻尼器性能.

图4 不同气隙高度下的磁阻尼系数Fig.4 Magnetic damping coefficients at different air gap heights
不同磁体厚度下电涡流阻尼器阻尼系数如图5 所示. 当磁体厚度较低时,阻尼系数随着磁体厚度的增加而增加,当磁体厚度超过18 mm后,增加磁体厚度对提升气隙磁阻尼大小影响较小. 磁体厚度从18 mm增加到20 mm,阻尼系数增加了0.6%.
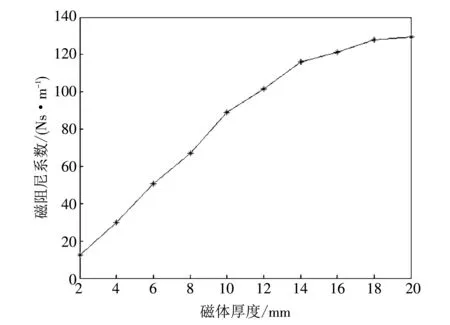
图5 不同磁体厚度下的磁阻尼系数Fig.5 Magnetic damping coefficients at different magnet thicknesses
导体板厚度与阻尼系数之间的关系如图6 所示,当h′<8 mm时,阻尼系数随着导体板厚度的增加而增加; 当h′>8 mm时,阻尼系数受导体板厚度影响较小. 这是因为电涡流的趋肤效应一方面增大了导体板的电阻,另一方面由于电涡流集中于导体表面,因此所受的洛伦兹力减小,阻尼系数相应变小.

图6 不同导体厚度下的磁阻尼系数Fig.6 Magnetic damping coefficients at different conductor thicknesses
图7 给出了永磁体间距p与阻尼系数的关系. 由图可知,当p<4.8 mm时,阻尼系数随永磁体间距p的增大而增大; 当p>4.8 mm时,阻尼系数随永磁体间距p的增大而减小; 当p=4.8 mm 时,阻尼系数取最大值.
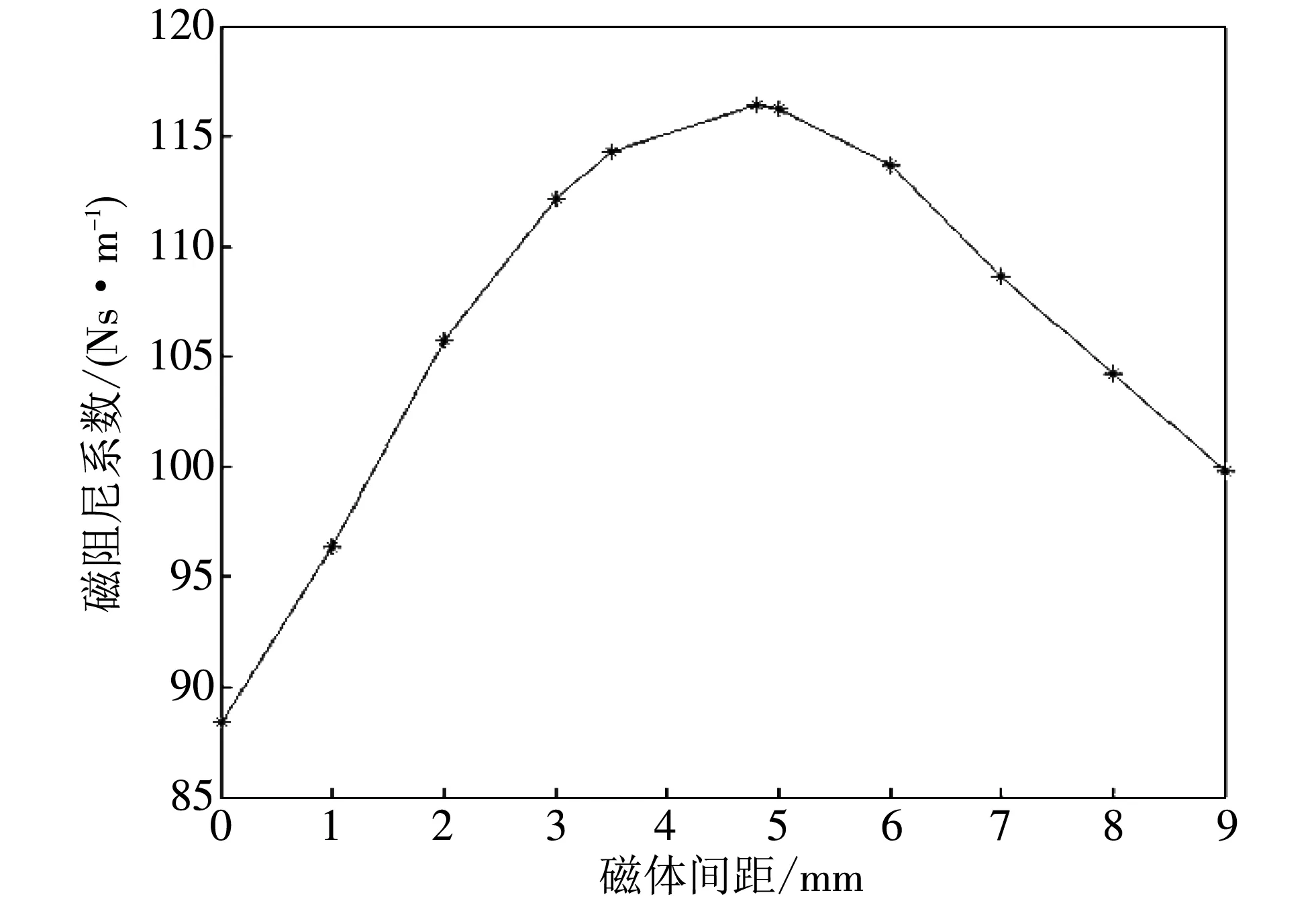
图7 不同永磁体间距下的阻尼系数Fig.7 Damping coefficients at different permanent magnet spacing
4 结 论
基于Biot-Savart定律,推导了板式永磁体周围空间内任意点处的磁感应强度表达式,建立了不同结构参数对阻尼系数影响的理论模型,通过电磁场有限元分析法进一步研究了部分参数对电涡流阻尼器阻尼性能的影响规律. 主要结论如下:
1) 板式电涡流阻尼器结构简单紧凑,制动力大,阻尼比易调节且能实现双自由度阻尼控制.
2) 在一定范围内,增加磁体及导体厚度、 永磁体间距可以显著提高电涡流阻尼器的阻尼系数,提高结构性能.
3) 在考虑零件加工及装配成本等实际问题时,尽可能降低气隙高度可以有效增强气隙磁感应强度,有利于提升电涡流阻尼器的阻尼特性.
4) 板式电涡流阻尼器输出稳定,避免了传统阻尼器复杂的控制系统和结构设计,有利于系统的轻量化和机动性能的提升.
