基于改进遗传算法的有限推力远程导引变轨策略

刘俊尧，贾建芳，李文强，宋锦武

(1. 中北大学 电气与控制工程学院，山西 太原 030051； 2. 中北大学 信息与通信工程学院，山西 太原 030051；3. 广州广电计量检测股份有限公司，广东 广州 510656)

0 引 言

航天器轨道转移优化技术是空间技术的重要组成部分. 目前对于轨道转移优化的研究大多基于脉冲变轨[1]. 在真实工作状态下进行轨道转移时，由于发动机推力制约，脉冲式变轨并不符合轨道转移的实际情况[2]，特别是发动机推力较小的航天器在远距离轨道转移时，所需时间较长，存在很长的推力弧段，此时脉冲式变轨假设不再成立[3]. 与脉冲式轨道转移技术相比，基于有限推力的轨道转移技术能够真实反映航天器的工作状态，在提高研究结果真实性、 精确性方面有很大的优越性.

基于有限推力的航天器轨道转移优化问题的本质是泛函空间最优控制问题[4]，根据优化过程中对动力学模型有限维近似处理方式不同，大致分为间接法、 直接法和混合法三种. 间接法[5-7]的本质是以极小值原理以及非线性规划作为理论基础，通过相应的边界条件将轨道转移优化问题转化为两点边值求解问题，虽能得到很光滑的解, 但由于对初始猜测异常要求很高，求解时困难较大； 直接法[8-10]的一般思路是对待优化轨道进行离散处理，利用优化算法在每一个轨道段内求解若干个待优化参数，转化后待优化参数较多，需要在很大范围内进行参数搜索，计算性能随着节点数增加会有较大程度下降，算法鲁棒性较差； 混合法[11-13]研究以优化算法的实现为主要方向，对问题本身具有很大依赖性，求解时需要针对具体问题对算法做大量修改.

智能优化算法[14-17]是一种启发式优化算法，一般是针对具体问题设计相关的算法，智能优化算法技术性、 应用性强，计算速度快且理论要求不高，得到国内外学者广泛关注并且发展迅速.

针对有限推力下远程导引变轨问题，本文采用改进遗传算法求解远程轨道能量最优的多脉冲变轨策略，将求解得到的多脉冲变轨策略在变轨点转换为推力弧段上的有限推力，通过发动机推力计算出航天器加速度，对加速度进行积分求得航天器瞬时速度增量，将速度增量不断累加完成变轨，实现有限推力下远程导引变轨，并对有限推力下远程导引变轨策略速度增量方向进行修正，修正后变轨策略精度有较大程度提高，与目标轨道位置误差大幅减小，能够反映航天器在真实工作状态下的轨道转移情况.

1 远程导引变轨原理

1.1 特殊点变轨

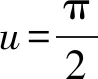
根据特殊点变轨特点，变轨方案如图1 所示.

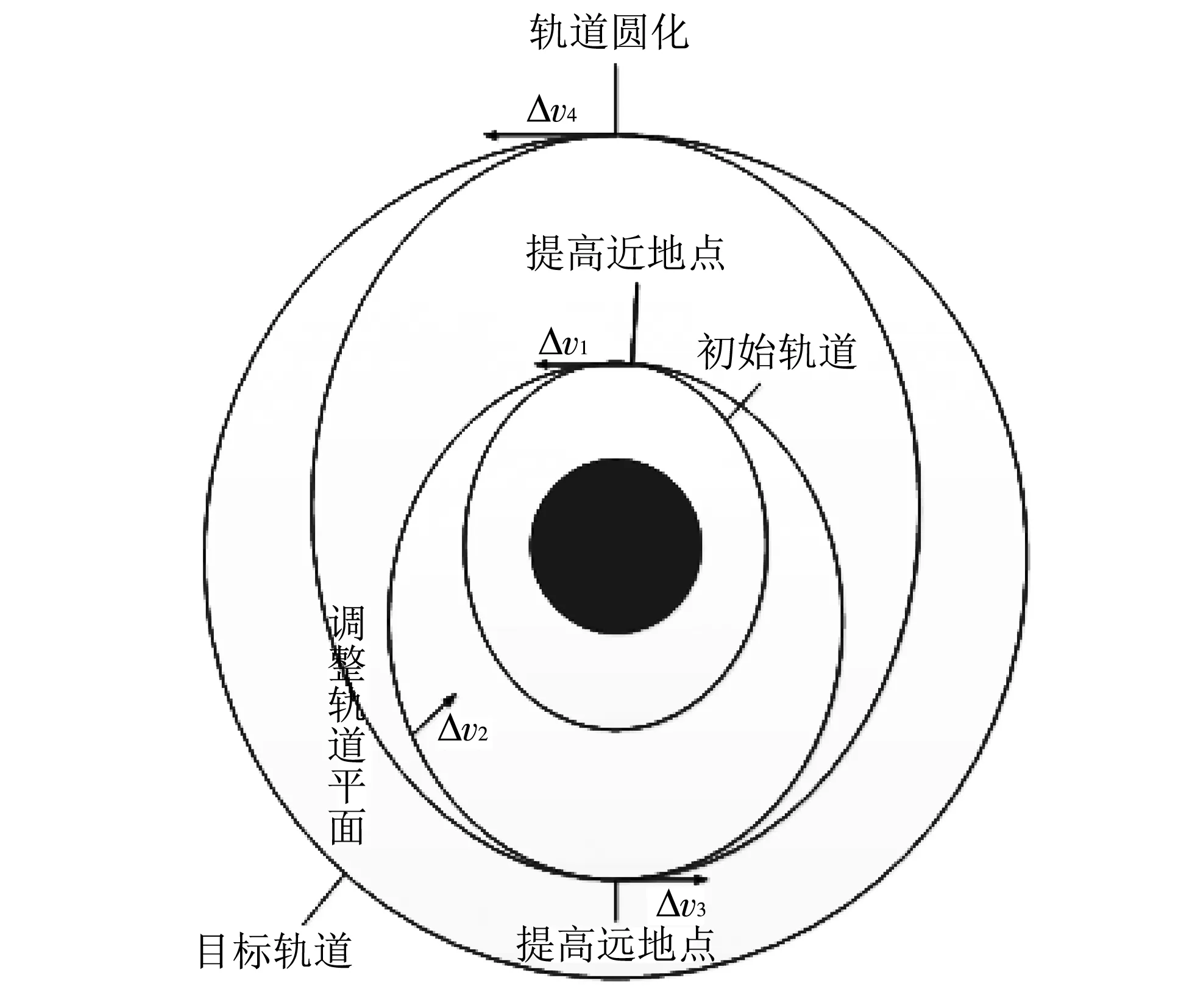
图1 特殊点变轨方法Fig.1 Special point change method

特殊点变轨大致分为四步：

1) 调整近地点高度： 初始轨道远地点处施加迹向脉冲量Δv1；

2) 调整轨道倾角： 纬度幅角为0或π处施加法向脉冲量Δv2，将异面轨道调整为共面轨道；

3) 调整远地点高度： 转移轨道近地点处施加迹向脉冲量Δv3；

4) 调整轨道偏心率： 在目标轨道远地点处施加迹向脉冲量Δv4，实现椭圆轨道向圆轨道转换.

1.2 脉冲量计算

二体条件下，基于轨道动力学方程，根据变轨前的轨道参数和变轨后轨道参数，可以求得每次变轨所需要脉冲量，每次施加脉冲量计算如下：

第1次变轨

(1)

第2次变轨

(2)

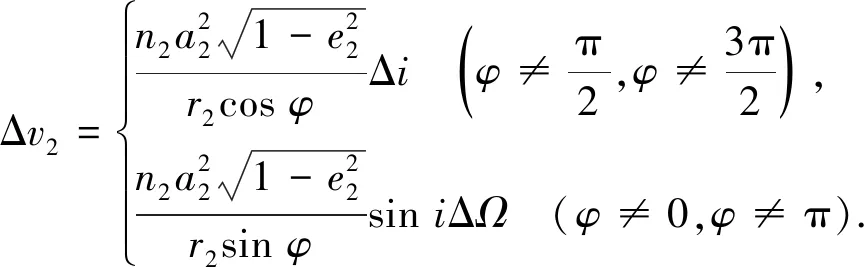
(3)

第3次变轨

(4)

第4次变轨

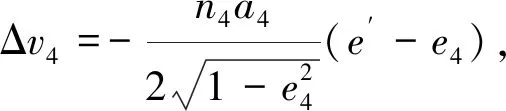
(5)

式中：n表示轨道角速度；e表示轨道偏心率；hp表示近地点高度；ha表示远地点高度； Δi表示轨道倾角修正量； ΔΩ表示升交点赤经修正量；r表示航天器地心距；a表示轨道半长轴.

1.3 脉冲量转换为有限推力方法

根据初始轨道参数和目标轨道参数求解得到脉冲量，将脉冲量根据航天器发动机推力、 比冲在发动机工作时间段内转换为有限推力，将长时间变轨过程转换为短时间内的连续变轨，转换方法如图2 所示.

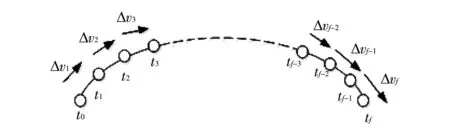
图2 脉冲量向有限推力转换Fig.2 Pulse thrust to finite thrust conversion

图2 中，ti表示连续变轨过程中的时间节点，Δvi表示速度增量.

在轨道转换过程中，需要确定发动机开始工作时间、 终止工作时间以及发动机产生的加速度.

发动机工作时间为

(6)

式中：tb为发动机开始工作时刻；tf为发动机工作终止时刻；M为发动机消耗燃料的质量；F为发动机提供的推力. 发动机燃料消耗量M由航天器质量、 发动机比冲以及速度增量决定，计算公式为

(7)

式中：m为航天器质量； Δv为速度增量；isp为发动机比冲.

1.4 有限推力转换修正

在脉冲变轨向有限推力变轨转换过程中，在轨道转移弧段对发动机推力产生的航天器加速度进行积分，求得节点处的速度增量. 在qsw本地轨道坐标系中，X′轴是从地球中心指向卫星的单位矢量；Z′轴是垂直卫星轨道平面且方向向上的单位矢量；Y′轴是由(x,y,z)形成规则确定的单位矢量，如图3 所示.

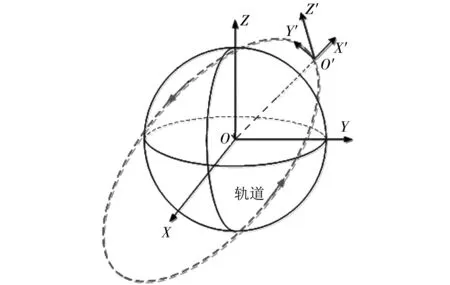
图3 本地轨道坐标系Fig.3 Local orbital coordinate system

图3 中，O-XYZ是ECI坐标系，O′-X′Y′Z′是qsw本地轨道坐标系. 在qsw本地轨道坐标系中，轨道为圆轨时，Y′轴方向为轨道切线方向，与航天器速度方向一致； 轨道为近圆轨道时，Y′轴方向与椭圆轨道切线方向存在少量偏差，与航天器速度方向基本保持一致.

在脉冲变轨向有限推力变轨转换过程中，将qsw本地轨道坐标系Y′轴方向近似为速度增量方向，通过确定节点处航天器速度矢量，计算速度增量方向.

2 遗传算法

遗传算法是一种高效、 并行的全局搜索方法. 它的求解过程是基于概率搜索技术，以目标函数值作为搜索目标，同时在多个搜索点对目标进行搜索. 标准遗传算法全局最优搜索能力强，但是在实践应用中，也存在局部搜索能力差的问题，无法保证算法完全收敛. 针对标准遗传算法存在的问题，对遗传算法的选择和交叉操作进行改进，在对群体根据适应度值高低进行排序的基础上，用个体最优与其他偶数位的所有个体进行交叉，每次交叉产生两个新的个体，在交叉过后，对新产生的群体进行多点变异产生子群体，再计算其适应度值，然后与父群体合并，并且根据适应度值进行排序，取前NP个个体为新群体，进行下一次遗传操作. 改进遗传算法运算流程如图4 所示.

二体条件下，式(1)中的n1、e1、hp由初始轨道根数确定； 式(3)中的n3、e3由初始轨道根数及Δv1确定，h′a为目标轨道远地点高度，ha为初始轨道远地点高度； 式(5)中的n4、a4、e4由目标轨道根数确定. 选取第1次变轨时转移轨道近地点高度h′p为唯一优化变量，参数设置如下： 基因数目D=1； 染色体数目NP=100； 最大遗传代数G=1 000； 交叉概率Pc=0.8； 变异概率Pm=0.1. 构建目标函数

fmin=Δv=∑(|Δv1|+|Δv2|+|Δv3|).

(8)

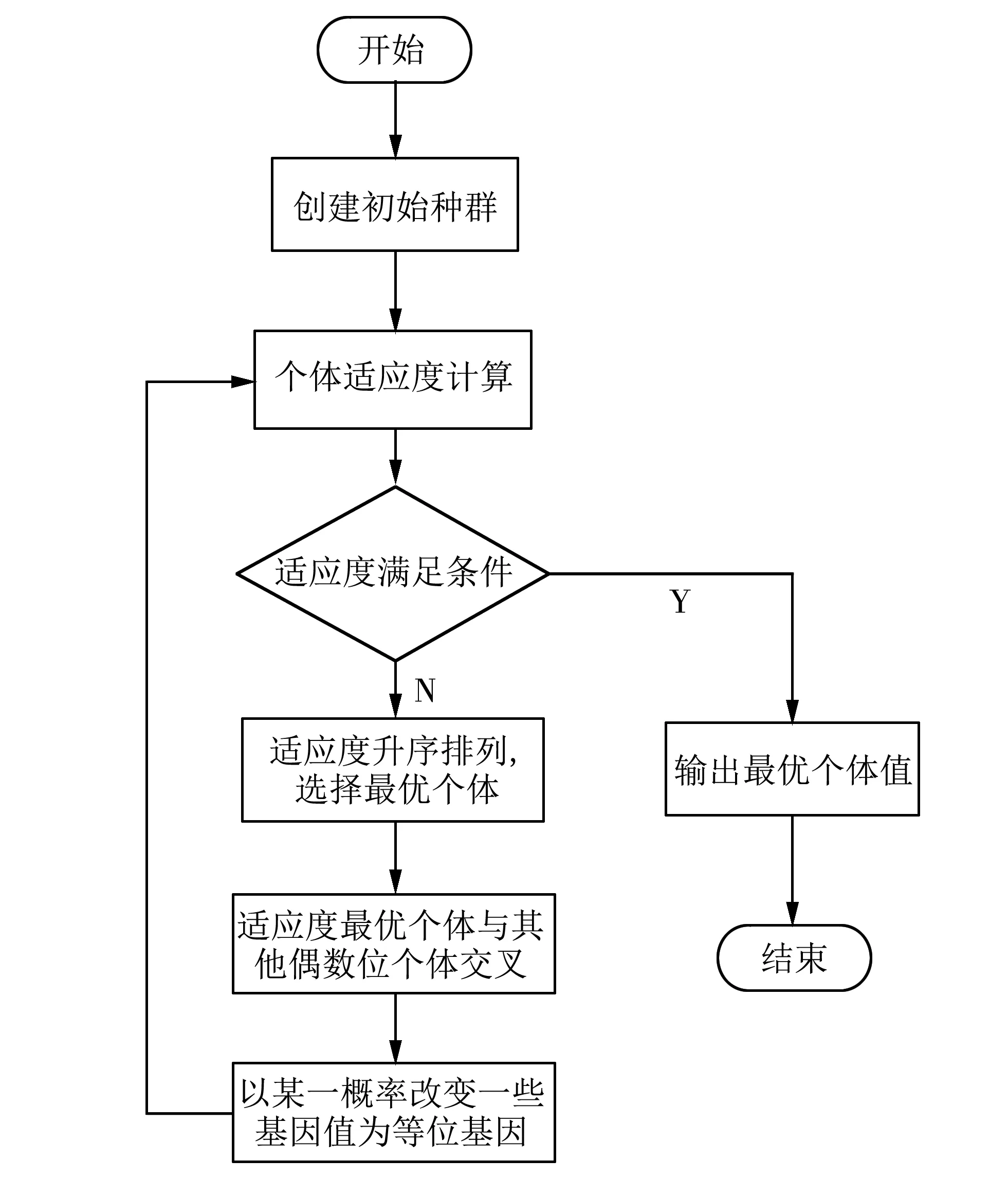
图4 改进遗传算法流程图Fig.4 Improved genetic algorithm flow chart

改进遗传算法求解h′p最优解时，先计算Δv1、 Δv2、 Δv3的适应度并按升序排列，选择适应度最高的Δv1、 Δv2、 Δv3染色体个体与其他偶数位的所有染色体个体进行交叉并进行多点变异产生子代染色体Δv′1、 Δv′2、 Δv′3，计算子代染色体适应度并按升序排列，将Δv′1、 Δv′2、 Δv′3染色体与Δv1、 Δv2、 Δv3染色体合并，计算合并后的适应度并按升序排列，选取前NP个适应度最高值作为此代最优个体.

3 仿真算例与分析

3.1 轨道根数设置

初始轨道根数和目标轨道根数设置如表1. 表1 中，a表示轨道半长轴；e表示偏心率；i表示轨道倾角；Ω表示升交点赤经；ω表示近地点幅角；anv表示真近点角.

由于初始轨道与目标轨道共面，无需改变轨道倾角，仅需要施加3次脉冲量，实现远程导引变轨.

表1 轨道根数参数

3.2 仿真结果与分析

以第一次变轨时转移轨道近地点高度h′p为优化变量，采用改进遗传算法求解总速度增量的最小值. 结果显示，当h′p为6 982.039 km时，总速度增量最小值为66.699 m/s，其中第1次变轨的速度增量Δv1为28.855 m/s，第2次变轨的速度增量Δv2为33.122 m/s，第3次变轨的速度增量Δv3为 4.722 m/s，航天器远程导引变轨序列如表2 所示.

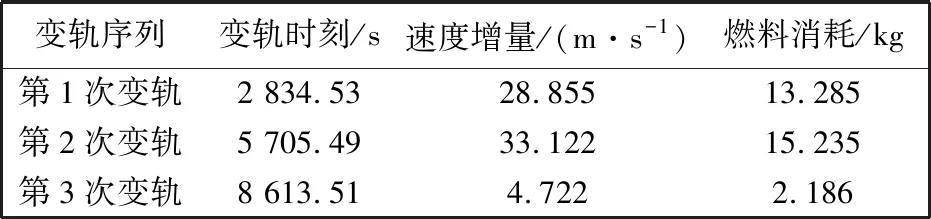
表2 脉冲变轨方案

将初始得到的脉冲变轨方案在变轨点处转换为推力弧段上的有限推力，设置航天器初始质量为1 000 kg，发动机比冲为220 s，分别施加50 N, 100 N, 200 N的推力，转换结果如表3 所示.

表3 50 N推力下变轨方案

表4 100 N推力下变轨方案

由表3～表5 可知，有限推力变轨方案消耗的燃料会多于脉冲变轨方案； 推力越小，轨道上推力弧段越长，变轨结果误差越大. 由表5可知，推力为200 N时，航天器在经过3次变轨后，轨道半长轴为6 998.295 km，与目标轨道半长轴误差为1.715 km，相对位置误差为3.89 km. 转换后的连续推力变轨方案速度不断迭加，在不同节点处不断变化，但速度增量方向一直保持脉冲变轨处方向不变，对转换结果造成较大影响，并且变轨持续时间，误差越大. 对200 N推力下变轨方案进行修正，结果如表6 所示.

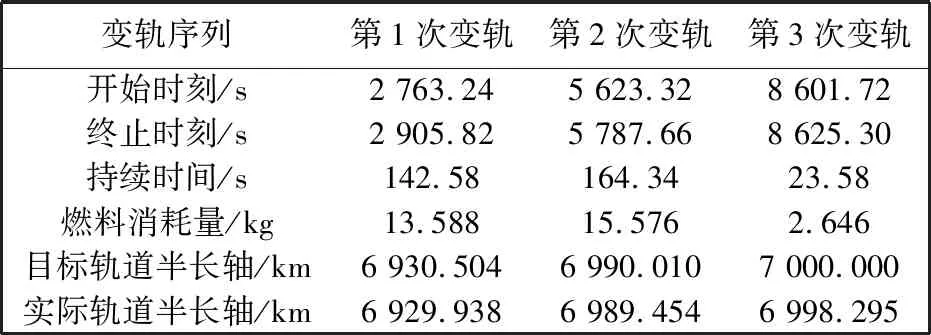
表5 200 N推力下变轨方案

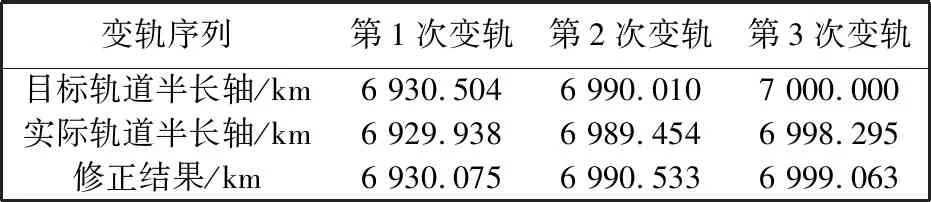
表6 有限推力变轨方案修正结果

由表6 可知，有限推力变轨转换修正方案精度更高，与目标轨道半长轴误差为0.957 km，相对位值误差为1.33 km. 经过3次变轨，轨道根数与目标轨道根数对比如表7 所示.

表7 轨道根数对比

表7 中，真近点角差异是由于推力弧段的存在，导致变轨结束时刻有差异. 由表7 可知，脉冲变轨方案转换为有限推力方案，仅有轨道半长轴、 偏心率、 真近点角存在少量差异，轨道倾角、 升交点赤经、 近地点幅角保持一致； 有限推力修正方案精度更高，可以反映航天器在真实飞行环境中的变轨情况. 航天器有限推力方案变轨仿真结果如图5 所示.

由图5 可知，变轨后轨道高度提升，轨道仍为圆轨； 由图6 可知，航天器轨道半长轴在机动时间段内不断增大，非机动时间段内基本保持不变，经过3次变轨，轨道半长轴与目标轨道半长轴高度一致.

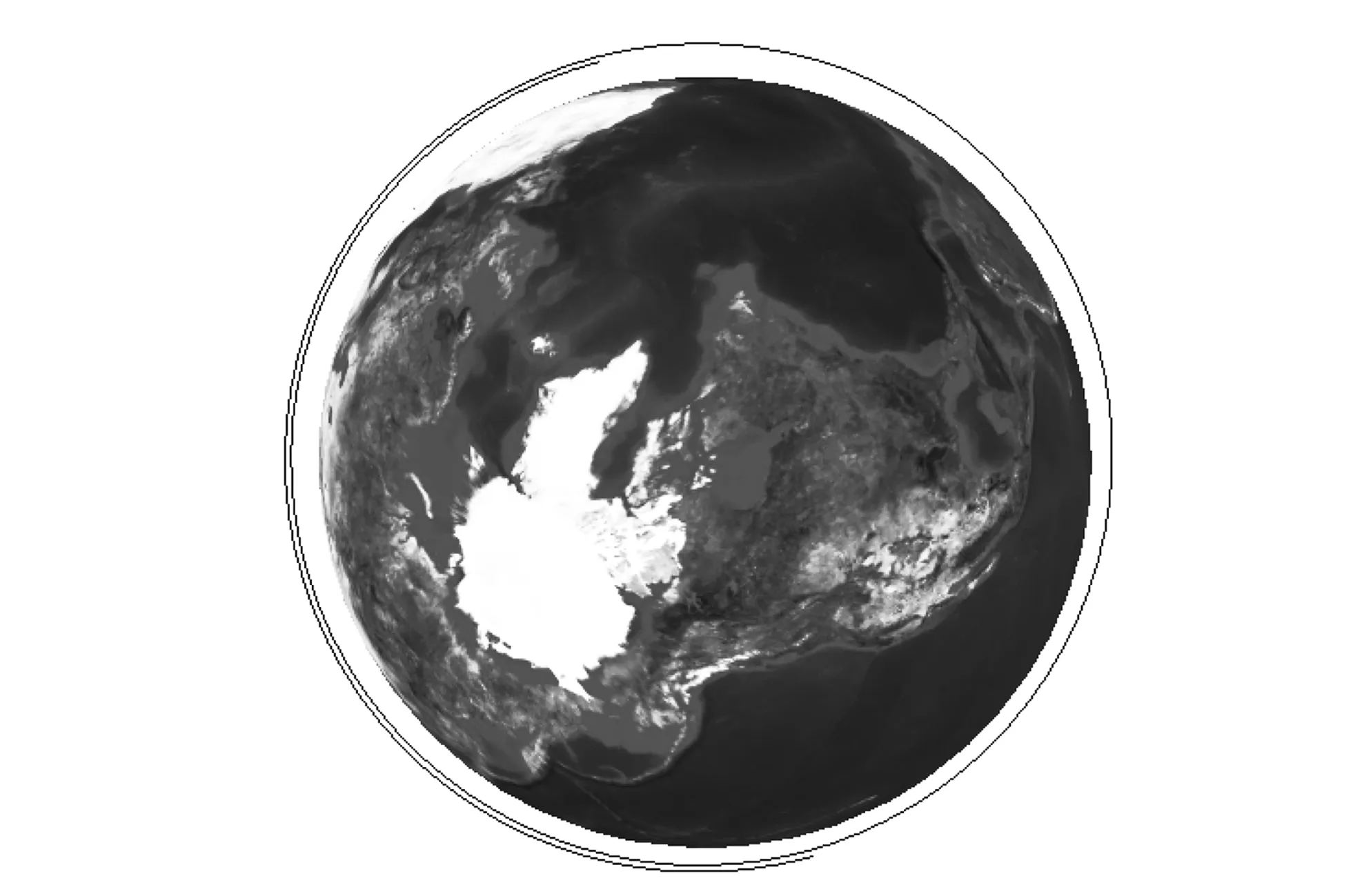
图5 有限推力方案3D仿真图Fig.5 Finite thrust scheme 3D simulation diagram

与脉冲变轨相比，有限推力变轨所需燃料更多，是由于有限推力变轨弧段存在引力损失； 不进行推力方向修正的变轨方案的误差要高于进行推力方向修正的变轨方案，是因为通过修正推力方向可找到时间节点处推力的方位角和俯仰角.

4 结 论

本文对有限推力下远程导引变轨进行了研究. 通过改进遗传算法的选择和交叉操作，求解得到燃料最优的多脉冲变轨方案，在脉冲点处将脉冲量转换为推力弧段上的有限推力，实现多脉冲机动远程导引变轨向有限推力下远程导引变轨的转换，并对有限推力变轨方案速度增量方向进行修正，修正结果精度有较大程度提高，证明方法确实有效. 基于有限推力的远程导引变轨方案可以反映航天器在真实工作状态下环境中变轨的过程，并取得较高的精度.