公共卫生教育的双斑块SIR传染病模型的敏感性分析
2020-04-29李桂花
郭 刚,李桂花
(中北大学 理学院, 山西 太原 030051)
0 引 言
近年来,随着人类社会发展对生态环境的影响,导致突发传染病(如SARS)与一些死灰复燃的传染病(比如疟疾)频频出现,这些传染病都给人们带来了巨大的损失[1-5]. 而往往传染病的爆发都会引起人们的恐慌,这很不利于疾病的控制及社会的稳定,故增加人们对疾病的了解将变得尤为重要. 另外,随着社会经济的发展,人们之间的交往越来越频繁,这就更加速了疾病的传播. 这就表明了公众卫生教育及斑块迁移对疾病传播影响研究的重要性. 公共卫生教育包括大众教育和人际传播[2],大众教育指人们通过网络、 电视等媒体获得疾病信息. 人际传播指人和人之间通过交流获得疾病信息.
建立动力学模型分析疾病传播机理是一种常用的办法,本文将考虑公共卫生教育和斑块迁移对传染病动力学模型的影响. 研究公共卫生教育及斑块迁移对传染病影响的文献有很多[2-7],其中,一部分通过不同的非线性发生率函数(如μe-mI)来刻画公共卫生教育的影响[4-5],另一部分则将易感人群分为有疾病意识和无疾病意识两类人群[2-3,6]. 当个体拥有疾病防护意识则会降低其被传染概率. 将人口分为两个斑块,分别记S11、S12、I1和R1为第一个斑块中有疾病意识易感人群、 无疾病意识易感人群、 感染人群和恢复人群,S21、S22、I2和R2则表示第二个斑块中相应的人群. 记单位时间内,i斑块中新增加的有疾病意识人数为σiSi1Si2,被感染的有疾病意识人数为βi1Si1Ii,被感染的无疾病意识人数为βi2Si2Ii,则模型如下:

(1)
式中:λij表示第i个斑块中j类人群人口的输入;μi和γi分别表示第i个斑块中人口的自然死亡率和恢复率;ηi和σi分别表示第i个斑块中的大众传播力度和人际传播力度;βi1表示i斑块中无疾病意识人群的感染率;βi2表示i斑块中有疾病意识人群的感染率,显然有βi1>βi2;mij表示第i个斑块向第j个斑块的迁移率.
本文首先分析了模型各参数的敏感性,确定疾病传播的敏感参数. 然后分析了各敏感参数对疾病传播的具体影响,确定疾病传播的主要因素.
1 敏感性分析
敏感性分析指通过一系列的测试,使用不同的输入参数来观察预测参数值的变化如何影响系统的动态行为,识别输入参数与预测参数之间的关系[7-8]. 通过敏感性分析可以帮我们确定不同参数对疾病传播和流行的相对重要性. 本节主要分析参数η1,η2,σ1,σ2,m12,m21,β11,β12,β21,β22,γ1,γ2的敏感性,采用LHS/PRCC和灵敏度指标法分别对模型基本再生数和地方病平衡点进行敏感性分析,确定影响疾病传播的重要参数.
1.1 基本再生数的敏感性分析
采用下一代矩阵法求模型的基本再生数[9],基本再生数R0为下一代矩阵的谱半径. 运用文献[9]中的方法,可以得到以下两个矩阵

(2)
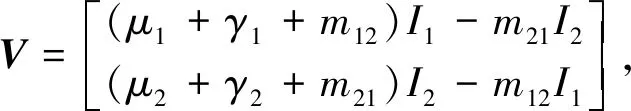
(3)
式中:F表示新的被感染个体出现的速率,V=V--V+,V-表示感染个体离开感染仓室的速率,V+表示非感染个体进入感染仓室的速率. 分别计算F和V在E0处的导数,并记
f=β11S011+β12S012,
(4)
g=β21S021+β22S022,
(5)
m=μ1+γ1+m12,
(6)
n=μ2+γ2+m21,
(7)
D=mn-m12m21,
(8)
得到
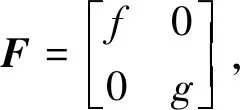
(9)

(10)
则
R0=ρ(FV-1)=
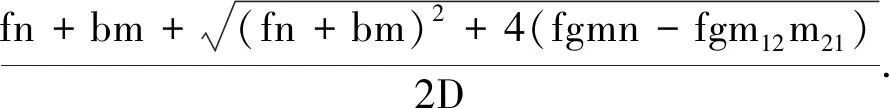
(11)
本节通过LHS/PRCC法对模型基本再生数进行敏感性分析. LHS/PRCC法即拉丁超立方抽样/偏秩相关系数法,是一种全局性的参数敏感性分析方法,可以快速有效识别模型中非线性和单调的敏感参数,适用于多个变量之间的相关分析[7]. 偏秩相关系数(PRCC)绝对值越大相关性越强,值为正(负)代表正相关(负相关). 根据表1 参数的取值范围,利用LHS方法随机选取12个参数的1 000个样本,并且每个参数都服从一个正态分布,通过MATLAB数值模拟得出PRCC值.
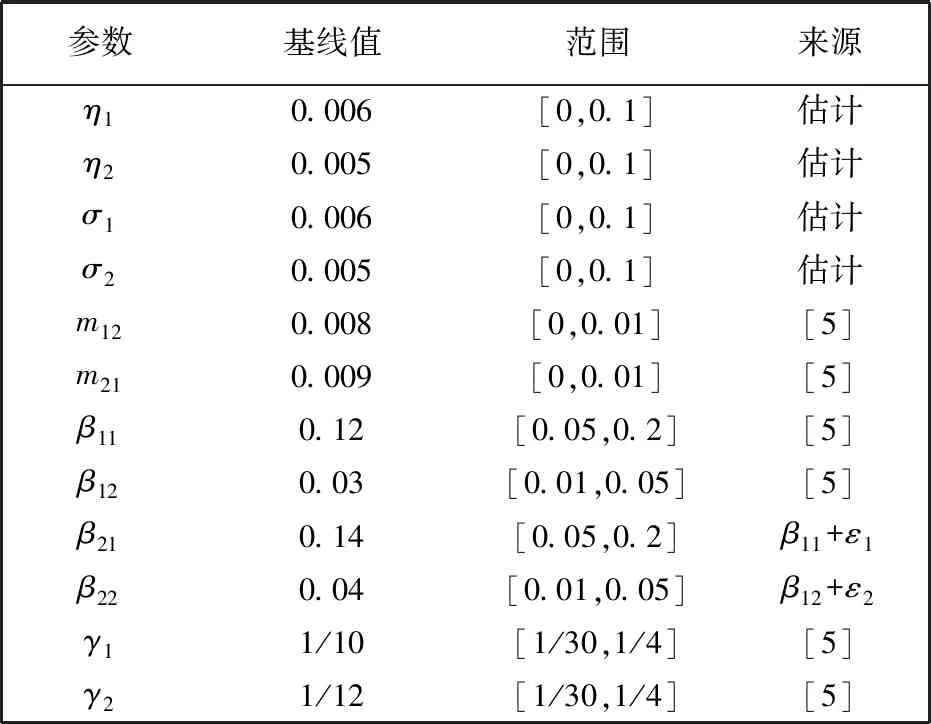
表1 参数取值
如图1 所示,参数η1,η2,σ1,σ2,m21,γ1,γ2与基本再生数负相关,其中γ2相关性最强,其次为γ1,σ2,σ1,η2,η1. 所以,虽然公众卫生教育可以减缓疾病的传播,但相应治疗水平的提高更为重要. 参数m12,β11,β12,β21,β22与基本再生数正相关,其中β22相关性最强,其次为β12,β21,β11,m12.

图1 PRCC值Fig.1 PRCC value
1.2 地方病平衡点的敏感性分析
灵敏度指标是变量相对变化与参数相对变化的比值,通过灵敏度指标的分析,可以测量参数变化时状态变量的相对变化[8]. 灵敏度指标值的绝对值越大参数敏感性越强,值为正(负)代表正相关(负相关). 根据文献[10]中计算灵敏度指标的方法,记变量(S11,S12,I1,R1,S21,S22,I2,R2)为(x1,x2,…,x8); 参数(Λ11,μ1,η1,σ1,β11,m12,m21,Λ12,β12,γ1,Λ21,μ2,η2,σ2,β21,Λ22,β22,γ2)为(y1,y2,…,y18). 则八个平衡方程为
f1(x1,…,x8;y1,…,y18)=y1-y2x1-y3x1-
y4x1x2-y5x1x3-y6x1+y7x5=0,
(12)
f2(x1,…,x8;y1,…,y18)=y8-y2x2+y3x1+
y4x1x2-y9x2x3-y6x2+y7x6=0,
(13)
f3(x1,…,x8;y1,…,y18)=-y2x3-y10x3+
y5x1x3+y9x2x3-y6x3+y7x7=0,
(14)
f4(x1,…,x8;y1,…,y18)=-y2x4+y10x3-
y6x4+y7x8=0,
(15)
f5(x1,…,x8;y1,…,y18)=y11-y12x5-y13x5-
y14x5x6-y15x5x7+y6x1-y7x5=0,
(16)
f6(x1,…,x8;y1,…,y18)=y16-y12x6+y13x5+
y14x5x6-y17x6x7+y6x2-y7x6=0,
(17)
f7(x1,…,x8;y1,…,y18)=-y12x7-y18x7+
y15x5x7+y17x6x7+y6x3-y7x7=0,
(18)
f8(x1,…,x8;y1,…,y18)=-y12x8+y18x7+
y6x4-y7x8=0,
(19)
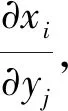
(i=1,…,8;j=1,…,18).
(20)
当l≠j,有
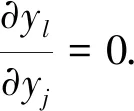
(21)
进而
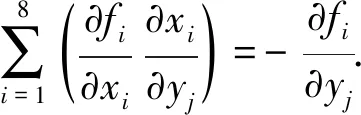
(22)
令
AXj=Yj,
(23)


(i=1,…,8;j=1,…,18).
(24)
根据文献[10]中方法,取表1 中参数基线值,通过MATLAB数值模拟,得出地方病平衡点的灵敏度指标,见表2.
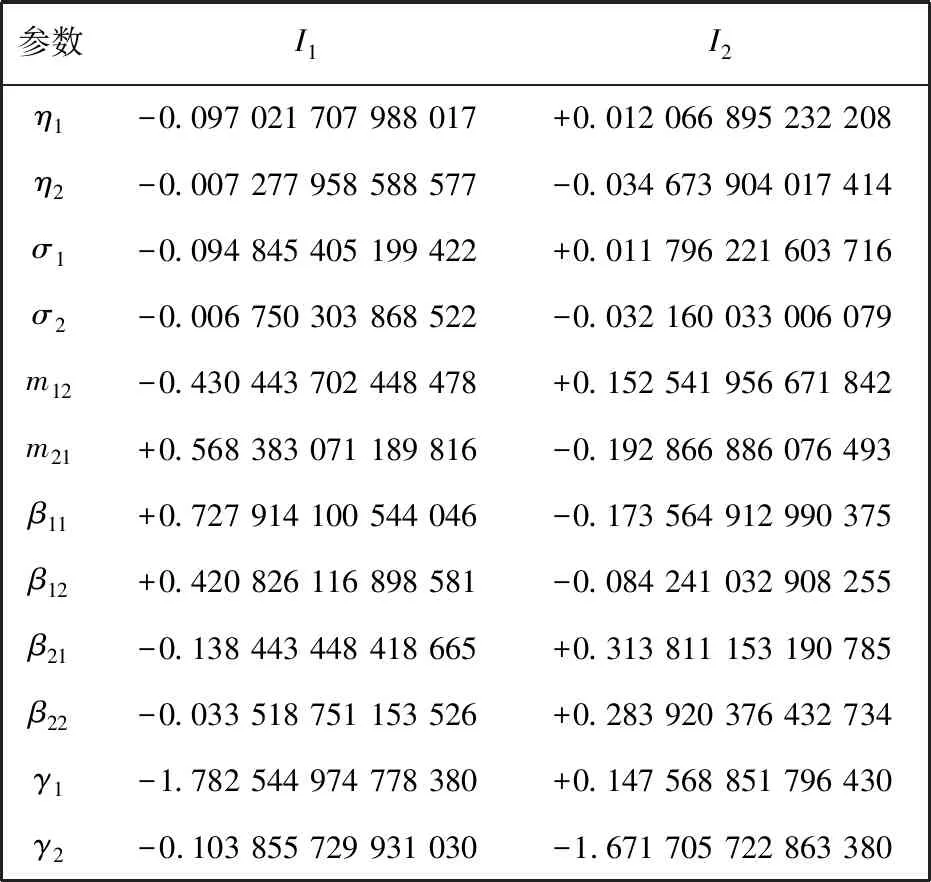
表2 地方病平衡点灵敏度指标
通过表2 可以观察每个参数对各斑块疾病传播的影响. 其中每个斑块中的恢复率与疾病流行程度的负相关性最强,说明治疗水平是控制疾病传播最主要的因素; 无疾病意识人群的感染率与疾病流行程度的正相关性最强,这就要求加强公共卫生教育,促进无疾病意识人群进入有疾病意识人群. 另外,m12与I1呈负相关,与I2呈正相关,m21则相反,说明人口的迁出都有利于本地区疾病传播的控制,但不利于其他斑块疾病传播的控制.
2 疾病的影响因素
影响传染病的传播因素多种多样,公共卫生教育力度、 疾病防护的反应时间、 疾病信息的正确性、 人口流动及医疗水平,都对疾病的传播有很大的影响,本节将通过MATLAB数值模拟来分析这些因素对疾病传播的具体影响.
为了观察两种传播方式对疾病控制的影响,分别对仅含大众传播与仅含人际传播的情况进行模拟. 根据文献[5]和[10]中参数取值,取Λ12=0.01,Λ21=0.04,Λ22=0.02,μ1=1/78,μ2=1/70,β11=0.12,β12=0.03,β11=0.14,β12=0.04. 在图2(a) 中,γ1=2/5,γ2=2/6,图2(b) 中,γ1=1/10,γ2=1/12. 图2 中实线代表不含公共卫生教育,虚线代表仅有媒体传播方式,点线代表仅有人际传播方式. 从图中可以看出,实线峰值最高,其次为虚线和点线,表明公共卫生教育的两种措施,都可以降低疾病爆发的峰值,但相对于大众传播,人际传播对疾病峰值的控制更有效,能更好地降低疾病带来的损失.
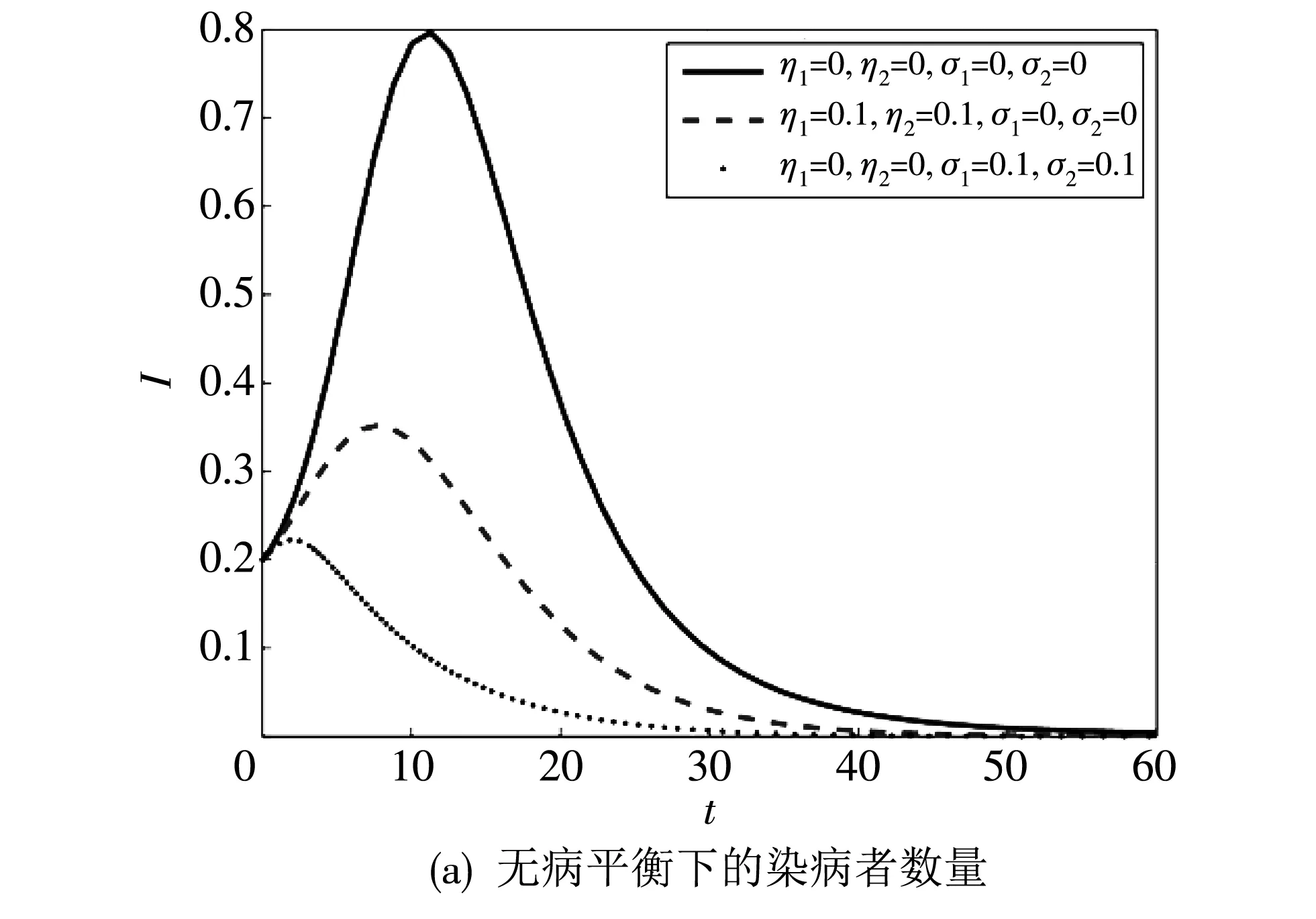
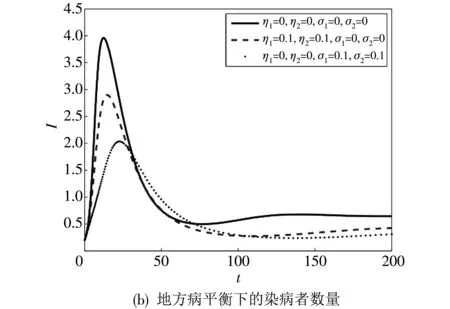
图2 传播方式对疾病峰值的影响Fig.2 The impact of transmission patterns on peak disease
另外,由于一些不可控因素导致信息传播具有一定的滞后性,当疾病爆发后,往往不能及时有效地采取相应的教育防控措施,增加了疾病带来的损失. 令σ1=0.1,η1=0.1,σ2=0.1,η2=0.1,且图3(a)中,γ1=2/5,γ2=2/6,图3(b)中,γ1=1/10,γ2=1/12,其余参数取值不变. 图3 中实线代表不含公共卫生教育,虚线代表在疾病爆发第一天后加入公共教育,点线代表在疾病爆发第五天后加入公共教育. 从图3 可以看出,实线峰值最高,其次为点线和虚线,说明当疾病爆发后,及时的公共卫生教育可以更好地降低疾病爆发的峰值,减少疾病带来的损失.


图3 反应时间对疾病峰值的影响Fig.3 Effect of response time on peak disease
人们通过两种传播方式获得疾病防护的相关知识后,就会有一定的疾病防护能力. 假设bi=βi1-βi2(i=1,2)为人们获得疾病防护信息的正确性,bi>0表示获得正确的疾病防护信息,bi<0表示获得的疾病防护信息是错误的,bi的绝对值表示获得信息正确与错误的程度,令β12=β11-b1,β22=β21-b2,η1=0.006,η2=0.005,σ1=0.006,σ2=0.005,γ1=1/10,γ2=1/12,其余参数不变. 图4 表示平衡状态下染病者的数量随着bi变化的情况,纵轴大小表示染病者人数. 从图中可以看出,随着bi的增加,染病者人数逐渐减小,表明正确的疾病防护信息可以很好地降低疾病的流行程度,相反谣言的传播反而会助长疾病的流行,故我们应注重信息传播的质量,确保信息的准确性,并且应加强谣言的监管.
由于日益频繁的经济交流,人口的流动对疾病传播的影响越来越受重视,接下来对人口迁移对疾病流行程度的影响进行模拟. 令m12和m21变化,其余参数不变. 从图5(a)可以看出,随着m12的增加,染病者数量逐渐增大,随着m21的增加,当m12较小时染病者数量先减少后逐渐增加,但当m12增大到某一值后,随着m21的增加,染病者数量也呈上升趋势,说明第一个斑块向第二个斑块的迁移促进了疾病的传播,而由于第一个斑块的高治疗水平,在一定范围内第二个斑块向第一个斑块的迁移有助于整体疾病的控制,但继续增加后同样会促进疾病的传播. 在图5(b)和图5(c)中可以看到,随着m12的增加,I1逐渐减小,I2逐渐增大,随着m21的增加,I1逐渐增大,I2逐渐减小,表明人口的迁出都有利于本地区疾病的控制,但会加重其他地区的疫情,所以疾病爆发后要尽量减少人口流通.

图4 疾病防护能力对疾病流行的影响Fig.4 The impact of disease protection on disease transmission

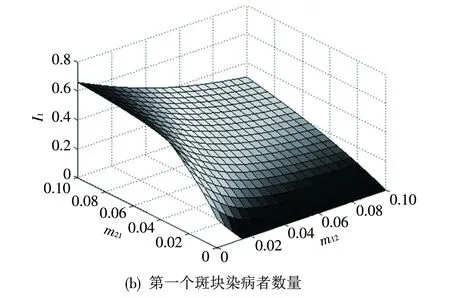
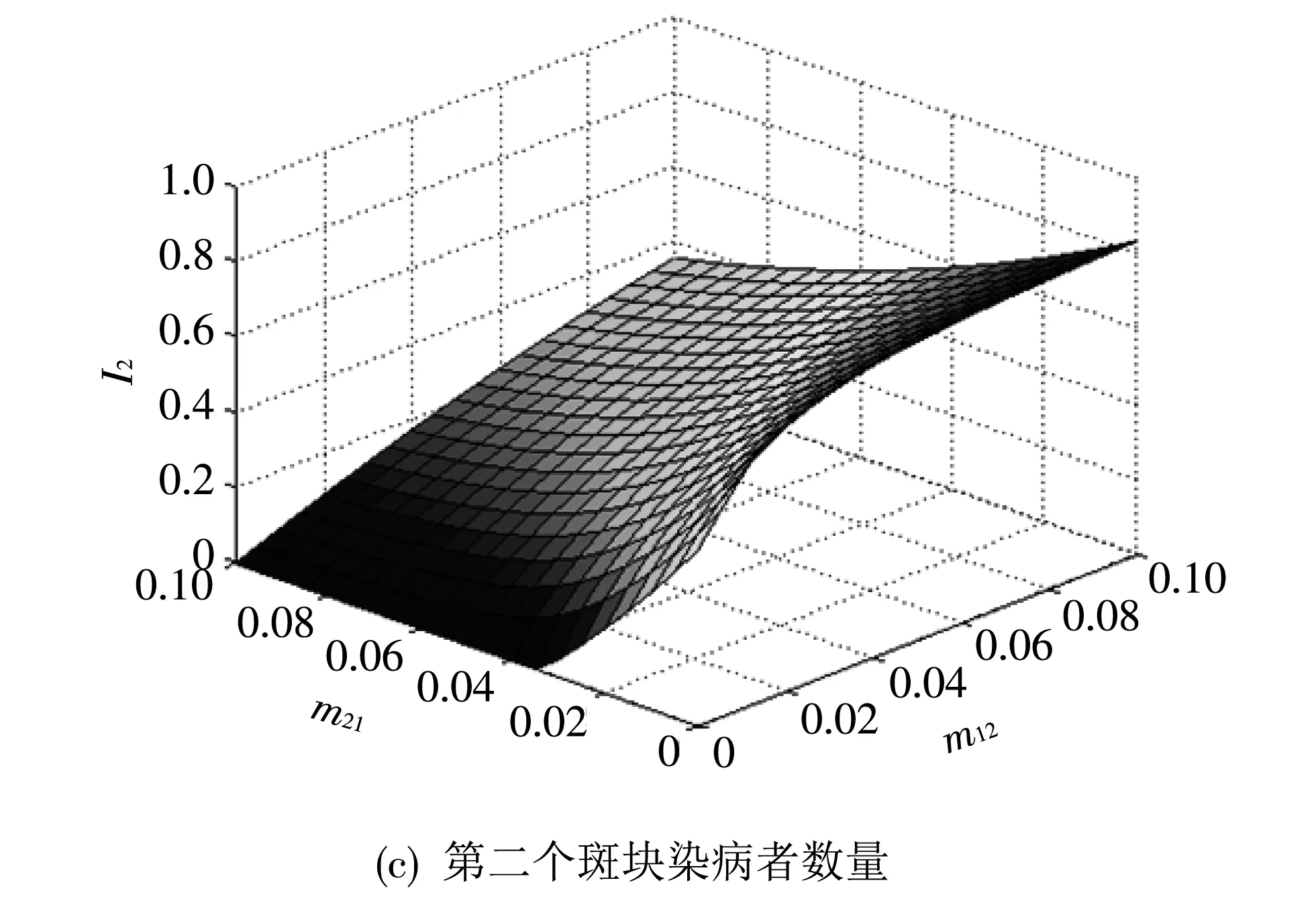
图5 人口迁移对疾病动力学性态的影响Fig.5 Effects of population migration on disease dynamics
3 结 论
本文通过LHS/PRCC和灵敏度指标法,分别对双斑块SIR传染病模型的基本再生数和地方病平衡点进行了敏感性分析,得出各参数对模型性态的敏感程度,之后,通过MATLAB数值分析了各因素对传染病传播的具体影响.
分析结果表明,传染病爆发后,我们应第一时间采取有效的措施,给予大众准确的疾病防护信息,控制谣言的传播,提升人们的疾病防护能力,另一方面,要严格控制人口的流动,防止疾病的扩散,这都可以有效地降低疾病带来的损失,但从本质上来讲,疾病的根除更重要的还是医疗水平的提升.
