基于可靠性方法的山区公路行车安全研究*
2020-04-29蒋愚明
徐 韬 蒋愚明* 陆 键 栗 飞
(同济大学道路与交通工程教育部重点试验室1) 上海 201804) (山西省公路局晋城分局2) 晋城 048000)
0 引 言
传统的道路设计通常参考相应规范来确定某个设计变量的取值,但是无法量化设计值的具体安全水平.可靠性理论作为一种概率分析方法,考虑了各个输入参数的随机性,能够有效克服确定性设计方法存在的不足.国外已经有相当一部分研究将可靠性理论应用于交通安全领域[2-7],主要涉及到道路平曲线、停车视距、中央带设计、超高等.
国内的多数研究大多采用的是专家打分或者事故预测的方法,应用可靠性方法研究交通安全的文献较少.游克思等[8]在国外关于车辆侧滑可靠性研究的基础上,进一步考虑车辆侧倾作用下的侧滑失效模式,并分别构建了基于质点模型与考虑车辆侧倾作用的侧滑失效功能函数,分析了曲线路段的行车安全可靠性.本文选取山西省207国道部分路段作为案例,考虑山区公路车辆行驶的侧滑和视距不足两类失效模式,分别构建功能函数,针对两种失效模式分别进行了失效概率求解和校准,并根据求解结果和弹性分析对相应的道路设计参数给出了参考值.
1 功能函数构建
可靠性是指在一定时间和条件下,系统无故障地执行预期功能的能力.分析的第一步要建立功能函数,在道路安全分析的语境下,供给指某一项道路设计参数的实际取值,需求指车辆安全行驶对于此项设计参数的理论要求.g<0时称系统失效,此时道路设计无法满足车辆安全通行需求,pf=P(g≤0)为失效概率.而供给和需求变量又由其他道路设计参数和交通流参数构成,其中部分参数是确定性的,部分是随机的.因此,安全水平就可以通过计算g>0的概率得到.
g=R-S
(1)
式中:R为供给变量;S为需求变量;g为可靠性指标.
研究表明,在平曲线、纵坡及平纵组合等不良线形路段发生的路侧事故约占总数的59%,不良线形条件对路侧事故的发生有较为明显的诱导作用[9].而在平曲线路段发生的交通事故主要分为两类形态,一种是由于车速过快、路面摩擦系数过小等原因导致车辆打滑冲出路面;另一种是在前方车道有障碍物的突发状况下,由于转弯路段视距不足导致车辆无法及时刹车从而撞向路侧物体.本文分别就这两类事故场景建立功能函数.
1.1 第一类失效场景——侧滑
当车辆以速度V在半径为R的圆曲线上运动时,受离心力作用,产生侧向加速度,有向外运动趋势,速度越大,侧向加速度越大.在一定的路面摩擦系数下,要使车辆能稳定地在曲线路段上行驶而不发生侧滑事故,就需要足够大的半径,此半径即为功能函数中的需求变量,而平曲线半径的设计值即为供给变量.根据牛顿第二运动定律,车辆稳定行驶所需的最小半径为
式中:V为车辆行驶速度;g为重力加速度;e为超高;f为路面侧向摩擦系数.因此,在半径为Rs的平曲线路段,车辆侧滑的可靠性功能函数为
式中:Rs,g,e为确定性变量;V,f为随机变量,其分布情况将在后文详述.
1.2 第二类失效场景——视距不足
车辆在山区平曲线转弯路段行驶时,视线通常会被路侧山体遮挡,因此合理道路设计需要提供足够的可视距离,使得驾驶员在看到前方障碍物时能够及时停车.为使车辆安全通过平曲线路段,道路设计所提供的有效视距ASD(available sight distance)需要大于停车视距SSD(stopping sight distance).根据车辆动力学原理,停车视距SSD的计算方法为
式中:V为汽车行驶速度;T为驾驶员反应时间;g为重力常数;f为路面摩擦系数;i为纵坡坡度,因此,视距不足失效场景的可靠性分析功能函数为
式中:g,i为确定性变量;V,T,f为随机变量,其分布情况将在后文详述.
2 随机变量分布
2.1 行车速度V
传统的交通管理通常采用85分位车速作为运行车速,在可靠性分析中运行车速则是与圆曲线半径和坡度等道路设计参数相关的随机分布.根据Fambro等[10]的研究,正态分布最适合描述车辆在平曲线运行时速度值的分布,因此采用Andjus等[11]对于运行车速分布的研究结论,计算运行速度的平均值Vmean和标准差σ.
Vmean=14.75ln(R)-11.69
σ=0.108 5Vmean+0.99
式中:R为平曲线半径
2.2 摩擦系数f
公路路面所能提供的最大摩擦系数与车辆的运行速度和路面状况密切相关,本文中,潮湿路面下的摩擦系数分布参考Psarianos等[12]的研究,即服从平均值与行车速度线性负相关,而标准差不变的正态分布;而正常干燥路面的摩擦系数则基于Fambro等[13]对车辆制动性能的研究成果,服从正态分布且与行车速度无关,见表1.
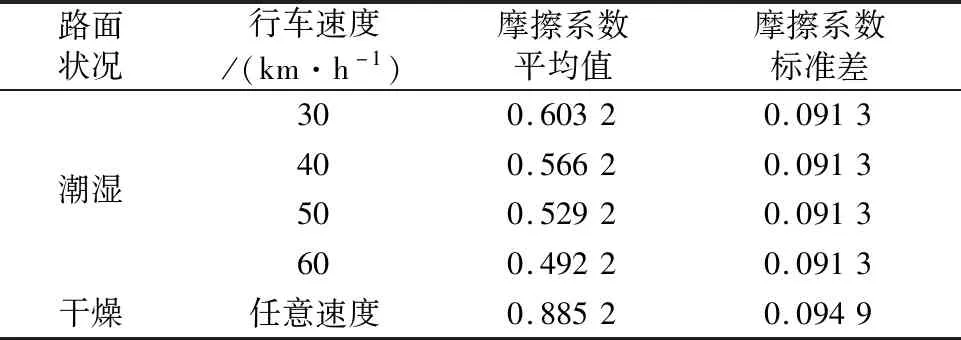
表1 不同路面状况和行车速度下的摩擦系数平均值和标准差
侧滑失效的功能函数需要输入侧向摩擦系数,研究表明,最大侧向摩擦系数是切向摩擦系数的0.925倍,即
fRmax=0.925fTmax
2.3 反应时间T
美国等国的设计标准在计算停车视距时,反应时间一般保守估计取2.5 s[14],代表反应速度较慢的驾驶员.采用Davis等[15]的研究成果,将驾驶员反应时间看作对数正态分布,平均值和标准差分别为1.5和0.4 s,其概率密度函数见图1.
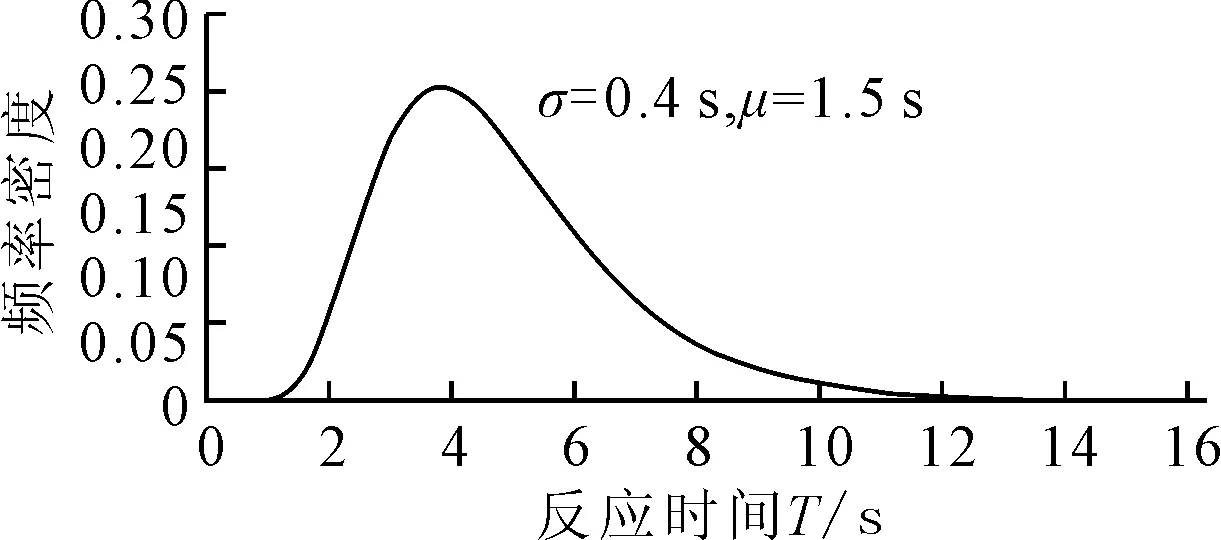
图1 反应时间对数正态分布的概率密度函数
3 可靠性求解
3.1 求解方法选择
在可靠性分析中,简单二元系统的功能函数如下,其失效概率一般可以通过确定性方法,即求联合概率分布函数fR,S(r,s)在失效情况(R≤S)下的积分结果得到.
g(R,S)=R-S
以两个独立正太分布的随机变量为例,功能函数g(R,S)=M=R-S.假设R~N(μR,σR),S~N(μS,σS),可知二者之差M也服从正态分布,其平均值和标准差为
μM=μR-μS
由此,失效概率pf就可以通过标准正态分布的累积分布函数求得

当功能函数g(R,S)涉及到多个随机变量且呈非线性,尤其是随机变量不服从正态分布时,往往很难精确求解,此时可利用近似或模拟方法进行求解.近似求解的方法包括一阶可靠性方法(FORM)和二阶可靠性方法(SORM)等.FORM和SORM方法分别对功能函数在设计点(Design Point)上进行一阶和二阶泰勒展开,因此SORM可以看作是比FORM更加精确的近似求解方法.本文中两类失效函数并不是高度非线性的,且FORM在90%的实际应用场景中都能提供足够的精确度[16].因此本文选择FORM进行求解.
3.2 FORM方法概述
为了求解在多变量系统中的可靠性指数,FORM方法首先将功能函数中的随机变量转换为标准正态分布:
式中:μXi和σXi随机变量Xi的平均值和标准差,此时功能函数中的每个随机变量都被转化为标准正态分布,失效函数也会相应转换.以上文中的二元正态分布系统为例,康奈尔可靠性指数β也可以理解为衡量平均值点(μR,μS)至失效平面R-S=0的一个指标.在转换之后,所示原失效平面R-S=0此时会转化为σRR′-σSS′+μR-μS=0.
图2为失效平面坐标系转换示意图,由图2a)可知,在原始坐标系统中,平均值点(μR,μS)至失效平面R-S=0的距离与康奈尔可靠性指数β线性相关.Madsen等[17]提出了Hasofer-Lind可靠性指数βHL,其定义为原点至失效平面的最短距离.由图2b)可知,此例中βHL就等于转换坐标中原点到失效平面的直线距离.
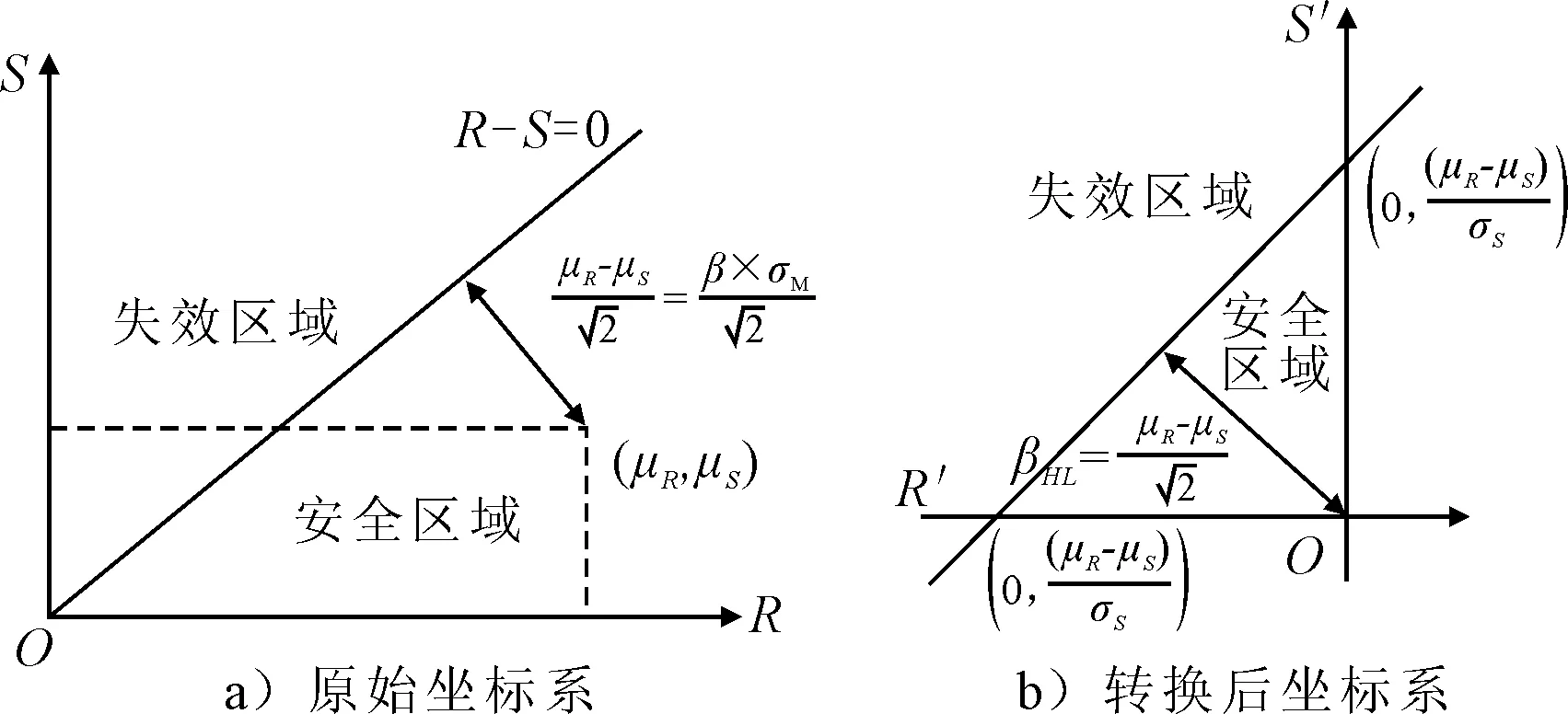
图2 失效平面坐标系转换示意图
此时,问题就转化为求失效平面上一点z*,使得其离坐标原点的距离最短.
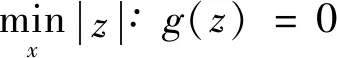
接着将功能函数进行泰勒一阶展开,此过程称作功能函数的线性化:
图3展示了二维空间中功能函数的一阶线性化过程.
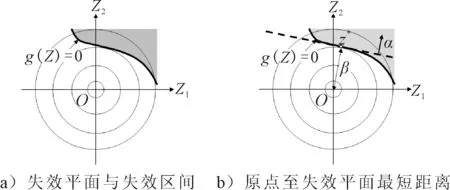
图3 二维空间中功能函数的一阶线性化示意图
通过迭代求得的最短距离βHL,即为系统的可靠性指数,其对应的Φ(βHL)也就是系统的失效概率.
3.3 案例分析
3.3.1侧滑失效
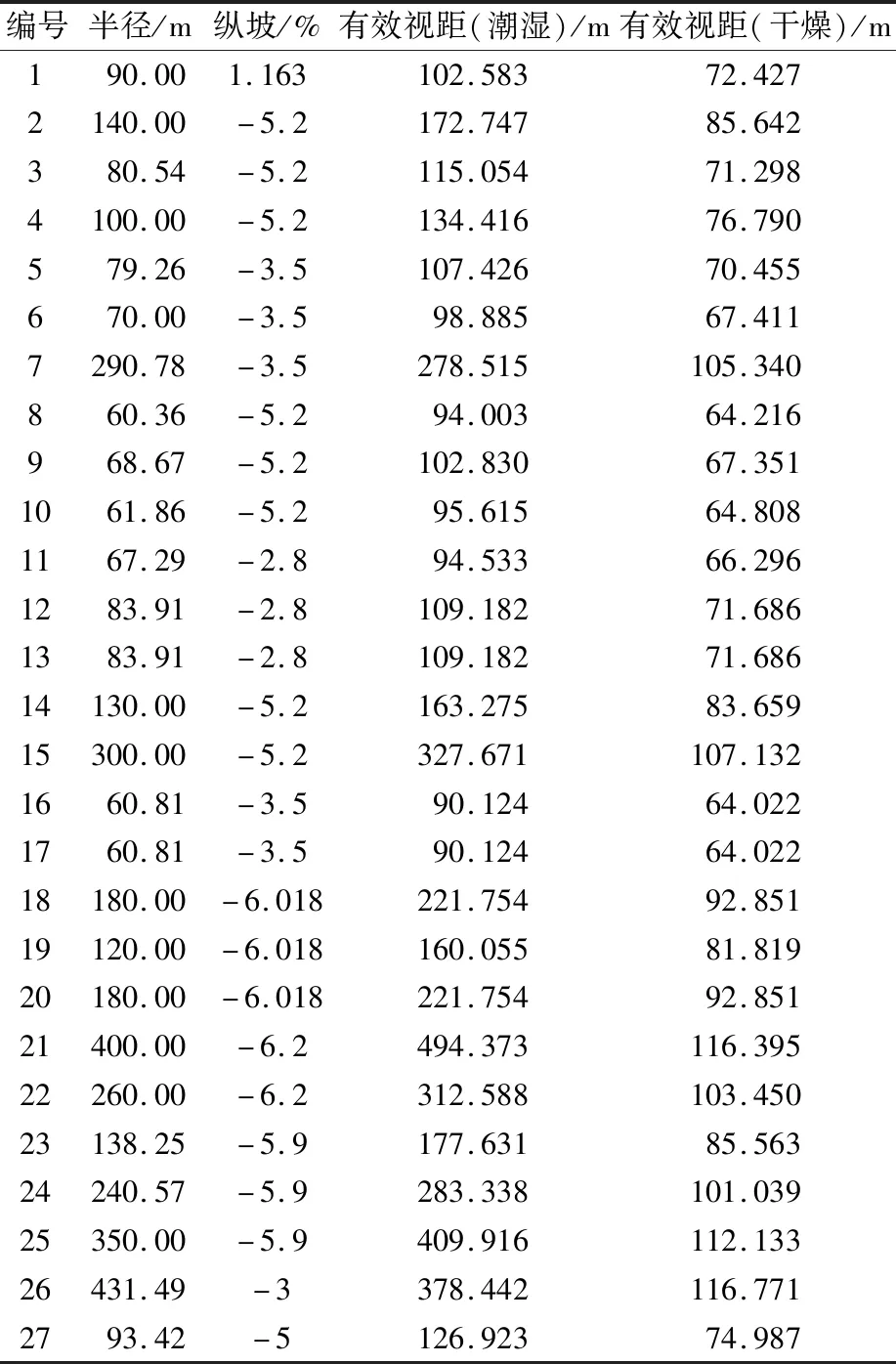
将路段相关数据输入,通过一阶可靠度方法,计算出27个圆曲线路段在干燥路况和潮湿路况下的可靠性指数和侧滑失效概率,见表2.结果显示,干燥路况下汽车在圆曲线路段侧滑失效概率的数量级很小,最大也只有6.56×10-6,而阴雨天气路面潮湿则急剧上升,最高达到3.78%;且侧滑概率较大的都是圆曲线半径较小(60~80 m)的几个路段.

表2 案例路段在干燥和潮湿路况下的可靠性指数和侧滑失效概率
对于新建设的道路,由于半径Rs、超高e和路面摩擦系数f都是定值,因此预防侧滑事故的主要手段是控制车辆在小半径圆曲线路段的行驶速度.为研究小半径曲线不同车速下的侧滑失效概率,此处针对60,65,70,75,80,85,90 m的圆曲线路段,超高设为0.06,计算潮湿路面状况下行车速度平均值从降低10 km/h到增加10 km/h时的侧滑失效概率,结果见图4.由图4可知,总体来说圆曲线半径越小,侧滑概率越大;行车速度均值的少量增加或减少都会引起侧滑失效概率的巨大变化.
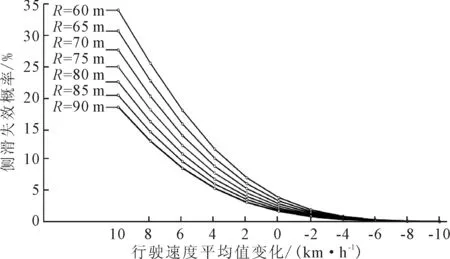
图4 不同圆曲线半径条件下加减速度平均值的侧滑概率
3.3.2视距不足失效
由于客观条件限制,圆曲线可提供的有效视距ASD无法获取.因而此处采取可靠性校准的方法,首先确定一个目标失效概率pt,再通过数值优化计算出案例路段各个圆曲线需要满足的最小视距ASD,使得视距不足的失效概率低于pt.
minASD∶P(g(ASD)≤0) 在确定目标失效概率pt之前,需要探究一定线形条件和路面状况下,失效概率与有效视距ASD的关系.此处选取半径为60,80,120,180,260,350 m的圆曲线路段,假设纵坡坡度为下坡6%,分别研究其在干燥和潮湿路面状况下,失效概率随着有效视距变化的情况,计算结果见图5.由图5可知,相同路面状况和有效视距下,圆曲线半径越大,失效概率越大.此结论看似与"小半径曲线更危险"的常识相冲突,实则因为功能函数的模型假设中行车速度随着曲线半径增大而增大,所以大半径圆曲线所需要的有效视距也就越大.且在同样的半径和有效视距下,潮湿路面的失效概率远大于干燥路面. 总体来说,对于干燥路面,将有效视距设置在100 m就可以将各个圆曲线半径的视距不足概率控制在1%以下;而多数情况下,要到达到较低的失效概率,潮湿路面所需要的有效视距则要大于100 m. 图5 不同半径圆曲线的视距不足失效概率随有效视距的变化 本文将目标失效概率pt设为0.1%,计算案例路段所需要的有效视距,以供相关道路建设部门参考.问题转化为求有效视距ASD,使得视距不足的失效概率为0.1%,即: ASD∶g(ASD)=0.001 此为标量函数求根问题,可采用的算法有布伦特算法(Brent)、二分法等.本文采用布伦特算法[18],取值范围设定为0~1 000 m,求出案例路段在干燥和潮湿路面状况下所需要的最小视距,结果见表3.由表3可知,潮湿路面所需要的最小视距远大于干燥路面,且其差值随着半径的增大而增加.建议相关部门结合当地气候状况,在特定路段制定合适的有效视距. 表3 27个圆曲线路段的最小视距 值得一提的是,即视距不足的失效概率并不等同于事故概率.视距不足所导致的事故是建立在圆曲线路段前方存在障碍物的前提下,因而此处的失效概率(0.1%)也是较为保守和安全的设计. 1) 干燥路况下车辆在案例路段的侧滑失效概率很小,阴雨天气路面湿滑时则显著上升,且圆曲线半径越小,侧滑概率越高. 2) 控制车速是避免车辆侧滑的有效途径,在各个半径条件下,将行车速度均值降低4 km/h都可以将侧滑概率降至1%以下. 3) 潮湿路面的视距不足失效概率同样远大于干燥路面.干燥路面上将视距设置在100 m时,各个半径条件的圆曲线视距不足概率都会降至1%以下;而多数情况下,要到达到较低的失效概率,潮湿路面所需要的有效视距则要大于100 m.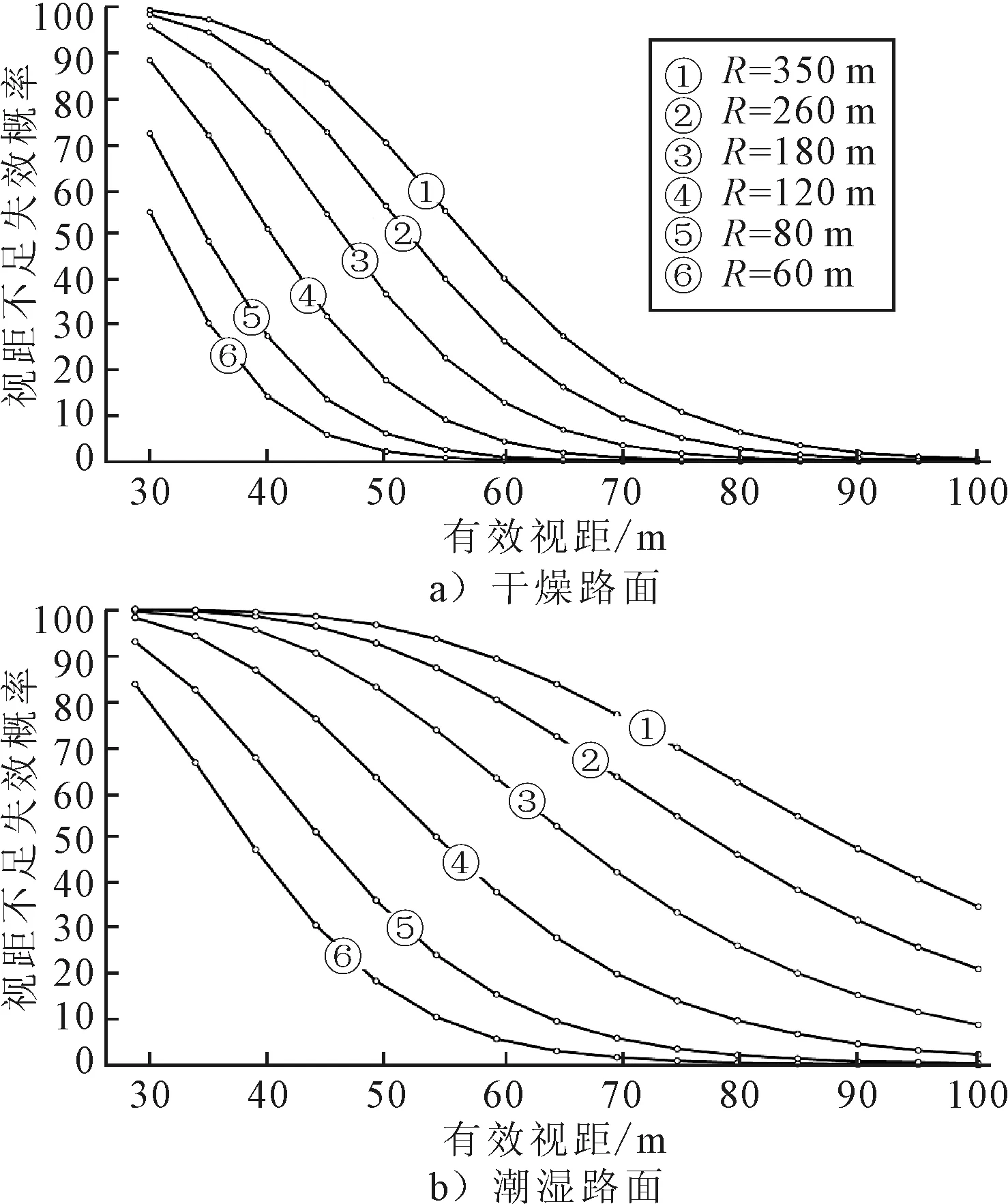
4 结束语
