新弱化缓冲算子的构造及其优化

王 安,杨 雨，惠志昊，甘荣浩

(1.平顶山学院 数学与统计学院，河南 平顶山 467036；2.平顶山学院 计算机学院，河南 平顶山 467036)

灰色预测模型是通过对样本数据的挖掘，构造累加序列，利用微分方程的差分近似建立起来的数学模型.自邓聚龙教授建立灰色理论以来，灰色理论迅速在很多领域得到应用，成功地解决了大量的预测问题.灰色预测模型与其他预测模型的不同之处在于对样本数据的要求和处理不同，一个平稳的时间序列，灰色预测模模型很容易得到高精度的预测结果.如果平稳的时间序列受到某种干扰，可能预测结果的误差较大.因此如何减弱冲击干扰的影响，挖掘事物内部发展的规律，是人们研究的一个重要问题.

弱化算子可以减弱冲击干扰的影响，很快在多个领域得到了应用[1-3]，并出现了很多的改进形式[4-7].但是传统的弱化算子大多是固定结构的，利用优化的弱化算子预测的文献还不多见.笔者基于微积分的思想和微分的不同差分格式，构造了一种新的弱化算子，根据最小二乘法原理给出了最优弱化算子的计算方法.

1 灰色系统的一些基本理论

公理1[8](不动点公理)若X={x(1),x(2),…,x(n)}为系统行为数据序列,XD={x(1)d,x(2)d,…,x(n)d}为序列算子,则D满足x(n)d=x(n).

不动点公理限定在序列算子作用下,系统行为数据序列中的数据x(n)保持不变,即用序列算子对系统行为数据进行调整时,不会改变x(n).

公理2[8](信息充分利用公理)系统行为数据序列X中的每个数据x(n)都应充分参与算子作用的全过程.

信息充分利用公理限定任何序列算子都应以现有序列中的信息为基础进行定义,不允许抛开原始数据序列.

公理3[8](解析化、规范化公理)任意的x(k)d都可由一个统一的x(i)初等解析式表达.

定理1[8]X={x(1),x(2),…,x(n)},XD={x(1)d,x(2)d,…,x(n)d}分别为单调递增长序列和缓冲序列，有：D为弱化算子⟺x(k)d≥x(k),k=1,2,…,n，D为强化算子⟺x(k)d≤x(k),k=1,2,…,n.

定理2[8]X={x(1),x(2),…,x(n)}，XD={x(1)d,x(2)d,…,x(n)d}分别为单调递衰减序列和缓冲序列，有：D为弱化算子⟺x(k)d≤x(k),k=1,2,…,n,D为强化算子⟺x(k)d≥x(k),k=1,2,…,n.

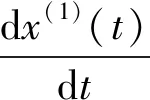
(1)

方程(2)称为GM(1,1)模型的时间响应函数:

(2)

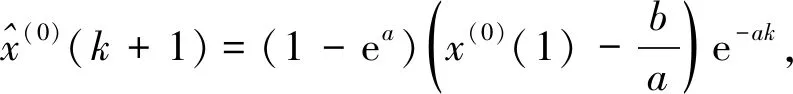
(3)

由上述定义可知，GM(1,1)模型是对数据累加序列呈指数增长的近似模拟，会有好的预测结果.但是在自然界中，很多研究对象并不是累加呈指数增长的，所以导致预测误差太大.基于此，笔者构造了一类新的弱化算子，通过弱化算子的作用，改进GM(1,1)模型的预测效果.

2 一类新的弱化算子的构造

定理4 设X={x(1),x(2),…,x(n)}为非负原始数据，其缓冲算子XD1={x(1)d1,x(2)d1,…,x(n)d1}，其中：x(k)d1=λx(k)+(1-λ)x(k+1),λ∈[0,1]，k=1,2,…,n-1,x(n)d1=x(n).则当X为增长序列、衰减序列或震荡序列时，缓冲算子XD为弱化算子.

证明易证D1满足缓冲算子三公理，因而D1为缓冲算子.

当X为增长序列时，由于x(k)d1=λx(k)+(1-λ)x(k+1)≥(λ+(1-λ))x(k)=x(k)，则有X(k)d1≥x(k)，所以当X为增长序列时，D为弱化算子.

同理可证当X为衰减序列时，D为弱化算子.

当X为震荡序列时，设x(i)=max{x(k)|k=1,2,…,n}，由于x(i)d1=λx(i)+(1-λ)x(i+1)≤λx(i)+(1-λ)x(i)=x(i)，则有x(i)d1≤x(i)，所以

设x(j)=min{x(k)|k=1,2,…,n}.由于

x(j)d1=λx(j)+(1-λ)x(j+1)≤λx(j)+(1-λ)x(j)=x(j)，x(j)d1≤x(j)，

所以当X为震荡序列时，D为弱化算子.

3 最优弱化算子的确定

由导数的定义知

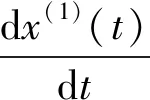
(4)

这种新的差分格式正是我们构造的新的弱化算子.

于是,经过弱化算子作用后的GM(1,1)模型如下：

λx(0)(t)+(1-λ)x(0)(t+1)+az(1)(t)=b,t=2,3,…,n,….

(5)

其中a为发展系数，b为灰色作用量，λ为弱化算子的优化参数.

记u=[a,b,λ]T，Y=[x(0)(3),x(0)(4),…,x(0)(n)]T，

则弱化算子作用后的GM(1,1)模型可表示为:

Y=Bu.

(6)

其中，

令J(u)=(Y-Bu)T(Y-Bu),则

利用最小二乘法，使得J(u)=(Y-Bu)T(Y-Bu)取得最小值，则有

得到参数的最优估计：

(7)

(8)

最优弱化算子模型的时间响应函数为：

(9)

利用

(10)

得到预测值序列：

(11)

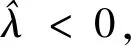
4 模型检验

利用平均绝对误差检验模型的准确性，其定义如下：

(12)

利用平均绝对误差检验模型的模型精度，常用的模型精度等级检验表[10]如表1所示.

表1 模型精度等级检验表

k时刻的相对误差,其定义如下[11]：

(13)

5 算例分析

根据2016年中国统计年鉴中中国能源生产总量和消费总量数据，用MATLAB做出中国2001—2015年期间能源总量生产和消费趋势图，如图1所示.

图1 2011—2015年中国能源生产总量 和能源消费总量变化趋势

由图1可知，中国能源生产总量和消费总量在2001—2015年期间呈逐年增长趋势，中国能源生产总量增长的速度低于中国能源消费增长的速度，并且两者之间的差距越来越大，这说明中国能源消费的自给能力越来越差.

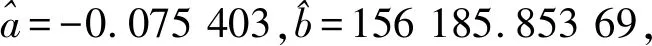
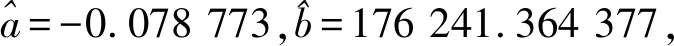
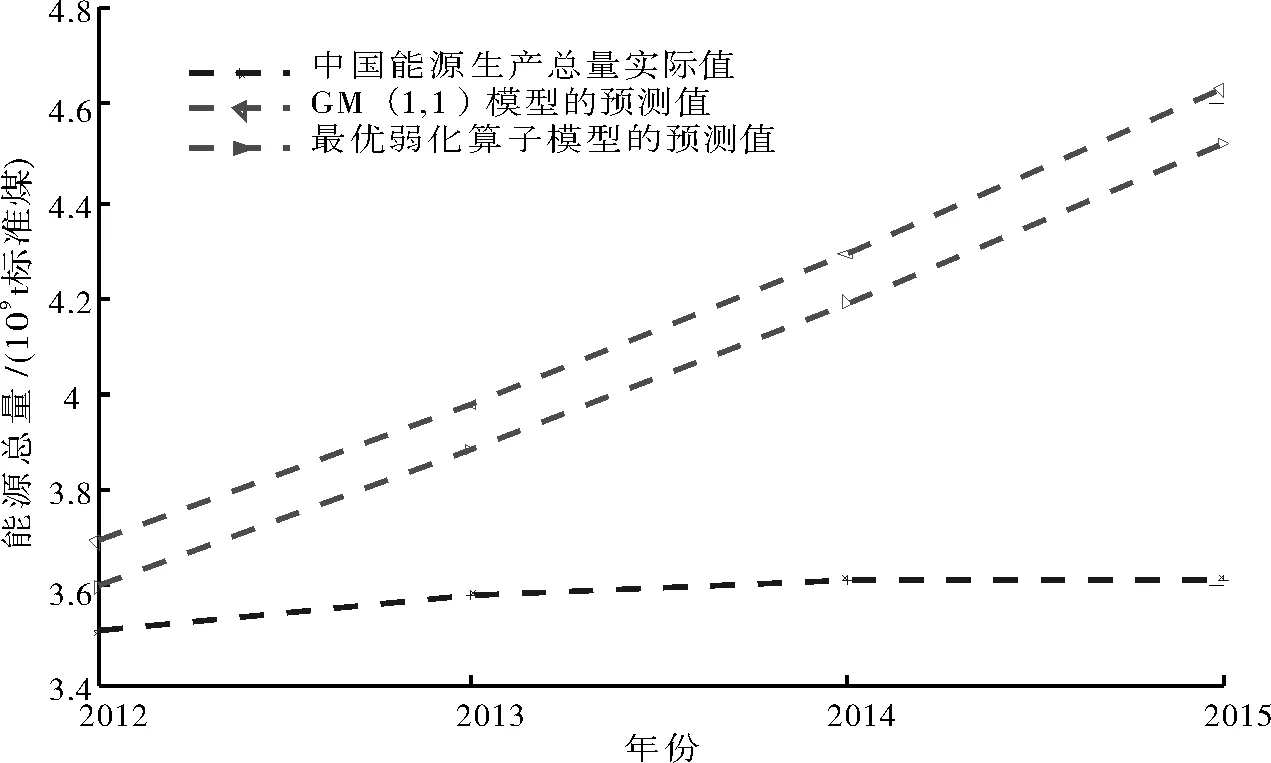
图2 2012—2015年中国能源生产总量的真实值与 GM(1,1)模型和最优弱化算子模型预测值对比

图3 中国能源生产总量GM(1,1)模型和 最优弱化算子模型预测值的相对误差对比

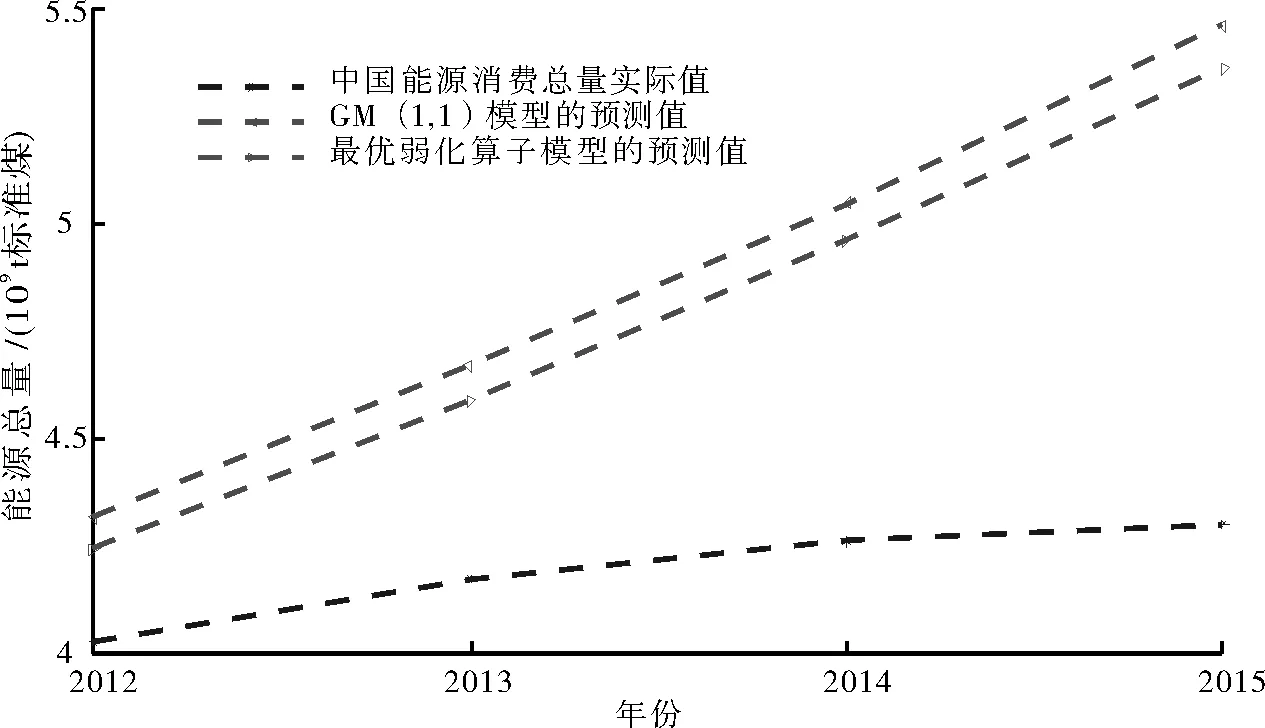
图4 2012—2015年中国能源消费总量的真实值与 GM(1,1)模型和最优弱化算子模型预测值对比

6 结论

笔者构造了一种新的弱化算子，并给出给予最小二乘法的最优弱化算子求解办法，通过算例发现，相对于传统的GM(1,1)模型，最优弱化算子模型的预测结果与真实数据更接近，精度明显提高，该方法是对GM(1,1) 模型的拓展．对解决各个领域中普遍存在的灰色累加序列非指数增长的建模拟合和预测问题具有广泛的应用价值．

图5 中国能源消费总量GM(1,1)模型和 最优弱化算子模型预测值的相对误差对比