广义时滞系统的稳定性条件

于姗姗

(沈阳师范大学 数学与系统科学学院，辽宁 沈阳 110034)

0 引言

时滞现象在实际系统中是普遍存在的，时滞的存在通常会造成系统不稳定，影响系统的整体性能.在各类工业系统中都含有时滞，例如:涡轮喷气式飞机、核反应堆、轮船定向仪、无损耗传输系统等.时滞系统稳定性的研究取得了大量研究成果[1-8].

广义系统是一类形式更一般化，比正常系统更具有广泛形式和应用背景的动力系统[9-15].20世纪70年代广义系统的理论被提出，许多正常系统的结论被相继地推广到广义系统中.系统奇异矩阵的存在会使系统产生脉冲，可能造成系统瞬间崩溃，这是研究广义系统稳定性必须考虑的问题.因此，研究连续广义系统的稳定性，首先要保证系统的正则性和无脉冲性，再考虑稳定性.

通过适当的模型变换，利用中立系统变换方法来处理广义时滞系统，为求得广义时滞系统稳定性提供了新方法[12-14].文献[12-13]提出将广义时滞系统转化为中立时滞系统，进而研究了广义时滞系统的稳定性问题.文献[14]也通过此模型变换，利用自由矩阵积分不等式，处理了广义时滞系统的稳定性问题，减小了结果的保守性.

在研究时滞系统稳定性条件的过程中，较为常用的方法是L-K泛函法，比如引入三重积分项到L-K泛函[12-13]、增广的L-K泛函[14-15]等.在处理泛函产生的积分项上，应用积分不等式方法较为广泛，对于处理泛函导数中的一重积分项，由Jensen积分不等式[1]发展到了Wirtinger积分不等式[2]，辅助函数积分不等式[3]，进而又用到B-L积分不等式[4].与前3个积分不等式相比，B-L积分不等式的保守性更小，具体说明见文献[4].

笔者通过中立模型转换法，将广义时滞系统转化为等价的中立时滞系统.提出增广的L-K泛函，然后对泛函求导，利用四阶B-L积分不等式更精确地对求导后的积分项进行放大，得到保守性更小的中立时滞系统稳定性充分条件，进而得到广义时滞系统的稳定性充分条件.最后，两个数值算例表明笔者所获得方法的有效性和优越性.

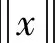
1 问题描述

考虑如下连续广义时滞系统：

(1)

其中，x(t)∈Rn为系统状态向量，Rn是定义在实数域上的n维向量空间，h>0表示定常时滞，φ(t)∈R是连续的向量值初始函数.矩阵E∈Rn×n，且rankE=r≤n.A,Ad为已知适当维数的常数矩阵.

定义1[9]若det(sE-A)≠0,则称矩阵对(E,A)是正则的;若deg det(sE-A)=rank(E),则称矩阵对(E,A)是无脉冲的.

定义2[11]若矩阵对(E,A)是正则、无脉冲的，则称广义时滞系统(1)是正则、无脉冲的.

引理1[9]如果矩阵对(E,A)是正则、无脉冲的，则存在两个非奇异矩阵M∈Rn×n和N∈Rn×n使得下式成立：

其中矩阵A1∈Rr×r.

首先将系统(1)转化成一定约束下的中立型系统.根据引理1，如果(E,A)是正则、无脉冲的，一定存在两个非奇异矩阵M∈Rn×n和N∈Rn×n，使得

(2)

(3)

其中(3)中矩阵分块与(2)中矩阵分块方式相一致.u1(t)、u1(t-h)为r维列向量，u2(t)、u2(t-h)为n-r维列向量.所以，系统(1)等价于

即

(4)

0=u2(t)+Ad3u1(t-h)+Ad4u2(t-h) .

(5)

对(5)求导，可得

(6)

联立(5)和(6)，得

(7)

联立(4)和(7)，得

系统(1)可表述成如下的形式:

(8)

其中

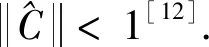
引理2[11]如果矩阵对(E,A)是正则、无脉冲的，系统(1)是无脉冲的并且解存在,且在[0,∞).

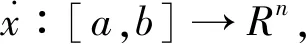
其中:

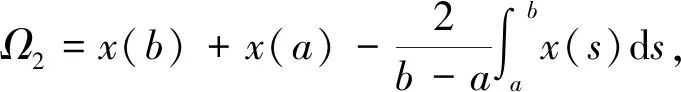
2 主要结果

定理1 对于给定参数h>0，系统(6)是稳定的.若存在正定矩阵P∈R6n×6n，正定矩阵Q，R，S∈Rn×n，满足下面线性矩阵不等式

Φ=sym{ΓT1PΓ2}+eT1Qe1-eT3Qe3+eT0Re0-eT2Re2+h2eT0Se0-ΓT3SΓ3- 3ΓT4sΓ4-5ΓT5SΓ5-7ΓT6SΓ6-9ΓT7SΓ7<0 .

(9)

其中:

证明为系统(8)选择如下形式的L-K函数:

V(u(t))=V1(u(t))+V2(u(t))+V3(u(t))+V4(u(t)) ,

为了方便记

沿着系统(8)，关于t对V(u(t))求导数，得

(10)

(11)

(12)

即

(13)

根据(10)～(13),整理得

(14)

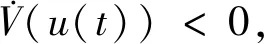
注释1 在处理广义时滞的稳定性时，常出现半正定项ETSE，使得稳定性条件难以表述成严格的线性矩阵不等式形式.中立系统变换方法避免了这个问题，为获得广义时滞系统的稳定性条件提供了新思路.

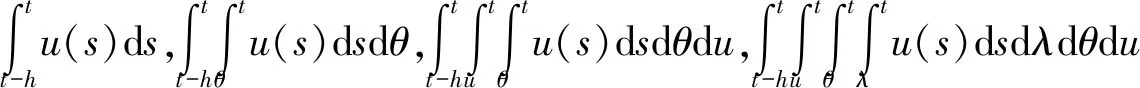
3 数值算例

本节用2个数值例子来说明本文方法的有效性和优越性.

例1 考虑如下广义时滞系统[16]：

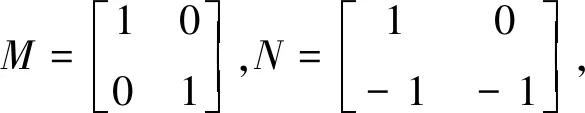
根据定理1，得

例2 考虑如下中立型时滞系统[8]：

其中，c为参数.利用定理1，并用MATLAB的LMI工具箱求解，通过2个数值例子算出系统允许最大时滞hmax，与已有文献相比的结果分别列在表1、表2中，可以看出，本文方法具有更小的保守性.

表1 比较广义时滞系统允许最大时滞hmax

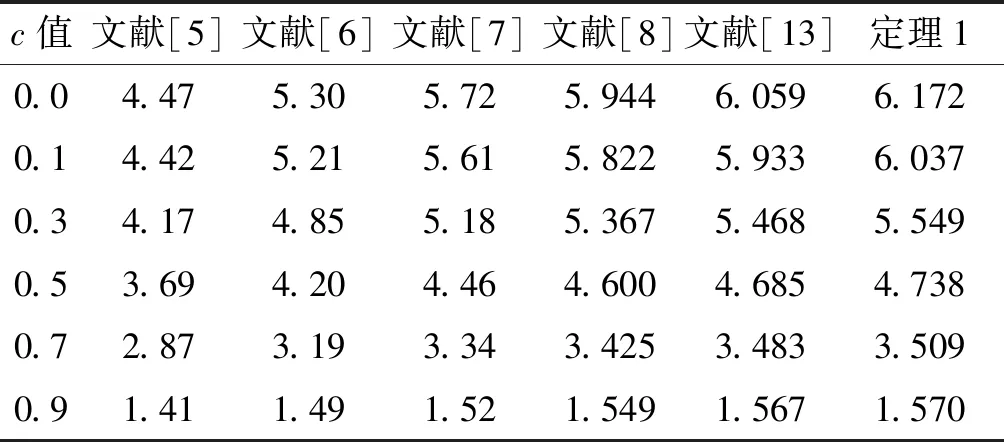
表2 比较中立时滞系统允许最大时滞hmax

4 结论

笔者利用中立系统变换方法，研究了广义时滞系统的稳定性问题.选取了增广的L-K泛函，在处理积分项时利用了B-L积分不等式，给出了新的稳定性条件判据.而在文献[12]和[13]中，采用了Wirtinger积分不等式(具体见文献[2])来处理求导后积分项，相比之下，笔者采取的四阶B-L积分不等式更能精确地对求导后积分项进行放大，因此，该方法适当地降低了保守性.最后用2个数值例子表明，此方法在处理广义时滞系统和中立时滞系统的稳定性上，更具有优越性.