港口供应链中分配公平关切和对等公平关切对订单分配的影响

陈东辉 张桂涛

摘要：为研究港口供应链中公平关切对订单分配的影响，针对由一个港口企业与两个依次参与分配竞争的港口业务服务商组成的二级港口供应链，构建考虑分配公平关切和对等公平关切的博弈模型。运用博弈论分析公平关切对港口供应链订单分配的影响。研究表明：港口企业的最优效用会随第二个港口业务服务商的对等公平关切增加，随当前港口业务服务商的分配公平关切减少。港口企业期望港口业务服务商具有更多的对等公平关切和较少的分配公平关切，故提出一种协调机制，当参数满足一定条件时可以提高港口企业的效用。

关键词： 港口供应链; 订单分配; 分配公平关切; 对等公平关切; 博弈论

Abstract： In order to study the impact of fairness concern on order allocation in port supply chains， a game model considering the distributional fairness concern and the equal fairness concern is built for a two-stage port supply chain consisting of one port enterprise and two port service providers participating in the distribution competition in turn. The game theory is used to analyze the impact of fairness concerns on order allocation of port supply chains. The study finds that， the optimal utility of the port enterprise increases with the equal fairness concern of the second port service provider， and decreases with the distributional fairness concern of the current port service provider. As the port enterprise expects port service providers to have more equal fairness concern and less distributional fairness concern， a coordination mechanism is proposed to improve the utility of the port enterprise when parameters meet certain conditions.

Key words： port supply chain; order allocation; distributional fairness concern; equal fairness concern; game theory

0 引 言

港口是连接内陆和海洋的重要枢纽。最近的数据表明：按重量计算，2018年海运贸易量占世界贸易总量的80%;按价值计算，海运贸易所占份额超过70%。海运贸易的发展取决于货物来源地与目的地港口之间的协调，以及服务和代理人（托运人、港口经营人、货运代理和承运人）的内部协调[1]。越来越多的港口企业选择将其订单外包给港口业务服务商，从而形成更好地满足客户需求的港口服务供应链。合理的訂单分配是维护供应链合作关系的基石[2]。因此，对港口供应链来说，制定合理的订单分配协调机制至关重要。

陆永明[3]的分析表明，无论港口物流服务需求是否具有价格敏感性，实施利益共享契约的协调机制都可以实现Pareto改进。严南南等[4]通过算例验证表明：收益共享契约下的港口供应链协调能够产生更大的经济效益，实现收益共享。高洁等[5]认为港口企业整合物流服务供应商，构建自身的供应链是今后港口的发展趋势。杨波峰[6]研究了基于政府补贴的协调机制，对公平中性、陆运承运人以航运承运人为参考点存在公平关切、航运承运人以港口为参考点存在公平关切3种情况，分别给出了补贴的最小临界值。真虹[7]认为港口运营商应营造出一个敏捷化的港口，顺利跨入第四代港口的行列。邵万清[8]认为在非对称信息条件下，利用期权契约可以实现港口服务供应链的协调。孟丽君等[9]认为对于由物流服务集成商主导的物流服务供应链来说，收益共享契约的协调作用与批发价格契约的协调作用相同。BUSSE[10]认为服务供应商的创新支持水平对于自身发展至关重要，这有助于服务供应商的有效竞争。FEHR等[11]认为公平关切对决策者的效用和供应链的渠道伙伴关系有显著影响。HO等[12]认为在订单分配决策问题中，参考点可以在垂直或水平供应链中选择，分别引起分配公平关切和对等公平关切。陈俊霖等[13]的研究表明，供应链是一个复杂的网络结构，供应链成员除了纵向比较外，还将同行竞争者作为参照点进行横向比较，引起对等公平关切。

以上研究表明，港口供应链的研究已经成为近几年学者们研究的热点。部分学者运用博弈论方法研究了公平关切对港口供应链协调机制的影响，很少有学者注意到两种类型的公平关切对港口供应链订单分配的影响。港口供应链因港口地理位置特殊性而与一般的物流服务供应链不同，合理的订单分配至关重要。然而，在实际情况中港口企业与港口业务服务商之间的利益分配、不同的港口业务服务商之间的订单分配并不均衡，影响了港口供应链的效用。因此，与以往的研究不同，本文对两个同级服务商之间的竞争关系和决策顺序进行建模，在Stackelberg博弈模型中引入分配公平关切和对等公平关切。当前的港口业务服务商表现出分配公平关切，新参与的港口业务服务商表现出对等公平关切。这两种类型的公平关切在参照点方面存在差异，影响订单分配决策[14]。同时，本文提出一种协调机制（成员费和利润分配的协调机制），以最大化港口企业的效用，实现港口供应链的决策优化。

1 模型描述与构建

在现有研究的基础上，本文提出一个由两个港口业务服务商为一个港口企业提供同质化服务的模型。已经有研究[15]表明，创新支持的投资可以提高服务质量和客户满意度，并且增加需求。在实际情况中，订单分配是由港口企业的分配机制决定的，它取决于港口业务服务商的创新支持水平。随着创新支持水平的提高，港口业务服务商可以争取更多的订单。需求函数可以表述为Di=α-p+ei，其中：α表示每个港口业务服务商的潜在需求量;p表示单位物流服务零售价格;ei表示港口业务服务商i（i=1，2）的创新支持水平。[16-17]港口企业决定统一零售价格p，以批发价格w向港口业务服务商购买物流服务。为保证单位利润水平的稳定，p与w存在一定的关系，即p=ηw[18]，其中η是价格系数，η≥1，w不是港口业务服务商的决策变量，而是由零售价格p决定的。在实际情况中，服务供应商通常是跟随者，不能控制批发价格。例如，洋浦港作为港口物流服务集成商，有36个码头作为其服务供应商。为避免各服务供应商因批发价格不同产生纠纷，洋浦港为所有的服务供应商提供统一的批发价格。在本文的基本模型中，假设无论是当前的港口业务服务商还是新参与的港口业务服务商，它们与港口企业的批发价格是相同的，每个港口业务服务商都将努力提高其创新支持水平，以吸引更多的潜在订单。港口企业作为Stackelberg博弈的领导者，首先决定零售价格p，然后由当前的港口业务服务商决定其创新支持水平e1。另外一个港口业务服务商作为新参与者，在观察了当前港口业务服务商的决策后，决定其创新支持水平e2。基于此，本文构建了不同决策序列下的港口供应链模型，见图1。

在港口供应链中，港口企业总是具有更强的控制能力。一方面，许多学者已经表明，领导者可以获得更多的渠道利润[19];另一方面，港口企业也可以通过改变供应链的规则保护自己。例如2012年，营口港为追求利润增长，改变了与服务供应商的利润分配规则。因此，本文不考虑港口企业的公平关切，其公平关切只影响两个港口业务服务商的决策。港口业务服务商1较早进入市场，且不清楚港口业务服务商2的信息，因此表现出分配公平关切;当港口业务服务商2进入市场时，利益分享协调机制已经确定，因此它更注重横向比较，并表现出对等公平关切。港口业务服务商i的效用函数将受到公平关切的影响，即USi=πSi+Si（ei，p），其中：πSi表示港口业务服务商i的利润;Si（ei，p）表示与公平关切相关的效用，Si（ei，p）=-λimax（πr-πSi，0）-βimax（πSi-πr，0），其中下标r表示参考点，λi代表劣势公平关切系数，βi代表优势公平关切系数。λi和βi越大，公平关切的影响就越大。劣势不公平性对决策者的影响更突出[20]，因此为便于在基本模型中进行分析，本文只讨论劣势不公平性，Si（ei，p）的表达可以简化为Si（ei，p）=-λi（πr-πSi）。

1.1 模型参数

其他模型参数：ci为港口业务服务商i的运行成本;r′为港口企业的净利润率;η为价格系数，η=1+r′;k为港口业务服务商的创新成本系数;θ为港口业务服务商之间创新支持水平的横向竞争系数;qi为分配给港口业务服务商i的订单数量;λ1为港口业务服务商1的分配公平关切系数;λ2为港口业务服务商2的对等公平关切系数;πP为港口企业的利润函数;S1（e1，p）为港口业务服务商1与分配公平关切相关的效用;S2（e2，p）为港口业务服务商2与对等公平關切相关的效用;UP为港口企业的效用函数;ρ为分配公平关切与对等公平关切的相对强度;μ为港口业务服务商向港口企业支付的成员费;β为协调机制中港口企业决定的利润分享率;*为决策变量的最优值标志;顶部加“·”的变量值为协调机制作用下的决策变量值。

FD表示港口业务服务商1具有分配公平关切，港口业务服务商2具有对等公平关切;FN表示港口业务服务商1具有分配公平关切，港口业务服务商2为公平中性;ND表示港口业务服务商1为公平中性，港口业务服务商2具有对等公平关切;NN表示两个港口业务服务商都是公平中性的。

1.2 模型假设

（1）订单分配数量与港口业务服务商的竞争有关，其公式为qi=α-p+ei+θ（ei-ej）[18]。θ越大，创新支持水平差异的影响就越大。参数满足2（1+λ）（kη-1-θ）+λ（η-1-θ）>2β（η-1）。[18]

（2）每个港口业务服务商创新总成本为ke2i/2[21]。

（3）两种公平关切的边际效用是相等的，即λ1=λ2=λ。[22]

1.3 模型建立

1.3.1 FD模型

首先考虑两种类型公平关切都存在的情况。当前港口业务服务商侧重于分配公平关切的纵向比较，新参与的港口业务服务商侧重于对等公平关切的横向比较。

1.3.2 FD模型的特殊情况

讨论FD模型的3种特殊情况。由于港口业务服务商与港口企业的信息不对称，在实际情况中很难确定港口业务服务商的公平关切类型。假设港口企业是公平中立的，考虑港口业务服务商1是否具有分配公平关切，考虑港口业务服务商2是否具有对等公平关切。建立FN模型、ND模型和NN模型分别对应公平关切的不同组合。

为保证效用函数是凹函数，参数应该满足假设（1）提到的2（1+λ）（kη-1-θ）+λ（η-1-θ）>2β（η-1）。

1.4 模型分析

1.4.1 港口企业的最优定价和最优效用

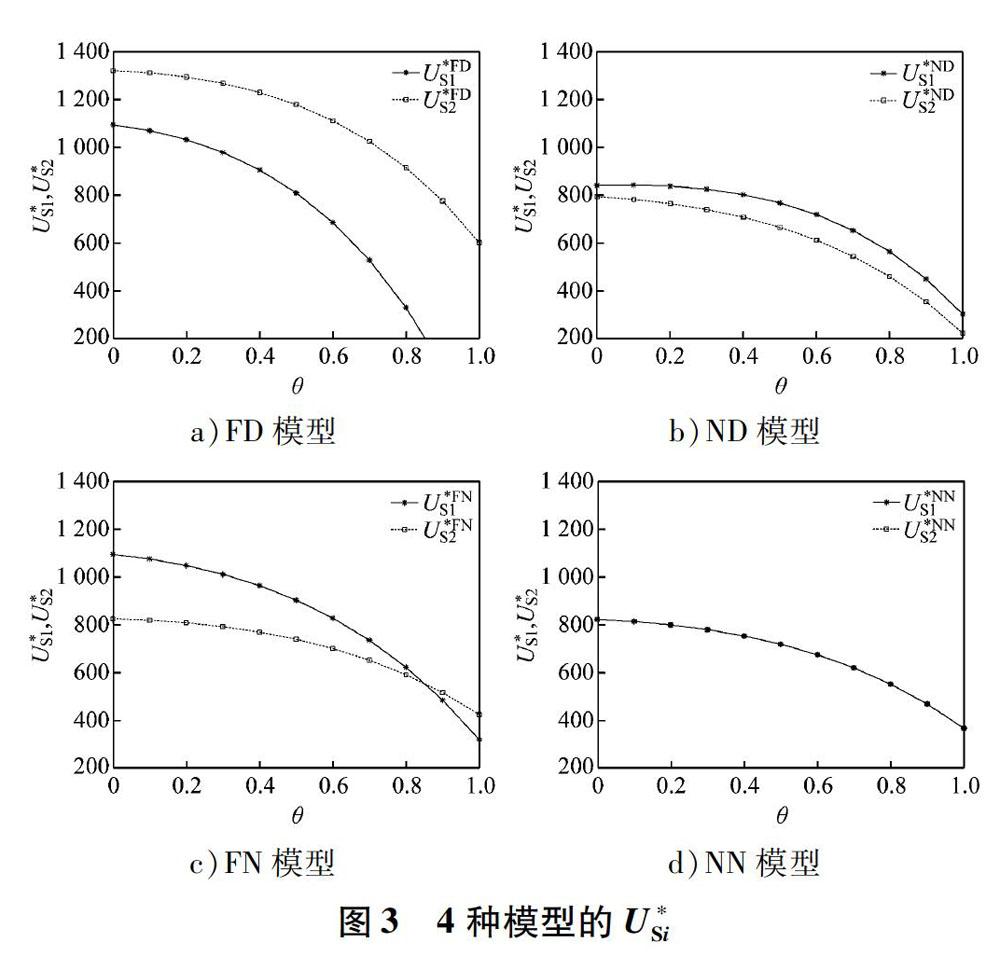
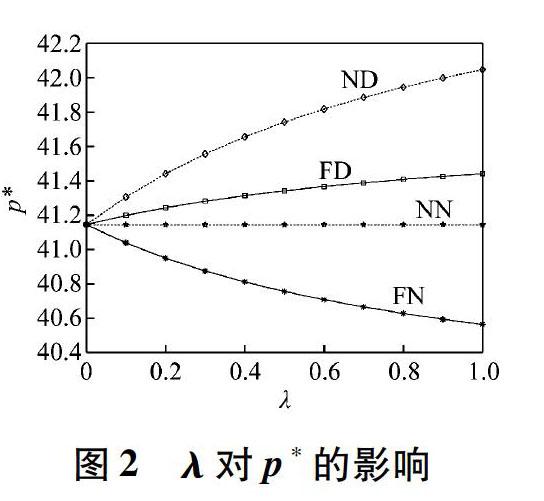
命题1 港口企业的最优零售价随分配（对等）公平关切系数的增大而降低（提高）。不同模型的最优零售价满足p*FN

命题2 港口企业的最优效用随分配（对等）公平关切系数的增大而降低（提高）。不同模型的最优效用满足U*FNP

命题1和2说明港口企业的最优零售价和最优效用在ND模型中最高，在FN模型中最低。换言之，新参与的港口业务服务商的对等公平关切对港口企业的定价和效用有积极的影响，而当前的港口业务服务商的分配公平关切对港口企业的定价和效用有消极的影响。通过进一步计算可以得出，当η-1=θ时，p*FD=p*NN，U*FDP=U*NNP，该结果取决于η与θ之间的关系。在订单分配过程中，垂直利润率触发分配公平关切，水平利润率触发对等公平关切，当p-w=（η-1）w时，η增大，港口企业与港口业务服务商之间的单位利润差距就增大。因此，η越大，当前港口业务服务商的分配公平关切就越强。η-1=r′表示港口企业的净利润率，创新支持水平对订单量的影响随θ的增大而增大，因此港口业务服务商之间的利润差距随θ的增大而增大，这将影响对等公平关切的强度。定义ρ=r′/θ作为两种公平关切的相对强度，可以得到命题3。

如果ρ>1，则净利润率大于横向竞争系数，由分配公平关切引起的负面效应更加显著，从而FD模型中港口企业的最优零售价和最优效用都比NN模型的低;如果ρ<1，则出现相反的结果，并且对等公平关切更强，最终对港口企业的最优零售价和最优效用产生积极的影响;如果ρ=1，则对等公平关切的积极影响恰好抵消分配公平关切的消极影响，使得两个模型中港口企业的最优零售价和最优效用相等。

命题1、2、3可解释如下：如果当前港口业务服务商不关注纵向订单分配公平性，新参与的港口业务服务商侧重横向比较，那么港口企业可以设定最高零售价并且获得最大效用;如果当前港口业务服务商有强大的讨价还价能力且新参与的港口业务服务商缺乏竞争动力，那么这对港口企业来说最不利。在实际情况中，港口企业可以通过调整价格系数与横向竞争系数的关系来优化港口业务服务商的选择。

1.4.2 港口业务服务商的最优创新支持水平

从港口业务服务商的角度出发，分析4个模型最优创新支持水平之间的关系，可以得到命题4。

命题4 e*1≤e*2在4个模型中都成立，不同模型中最优创新支持水平满足e*FNi

从命题4可以得出：新参与的港口业務服务商总是投入更高的创新支持水平，并且港口业务服务商的创新支持水平随对等公平关切系数增大而增大，随分配公平关切系数增大而减小，体现了港口企业引入具有强烈对等公平关切的港口业务服务商作为新参与者的重要性，可以刺激整个港口业务服务商的积极性。

2 港口企业的协调机制

基于以上分析可知，港口企业作为港口供应链的领导者，期望当前港口业务服务商有较少的分配公平关切，新参与的港口业务服务商具有较多的对等公平关切。为提高港口企业的最优定价、港口企业的效用和港口业务服务商的最优创新支持水平，本文提出一个协调机制，即港口业务服务商向港口企业支付成员费μ获得成员资格，港口企业设定利润分享率β与每个港口业务服务商分享利润。4种模型具有协调机制的效用函数如下：

通过以上结果，可以得到命题5。

命题5-1 在协调机制下，当β<θ/（η-1）时，U·*NDP>U·*FDP，U·*NDP>U·*FNP，U·*NDP>U·*NNP。也就是说，在ND模型中港口企业的效用总是最优的。

命题5-1表明：当利润分享率β小于某一阈值时，港口企业效用仍能在ND模型中达到最大。究其原因，除了分配公平关切和对等公平关切的影响，利润协调机制会促进港口业务服务商和港口企业共同创造价值，从而得到更多的利润。当β>θ/（η-1）时，利润协调机制作用强烈，对等公平关切作用相对较弱，这时U·*NDP

通过比较有协调机制和无协调机制的结果，可以得出结论：随着协调机制的出现，港口企业的最优定价和港口业务服务商的最优创新支持水平都在提高。对于港口企业来说，FD模型参数需要满足式（24），才能确保在4个模型中其效用可以得到提高，即U·*P-U*P>0。由于ND模型、FN模型和NN模型都是FD模型的特例，所以在上述参数条件下都满足U·*P-U*P>0。

命题5-2说明：通过协调机制可以缩小港口企业与港口业务服务商之间的利润差距，从而减少分配公平关切带来的负面影响，提高港口企业自身的效用。随着港口企业之间的竞争加剧，港口企业已经不再局限于提升自身能力，利润协调机制逐渐成为港口供应链发展的新趋势。

通过命题5-1和5-2可以得出结论：港口企业作为订单分配的领导者，可以引入本文提出的协调机制。通过这种方式，港口企业可以获得最优定价和最大效用，港口业务服务商可以获得最优创新支持水平。

3 数值模拟分析

使用MATLAB R2018a进行数值模拟分析，以进一步探讨公平关切和协调机制的影响。设置α=60，η=1.2，k=4，θ=0.3，c1=c2=0.01，β=0.06，λ=0.6。

3.1 公平关切系数λ对p*的影响

通过图2可以看出：在ND模型中港口企业的最优定价随公平关切系数的增大而提高;在FN模型中，港口企业的最优定价随公平关切系数的增大而降低;在FD模型中，决策受两种公平关切影响。基于4种模型的最优价格满足p*FN

3.2 公平关切系数λ对U*Si的影响

由于U*Si的理论解的复杂性，使用数值模拟来说明两种公平关切的影响。图3表明，随着θ的增大，港口业务服务商的效用减小，说明港口业务服务商之间的竞争对其效用有负面影响。进一步分析发现，在当前参数设置下，分配公平关切会增大港口业务服务商的效用（图3c和3d），对等公平关切会减小港口业务服务商的效用（图3b和3d）。

下：与对港口企业效用的单调递增（递减）影响不同，这两种公平关切对U*Si的影响是双重的。具体来说，对于对等公平关切，一方面，它将促进命题4中所描述的创新支持水平的提高，然后促进最终订单数量的增加，这对港口业务服务商的效用有正面的影响;另一方面，创新支持水平的提高也会带来更高的创新成本，从而导致效用的减小。对于分配公平关切，两方面的影响正好相反：分配公平关切导致创新支持水平下降，进而对效用产生负面影响;节约的创新成本又会增大效用。因此，在图3a中，随着θ的增大，港口业务服务商2的优势在于创新支持水平带来的利润大于创新成本，从而在当前参数设置下获得更大的效用。

3.3 协调机制的影响

从图4可以看出，在当前的参数设置下，协调机制对港口企业在4个模型中的最优效用有积极的影响（α=60，η=1.2，k=4，θ∈[0，0.6]，c1=c2=0.01，β=0.06，λ=0.6，μ=30），命题5得到了证明。上界（U·*P）与下界（U*P）之间的差异随着θ的增大而减小，这意味着协调机制的有效性减弱。这是因为当港口企业的效用随港口业务服务商之间的激烈竞争而增大时，港口企业需要与港口业务服务商分享更多的利润，因此效用的增长速度下降。

4 结束语

本文构造了由一个港口企业、一个当前的港口业务服务商和一个新参与的港口业务服务商组成的港口供应链。运用博弈论方法，比较了两个港口业务服务商表现出4种公平关切组合的不同模型，探讨了分配公平关切和对等公平关切对订单分配的影响，并且创新性地在港口供应链的订单分配模型中加入两种不同类型的公平关切。特别是该模型的决策序列是不同的，研究结果可以为港口企业在订单分配过程中对港口业务服务商的选择提供依据。结果表明：港口企业的最优定价和最优效用随新参与的港口业务服务商的对等公平关切的增强而提高，随当前港口业务服务商的分配公平关切的增强而降低。当两类公平关切共存时，如果公平关切的边际收益相等，那么港口企业的最终决策取决于横向竞争系数θ与价格系数η之间的关系。否则，最终的决策将进一步受公平关切系数的影响。当仅存在对等公平关切时，港口企业可以达到最大效用。此外，本文還提出一个协调机制来优化订单分配过程中的决策，提高港口企业的效用，实现港口供应链的决策优化。通过数值分析发现，本文提出的协调机制可以使港口企业效用最大化，从而可以有效地削弱分配公平关切的负面影响。在合理的参数设置下，不管两类公平关切系数之间的关系如何，4种模型的决策都可以得到优化，港口企业可以利用此协调机制实现效用的提高。

另外，本文为港口供应链订单分配的决策者提供了一些有意义的见解。首先，港口业务服务商由于进入市场的顺序不同，会表现出不同类型的公平关切。当仅存在新参与的港口业务服务商的对等公平关切时，港口企业可以获得最大效用;当仅存在当前港口业务服务商的分配公平关切时，港口企业只能获得最小效用。因此，港口企业可以更有策略地选择合适的港口业务服务商。在实践中，现有企业与新进入企业的共存情景和竞争关系非常普遍，因此本文的研究成果可以在许多行业推广应用。

本文的研究模型仍然存在一定的局限性。首先，本文构建了一个特殊的研究背景，在这个背景下，当前的港口业务服务商表现出分配公平关切，而新参与的港口业务服务商表现出对等公平关切。其次，本文重点研究的是一次博弈，而不是重复博弈。当前的港口业务服务商不清楚新竞争者的存在，因此忽略了当前的港口业务服务商可能改变其决定的情况。最后，本文主要讨论了以港口企业为领导者的订单分配优化，主要对港口企业的效用进行了讨论;港口业务服务商作为跟随者，其创新支持水平的提高可以帮助其获得更多的订单，因此本文只对港口业务服务商的最优创新支持水平进行了分析，没有展开对港口业务服务商效用的讨论。

参考文献：

[1]VALLS J F C. Models and algorithms for berth allocation problems in port terminals[D]. València： University of València， 2017.

[2]CHEN Yefen， SU Xuanming， ZHAO Xiaobo. Modeling bounded rationality in capacity allocation games with the quantal response equilibrium[J]. Management Science， 2012， 58（10）： 1952-1962. DOI： 10.1287/mnsc.1120.1531.

[3]陆永明. 港口供应链利益共享契约的协调机制[J]. 上海海事大学学报， 2017， 38（1）： 52-56. DOI： 10.13340/j.jsmu.2017.01.011.

[4]严南南， 丁伯根. 收益共享契约下港口供应链协调的双层规划模型[J]. 上海海事大学学报， 2019， 40（3）： 80-86. DOI： 10.13340/j.jsmu.2019.03.014.

[5]高洁， 真虹， 李建丽. 港口与供应链的互动发展[J]. 上海海事大学学报， 2009， 30（3）： 40-45.

[6]杨波峰. 公平关切下基于政府补贴的港口供应链协调机制研究[J]. 物流技术， 2016， 35（9）： 120-124， 159. DOI： 10.3969/j.issn.1005-152X.2016.09.025.