一种对地姿态重定向的机动轨迹规划及控制方法

雷拥军 陆栋宁 关 新

1.北京控制工程研究所，北京100094 2.空间智能控制技术重点实验室，北京100094

对地遥感卫星姿态快速重定向可高效获取非星下点目标的遥感数据，以满足单轨大范围多目标成像、区域目标成像、立体成像及动态监视等需求[1-2]。通过星体姿态重定向将当前指向姿态快速过渡到目标指向姿态的快速机动问题在理论上为时间最优姿态机动控制问题，即考虑动力学、控制及角速度等约束下，从任意初始姿态到指定姿态的最小时间机动问题，已有大量文献开展最优轨迹求解方法的分析研究[3-8]。基于极大值原理必要条件求解的间接法难以获得解析最优解，因此相关文献借助于参数化方式将连续系统最优问题转化为一类非线性规划问题，进而采用直接法以寻求最优轨迹[9]。伪谱法在姿态重定向时间最优问题的直接求解中得到广泛应用[4-5,10]，其中基于勒让德伪谱法的姿态重定向时间最优轨迹求解方法在TRACE空间望远镜上得到验证。

考虑卫星动力学及环境等不确定性因素的影响，求解获得的机动优化轨迹一般作为跟踪控制的期望姿态指令输入。实际姿态重定向包括姿态快速调整与为适应载荷工作的姿态稳定两阶段，如典型遥感卫星Pleiades-HR[11]可在25s内实现60°姿态重定向且满足成像所需角速度幅值小于50μrad·s-1的要求。由于基于时间最优机动问题优化求解的方法一般存在难以满足在轨实时性要求、优化轨迹解析式难以获取而使得用于改善机动控制性能的前馈控制无法实现、以及时间最优控制为多次饱和控制切换方式等问题，制约了其在姿态快速重定向中的应用。文献[5]基于贝塞尔伪谱法对航天器姿态机动最优轨迹求解方法进行了研究，并利用Matlab软件中的IDVD优化求解器在2.33G主频处理器及1Gb RAM的台式计算机上开展解算验证，对10s量级时长的姿态机动轨迹求解，尽管所需机时由小时量级大幅降低至数秒量级，但在主频100MIPs量级以下及内存容量受限的星载计算机[12-13]上达到实时性要求仍具有一定差距。

鉴于可采用简洁解析式描述机动运动规律，并可克服前述时间最优化方法求解所存在的相关问题，绕欧拉轴旋转方式在姿态快速重定向研究中获得广泛应用[14-19]。当限定绕欧拉轴旋转时，时间最优问题可转化为欧拉角的单变量规划问题，根据最优控制理论得到的Bang-Bang形式为最优轨迹，即机动过程中控制力矩在正负饱和量间切换一次，不少文献[14-19]采用了该轨迹规划方式。文献[3,5-7]等研究表明，通常情况下绕欧拉轴旋转不是时间最优的，其中文献[5]通过90°姿态重定向对比仿真表明，其相比由伪谱直接法在足够多节点设置下求解得到最短时间指标增加约3%，但当节点数设置不足时会出现大于绕欧拉轴旋转的情况。进一步考虑结构挠性振动问题，文献[20-21]基于绕欧拉轴转动方式分别提出的正弦、混合正弦等形式的欧拉角平滑轨迹规划方法，有效减弱了挠性振动激发且减缓机动力矩输出对执行机构机电部件的冲击，文献[22-23]研究了Bang-Bang及正弦形式的轨迹参数优化方法。

对于对地遥感卫星，除实现传统意义下姿态重定向使得载荷指向地面观测目标外，还需根据目标点成像要求对姿态动态调整，如通过偏航姿态调整[24]以克服地球自旋运动引起的TDI-CCD相机像移问题[25]，及SAR卫星需偏航和俯仰二维导引[26]以实现全零多普勒导引等，因此在实际任务中，星体姿态机动开始及终点相对轨道坐标系还具有期望的相对运动。传统姿态重定向为固定边界时间优化问题(即机动开始与终端点航天器姿态相对轨道参考系无相对运动)，然而，严格来说，在具有相对速度边界条件时的姿态重定向是无法通过绕固定欧拉轴旋转的方式来实现的[5]。

针对综合考虑轨道运动、观测目标指向调整及对目标瞄准时姿态动态调整的复杂姿态重定向问题，本文基于绕欧拉轴旋转轨迹规划策略及反馈与前馈相结合的控制策略，提出了一种边界条件具有相对运动的姿态机动轨迹规划及跟踪控制方法，并结合数学仿真对方法的有效性进行了验证。

1 姿态跟踪控制器设计

以卫星本体坐标系相对惯性坐标系的四元数q和角速度ω来描述的卫星姿态运动学方程为

(1)

式中，qv与q4分别为q的矢量部分与标量部分。

刚体卫星姿态动力学方程为

(2)

式中，J为星体转动惯量；u为施加于星体的力矩。

为了实现对非星下点的地面目标观测，工程上往往将姿态重定向问题转化为姿态跟踪问题。设定跟踪目标坐标系相对于惯性坐标系的四元数为qr及角速度为ωr(期望姿态机动轨迹具有一定光滑性)，并满足关系式

(3)

式中，qrv与qr4分别为qr的矢量部分与标量部分。

(4)

式中，qev与qe4分别为qe的矢量部分与标量部分。

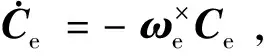
(5)

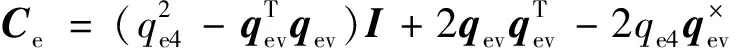
为提高机动动态性能，在控制过程中往往对动力学方程中的确定项进行前馈补偿。针对式(5)，在星体转动惯量确知情况下的补偿量为

(6)

当姿态跟踪误差为小量时，Ce可近似为单位阵，于是式(6)可近似为

(7)

对式(4)和(5)组成的系统，结合式(6)或(7)给出的补偿量，可采用如下具有补偿的PD控制器实现星体三轴姿态跟踪控制

u=kpqev+kdωe+ucmp

(8)

式中，控制参数kp和kd均为正定矩阵。

当式(8)实现精确补偿时，在其控制作用下可使得闭环系统具有全局渐近稳定特性[24]，即有qev→0，ωe→0。为实现精确补偿控制，除了需星体转动惯量参数确知外，由式(6)可知还需获取期望角速度ωr及其时间导数的信息。

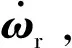
2 姿态重定向运动规划

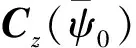
经姿态机动时间Δt=t-t0后，当前轨道系Ot相对姿态机动初始t0时刻轨道系O0的方向余弦阵COtO0为

式中，ωo为轨道角速率。

CBtOt=CB0O0

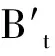
式中，qv=esin(χ/2)；q4=cos(χ/2)。

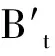
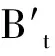
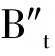
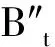
3 姿态规划轨迹参数解算

以t0时刻B0系作为惯性系，所规划的姿态机动在t时刻星体相对以t0时刻B0系为惯性系的期望姿态方向余弦阵为

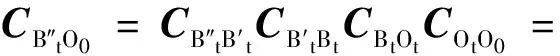
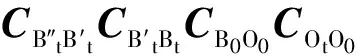
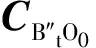
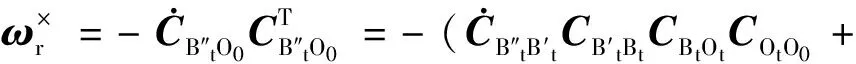
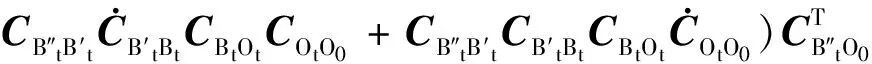
(9)

由方向余弦阵时间导数关系，式(9)可整理为

(10)

即有

(11)

对式(11)所示ωr求时间导数，有

(12)

利用式(10)，式(12)也可表示为

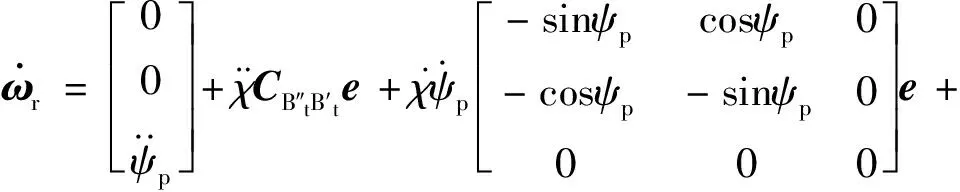
(13)

式中，

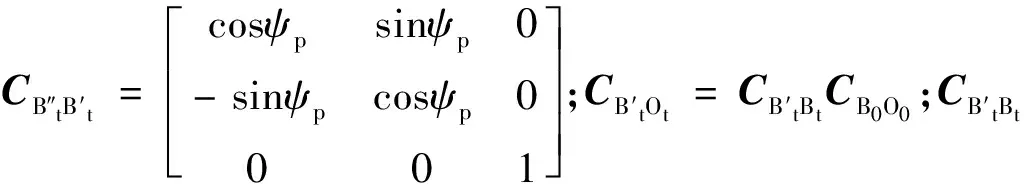
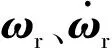
(14)

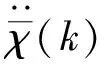
4 数学仿真校验

本节针对所给出的姿态重定向轨迹规划策略及控制算法进行仿真验证。卫星运行于轨道高度为500km的太阳同步轨道，对应轨道角速率为ωo=0.00101(rad·s-1)，卫星转动惯量及PD控制器参数如下[15]

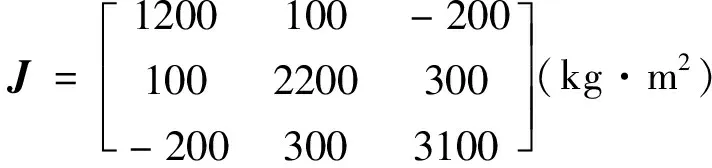
kp=diag{60, 110, 155}

kd=diag{379.2, 695.2, 979.6}

星体初始为对地姿态且偏航角以设定规律ψr=5sin(60ωot+π/6)(°)运动。在50s时姿态开始机动，对地目标姿态滚动角与俯仰角分别为45°与35°。机动最大角加速度及角速度容许最大幅值分别为0.2(°)/s2与2.5(°)/s，按机动加速度正弦形式[20,23]进行机动姿态轨迹规划。

4.1 具有前馈补偿的反馈控制仿真

采用式(8)所示具有补偿的PD控制器，具体补偿量计算方式见式(7)，控制周期Ts选取为0.125s。

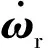
图1 具有PD补偿控制的欧拉姿态角

图2 PD补偿控制的欧拉角速度

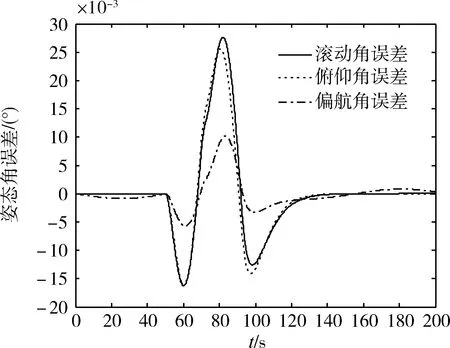
图3 PD补偿控制的欧拉角误差

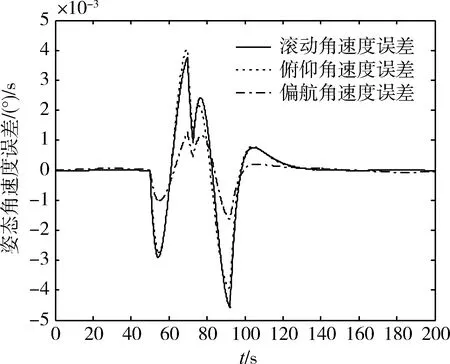
图4 PD补偿控制的欧拉角速度误差

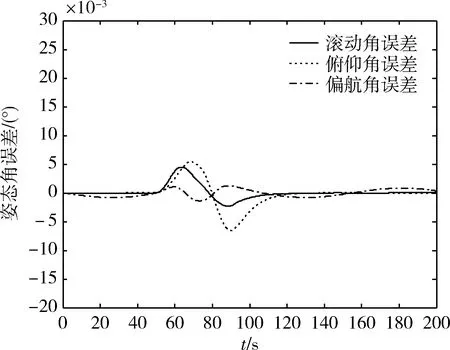
图5 加速度修正PD补偿控制的欧拉角误差

图6 加速度修正PD补偿控制的欧拉角速度误差

4.2 仅有前馈力矩补偿的开环控制仿真

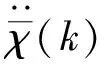
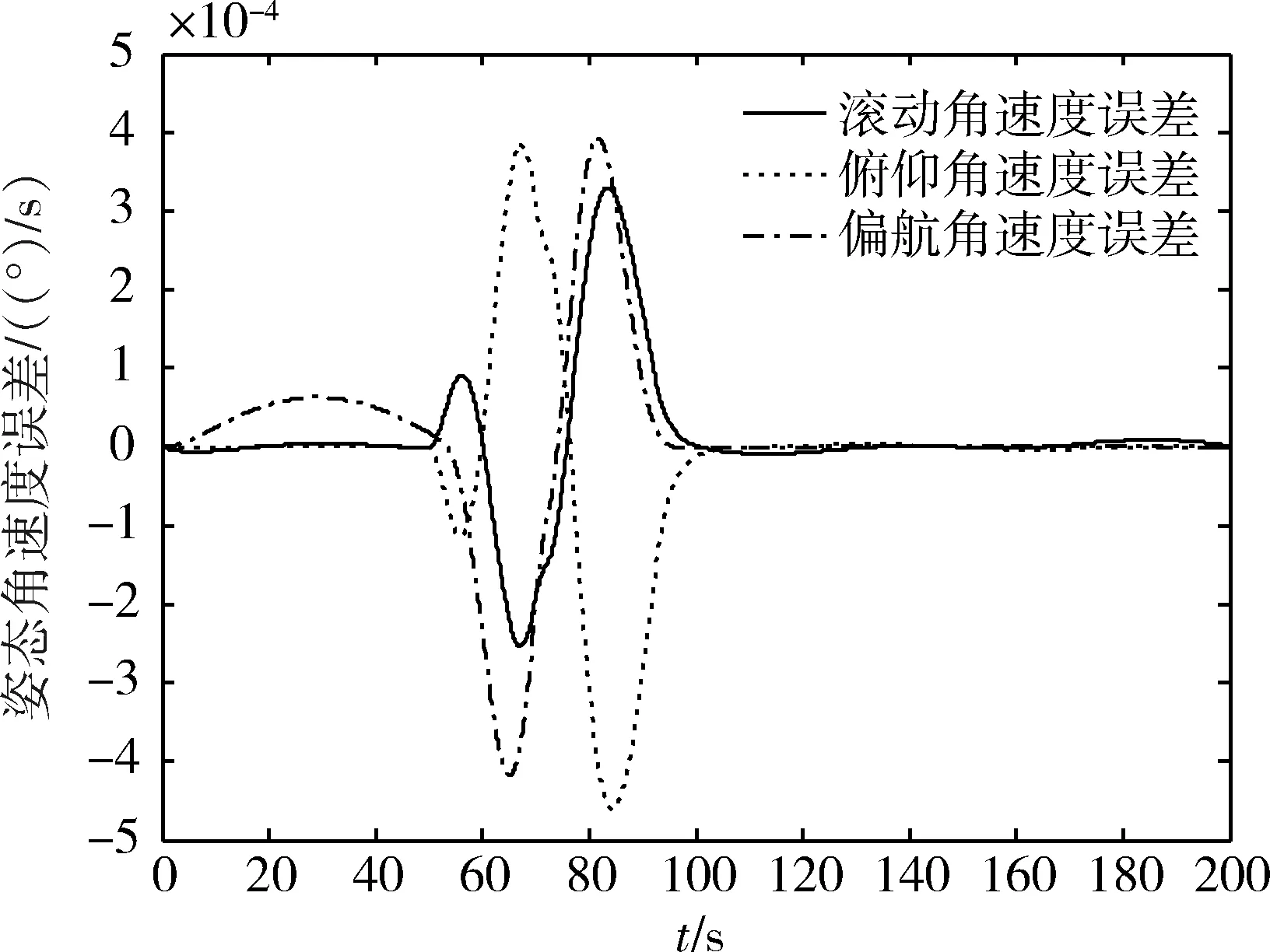
图7 开环控制欧拉角速度误差(Ts=0.125s)

图8 开环控制欧拉角速度误差(Ts=0.0625s)

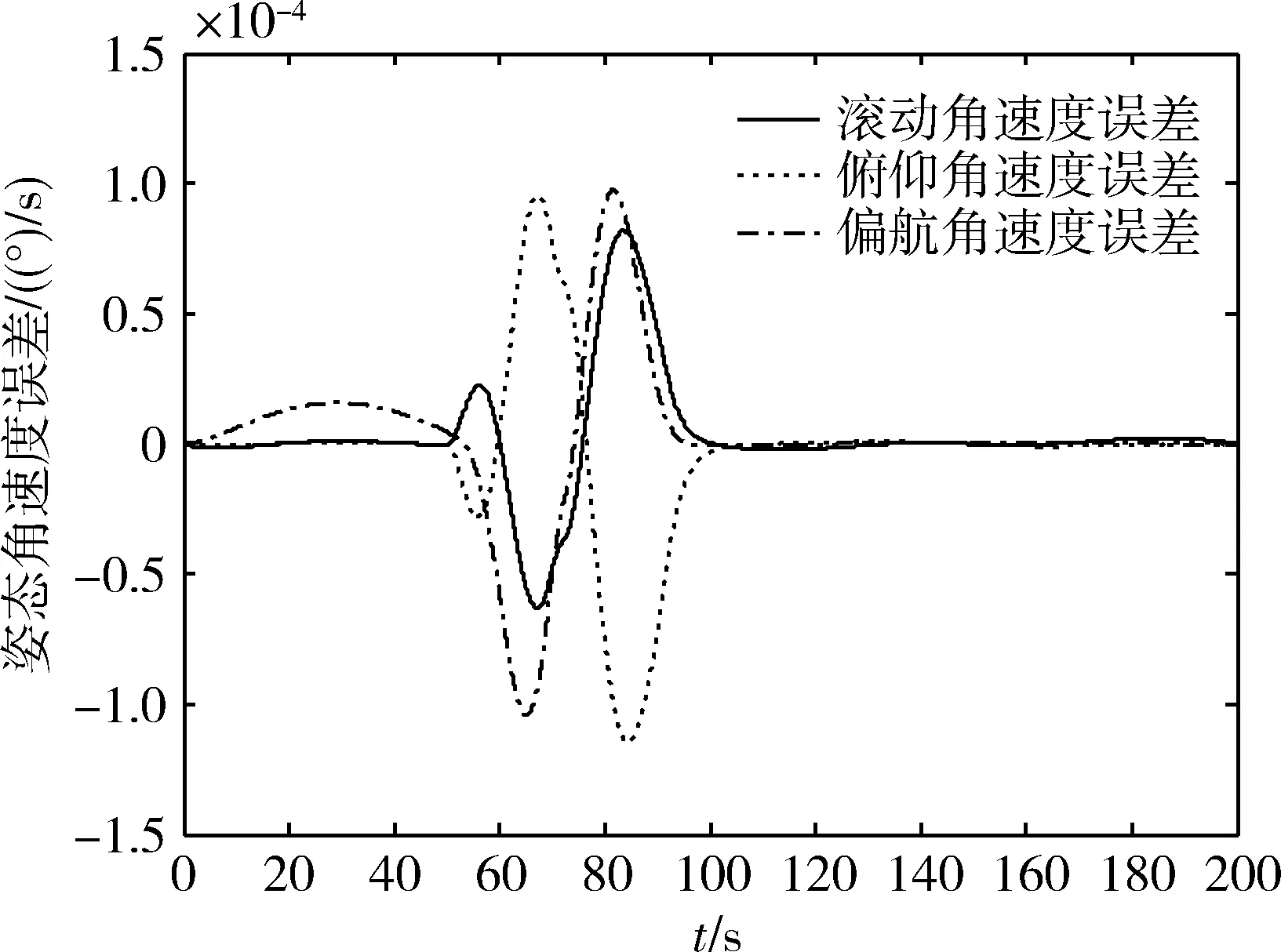
图9 开环控制欧拉角速度误差(Ts=0.03125s)

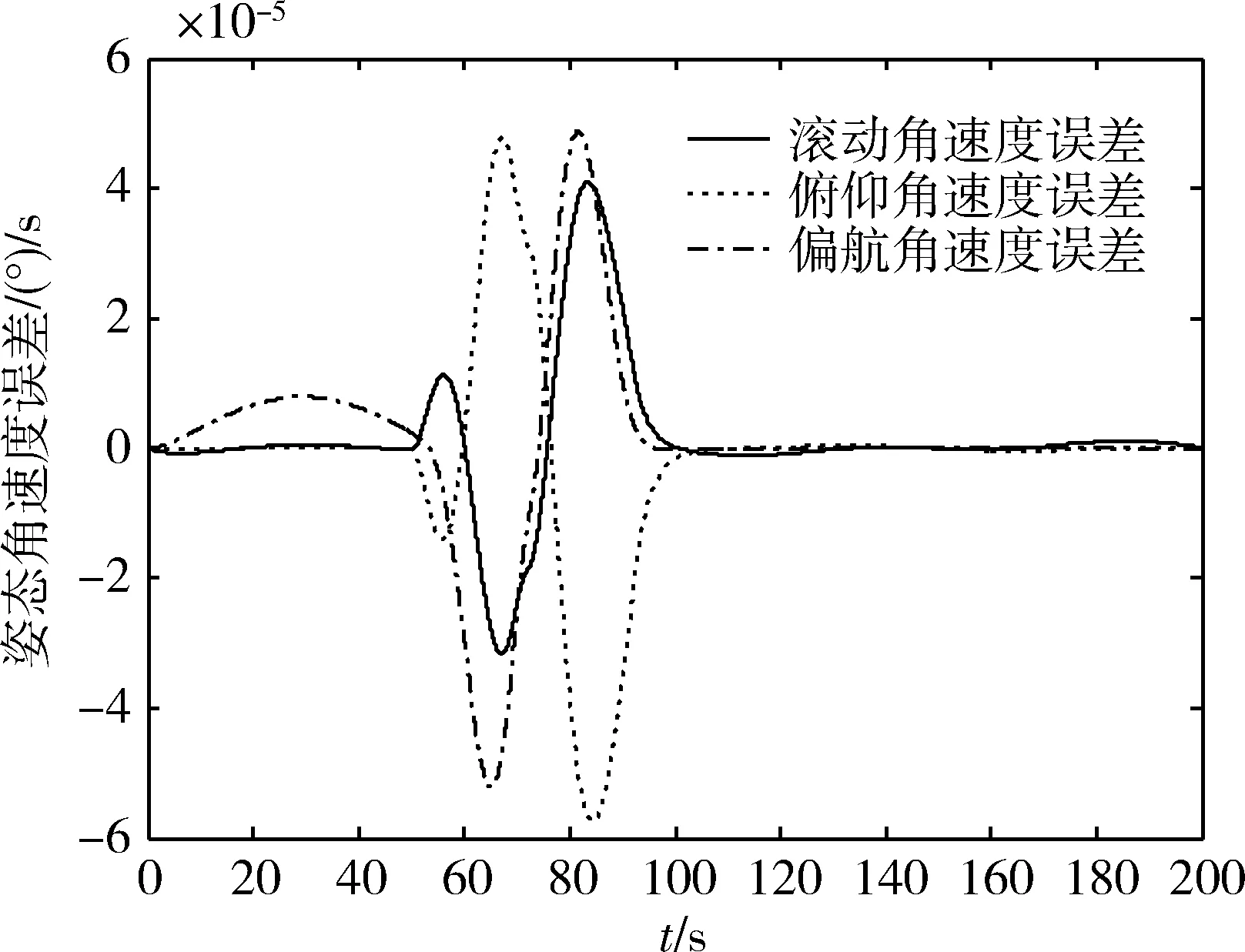
图10 开环控制欧拉角速度误差(Ts=0.015625s)

5 结论

针对具有指向实时调整需求的对地遥感卫星姿态快速重定向问题，基于绕欧拉轴旋转轨迹规划及反馈与前馈相结合控制策略，提出了一种边界条件具有相对运动的姿态机动轨迹规划及跟踪控制方法。规划得到的解析表达式形式简单，可为高性能姿态跟踪控制提供精确的力矩前馈补偿输入。

根据不同控制周期的开环仿真结果比较得知，前馈补偿控制下姿态误差随采样周期减小而线性减小，从而表明在对象参数确知的情况下，基于文中给出的前馈补偿方法可实现力矩精准补偿，其误差仅由系统离散实现引起。对于系统离散化产生的补偿误差，采用冲量等效原理对补偿量进行修正。对比仿真表明，修正后的补偿控制可将姿态误差降低半个数量级以上。