微型同位素辐射能收集器二维悬臂梁机电建模

杨 柳,彭建设,孙付春,曹文继，李晓晓，孙丰云

(成都大学 机械工程学院, 成都 610106)

0 引 言

数十年来，微机电系统(Micro-Electro-Mechanical-Systems, MEMS)在航空航天、通信、医疗、生物、汽车等领域发挥着巨大作用[1-5]。由于微型设备的尺寸达到了亚μm级，其能量供应成为了制约微器件和微系统发展的重要因素。为了解决微能源供给问题，各国学者展开了广泛的研究，目前微能源解决方案大致可分为微型化学电池[6]、微型环境能量收集器[7]和微型同位素辐射能量收集器[8-10]。微型化学电池易受环境温度和燃料浓度及流量的影响，在某些恶劣环境中无法正常使用。微型环境能量收集器极大地受限于环境因素，可靠性较低[11]。微型同位素辐射能量收集器是一种以同位素辐射能为能量源的收集装置。由于同位素材料具有衰变周期长、释放能量密度大、释放能量稳定性高和不易受外界环境影响的特点，因此可为微能源提供高能量密度、长寿命、稳定的能量源[12]。Li等[13]首次制备出一种“放射能-机械能”循环的直接转换型同位素辐射能量收集器，并利用一维机电模型对其进行性能分析。然而，一维模型过于简化，导致其无法完整描述微型同位素辐射能量收集器的各项性能。

本文基于欧拉-伯努利梁理论，提出一种更切合实际的二维微悬臂梁机电模型。基于Li等的实验装置和数据，本文模型的准确性得到了充分验证。同时，利用新模型解决了一维模型无法解释的问题。

1 装置原理及等效电路

“放射能-机械能”循环的直接转换型同位素辐射能量收集器原理如图1所示[13]，微悬臂梁收集由63Ni放射的β粒子。由于电荷守恒，放射源上会留下等量相反的电荷。因此，微悬臂梁与放射性同位素薄膜之间会形成一个静电力，此静电力会使微悬臂梁向同位素薄膜方向运动。一段时间之后，微悬臂梁最终会与薄膜相接触，通过电荷转移而发生电荷中和。电荷发生中和的同时，微悬臂梁与薄膜之间的静电力消失，微悬臂梁自身的弹性回复力会使其回到初始位置，并开始下一个周期。微悬臂梁在自主往返运动过程中相当于一个电荷积分器，将核能储存然后转换成机械能与电能。图1同时给出了整个装置的等效电路，由电流源、电阻器和可变电容器3部分构成。电流源用来等效由放射性同位素薄膜发射出的电荷，电阻器用来等效漏电路径，可变电容器用来等效微悬臂梁与同位素薄膜。

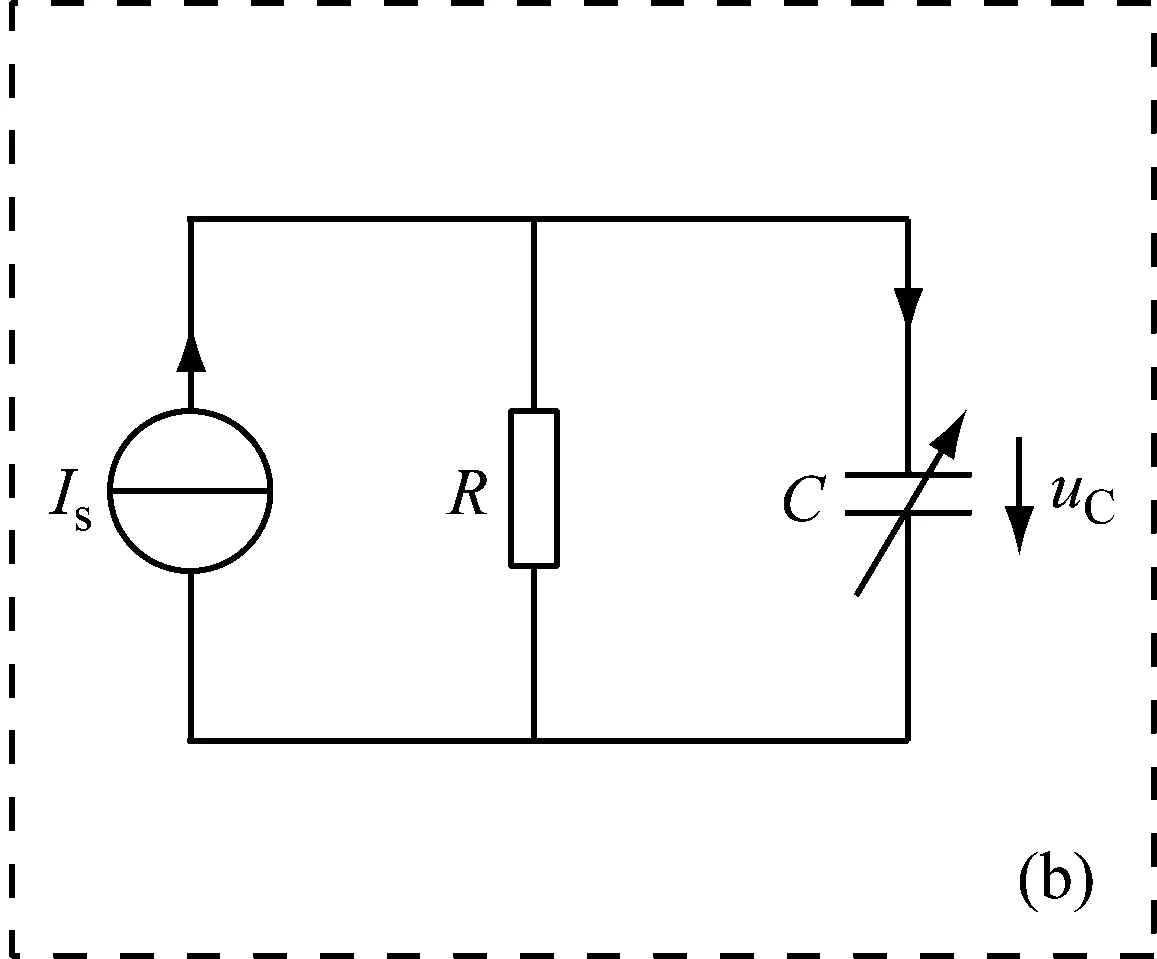
图1 放射性同位素供能的自主往返式微悬臂梁系统的原理图和等效电路图

等效电路中的电流源取决于同位素薄膜的放射性活度N，63Ni放射的是β粒子，则其等效电流为：

I= 1.6×10-19×N

(1)

式中：N为放射性活度，Bq；I为等效电流，A。

等效电路中的电阻器用来描述所有可能的漏电路径，如：β粒子使气体分子电离(Ions)；β粒子撞击微悬臂梁发射出次级电子(Secondary electrons)等。

等效电路中的空气隙电容器由微悬臂梁电极和放射性同位素薄膜电极构成，其电容会随着电极距离的改变而改变。

2 二维微悬臂梁机电模型

根据基尔霍夫第一定律，有：

(2)

式中：u为微悬臂梁和薄膜源之间的电压；R为漏电阻；ε0为真空介电常数；A为电容器的有效面积；t为时间；g为微悬臂梁和薄膜源之间的距离；a为收集系数(a<1)，用来表示发射的总电流中被微悬臂梁收集的部分。

在大气压下，收集的电荷很容易被电离和极化的空气分子中和，导致式(2)中的R很小，从而导致微悬臂梁与薄膜之间的漏电流很大，这已经被实验现象所证实。为了获得一个大的R值，装置必须在真空条件下工作。当压力减小到0.4～67 mPa时，R达到1015～1014Ω的量级。因此，式(2)可以简化为：

(3)

由于微悬臂梁与放射源之间的间隙和渐近角都很小，可假设构成平行板电容器，电容器的电容C和能量Wc分别为：

(4)

根据电势能和虚位移原理，综合考虑式(3)、(4)，微悬臂梁与放射源薄膜垂直运动方向的静电力为[14]：

(5)

根据实验现象，微悬臂梁从初始位置下拉到与放射源薄膜相接触的过程可合理假设为一个准静态过程。基于欧拉-伯努利梁理论，微悬臂梁的控制方程为：

(6)

同时，微悬臂梁的边界条件为：

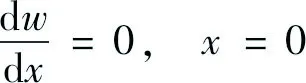
(7)

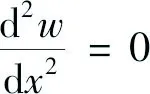
(8)

式中:E为微悬臂梁弹性模量；I0为微悬臂梁横截面惯性矩；w为挠度；L为微悬臂梁长度；F(x,t)为微悬臂梁单位长度所受的静电力，其表达式为：

(9)

式中:LS为放射源薄膜的长度；l0为坐标原点到放射源的距离；H(x-l0)为亥维赛函数(Heaveside function)，其定义为：

(10)

因此，微悬臂梁的控制方程可重写为：

(11)

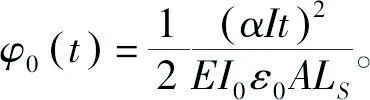
根据式(7)、(8)和(11)，可得到微悬臂梁的剪力方程、弯矩方程、转角方程和挠度方程分别为：

(12)

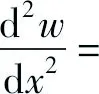
(13)

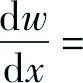
(14)

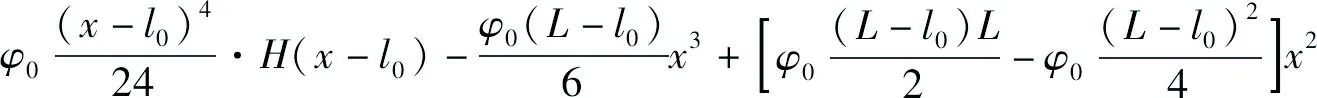
(15)

由式(15)可得微悬臂梁自由端挠度为：

w(L,t)=

(16)

当自由端挠度从0开始增大到g0时，微悬臂梁与放射源薄膜相接触放电，意味着一个往返周期结束，所用时间为：

(17)

式中，g0为微悬臂梁和放射源薄膜之间的初始距离。因此，影响往返周期的因素有微悬臂梁的几何尺寸、微悬臂梁的抗弯刚度、微悬臂梁的收集效率、放射源的放射强度、放射源的相对位置、微悬臂梁和放射源薄膜之间的初始距离等。

模型中微悬臂梁能把63Ni薄膜发射出的核能转换成机械能和电能存储于其中。由于微悬臂梁的下拉过程可近似认为是准静态过程，因此微悬臂梁中存储的机械能可近似等于其应变能。根据弹性力学理论，应变能为：

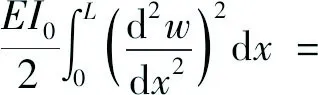
(18)

微悬臂梁中存储的电能为：

(19)

63Ni薄膜在一个周期内发射出的总能量为：

wall=N×Wa×T

(20)

式中：Wa=17.4 keV为63Ni放射电子的平均能量；T为一个往返周期。由于在周期末尾，微悬臂梁与放射性薄膜接触，梁上的电能为零，因此，最终输出的能量形式为微悬臂梁的最大机械能WS,max。在一个周期内，装置能量转换效率为：

η=WS,max/Wall

(21)

3 结果与讨论

为了验证二维机电模型的有效性和准确性以及相对于一维模型的优势，下面将进行各种算例结果的比较。注：本文中所采用的实验装置数据参考文献[15]：微悬臂梁长L=4 cm，微悬臂梁宽b=3 mm，微悬臂梁厚h=90 μm，初始间隙g0=118 μm，微悬臂梁弹性模量E=108 GPa，收集系数α=29%，放射性活度N=3.59×107Bq，放射源薄膜长度LS=1 cm，真空介电常数ε0=8.854×10-12F/m。

图2绘出了梁自由端与放射源之间的距离随时间变化的曲线，其中实心点为实验数据，虚线为一维模型理论计算结果，实线为本文模型理论计算结果。可以看出，两种模型解都能较好地解释实验结果，实验数据中下拉周期为161 s，一维模型的下拉周期为163 s，而本文模型的下拉周期为160 s。需注意，为与实验结果更接近，一维模型中的初始间距与实际情况并未完全相符，而本文模型中的初始间距选取与实际情况完全一致。由以上数据结果可以看出，相对于一维模型，本文模型能更好的解释实验结果。

图2 微悬臂梁自由端与放射源之间的距离随时间变化曲线

图3给出了不同初始间隙条件下微悬臂梁的往返周期变化曲线，其中实心方点为实验数据，虚线为一维模型理论计算结果，实线为本文模型理论计算结果。同样可以看出，两种模型都能较好地解释实验结果，相比之下，本文解与实验结果更一致，进一步体现出了本文模型的优势。

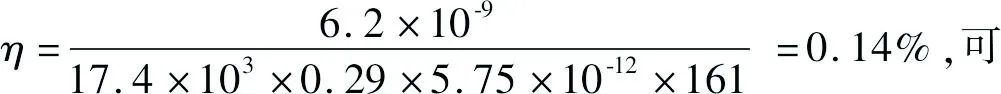
图3 不同初始间隙条件下微悬臂梁的往返周期

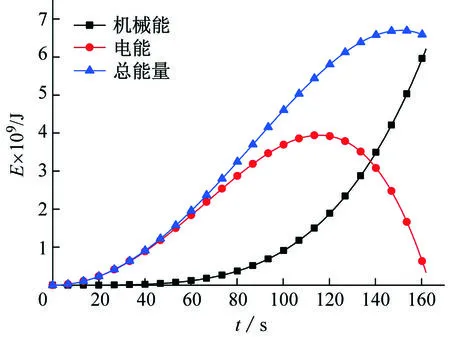
图4 能量随时间变化的曲线

图5～7分别给出了微悬臂梁上不同位置的等效剪力Q/φ0、弯矩M/φ0和转角θ/φ0分布图。可以看出，微悬臂梁上剪力呈线性分布，从固定端到3 cm处剪力保持恒定且最大，随后剪力线性减小，在悬臂端时剪力减为0；微悬臂梁上固定端处弯矩最大，随后线性减小，3 cm之后呈非线性状态减小直至最终在悬臂端处降为0；微悬臂梁上转角呈非线性分布，从固定端处的0开始增至悬臂端处的最大值。需要指出的是，剪力、弯矩和转角分布关系无法从一维模型中得到，这是因为一维模型把梁简化成弹簧-质量块，丢失了许多力学参数。而本文的二维模型能避免此问题，使模型计算结果与实验结果更吻合。

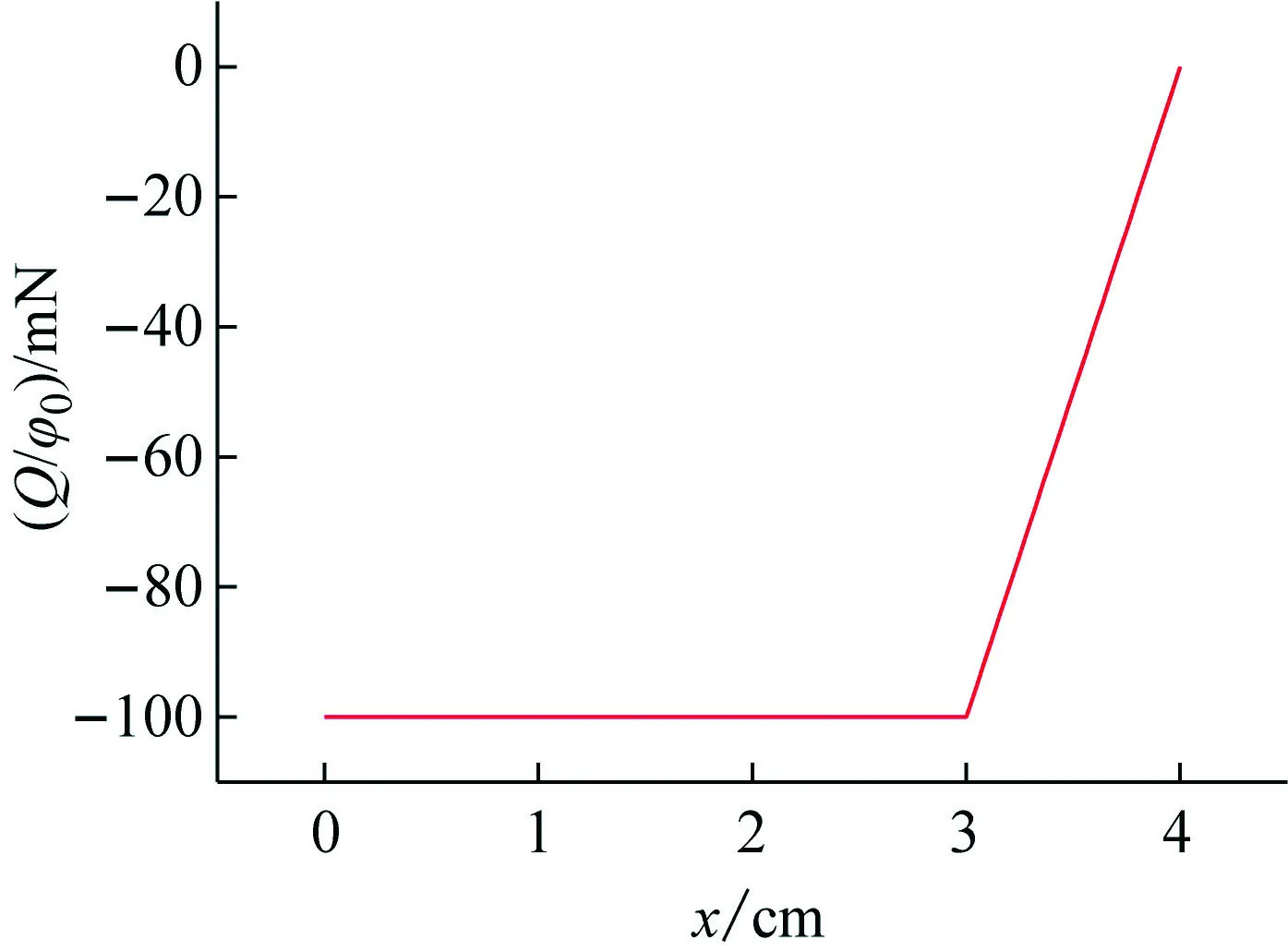
图5 微悬臂梁上不同位置剪力分布图

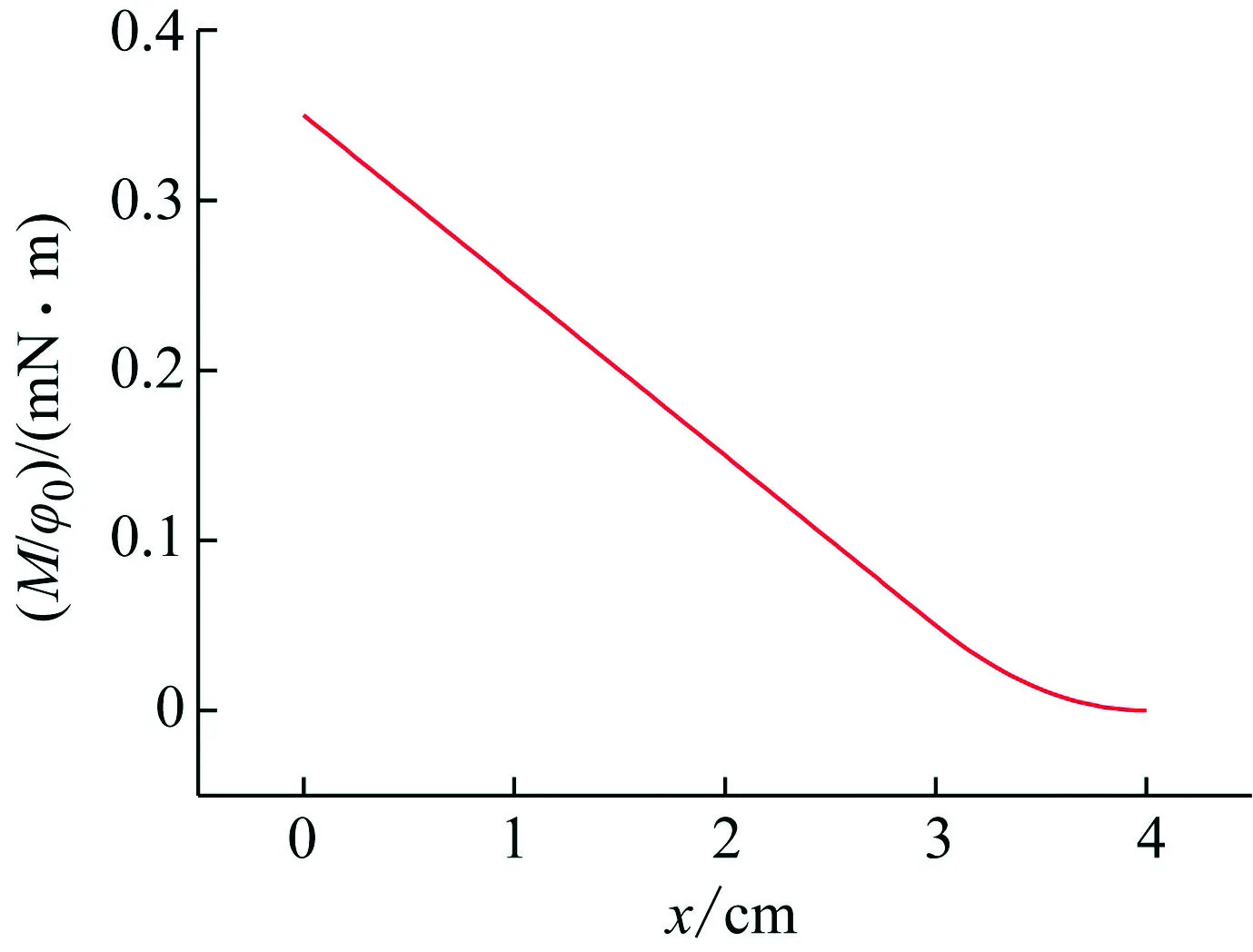
图6 微悬臂梁上不同位置弯矩分布图

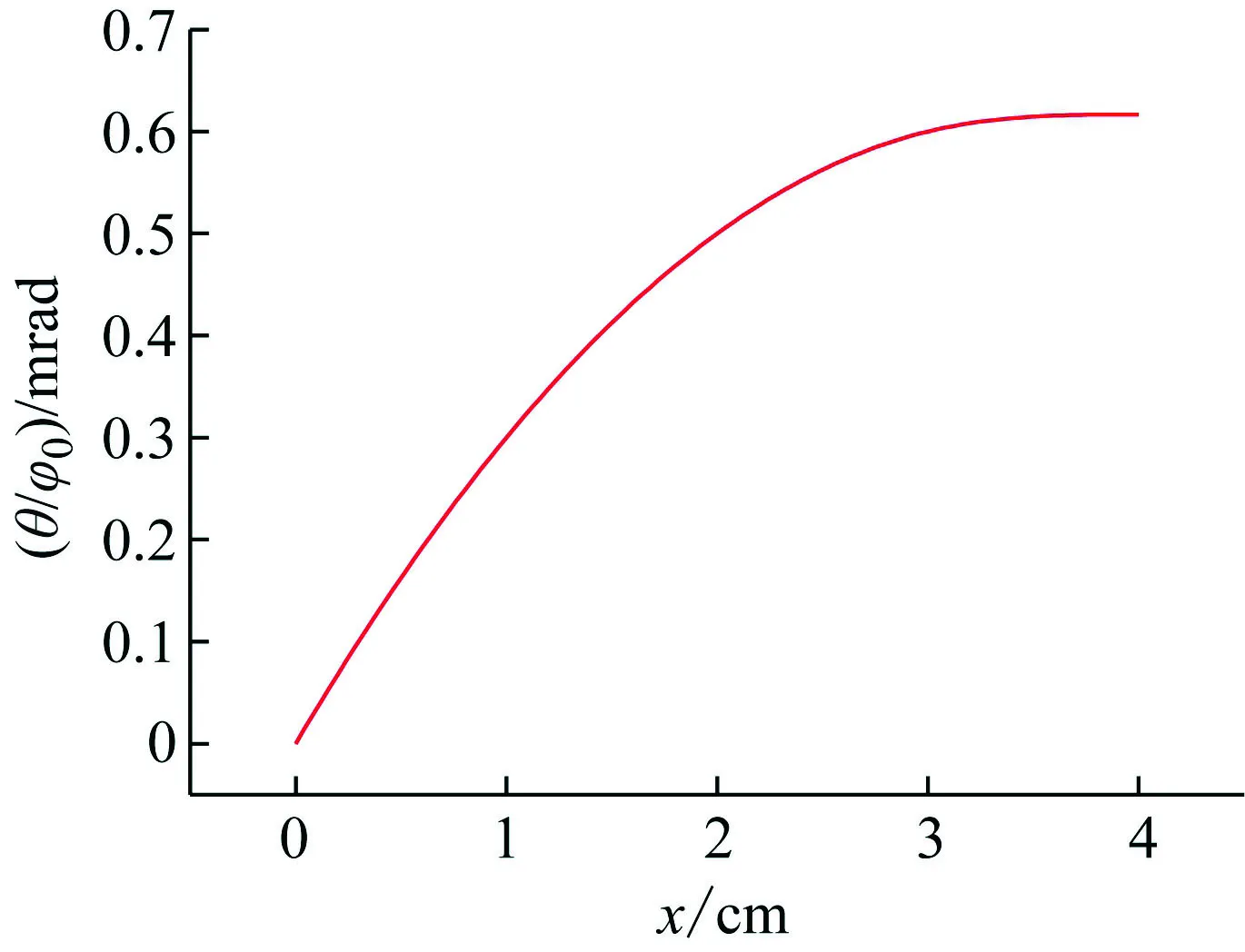
图7 微悬臂梁上不同位置转角分布图

4 结 语

研究结果表明：相对于一维模型，二维机电模型能更有效地分析微型同位素辐射能收集器各项性能；影响下拉时间的因素包括：微悬臂梁的几何尺寸、抗弯刚度、收集效率和放射源的放射强度、微悬臂梁和放射源薄膜之间的初始距离。