利用相空间重构短时间间隔的吸收太阳能预测方法
2020-04-28汪心怡姚彦鑫董未名
汪心怡,姚彦鑫,董未名
(1.北京信息科技大学 光电测试技术及仪器教育部重点实验室;高端装备智能感知与控制北京市国际科技合作基地,北京 100010; 2.中国科学院自动化研究所,北京 100080)
0 引 言
据统计,无线通信占整个信息和通信技术产业能源消耗的15%~20%。利用新型再生能源,如热、振动、太阳能、声学、风,甚至周围的无线电能量来驱动无线网络的研究兴趣极大地提高,最终在无线网络领域形成了可吸收能量(Energy Harvesting,EH)的概念[1]。其中太阳能吸收能量以其获取方便,可以预测等优势,得到广泛应用[2]。以前工作大多集中于讨论光伏发电系统输出功率的短期预测,预测方法大致可分为物理法和统计法。物理法模型构建复杂、参数选取复杂、运算量比较大,适合大规模发电站使用;统计法主要依据数学统计理论,模型建立简单、计算量小,预测精度高,不过需要大量的历史数据,如自回归滑动平均、马尔科夫链预测、支持向量机预测、人工神经网络(Artificial Neural Network,ANN)预测模型[3]等。其中ANN以其高精度获得广泛应用,网络的形式可以有很多变化,如递归神经网络[4]、小波网络等。
考虑光伏发电系统输出功率受到外界气象因素的影响呈现出一定的混沌特性[5],可以引入相空间重构对数据进行处理[6]。文献[7]中对样本空间进行重构,确定最佳的延迟时间和嵌入维数,使新的样本能够表征原始时间序列动态特性,在此基础上运用BP进行短期预测。实验结果表明,短期预测精度得到提高。文献[8]中结合相空间重构理论与动态递归神经网络提高了预测精度。文献[9]中基于相空间重构小波神经网络进行水电站发电量预测,并借助具有全局搜索能力的改进粒子群优化算法对小波神经网络特征参数进行优化,提高模型的精度和泛化能力。
将相空间重构与递归小波神经网络结合的研究还没有,而且研究对象也没有针对较短时间间隔的太阳能吸收能量。本文将针对此问题开展研究。
1 预测模型
1.1 相空间重构
混沌是指在确定系统中出现的具有一种貌似无规则的、类似随机的现象,混沌不是简单的无序,而是没有明显的周期和对称。混沌吸引子是时间序列相空间的子空间,它使得相轨迹有一定的规律可寻,从而保证了混沌系统的可预测性。Lyapunov指数是对时间序列混沌性进行确定检验的一种非常重要的方法,可以运用小数据量法计算得到,正的Lyapunov指数意味着混沌现象。
重构相空间的两种方法:导数重构法和坐标延迟重构法。坐标延迟重构法中可以采用C-C法[10]联合计算相空间重构嵌入维数和时间延迟。C-C法具有容易操作、计算量小、抗噪性强、对小数据组可靠等特点。考虑混沌时间序列{x(n)|n=1,2,…,N},假设重构嵌入维数为m,时间延迟为τ,对其进行相空间重构后得到
X={Xi|i=1,2,…,N-(m-1)τ}
其中,Xi为重构相空间中的相点[11],
Xi=[x(i),x(i+τ),,x(i+(m-1)τ)]
1.2 递归小波神经网络
递归神经网络在逼近非平稳信号时能更好适应信号的动态特性,神经网络结合小波变换能够充分利用小波的局部化性质和神经网络的自学习能力,将递归小波网络和小波结合组成的网络将具有较强的逼近和容错能力、较快的收敛速度和较好的预测效果[12]。
在小波神经网络中,隐含层神经元选择不同的小波激励函数对小波网络的收敛会有不同的影响,同时对算法的复杂性有明显的影响。根据光伏发电功率数据序列的特点,小波基函数选用Morlet小波作为隐层神经元的激励函数。Morlet母小波是余弦调制的高斯波,其时域和频域的分辨率高,广泛用于预测领域[13],其函数如图1所示,表达式为
φ(x)=e-x2/2cos 1.75x

图1 Morlet母小波函数图
在Elman型递归神经网络的基础上,将小波函数作为隐含层的激励函数构成递归小波神经网络[14],如图2所示。隐含层神经元的作用函数为小波基函数。承接层神经元的输入是隐含层神经元的输出,承接层和输入层的输出同时输入到隐含层。承接层神经元也是一种记忆单元,储存了隐含层神经元上一步的输出,使得网络具有较好的动态性能。

图2 递归小波神经网络结构模型
1.3 相空间重构与递归小波网络结合预测模型
本文考虑对光伏发电功率数据时间序列进行相空间重构预处理,可提高预测精度和减少预测对天气的依赖性,较为适合短时间间隔的太阳能能量吸收的预测。重构后使用的数据及神经网络模型相对简单,可以轻量级运行于通信节点。对光伏发电功率时间序列进行混沌特性分析,并对其进行相空间重构。然后将重构后数据输入神经网络进行预测。
重构光伏发电功率时间序列{x(t),t=1,2,…,1 099}的相空间,假设其嵌入维数为m、时间延迟为τ,得到重构相空间中相点表示为
X(i)=[x(i),x(i+τ),…,
x(i+(m-1)τ)]
(1)
式中:i=1,2,…,N,N=1 099-(m-1)τ为光伏发电功率重构相空间中的相点个数。因此,得到一个N×m的重构相空间数据矩阵为:
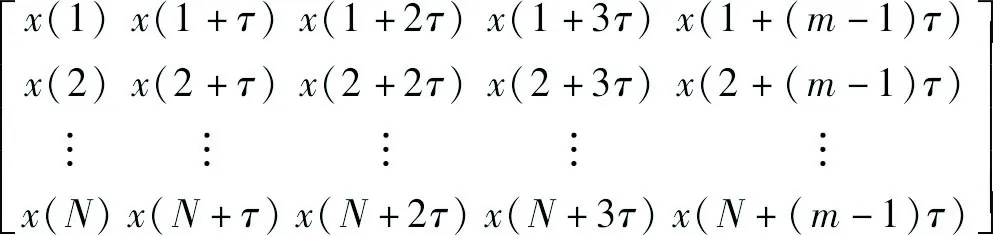
(2)
则递归小波神经网络输入层节点个数确定为m,输出层节点个数为1。
网络训练集的输入为
X(j)=[x(j),x(j+τ),…,x(j+(m-1)τ)]
则对应的网络输出为
Y(j)=x(j+1+(m-1)τ)
其中,j=1,2,…,N-1表示网络输入输出训练数据对的标号。
经过对光伏发电功率进行小波分析,确定隐含层和承接层神经元个数。Hi(t)为第i个隐藏层节点的输出信号;hi(t)为隐含层神经元i的输入信号;φ(·)为小波基函数;ai(t)为小波函数伸缩因子;bi(t)为小波函数平移因子;θi是输入到隐藏层节点的常数偏置;α是从承接层输入到隐藏层的折扣值;W1、W2、v分别为输入层到隐藏层,隐藏层到输出层、承接层到隐藏层的权值矩阵。其中元素的下标,分别表示对应的关联节点。定义:
(3)
Hi(t)可表示为
此神经网络的动态方程可表示为:

(4)
设神经网络训练时间步从1~N,则一个训练周期后的总误差为
(5)
学习算法的最终目的是通过调节神经元之间的连接权值,使得总误差值逐渐变小,直至满足预先设定的条件。具体的方法是采用动态梯度下降算法。
神经网络的输入、输出为1 d的光伏发电功率数据,如果数据之间数量级差别比较大,神经网络的预测误差会很大,并且在训练过程中神经元容易饱和。因此,在训练神经网络之前需要对数据进行归一化到[0,1]之间。
由于相空间重构是预先进行操作,实际预测时输入数据量少,而且递归小波神经网络本身的强动态适应性和激励函数的正则性将使得的预测方法的预测误差小,收敛速度快,可实施性强。
2 预测模型分析与评价
2.1 数据处理与相空间重构
吸收太阳能能量的预测时间间隔考虑应用特点,一般预测间隔较短,远小于光伏电站0.5 d、若干小时的预测间隔。更短,秒、毫秒量级的时间数据在公开资料较为难于获取,需要实验得到。采用Solar Radiation Monitoring Laboratory, University of Oregon网站上公布的Portland地区的2015年7月份的太阳能发电数据。数据中包括太阳辐射强度、环境温度、平均风速、风向、光伏发电功率等。太阳能板倾斜角度为30°,方向朝南。数据选取时段为6:00~19:00,采样间隔为5 min,则每种数据1 d的数据量大小为157。
数据7月1~7日光伏发电功率数据构成时间序列{x(t),t=1,2,…,n},序列长度为n=1 099。根据C-C算法,确定此序列相空间重构的最佳延迟时间为τ=4、嵌入维数m=5。用选取的嵌入维数和时间延迟对序列进行相空间重构,根据小数据量法得到最大Lyapunov指数为λ=0.020 9。由于λ>0,所以序列具有混沌特性。
选取2015年7月1~8日、7月14日、7月15日共10 d的光伏发电功率数据构成时间序列,采样时段为6:00~19:00。分别计算嵌入维维数、时间延迟、最大Lyapunov指数等,计算结果如表1所示。

表1 不同采样间隔的时间序列相空间重构参数对比
2.2 神经网络预测及比较分析
实验场景1递归小波神经网络处理非相空间重构数据。由于每天的数据为6:00~19:00时间段采集间隔5 min得到的157个数据,递归小波神经网络的输入层、输出节点个数为157。隐含层和承接层神经元的个数经过计算和试凑得到M=18。根据确定的网络结构参数建立递归小波神经网络。
首先将选取的数据归一化处理,然后将7月1日~7月7日的数据训练预测模型,训练用前1 d的光伏发电功率预测后1 d的。训练完成后,用7月7日预测7月8日的光伏发电功率。建立同样结构的Elman神经网络,训练设置的参数与递归小波神经网络相同。

图3 训练误差对比
表2 不同方法的预测情况对比

网络名称训练次数训练误差预测总体相对误差递归小波神经网络5220.00098550.0495Elman神经网络7480.00098900.0575

图4 预测值与实际值各点相对误差曲线图
由图4可知,6:00~8:00和17:00~19:00这个两个时间段单点相对误差比较大,在其他时间段单点相对误差比较小。结果比较理想。
以上直接对太阳能数据采用神经网络的缺点在于,网络的输入层和输出层节点个数是按照输入、输出的数据量来选择的。如果预测间隔较短,输入的数据量很大,则会导致网络结构变得非常复杂,并且使得训练网络过程中的计算量很大,不利于实际的应用。
实验场景2重构与未重构数据对不同天气情况适应度对比。对于全年随机挑选的40 d数据,按照太阳能辐射情况、天气观测值等,将天气分为晴天,阴/雨/多云转晴两种情况,预测模型分别采用未重构数据构建的Elman预测模型,输入为相空间重构数据的m输入1输出Elman预测模型1,输入为相空间重构数据的m-1输入1输出Elman预测模型2,进行多次实验后平均预测结果如表3所示。
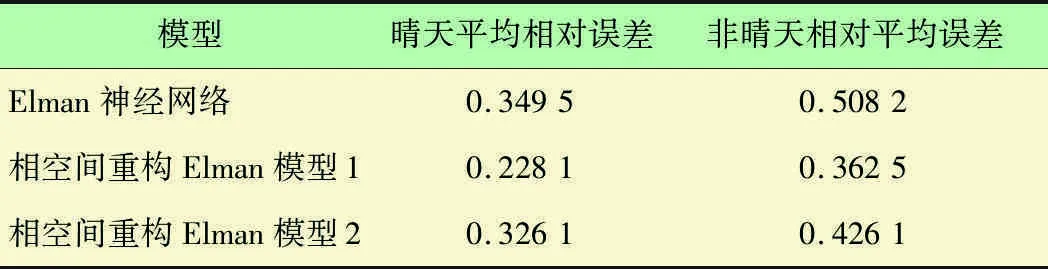
表3 模型预测结果比较
可见,仅选取太阳能吸收能量作为输入预测时,预测精度相对采用重构数据的模型低,而且在天气变化时预测误差增加较大。因此直接用太阳能数据作神经网络的输入,很多文献都采取了先用灰色分类、SVM、SOM网络将数据按照不同天气类型先进行聚类,再依据不同天气类型分别用神经网络进行预测的方案。
如表3所示,与未重构时的Elman神经网络预测模型相比,重构后的m输入1模型与m-1输入1输出模型均能在非晴天实现可接受精度的预测,m输入1输出神经网络模型预测性能最好。可见本文模型应用混沌理论进行预测,对实时天气数据和相关因素的敏感度低很多,可在不对天气情况分析的条件下用于对吸收能量进行短时预测。
实验场景3递归小波神经网络处理相空间重构数据,不同时间间隔的处理结果。
用7月1~7日的光伏发电功率构建神经网络训练数据集,对7月8日光伏发电功率进行预测。分别用采样间隔为10、20、30 min的光伏发电功率数据训练神经网络,对7月8日的光伏发电功率进行提前10、20、30 min预测。表4为了不同采样间隔光伏发电功率预测情况。

表4 不同采样间隔光伏发电功率预测情况
采用第2.3节介绍的训练算法对7月8日的光伏发电功率进行提前5 min预测,总体相对误差为0.028 3。误差小于5%的数据占76.43%以上,且大部分都在8:00~18:00时间段,相空间重构和递归小波神经网络结合方法能够较准确地完成预测。
2.3 计算量分析
由于相空间重构的计算可以预先计算,本节分别衡量相空间与递归小波网络结合的计算量和非相空间重构的数据与BP网络结合预测的在线计算量。神经网络计算主要集中于非线性激励函数和乘法计算的计算量。根据文献[15]可知,通过处理,非线激励函数计算量大约相当于8次乘法的计算量。假设相空间与递归小波网络的输入、隐层、输出层节点个数分别为P、Y、Q。非相空间重构的数据与BP网络结合的输入、隐层、输出层节点个数分别为P′、Y′、Q′。
神经网络非线性激励函数核算:普通神经网络和递归网络,非线性激励操作的计算量为O(Y+Q)。进行相重构后,输入、隐层、输出层节点个数大大降低,不过迭代次数增加,为P′次。
乘法核算:普通神经网络,乘法计算次数对于一次迭代为O((P′+Q′)Y′)。对于递归网络一次迭代是O((P+Y+Q)Y),需要迭代Y次。那么折算为乘法计算量后,对比相空间重构与递归小波网络结合的计算量O(Y+Q)·P′×8+O((P+Y+Q)Y)·P′和O(Y+Q)×8+O((P+Y+Q)Y)。
表5为折算为乘法的等效计算量比较。

表5 相空间和Elman结合计算量与BP算法等效为乘法的计算量比较
当预测间隔为5 min,非相空间重构计算量大概是相空间重构计算量基本一致。但是,注意,当预测时间间隔进一步变短时,比如2.5、1.25 min,相空间与Elman结合方法的计算量比BP算法的计算量小。时间间隔越短,本文提出的方法的计算量较小的效果越明显。当预测间隔为1.25 min时,计算量降低25%以上。相空间与Elman结合预测模型相对简单,预测精度高,而且不需要存储大量的历史数据和未来预测数据,相对普通BP或者未进行相空间重构数据进行预测是轻量级的。
这里没有对小于5 min的数据做预测实验的原因是网站上的测量数据时间间隔最小为5 min。不过实验已经说明了本文方法具有预测精度高、轻量级运行的优越性。
综合仿真结果可知,虽然相空间重构后只用了少数天数的数据,但是预测精度较高,且对天气变化的敏感度相对较低。这是由于相空间重构本身表现了混沌序列本身的内在结构特征,包含了不同天气因素复杂非线性影响的关系。使用相空间重构与递归小波网络结合的方法后,预测精度更是得到了极大的提高,时间间隔较短时,预测计算量相对较低。本文提出的基于相空间重构和递归小波神经网络结合预测具有可行性,在预测间隔变短时候,能够以较低的代价更准确的预测未来光伏发电系统的输出功率。
3 结 语
本文研究了适用于与太阳能吸收节点的轻量级、短时间间隔的吸收太阳能能量预测方法。建立了相空间重构与递归小波网络结合的光伏发电系统输出功率预测模型。验证了相空间重构表现了混沌序列本身的内在结构特征,包含了不同天气因素复杂非线性影响的关系,可以更高效表达数据特征。使用小波递归网络使系统的动态性提高,学习能力增强。因此新模型的收敛速度、预测精度等都得到了较大提高,而且预测计算量降低。本文提出的预测模型具有较好的天气、环境等的适应度,具有预测精度高,短时间间隔计算量低等优良性能。吸收太阳能能量的预测需要对天气相对不敏感,在短时间间隔可以轻量级运行在节点上的预测算法,因此本文的方法将有望在能量吸收节点的短时间间隔发电功率预测中获得广泛应用。进一步可以研究如何为降低短时间间隔情况下的预测计算量而改进模型。
