振动信号过完备字典完整训练样本重构性能研究

郭俊锋，杨 文

（兰州理工大学机电工程学院，甘肃 兰州 730050）

1 引言

滚动轴承作为机械设备中一种必不可少的通用零部件，其工作状态直接影响着机械设备的正常运行。滚动轴承振动信号蕴含着机械设备工作过程中的大量信息。传统的以奈奎斯特采样定理为基础的振动信号A/D检测与采样会产生巨量的监测数据，这些数据对后续存储、传输及处理形成了潜在的计算压力。

压缩感知理论[1]的出现为机械振动信号检测与采样提供了新的思路，可以远低于奈奎斯特采样率所要求的数据高概率重构信号。目前对压缩感知理论在机械振动信号的研究逐步深入，主要包括三个方面：振动信号的稀疏表示、测量矩阵和重构算法的设计[2]。信号的稀疏表示是实现压缩感知理论的前提和基础，选择适合机械振动信号的稀疏域并获得信号在稀疏域上的最稀疏表示就显得尤为重要。近几年，信号在过完被字典上的稀疏分解得到了广泛关注。一些研究尝试采用K-SVD算法[3]从样本集合中学习训练得到过完备字典后对信号进行稀疏表示，进而提高信号的压缩重构性能。K-SVD算法主要分三步实现：字典初始化、稀疏编码和字典更新。文献[4]针对K-SVD算法在字典更新过程中消耗时间较长的问题，从更新的字典原子列数出发对算法进行改进，并将其应用于齿轮箱振动信号，提高了算法的速率。文献[5]基于K-SVD过完备字典对振动信号进行稀疏表示，与离散余弦过完备字典相比，在保证压缩比的同时有更好的重构性能，提高了算法的精度。文献[4-5]分别从字典更新和稀疏编码入手对K-SVD算法的重构性能进行了分析研究，较传统K-SVD算法和DCT过完备字典，虽然改进算法和KSVD过完备字典在一定程度上性能有所改善，但均未考虑样本对字典学习算法、特征提取及故障识别方法的影响。

样本是信号内容详细信息的表达，而在实际应用中，用于训练过完备字典的样本集合中只包含一种信号类型，对重构信号的精确性和稳定性影响较大。为了进一步改进信号的重构性能和后续特征提取、故障识别的精度，采用多种形式的振动信号构造样本，解决样本集合中信号类型不足的问题，通过不同的样本得到不同的字典学习结果。采用在数据样本集合中随机选取K个原子构成初始字典的方式，研究K-SVD过完备字典完整训练样本对滚动轴承振动信号重构性能的影响。首先构造用于学习的样本集合，使其尽可能多地包含各种信号成分；然后从所构造的样本集合中随机选取K个原子作为初始字典，采用K-SVD算法对初始字典进行训练更新得到过完备字典，获得滚动轴承振动信号的最稀疏表示；最后利用高斯随机测量矩阵对振动信号进行压缩测量，基于压缩测量数据采用OMP算法对信号进行重构。并选用美国西储大学轴承数据进行实验验证。

2 压缩感知基本框架

压缩感知理论[6-8]是一种新的压缩与采样同时进行的信号采集理论，其采样过程，如图1所示。由图1可知：滚动轴承振动信号f∈Rn在变换域Ψ上是稀疏的或可压缩的，其线性投影的数学模型为：

图1 压缩感知理论框架Fig.1 The Theory Framework of Compression Sensing

式中：Φ∈Rm×n（m＜＜n）—测量矩阵；x—信号 f在变换基 Ψ 上的稀疏表示系数；y∈Rm×1—测量数据；||x||0—稀疏系数中非零项的个数。

为了方便求解，当信号本身或在某个变换域下具有稀疏性且测量矩阵满足约束等距性（RIP）[9]时，可采用l1范数代替l0范数求解优化问题。

目前上述优化问题的求解方法主要有凸松弛算法和贪婪算法。凸松弛法所需采样点数少，但计算复杂度较高，主要有基追踪（BP）算法[10]；贪婪算法计算复杂度较低，但需要的测量数据多且精度较低，主要有匹配追踪（MP）算法和正交匹配追踪（OMP）算法。综上所述，选用OMP算法[11]进行振动信号的重构。

3 基于过完备字典完整训练样本的滚动轴承振动信号压缩重构方法

3.1 基于K-SVD算法的滚动轴承振动信号过完备字典完整训练样本设计

K-SVD算法是一种稀疏编码和字典更新交替进行的贪婪算法，其思想是使每个原子的重构误差在字典更新阶段最小。根据K-SVD算法的实现步骤，采用从数据样本集合Y中随机选取K个原子作为初始字典的方式，从样本集合中包含的信号类型出发对算法进行改进，分别构造单一信号样本集合、综合信号样本集合及单一故障信号样本集合，通过构造不同的样本集合获得不同的初始字典，从而获得更适合于滚动轴承振动信号的字典。通过构造3种包含不同信号类型的样本集合，分析同一滚动轴承振动信号在不同K-SVD过完备字典上的稀疏性，并研究滚动轴承振动信号基于K-SVD过完备字典的重构性能和不同样本集合对信号重构性能的影响。

3.2 基于过完备字典完整训练样本的滚动轴承振动信号重构方法的实现步骤

（1）选取美国西储大学轴承数据库振动数据，构造不同的样本集合Y。（2）随机选取样本集合Y中的K个原子作为初始字典D，基于K-SVD算法和OMP算法获得最优的过完备字典。（3）在K-SVD过完备字典上对滚动轴承振动信号f进行稀疏表示f=Dx。（4）选用高斯随机矩阵作为观测矩阵Φ，对n维信号f进行投影得到m维压缩测量数据y。（5）根据压缩测量数据y采用OMP算法对信号进行重构，并基于重构信号分析信号重构性能。

4 实验与分析

这里的所有实验均在MATLABR2014a进行编程运行，操作系统为Windows7。选用美国西储大学轴承数据进行实验验证。该试验对象为深沟球轴承，轴承型号为6205-RSJEMSKF，信号采样频率为12KHz。该试验在轴承外圈、内圈、滚动体上分别布置了单点故障，故障直径分别为0.007、0.014、0.021英寸（1英寸=2.54cm）。

4.1 样本集合的构造及其稀疏性分析

4.1.1 单一轴承振动数据样本集合的构造

首先选用故障负载为0HP（1HP=746W）、故障直径为0.007英寸（即0.1778mm）的驱动端外圈故障模式振动数据OR007@6实现单信号样本集合的构造。由于该振动信号是周期信号，为了训练字典的需要，故将信号进行扩展，选取0-512000采样点作为单信号样本集合Y1，然后从样本集合Y1中选取K个原子作为初始字典D，并选取上述信号长度为512的外圈振动数据作为测试信号。

4.1.2 综合轴承振动数据样本集合的构造

针对上述单信号样本集合Y1存在的问题，考虑构造包含多种信号类型的综合样本集合Y2，其构造方式如下：综合轴承振动数据和类别，如表1所示。共包括正常、外圈、内圈、滚动体故障的10种故障数据类型中的29种信号（信号长度分别为25600），选取0-512000采样点作为综合信号样本集合Y2，然后在综合样本集合Y2中随机选取K个原子作为初始字典D。

表中：Normal—正常状态；OR、IR、B—外圈、内圈、滚动体故障，其后的数字表示故障程度，@后表示故障点所处方位；DE—驱动端数据；FE—风扇端数据；BA—基座数据。

4.1.3 单一故障轴承振动数据样本集合的构造

为了使上述长度为512的外圈振动测试信号基于过完备字典即有较好稀疏性又有较高的重构精度，尝试采用仅包含外圈故障的多种信号构造单一故障样本集合Y3，其构造方式如下：表2为外圈单一故障轴承振动数据，故障直径为0.007、0.014、0.021英寸的9种信号（信号长度为76800），选取0-512000采样点作为单一故障样本集合Y3。

表2 外圈故障数据名称与类别Tab.2 The Name and Category of Outer Ring Fault Data

4.1.4 基于不同样本集合的K-SVD过完备字典的滚动轴承振动信号稀疏性分析

首先基于上述3种样本集合的构造方式，构造不同的样本集合，然后确定K-SVD算法中的五大参数：初始字典原子个数K=600、原子长度n=512、样本集合Y的原子个数N=1000、迭代次数J=10、稀疏表示振动信号所需最多原子个数L=10，最后选取上述信号长度为512的外圈振动数据进行滚动轴承振动信号的稀疏性分析。其中，测试信号的时域波形，如图2所示。

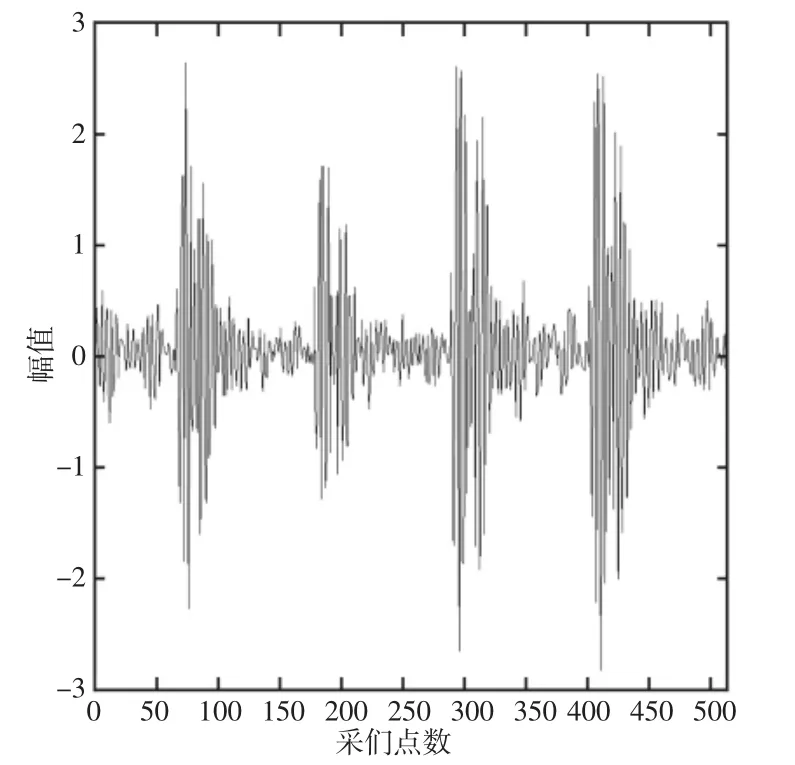
图2 外圈振动信号时域波形Fig.2 The Time Domain Waveform of Outer Ring Vibration Signal

将振动信号在不同K-SVD过完备字典上进行稀疏表示，采用OMP算法获得振动信号在过完备字典上的稀疏表示系数，迭代一定次数后对分解系数按绝对值降序排列后，如图3所示。

从图3可以看出经过多次迭代后振动信号在单一信号样本集合训练所得K-SVD过完备字典上稀疏表示系数呈指数衰减，且在迭代106次时衰减为0。而在综合信号和单一故障信号样本集合训练所得K-SVD过完备字典上的稀疏性相对较差，但其稀疏表示系数按绝对值降序排列后也呈指数衰减。说明振动信号在K-SVD训练所得过完备字典上稀疏性较好。

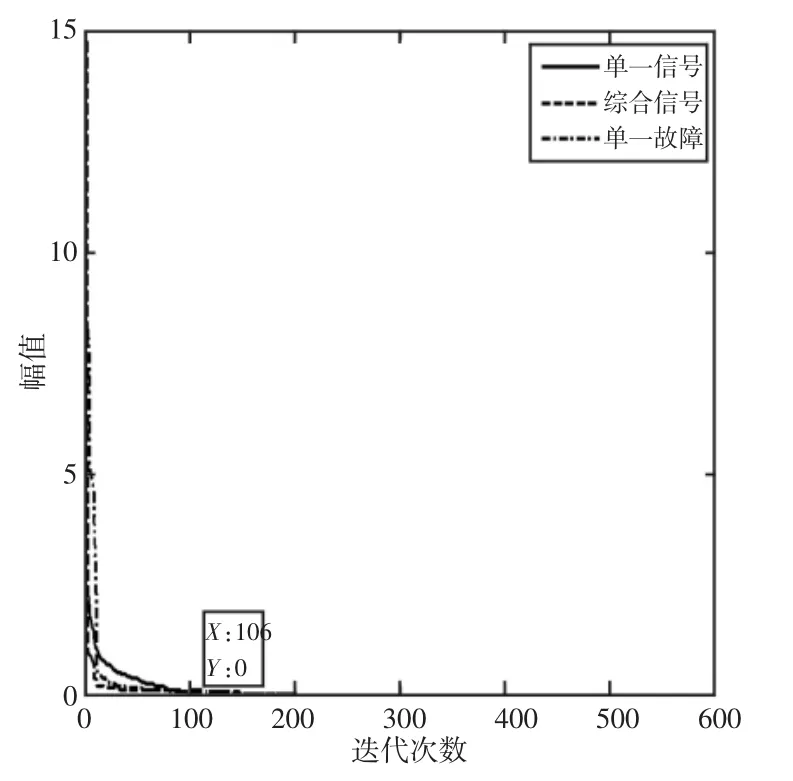
图3 按绝对值降序排列后的分解系数Fig.3 The Descending Order Decomposition Coefficient According to Absolute Value

4.2 基于不同K-SVD过完备字典的振动信号重构误差分析

采用相对误差来衡量振动信号的重构性能，相对误差是指振动信号的绝对误差与原始信号之比，其定义如下：

式中：σ—相对误差；f—原始信号；fˆ—重构信号。

相对误差越小，说明重构信号越接近原始信号，信号的重构性能越好。本次实验依然采用上述同一振动信号（OR007@6），KSVD算法中的参数设置不变，测量矩阵采用的高斯随机矩阵，重构算法采用OMP算法。图4为OR007@6驱动端振动信号在不同样本集合构造方式下的重构信号波形，其重构误差、重构时间、K-SVD字典训练时间，如表3所示。

表3 不同样本的重构性能Tab.3 The Reconstruction Performance of Different Samples

从图4和表3可以看出振动信号在单一故障信号构造的样本集合基于K-SVD算法训练所得过完备字典的字典训练时间为35.428794s，重构相对误差为1.5905e-15，相比其他两种样本集合构造所得过完备字典，其重构信号更接近原始信号，重构性能更好。故在后续实验中均采用单一故障信号构造样本集合训练获得K-SVD过完备字典。根据单一故障样本集合构造方式，分别构造正常、外圈、内圈、滚动体故障样本集合，并基于K-SVD算法训练获得对应的过完备字典，分别选取故障负载为0HP、故障直径为0.007英寸、信号长度为512的驱动端数据Normal、OR007@6、IR007、B007作为测试信号，测试信号在不同过完备字典上的重构误差，如表4所示。

图4 重构信号波形Fig.4 The Waveform of Reconstruction Signal

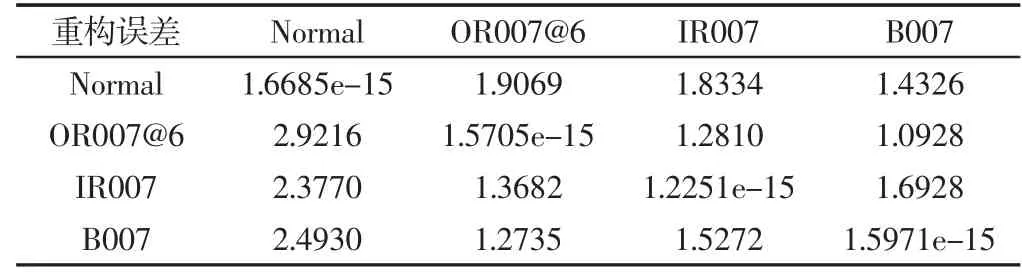
表4 测试信号在不同过完备字典上的重构误差Tab.4 The Reconstruction Error of Test Signal Based on Different Over-Complete Dictionary

从表4可以看出，只有测试信号与过完备字典在同一故障状态下时才有较高的重构精度，意味着其他故障状态下的信号不能在该字典上获得最稀疏分解，这为后续故障诊断提供了新的思路。测试信号在对应故障过完备字典上的重构误差、重构时间及K-SVD字典训练时间，如表5所示。

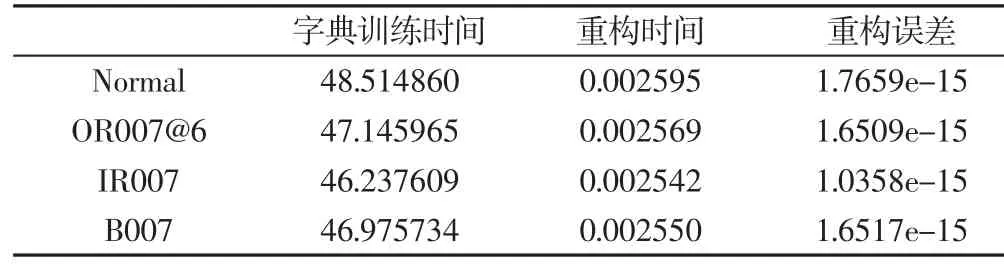
表5 测试信号在对应过完备字典上的重构性能Tab.5 The Reconstruction Performance of Test Signal Based on Corresponding Over-Complete Dictionary

从表5可以看出，测试信号在对应故障过完备字典的重构性能较好，且基于单一故障数据构造的样本集合训练所得过完备字典的字典训练时间更短，重构精度更高，重构时间更短，进一步验证了所提样本构造方法的有效性。

4.3 K-SVD过完备字典在不同采样率下的重构性能分析

为了分析滚动轴承振动信号在不同采样率δ=m/n（式中：m—压缩测量信号长度；n—原始信号长度）下的重构性能，以下进行多组实验，K-SVD算法中的参数设置如下：初始字典原子个数K=600、原子长度n=512、样本集合Y的原子个数N=1000、迭代次数J=10、稀疏表示振动信号所需最多原子个数L=10。OR007@6驱动端外圈振动信号在采样率为0.2-0.9范围内变化时的重构误差，如表6所示。

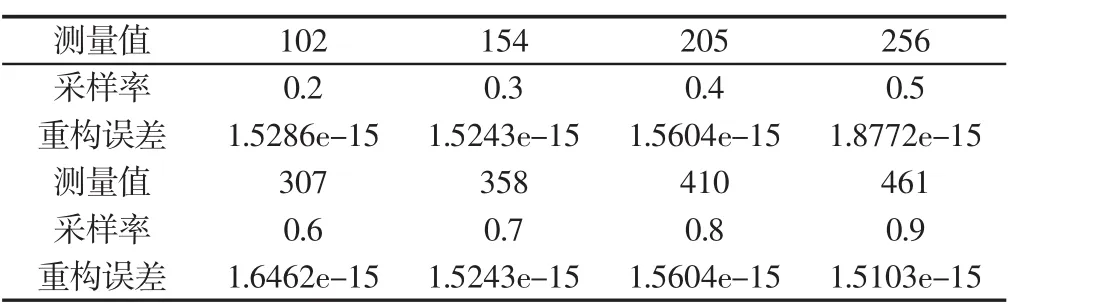
表6 不同采样率下的重构误差Tab.6 The Reconstruction Error Under Different Sampling Rate

从表6中可以看出采用单一故障信号构造样本集合后基于K-SVD算法训练得过完备字典的重构精度较高，当采样率为0.9时，重构误差为1.5103e-15，即采样率越大时重构误差越小。但是这并不适用于表6所示的情况，如表6所示。当采样率为0.2、0.3时，其重构误差分别为1.5286e-15、1.5243e-15，即在较低采样率时依然可以保证信号的重构性能，这与压缩感知理论的初衷一致，可以远低于奈奎斯特采样频率所要求的采样点数精确重构信号。为了进一步验证单一故障信号样本集合训练得到K-SVD过完备字典的重构性能。OR007@6驱动端外圈振动信号在不同采样率和样本集合构造方式下所得过完备字典的重构曲线，如图5所示。

图5 不同采样率和样本集合下的重构曲线Fig.5 The Reconstruction Curves Under Different Sampling Rate and Sample Set

从图5可以看出：在不同采样率下，单一故障信号样本集合训练所得K-SVD过完备字典的重构误差远远小于其他2种样本集合构造方式下的重构误差，说明所提样本构造方法在不丢失原始信号主要信息的情况下，仍能保证信号具有较高的重构精度。

5 结论

主要研究了K-SVD算法中样本集合的构造方式对信号重构性能的影响，通过构造单一振动数据、综合振动数据以及单一故障数据三种样本集合，将其应用于滚动轴承振动信号，分析了信号基于不同样本训练所得过完备字典的稀疏性。

仿真实验结果表明，当采样率不变时，单一信号样本集合训练所得K-SVD过完备字典的稀疏性较好，但其重构误差相对较大，字典训练时间较长。综合信号样本集合训练所得K-SVD过完备字典的重构误差和字典训练时间居中。而单一故障信号样本集合训练所得K-SVD过完备字典的重构误差非常小，且字典训练时间仅占其他两种情况字典训练时间的29.64%和37.79%。综上所述，单一故障信号样本集合训练所得K-SVD过完备字典的重构精度高、字典训练时间短、速度快，且在较低采样率下依然可以较少的采样点数高概率地重构原始信号，非常适用于滚动轴承振动信号的恢复。