基于电阻抗成像技术的金属疲劳损伤检测

孙 亮，毛汉领，黄振峰，李欣欣

（广西大学机械工程学院，广西 南宁 530004）

1 引言

无损检测技术正呈现出蓬勃发展的良好态势，其不仅为机械、冶金、电力、航空航天等工业工程的安全提供保障，同时也是可持续发展和绿色制造的有利条件。目前在金属材料的无损检测领域，红外检测、涡流检测、磁粉检测和超声检测等方法的研究已较为成熟，并且各自有其优点和局限性，在广泛的领域内发挥着重要的作用[1-3]。其中，红外检测设备昂贵，适用于导热性能较差的材料，对内部缺陷检测效果较差；涡流检测只适用于导电材料表面及近表面检测；磁粉检测只适用于对铁磁材料的表面及近表面损伤进行检测，对表面要求较高且易污染被测对象；超声检测在检测时需要使用耦合剂，可以检测内部损伤，但存在近场盲区，对近表面部分检测效果不佳，且设备相对昂贵，检测成本较高。电阻抗成像技术由美国Wisconsin大学的Swanson D.K.教授在1976年首次提出，随后在生物学、医学等领域开展了广泛的研究[4-5]。电阻抗成像技术实际上就是把电流、电压信号转化成被测对象实际阻抗（或阻抗变化）的分布过程，并以此来区分阻抗值不同的生物组织、地质或其他导电材料。根据EIT技术的相关理论，以及对金属材料疲劳损伤机理的研究，发现金属材料的损伤同样会导致其阻抗分布的变化，将EIT技术应用于金属材料疲劳损伤的检测可以弥补目前已有检测方法的不足，该方法具有低成本、易操作，可有效识别材料内、外部损伤，可实时成像等特点，希望可以为无损检测领域的研究提供一种新的思路和方法。

理论方法部分建立了金属材料损伤的电阻抗模型并介绍了电阻抗成像的基本原理；之后根据数学物理模型提取分析了在电流激励下边界电位与场域电阻率分布情况的对应关系；最后利用反投影算法进行了仿真实验分析，对45#钢材料的长方体试样进行了高周疲劳实验，实现了疲劳损伤位置的一维定位检测。

2 理论基础

2.1 金属材料疲劳损伤的数学物理模型

金属材料相邻原子间通过共价键相结合成为空间网状结构，同时内部存在大量自由电子。因为原子核的质量比电子大得多，运动速度相对极低，极化作用可忽略不计，所以金属晶体的极化主要取决于自由电子的位移。由此在微观上可以将金属晶体看作是带有正电荷的离子实组成的网状结构，其中充满了带有负电荷的自由电子[6]，无损状态下电阻率分布均匀，结构稳定，如图1所示。

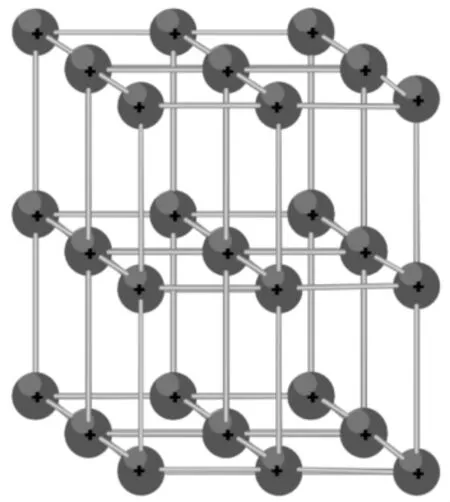
图1 金属键模型示意图Fig.1 Schematic Diagram of Metal Bond Model

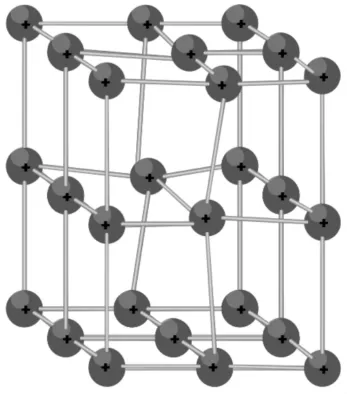
图2 晶格位错示意图Fig.2 Schematic Diagram of Lattice Dislocation

在无损状态下，金属材料的晶格有序排列，呈稳定状态。当损伤发生时，材料组织结构在外界作用下体积单元被破坏，产生位错滑移，并且在温度、载荷等外界环境因素影响下进一步扩展、聚合，直到形成更大尺度的宏观孔洞、裂纹，最终导致性能不断劣化，甚至结构失效，如图2所示。根据金属材料的电特性研究，金属的电阻率分布与材料密度变化直接相关，所以在损伤过程产生的位错滑移，以及萌生的微观裂纹和孔洞都将会导致金属材料阻抗分布的改变[7-8]。因此根据以上金属材料的微观结构和损伤机理，可以将金属疲劳损伤的阻抗特性近似为电特性模型，如图3所示。由电特性模型可知金属材料疲劳损伤电阻抗是复阻抗，其实部和虚部随驱动频率的变化而变化[9-10]。

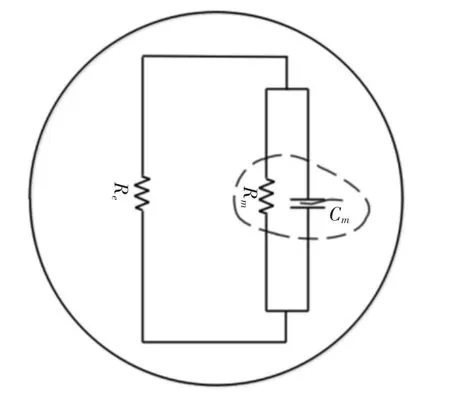
图3 电流流过损伤部位时的电特性模型Fig.3 Electrical Characteristics of Current Flowing Through Damaged Parts

KSCole在二十世纪四十年代依据上述理论提出了Cole－Cole模型，并将生物组织的电阻抗由Cole－Cole经验公式表示为[11]：

式中：ω0=2π/T0—特征频率，此频率下生物组织复阻抗可以达到最大；T0—一个时间常数；0＜α≤1。类比生物组织电阻抗模型，金属材料疲劳损伤的电阻抗模型同样可以由一个类似的经验公式来表示为：

式中：Re—无损区域的等效电阻；Rm—损伤区域的等效电阻；Cm—微观裂纹、孔隙的等效电容。

2.2 阻抗法成像技术原理

阻抗法成像的图像重建过程实际上是一个把测量电极采集到电信号转化成被测对象实际阻抗（或阻抗变化）分布的过程，如何将携带有检测对象阻抗分布信息的电信号准确转化为直观的阻抗（或阻抗变化）分布图像是研究的关键。在阻抗图像的重建过程中，利用了阻抗、电流、电压之间的联系，通常称之为“逆问题”，即已知输入输出的电信号，求解场域阻抗分布的过程。在实际研究中，同样需要对与“逆问题”对应的“正问题”进行分析，即已知输入的电信号和场域阻抗分布，求解对应的边界响应信号，如图1所示。由于阻抗图像重建过程的复杂性，简单的欧姆定律已经无法解决该问题，因此求解过程需要结合空间电磁场分布的相关理论[12]。

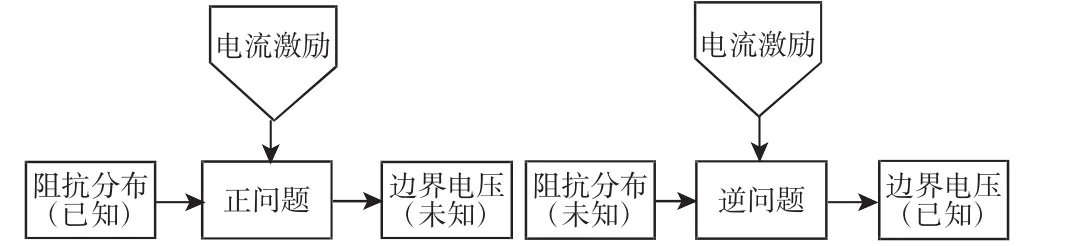
图4 图像重建中的两类问题Fig.4 Two Types of Problems in Image Reconstruction

在实际的阻抗法成像中，有如下两点假设：（1）施加的电流频率足够低；（2）被研究的物体为金属导电体。这样，在被测场域内形成的电流场就可以看作是一个准静态场（位移电流远小于传导电流）。根据欧姆定律的微分形式有：

式中：J—电流密度；σ—电导率；E—电场强度。

根据电流连续性：

电场强度E与电位φ之间有：

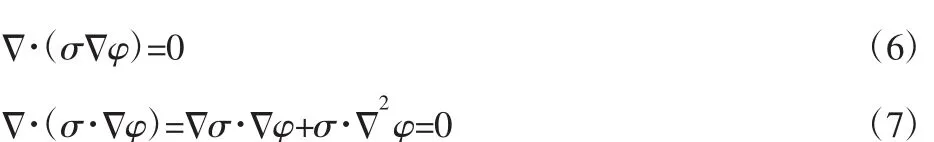
经推导代换可得：则可得泊松方程为：

式（8）中的泊松方程就是对电阻抗成像正问题的表述，当已知场域内电导率分布时，我们就可以得到场域内对应的电位分布，由电导率分布得到电位分布的过程就是阻抗成像的正问题。而在损伤检测中显然是不知道其电阻率分布情况的，所以我们需要根据场域边界测得的有效信息，逆向求得电导率的分布情况，即逆问题的研究。同时在准静态场中，电位分布函数与电导率分布函数满足拉普拉斯方程，可进行如下表述：

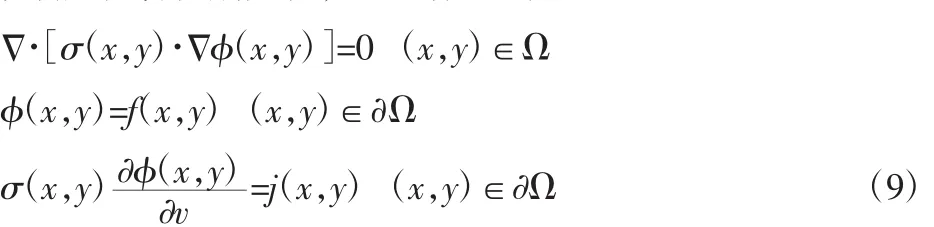
式中：∂Ω—场域的边界；f—边界电位；φ—场域电位分布函数；j—流入场域Ω的电流密度；v—场域Ω的外法向单位向量。

利用拉普拉斯方程的边界条件求解场域内的电导率分布就是最终要解决的逆问题研究。

3 有限元模型与图像重建

3.1 有元限模型

在对数学物理模型的研究中不难发现，在电流激励作用下，场域内的阻抗分布信息与边界电位的分布存在一定的敏感性关系。基于对正问题的研究，利用Matlab对以上物理模型进行有限元分析，通过电阻率的增大、位置变化和分布区域扩大等方面的分析，来考察电导率变化与边界电位的灵敏度关系。

在二维准静态场中，对于边值求解，等价变分问题可以表示为：

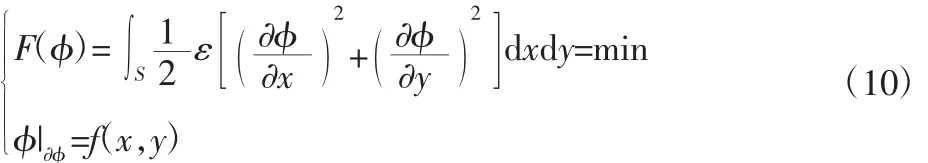
在有限元方法中，需要将连续场域剖分为有限个单元，并假定每个单元内部的电导率均为常数。如图5所示，这样在有限元模型基础上，可将式（10）中的泛函积分表示为每个单元上的面积分总和，即：

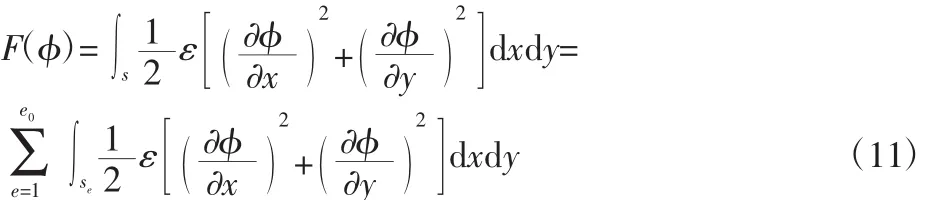
式中：se—三角单元面积；e0—场域由e0个三角单元组成。

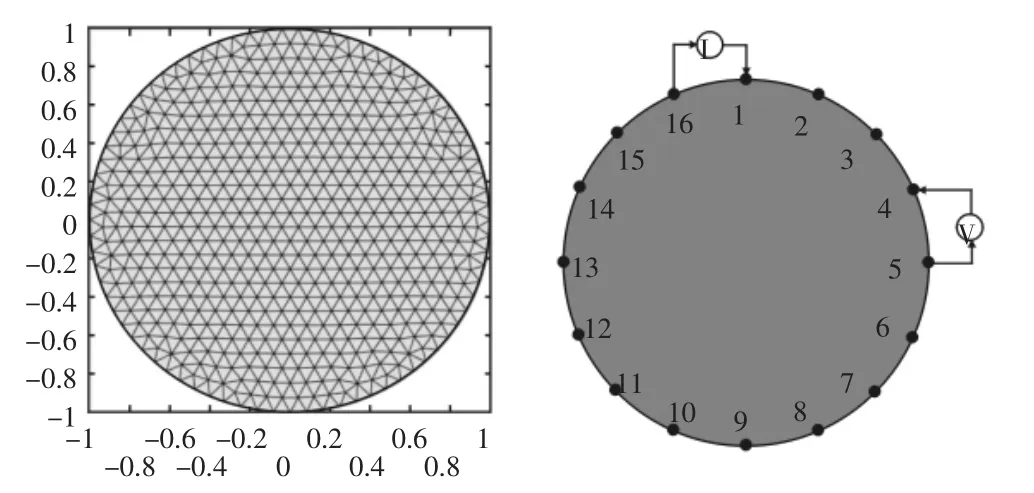
图5 有限元网格划分和测量电极分布Fig.5 Finite Element Mesh Division and Measurement of Electrode Distribution

3.2 图像重建

阻抗法成像技术是通过在被测对象表面施加低频电流，测量边界电位变化来重建对象内部的电阻率分布（变化）图像。在研究中通常根据成像目标分为动态成像和静态成像，其中动态成像以电阻抗分布的相对变化作为成像目标，如反投影法、灵敏度法等。在阻抗法成像的研究中，反投影法是一种基本的成像方法，原理可以概括为：断层平面中的某一点的密度值可看作是所有经过该点的射线投影之和的平均值。通过在场域周围布置电极，通过向场域内注入激励电流，同时在边界测得电位信息，进行不同位置的激励并获取响应信号，并将多组投影信息的叠加，从而得到电阻率分布的重建图像。

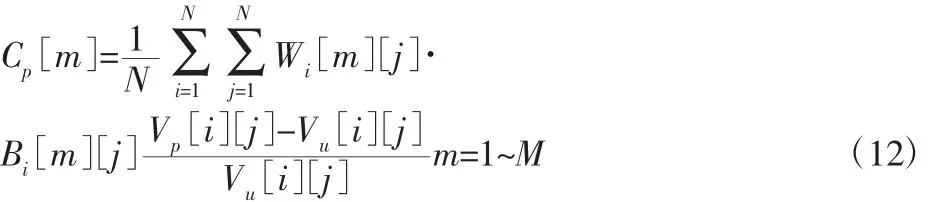
式（12）为反投影算法实际应用的一种，该方法利用等电位线划分反投影区域，通常称为等位线反投影算法。式中：Cp［m］—重建图像的像素值分布，i=1…N表示第i对电流激励电极。m=1…M—第j个元素，j=1…N表示第j对电位测量电极，表示激励电流从第i对相邻电极上注入时，第j对边界电位差投影到第m个像素上的反投影矩阵元素，当像素的电位介于第j对的两个相邻测量电极电位之间时，Bi［m］［j］为1，否则为0，Wi［m］［j］为加权系数。根据电磁学相关理论，对有限单元的电位分布求解并重建，就可以得到场域内电阻率分布的图像[13-14]。

逆问题研究中，首先要考虑的就是如何建立实际测得的边界电压变化与场域内电位分布的灵敏度关系，由于精确地灵敏度矩阵计算必须要准确的知道边界形状，电极安放位置等信息，而实际测量很难满足，即使采用标准化处理后仍然会具有病态性。采用等位线反投影算法，就可以很好的解决这一问题，将问题近似的转化成反投影关系。等位线反投影算法的有限元求解过程可分为如下几步：（1）向均匀电阻率分布的场域内注入16组激励电流，利用正问题泊松方程求解，得到电位分布信息。（2）每个电极注入电流时，每次分别提取电位值介于相邻电极之间电位的节点，形成反投影区域，得到对应16个注入电极的15组反投影关系。（考虑到实际测量时共用电极产生的接触阻抗问题，实际只提取13组。）（3）分别16次注入电流并测得电阻率变化后的16个电极电位，取其中相邻13组电极对的电位差gb，并与电阻率未变化时对应的电极对电位差ga相减得到电位差相对变化量gu，并与未变化时的电位差ga相除，得到标准变化率gn。

将标准化处理后的gn分别投影到相邻的两边界电极所夹的节点上，也就是将反投影区域上的像素值对应为gn，从而得到16组由13个电极对依次叠加的像素图，将16组图像再次加权叠加，得到最终的逆问题反投影图像。

利用有限元方法和反投影算法对损伤模型进行了图像重建，如图6所示。图6（a）、图6（b）中可以看出当损伤区域距离场域中心距离变大，重建图像的尾迹误差减少。图6（c）中当损伤区域增大为原来的两倍时，重建图像的阴影区域增大，同时损伤部位的像素值与无损区域的对比度增强。图6（d）中可以看出重建图像对多位置损伤具有良好的识别能力。结果表明反投影算法可以有效的利用边界电位信息对场域内电阻率变化情况进行表征。

图6 预置损伤区域和重建图像Fig.6 Preset Damage Region and Reconstructed Image

4 实验验证

由于金属材料在实际的交流激励下易产生电涡流、趋肤效应等问题，所以实验中采用直流电源作为激励源，同时复阻抗的问题也就简化成了只考虑实部电阻值的问题。以材质为45#钢的长方体（260×60×15）mm试样为实验对象，采用PX-20型三点弯曲疲劳试验机对试样进行单侧疲劳加载，如图7所示，进行三点弯曲疲劳加载时采用偏向一侧的方式，使得最大循环应力在试样左侧位置，从而使得试样发生不均匀损伤。根据三点弯曲应力模型，计算最大循环应力：

式中：R—最大循环应力；F—载荷；L—跨距；b—宽度；h—厚度。

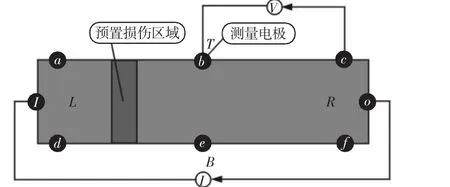
图7 测量电极分布及预置损伤示意图Fig.7 Diagram of Measuring Electrode Distribution and Preset Damage

按以上安装方式，分别采用最大弯曲应力为300MPa、320MPa、330MPa对3个同规格试样进行疲劳加载，分别对应试样标号1、2、3。每隔105次循环加载为一个加载周期，卸下试样，检验尺寸，并进行一次电阻值测量，重复加载直到试样产生肉眼可见的宏观裂纹。采用QJ-57型双臂电桥采用四端法检测其直流电阻。如图在试样左右两端输入电流，并测量得到：Rac、Rab、Rbc、Rdf、Rde、Ref，其中表示点a与点c间的测得电阻值，其余同理。

实验中为减小热电势对测量结果的影响分别从正、反两个方向通入激励电流并测量其电阻值，每次加载后重复三次正、反测量并记录数据，计算其平均值。

整体电阻相对变化率：

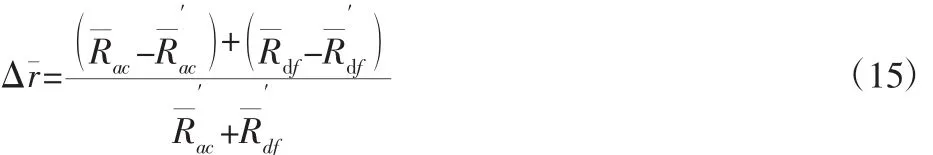
L侧电阻相对变化率：

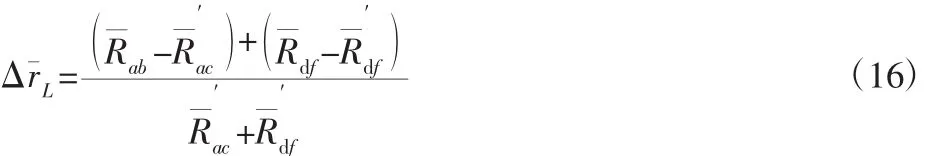
R侧电阻相对变化率：

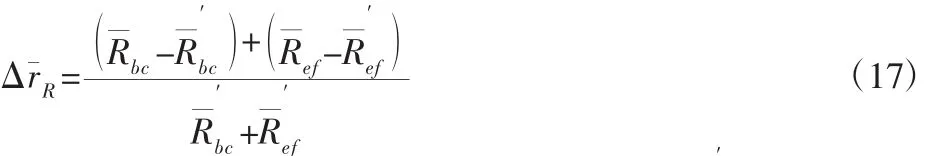
由测量数据计算得到的电阻相对变化率，如图8、图9所示。由图8可以看出可以看出试样整体的电阻值和电阻相对变化率随加载周期的增加而显著升高。由图9可以看出，随加载周期的增加，试样左侧电阻变化明显高于右侧，可以有效的检测出由疲劳损伤所引起的金属电阻率改变。

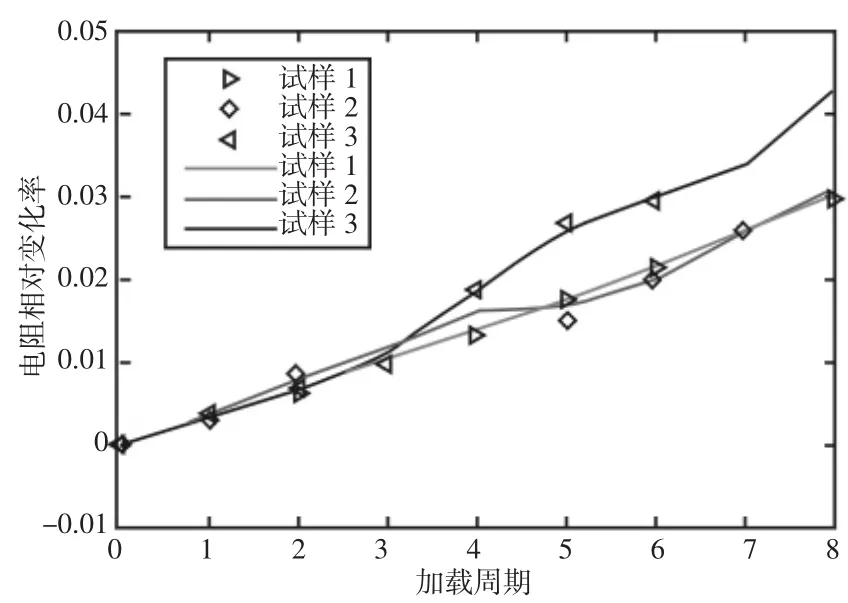
图8 整体电阻变化Fig.8 Overall Resistance Change

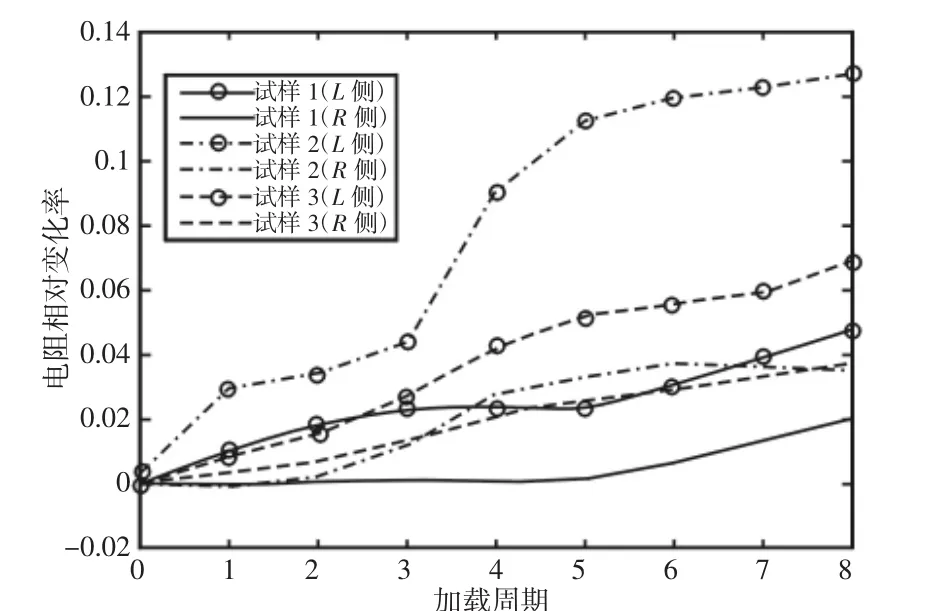
图9 单侧电阻变化Fig.9 Unilateral Resistance Change

5 结语

基于电阻抗成像技术的相关理论，深入研究了金属材料疲劳损伤机理，建立了金属材料疲劳损伤的数学物理模型和有限元模型。对逆问题的图像重建过程进行深入研究，针对以电阻抗相对变化为成像目标的动态成像算法进行了二维有限元仿真分析，结果表明动态成像方法可以有效减少测量中的系统误差，便于实现，成像速度较快，成像误差较小。通过验证性实验对长方体金属试样进行了疲劳加载和微电阻检测，实验结果表明：（1）利用金属材料的电阻抗特性对材料的疲劳损伤进行检测是切实可行的。（2）该方法可以有效地对金属疲劳损伤进行定位分析。

综上所述，将电阻抗成像技术的相关理论应用于金属材料疲劳损伤的检测能够有效的解决金属材料无损检测领域中高成本、易污染、难操作、效率低等问题。希望能够为相关领域的广大学者提供一种合理可行的研究思路和方法。