固体运载火箭级间热分离流场三维数值模拟 ①
2020-04-28朱小飞
范 健,朱小飞,李 超
(1.北京宇航系统工程研究所,北京 100076; 2.西北工业大学 燃烧、热结构和内流场重点实验室,西安 710072)
0 引言
火箭级间分离过程中受级间段结构制约及外流影响,级间分离区域内的气流流动特性会对前体和后体的气动力特性产生很大的影响,从而直接影响前后体的分离特性、分离过程及分离控制。弄清楚级间分离过程的流场结构、两级的气动力特性,获得准确的气动力参数,不仅可进行相关机理性的研究和探索,还可以为火箭级间分离方案及控制系统设计提供重要依据[1-3]。
地面实验与高空飞行实验是研究火箭级间分离的重要方法,但均存在缺点与不足,地面实验不能准确模拟高空分离环境,而高空飞行实验中获得的数据相对有限。近年来级间热分离完成了很多数值模拟研究。应用动网格技术,可实现对火箭级间热分离过程进行耦合数值模拟[4-6],但在每个计算时刻都需要生成一套新网格以适应计算域的变化,需要耗费大量的计算资源。因此,很多研究中简化计算,将流动与上下面级之间的相对运动解耦计算,其中一种解耦方式即为,仅对级间热分离过程中一些典型时刻的流场进行计算,但不作动力学计算。2003年,张文普等[7]针对某型号火箭的级间热分离过程,对从上面级发动机点火,到火箭热分离的这段时间不同时刻的流场进行了数值模拟,并对下面级发动机前封头和分离机构-柱形爆炸器进行了传热分析。2007年,黄思源等[8]应用AUSM+方法对重叠工作时间内不同时刻的流场进行了数值模拟,分别求解了非定常轴对称和非定常三维Faver平均的Navier-Stokes方程,对轴对称和三维计算结果进行了比较。2010年,张黄伟等[9]对超声速飞行弹体级间分离过程中的流场开展了数值模拟研究,得到了上下面级在不同分离状态下的气动特性,研究了弹体气动力随马赫数的变化规律。2011年,王常悦等[10]采用风洞试验和数值模拟两种手段,研究了分离过程中喷流和外流的干扰影响,关注喷流对二级气动特性的影响,并对计算和试验结果的差异进行了分析。李超等[11]采用二维动网格技术研究了级间分离过程不同排焰窗位置对火箭级间分离特性的影响,结果表明,排焰窗位置更加靠近第二级火箭时有利于多级火箭在分离过程中获得较高的相对加速度,促进多级火箭的快速分离。可以看出,目前关于火箭级间分离过程已开展了大量研究。
固体运载火箭常用的热分离方式有开排焰窗口与不开排焰窗口憋压两种。两者的共同点在于分离开始时,一级发动机在二级发动机的燃气流作用下完成减速分离过程。但不同之处在于,有排焰窗口情况下分离初始阶段级间燃气可由排焰窗顺利排出,不会在级间段形成高压;而不开排焰窗口憋压分离则会在分离初始阶段在级间段建立较高的压强,从而在分离开始时使一级发动机获得更大的初速度,有利于分离过程的快速完成。但正是由于初始阶段的憋压以及分离开始时的快速泄压,这种分离方式会对二级发动机后封头、级间段结构稳定性产生较大影响。因此,目前固体运载火箭所使用的主要分离方式为开排焰窗口分离,本文也将以这种分离方式为研究对象开展相关工作。
针对采用常规含铝17%(质量分数)复合推进剂的现代固体火箭发动机而言,推进剂完全燃烧后火箭喷流中Al2O3质量分数高达32%。如此高质量分数的凝相粒子在级间流动过程中必然与壁面发生碰撞、反弹等物理过程,从而导致分离过程中火箭前、后封头受力情况的变化,而目前国内外尚无此方面研究的公开报道。因此,本文以前期研究中的级间结构为基础[11],采用将流动与两级之间的相对运动解耦的手段,通过三维CFD模拟不同分离距离下的固体运载火箭级间流场。一方面,获得更加详细的热分离过程级间段三维流场特征;另一方面,对考虑喷流粒子影响情况下的级间段流场进行计算,分析喷流粒子对不同分离距离下火箭前后封头受力情况的影响规律。
1 物理模型及计算工况
本文所研究的固体运载火箭级间段结构如图1所示,级间段壳体上沿周向均匀分布8个排焰窗。级间热分离时,上面级发动机点火,高温高压燃气冲击下面级发动机的前封头,反射后由排焰窗流出,在一定时间间隔后,级间分离,两体产生相对运动。
计算区域为对称结构,计算时只需计算1/4区域,计算区域及网格划分见图2。为了提高计算速度及精度,在网格划分时对所建立的计算模型进行合理分区,并划分结构网格,在下面级发动机前封头和上面级发动机后封头处进行网格加密。
计算模型中边界条件如图1所示,其中入口边界条件为压力入口,压力大小按照上面级燃烧室燃气总压给定,具体压力值列于表1中,表中最后一列为不同分离距离所对应的时刻。出口为压力出口(图1),出口参数按照海拔20.954 km处大气参数给定,压力5500 Pa,温度为217 K。当分离距离大于零时,分离处也设置为压力出口(图1)。
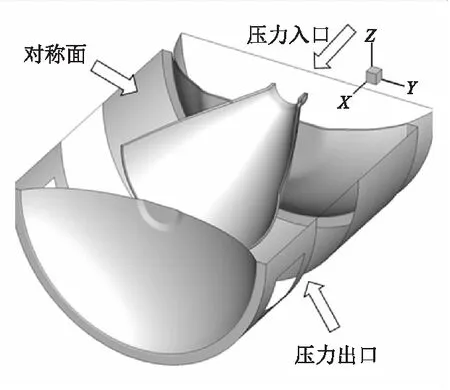
图1 物理模型
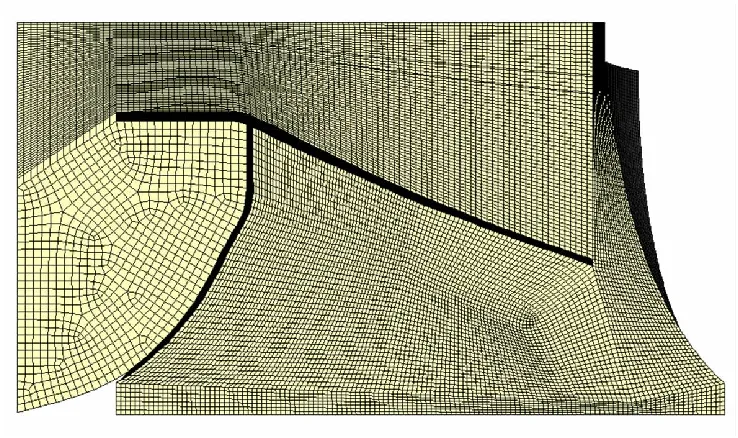
图2 计算区域及网格划分
本文所有计算工况均分为考虑和不考虑凝相颗粒两种情况。由于一般固体推进剂含铝质量分数为17%,完全燃烧后Al2O3液滴的质量分数约为30%,Al2O3液滴的尺寸主要集中于亚微米到几十微米之间[12]。因此,本文计算中按照Al2O3物性参数给定凝相颗粒参数,密度3300 kg/m3,质量流率为燃气质量流率的30%。颗粒粒径分布为平均粒径5 μm,最小粒径1 μm,最大粒径10 μm的正态分布。研究中认为燃气为理想气体,不考虑不同气相组分之间的化学反应,燃气总温均为3530 K,平均分子量为29.35 g/mol,燃气的比热容保持不变。

表1 计算工况
2 控制方程
2.1 气相控制方程
对于m组分,气相的质量守恒方程:
(1)

(2)
由于离散的液滴成分只有水一种介质,即δm1=1,所以气相的质量守恒方程最终可以写为
(3)
气相的动量守恒方程为
(4)

同样,气相能量方程可以写为
(5)
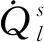
(6)
式中T为气体的温度;hm为m组分的比焓;K为气体的热导率,K=(μcp)/Pr;Pr为湍流普朗特数。
2.2 离散相模型
凝相颗粒的运动轨迹是通过求解在拉格朗日坐标系下对凝相颗粒所受作用力的微分方程得到的。凝相颗粒的力平衡方程如下:
(7)
(8)
式中FD(u-up)为凝相颗粒的单位质量曳力;u为流体相速度;up为颗粒相速度;μ为流体动力粘性系数;ρ为流体密度;ρp为凝相颗粒密度;dp为凝相颗粒直径;Re为相对雷诺数;CD为曳力系数。
凝相颗粒的力平衡方程中Fx代表着凝相颗粒所受的附加合力,这些作用力主要由凝相颗粒加速度力和流体不均匀力组成,其中加速度力由视质量力和Basset力组成,是凝相颗粒在加速运动时作用于凝相颗粒上的附加力;而流体不均匀力是指由于流体的不均匀性而作用于凝相颗粒上的附加力,包括压力梯度力、热泳力、马格努斯力和萨夫曼滑移-剪切升力。凝相颗粒在高温高压的两相流场中受力情况十分复杂,本文仅考虑Basset加速度力、压力梯度力、热泳力、马格努斯力及萨夫曼升力,其他力由于量级相对较小在运动模型中不予考虑。
2.3 物理模型假设条件
固体火箭级间热分离流场结构极为复杂,流动过程为含有化学反应的三维两相湍流流动,此时考虑所有流场因素进行模拟难度较大。因此,本文研究中对该过程进行了合理简化,数值模拟中采用如下假设:
(1)流动为三维准定常流动;
(2)燃气为理想气体,满足理想气体状态方程,p=ρRT;
(3)凝相颗粒仅为惰性Al2O3颗粒,在级间段流场内不存在化学反应过程;
(4)不考虑流动过程中由于凝相颗粒相互碰撞导致的凝相颗粒粒径变化(液滴破碎、液滴融合);
(5)在固体壁面上对颗粒采用反弹模型,仅考虑气相拖曳力对颗粒的作用,忽略重力、升力等其他作用力。
3 分离计算结果
3.1 计算模型验证
为证明本文计算模型的正确性及合理性,选择分离距离0.2 m情况下的工况(3#工况)作为典型工况,与文献[11]中特征点处的压强、速度计算结果进行对比校验。验证中,沿轴线方向分别取与喷管入口截面距离为1/3、1/2及2/3计算区域长度处的点为特征点,对计算结果进行对比,如表2所示。可以看出,本文建立的模型具有较高精度,可用于火箭级间热分离过程的三维流场数值仿真。
3.2 级间段三维流场计算结果
为对比分析凝相颗粒对级间段流场结构及其分布特征的影响,首先以3#工况作为标准工况,给出不考虑凝相颗粒情况下级间段对称面上的压强、温度以及马赫数流线计算结果,如图3所示。图4~图6分别给出了考虑凝相颗粒的级间结构内对称面上的流场压强、温度云图及马赫数流线图,表3给出了考虑凝相颗粒与不考虑凝相颗粒情况下级间段典型面上的压强及平均受力大小。
由级间段流场分布云图可以看出,添加凝相颗粒与否并不会对级间段流场的结构及其分布特征产生明显影响,这是因为本文计算中所选择的凝相颗粒粒径为1~10 μm,该粒径下的凝相颗粒在流动过程中具有很好的随流性,其对流场的影响作用主要表现在由凝相与气相间温度、速度滞后所导致的两相流动损失,而对于对级间段流场的特征并不会产生明显影响。
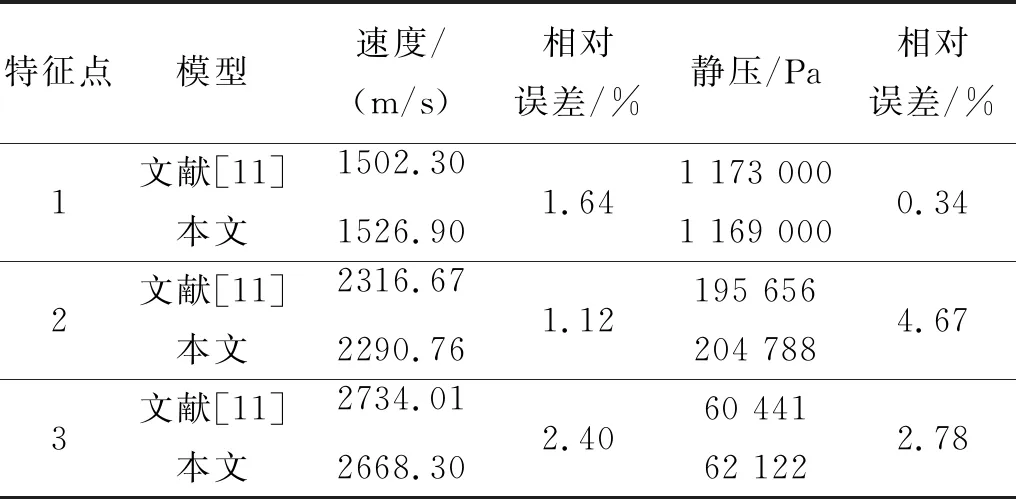
表2 模型验证

表3 级间段特征面压强和平均受力情况
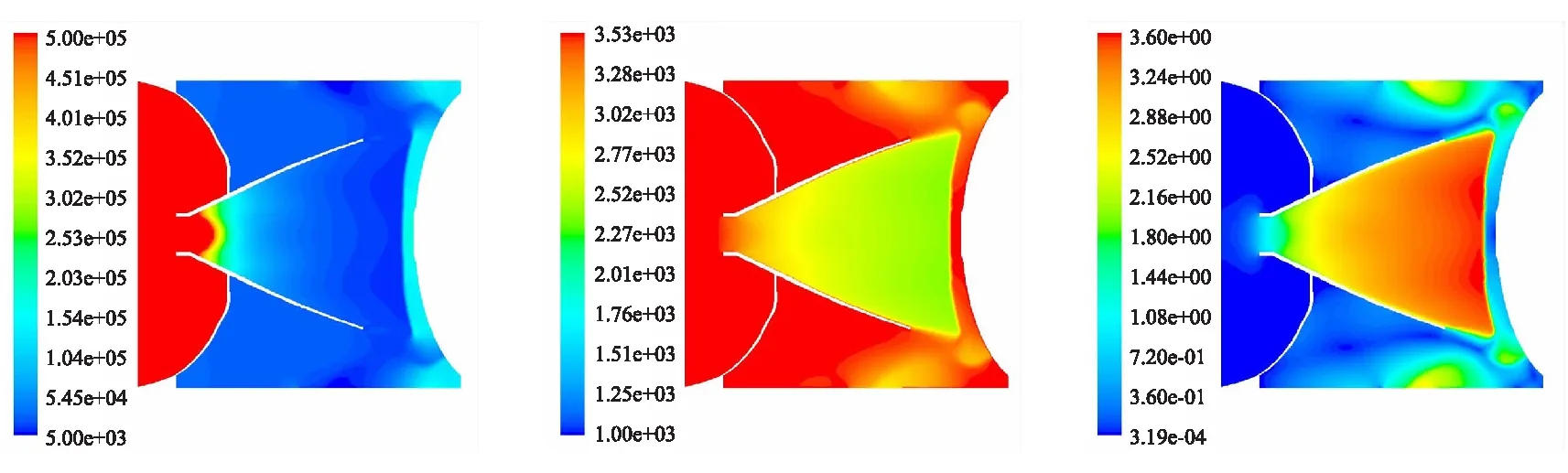
(a) 压强云图(单位:Pa) (b)温度云图(单位:K) (c)马赫数云图
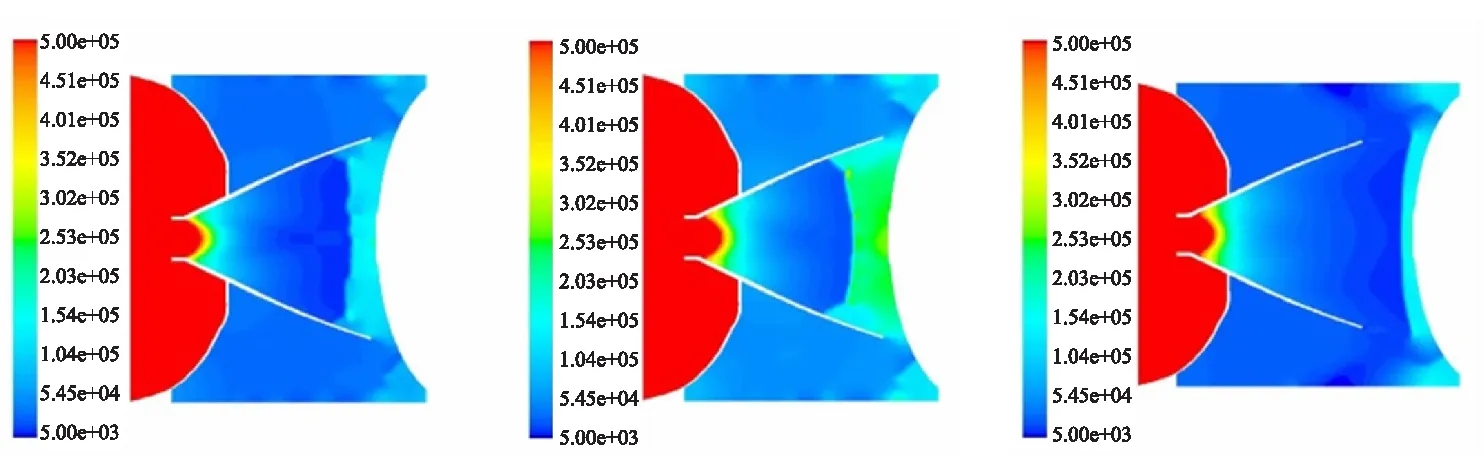
(a) 1#工况 (b)2#工况 (c)3#工况

(d)4#工况 (e)5#工况 (f)6#工况 (g)7#工况
对比本单位前期研究中级间流场的二维计算结果[11],可以看出考虑凝相粒子条件下的三维级间段流场发展规律及特征与二维情况下基本相同,即在级间热分离初期,上面级发动机点火后,高温燃气迅速充满级间段,导致级间区域内压力迅速升高,使喷管处于过膨胀状态,在喷管扩张段出现激波诱导的边界层分离现象,如图4(a)、(b)所示。随着上面级发动机燃烧室总压的快速升高以及两体分离距离的增大,位于喷管内的激波被推出喷管,喷管扩张段的流动分离也随之消失(图4(c))。随后,这道激波一直被燃气射流推到下面级发动机的前封头附近(图4(d)~(g)),然后燃气射流改变流动方向,由排焰窗和分离面流出。
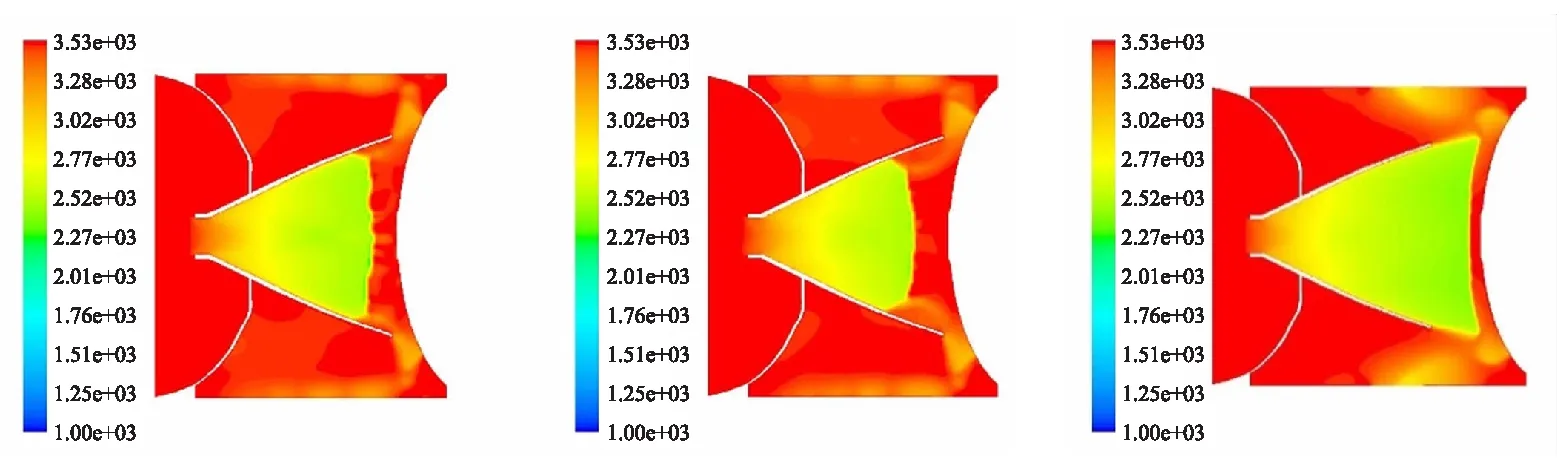
(a) 1#工况 (b)2#工况 (c)3#工况

(d)4#工况 (e)5#工况 (f)6#工况 (g)7#工况
从图5可看出,在级间分离开始时刻,由喷管排出的燃气在碰撞到级间段壁面后被滞止,级间段内充满了高温燃气。而随着分离距离的增大,级间段靠近上面级后封头部分的高温燃气得以从分离面排出,如图5(d)~(g)所示。而在整个分离过程当中,由于下面级火箭前封头附近正激波的存在,在本文所计算的分离距离内,此处一直为高温滞止区。这一过程也与二维流场计算结果相符[11]。
图6给出了分离过程级间段的马赫数流线图,级间段流场变化剧烈,除了存在复杂的激波、膨胀波、流动分离和边界层分离等现象外,还存在的明显的涡旋结构。可以看出级间段内的涡旋结构主要出现在级间段结构狭窄、流速较低、高温燃气难以及时排出级间段的区域。
图7给出了分离过程级间流场的凝相颗粒迹线分布情况,可以看出在分离时刻,级间区域内颗粒轨迹分布杂乱,在整个级间区域具有分布,如图7(a)、(b),此时级间段过多的凝相颗粒分布可能会对级间热防护带来一定的难度。

(a) 1#工况 (b)2#工况 (c)3#工况
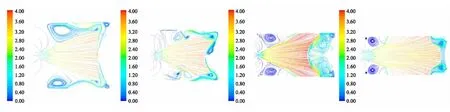
(d)4#工况 (e)5#工况 (f)6#工况 (g)7#工况
而随着分离距离增大,大部分凝相颗粒逐渐从分离面排出图7(c)、(d)。当分离距离进一步增大,几乎所有凝相颗粒都可由分离面排出,而不会对上面级火箭后封头产生影响。与图6中级间段流场的流线分布图明显不同,图7中颗粒轨迹并不会存在明显的涡旋结构,这是因为相比于气相,高速流动的凝相颗粒具有更大的惯性,当遇到壁面折转后,其流动状态更加难以发生改变。
3.3 凝相颗粒对级间段影响分析
图8给出了在考虑凝相颗粒和不考虑凝相颗粒情况下,下面级前封头和上面级后封头的平均压强随分离时间变化的曲线。可见,在级间分离过程中,下面级前封头的平均压强始终高于上面级后封头,并且两者间压强差随着分离的进行整体呈增大趋势。随着分离时间的增加,下面级前封头上的平均压强在振荡后持续提高;上面级后封头上的平均压强前段缓慢上升、后段迅速下降,并逐渐趋近于环境压强。此外,还可以看出添加凝相颗粒后,下面级前封头表面压强略微有所降低,上面级后封头表面压强在分离前期略微上升,随后低于纯气相,但在分离后期也逐渐趋于环境压强,在本文研究参数范围内,凝相颗粒对上面级后封头和下面级前封头压强的影响并无明显规律。这是因为,一方面凝相颗粒与燃气之间的速度滞后和温度滞后所导致的两相流动损失会使燃气的做功能力降低,从而引起前、后封头压强的下降,而另一方面,相比于高温燃气的撞击壁面过程,凝相颗粒与壁面碰撞时会有更多的动能传递给固体壁面,从而引起壁面压力的上升。加之分离过程级间段流场结构复杂、变化剧烈,各种影响相互耦合,还需开展更加具有针对性的研究以揭示各个因素对分离过程的影响机理。

(a) 1#工况 (b)2#工况 (c)3#工况

(d)4#工况 (e)5#工况 (f)6#工况 (g)7#工况

图8 分离时间-压强曲线
图9给出了在考虑凝相颗粒和不考虑凝相颗粒情况下,下面级前封头和上面级后封头受力随分离时间变化的曲线,其总体趋势与平均压强曲线图相似。在分离初期,下面级前封头由于受到上面级射流的冲刷作用,其表面受到约220 kN的力,该作用力随着分离的进行整体呈增大趋势。
由于分离初期级间分离距离小,上面级射流无法及时排出级间段,因而上面级后封头会受到射流回流的冲刷作用,该作用力在分离初期缓慢增大,但随着分离距离的增大,射流回流作用减弱,在分离后期,上面级后封头受力逐渐趋于零。
总结看来,随着分离时间增加,下面级前封头表面受力在振荡后持续提高;上面级后封头表面受力前段缓慢上升、后段迅速下降,并逐渐趋近于零。
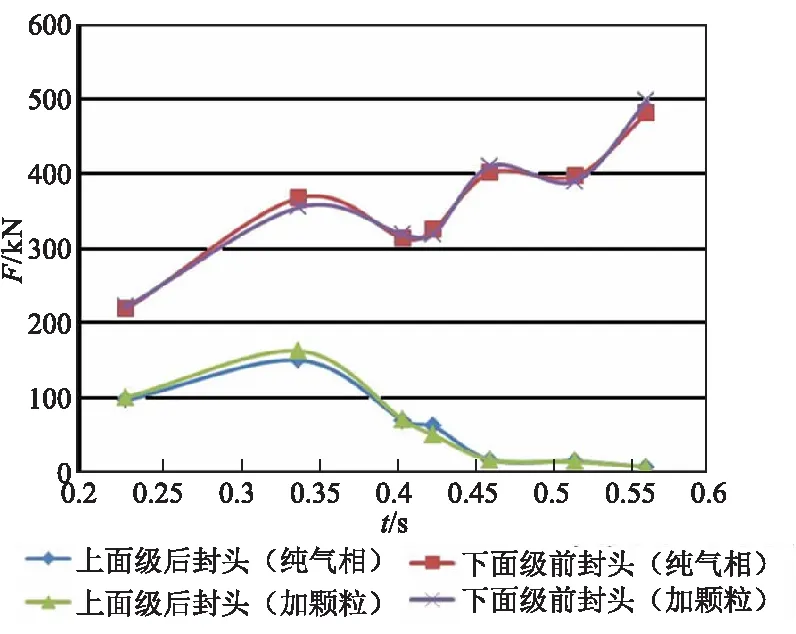
图9 分离时间-受力曲线
4 结论
本文对考虑和不考虑凝相颗粒影响的多级火箭级间热分离过程进行了三维流场数值仿真,得到以下结论。
(1)通过将流动与两级之间的相对运动解耦,建立的固体运载火箭级间分离模型具有较高的精度,可用于级间分离过程流场特性的研究。
(2)火箭级间分离过程中,级间流场变化剧烈,级间段流场存在激波、膨胀波、流动分离、边界层分离和涡旋等复杂的流动现象。
(3)在一定分离时序内,随着分离时间的增加,下面级前封头上的平均压强在振荡后持续提高;上面级后封头上的平均压强前段缓慢上升、后段迅速下降,并逐渐趋近于环境压强。
(4)在本文研究条件下,凝相颗粒对上面级后封头和下面级前封头压强的影响并无明显规律。
