一种基于双目视觉的卫星相对位姿测量方法*

邓 爽， 王 波， 董秋雷,3*

0 引 言

在进行卫星的对接任务时，对卫星的位姿测量是其中非常重要的一环.在对卫星进行位姿测量后，对接目标可以依据卫星位姿调整自己的姿态进行精准对接.针对合作型卫星，可以在卫星上加装定位跟踪装置，让对接目标能自动追踪卫星的位姿.非合作型卫星不一定存在定位追踪装置，所以只能通过对接目标的摄像头拍摄到的图片对卫星进行定位.由于卫星表面一般覆盖着聚酰亚胺的高性能聚合物材料与金属材料复合而成的薄膜，这种薄膜是反光材质，在太空背景中对接目标打出的单一光源下会出现复杂的光照纹理，并且在不同角度观测下纹理会不同.传统视觉定位方法依赖SIFT特征点[1]的提取与匹配，然而在这种背景条件下会产生大量错误匹配点.卫星作为一种特殊的设备，一般在正表面都会存在对接环和安装部件，目前关于卫星位姿测量的研究主要针对卫星上的特殊装置.

近年来，研究者开展了大量有关视觉位姿测量的研究工作[2-5].文献[3]利用双目相机拍摄到的卫星图像提取卫星对接环和十字力架，并直接由对接环和十字力架的交点进行双目重建计算卫星位姿.文献[4]利用单目摄像头拍摄到的对接环进行重建，并依据已知的卫星轮廓边长筛选得到三维对接环模型，并依此得到卫星姿态.文献[5]同样利用单目摄像头拍摄到的卫星对接环进行重建，并利用已知的对接环半径筛选得到对接环三维信息.文献[3-5]都利用了卫星不普遍存在的特征，比如十字力架，已知的轮廓边长和对接环半径.对于非合作型卫星，这些已知信息是无法得到的.除此之外，这些方法都利用简单的Canny边缘检测方法[6]提取对接环椭圆特征.由于卫星表面是反光材质，在单一光源下会产生复杂的纹理，这种复杂纹理会影响Canny边缘检测算子，从而无法得到精确的对接环椭圆.文献[4]利用了卫星的轮廓信息，然而在卫星距离目标较近时，卫星的轮廓会无法观测.

基于上述问题，本方法在双目相机拍摄的图像中利用卫星普遍存在的特征(对接环外环，卫星面板标志点)进行位姿测量.本方法为解决卫星表面复杂的光照纹理影响对接环识别的问题，利用了一种先进的椭圆识别方案.由于卫星距离对接目标距离较近时，卫星面板标志点已无法检测，而这时卫星表面的复杂纹理影响较小，所以利用快速的特征检测算子ORB特征[7]进行图像的特征点检测和匹配，以计算卫星的位姿.除此之外，此方法还利用光流追踪法[8]和卡尔曼滤波器[9]优化姿态结果，进一步提升姿态估计的精确度，让卫星和对接目标实现更精确的对接.

1 问题描述与定义

已知双目相机系统中左、右相机的内参数矩阵分别为Kl和Kr，双目摄像头的畸变参数矩阵Dl和

Dr，以及双目相机之间的旋转矩阵R和平移向量t，则双目相机的摄像机矩阵Pl和Pr为：

(1)

双目相机基础矩阵F为：

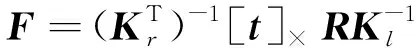
(2)

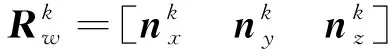
2 整体流程

图1 本文方法流程图Fig.1 The flowchart of the proposed method

的情况，则当前帧会检测和匹配ORB特征点以备用.若当前帧不能看见面板标志点，则依据左相机当前帧图像检测到的ORB特征点和左相机上一帧图像ORB特征点的匹配来进行位姿测量，并且会利用检测到的对接环外环椭圆优化位姿结果.对于非初始帧都会在计算完卫星位姿后利用卡尔曼滤波器优化位姿结果.

3 卫星特征检测

3.1 对接环外环检测

图2为卫星面板示意图.由于卫星面板为反光材质，对接环外环边缘会被高光覆盖，所以需要从高光区域中正确检测出椭圆.本方法采用文献[10]提出的高稳定性椭圆检测方法.此方法首先对图像计算每个像素的梯度垂直方向，作为像素的边缘方向，并将边缘方向能形成弧线的区域记为弧线像素区域，拟合出弧线像素区域的局部直线线段，记为弧支撑线段.然后连接潜在地属于同一椭圆的弧支撑线段并分组，得到弧支撑线段组.之后采用两种方法拟合初始椭圆：选择具有显著椭圆形状特征的弧支撑线段组拟合初始椭圆和全局搜索能匹配的多个弧支撑线段组拟合初始椭圆，通过初始椭圆在参数空间的聚类将初始椭圆合并得到椭圆候选集.最后在椭圆候选集中剔除质量不高的椭圆并对剩下椭圆的参数进行优化.

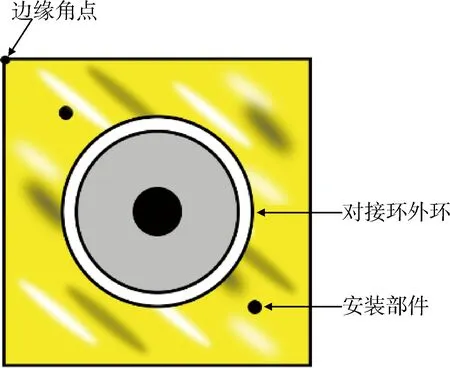
图2 卫星面板示意图Fig.2 The diagram of the satellite panel

3.2 面板标志点检测

如图2所示，卫星面板普遍存在的面板标志点主要为边缘角点和安装部件中心点.

1)边缘角点提取：首先利用霍夫直线法[11]检测两幅图中直线参数累加器值最大的各4条直线，作为卫星面板轮廓的4条边.然后计算4条边相交的4个交点.在左相机图像中选定4个交点的其中一个点作为面板标志点pl，并利用基础矩阵计算此点在右相机图像中对应的对极线lr：

lr=Fpl

(3)

并在右相机图像4个交点中选取离lr最近的点作为面板标志点pr.

2)安装部件中心点提取： 由于安装部件一般是较小的黑色斑点，所以利用加入颜色筛选，面积筛选和曲率筛选的斑点检测法[12]检测两幅图中的候选斑点.在左相机图像的候选斑点中选取一个作为面板标志点pl，与上述一样计算此点在右相机图像中对应的对极线lr，选取右相机图像中距离lr最近的候选斑点，作为右相机图像面板标志点pr.

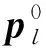
4 卫星位姿测量

4.1 椭圆和点匹配重建

(4)

然后将ATA进行特征分解得到特征值λi(i=1,2,3,4)和对应的特征向量ξi(i=1,2,3,4).从λi中选取最小值λmin=min (λi)，并得到λmin对应的特征向量ξmin，则：

(5)

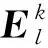
为：

(6)

在左相机坐标系下，两个椭圆锥面的圆截面单位法向量分别为：

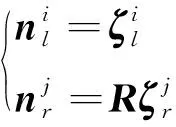
(7)

(8)

最后得到卫星位姿为：

(9)

4.2 ORB特征点匹配重建

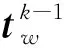
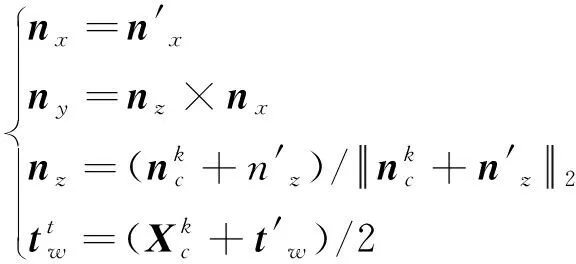
(10)

为了得到此帧ORB特征点的三维坐标，首先对左相机图像和右相机图像分别进行ORB特征点检测，将两幅图像的ORB特征点通过暴力匹配得到初始匹配特征点.然后对所有初始匹配特征点进行双目重建得到初始匹配点三维坐标.由于ORB特征点在卫星面板上，依此条件筛选三维点，并将三维点和与之对应的图像ORB匹配点一并保存用于下一帧的处理.

4.3 卡尔曼滤波模型

5 仿真分析

5.1 实验条件

为模拟卫星在太空中对接场景，本实验在一个密闭黑暗空间中进行.卫星为模拟人造卫星，并被固定在机械滑轨装置的滑块上.双目相机被固定在滑轨一端，正向面对卫星面板.双目相机中间有单一光源打向卫星面板.在实验过程中，卫星将从距离双目相机中心7 m处匀速运动到距离双目相机中心3 m处，且卫星在移动过程中做绕卫星中心轴匀角速度自旋转运动.这样能检验定位方法在卫星位移和旋转上的估计精度.双目相机会在每隔5 s采样一帧图像对，每两帧之间卫星移动大约5 cm，旋转10°.双目相机会将采样的图像对输入个人电脑以供计算位姿.

本实验采用的个人电脑型号为MECHREVO NX6，处理器为Intel i7-8700，内存为16 GB，操作系统为Windows10 64位.本方法采用c语言编写，并用Visual Studio 2017执行.

5.2 定位精度分析

表1显示了卫星从距离双目相机中心7 m处匀速运动到距离双目相机中心3 m处所有帧的位姿(距离和旋转角)平均误差，以及前后帧间相对位姿的平均误差.由于当卫星在距离双目相机较远时比距离双目相机较近时特征纹理更为模糊，所以卫星位姿测量精度在卫星距离双目相机较远时会更差.所以在实验中，本方法不仅测量所有帧位姿的平均误差之外，还会测量在卫星距离双目相机不同距离阈值内的位姿平均误差.图3和图4分别展示了卫星在7～5 m间和在5～3 m间真实距离和计算距离的逐帧对比折线图.图5和图6分别展示了卫星在7～5 m间和在5～3 m间真实旋转角和计算旋转角的逐帧对比折线图.表2展示了卫星在7米到5米间和在5米到3米间位姿平均误差和前后帧间相对位姿的平均误差.从表1中可以看出本方法在估计卫星对接过程中的位姿中能够保证较高的精度，并且前后帧的相对位姿估计准确且稳定.图3～图6和表2说明了卫星距离双目相机越近，位姿测量会越准确.在卫星距离对接目标较远时对接目标只需要了解卫星的大致方位，所以此时对卫星位姿的精度要求不高.

图3 7～5 m阈值内的真实距离和计算距离Fig.3 The real distance and the calculated distance in 7～5 m

表1 卫星位姿测量的平均误差Tab.1 The average errors of satellite pose measurement

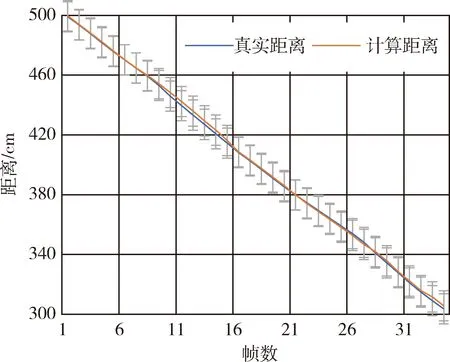
图4 5～3 m阈值内的真实距离和计算距离Fig.4 The real distance and the calculated distance in 5～3 m

图5 7～5 m阈值内的真实角度和计算角度Fig.5 The real angles and the calculated angles in 7～5 m

图6 5～3 m阈值内的真实角度和计算角度Fig.6 The real angles and the calculated angles in 5～3 m

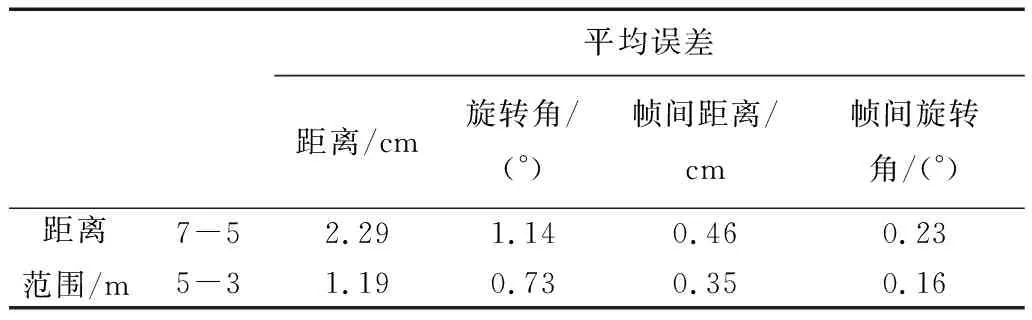
表2 在不同距离阈值中卫星位姿测量的平均误差Tab.2 The average errors of satellite pose measurement under different distance thresholds

5.3 运行时间分析

表3显示了卫星从距离双目相机中心7 m处匀速运动到距离双目相机中心3 m处所有帧位姿测量的平均运行时间.由于当卫星在距离双目相机较远时在图像中显示区域较小，所以位姿测量运行时间在卫星距离双目相机较远时会更短.所以在实验中，本方法不仅测量所有帧卫星位姿测量的平均运行时间之外，还会测量在卫星距离双目相机不同距离阈值内位姿测量的平均运行时间.表4展示了卫星在7～5 m间和在5～3 m间位姿测量的平均运行时间.表3说明了本方法运行较为高效.在每一帧位姿测量的过程中，主要花费时间集中在处理图像和检测椭圆中，其余算法运行时间较短.表4说明了在卫星距离双目相机距离越近，位姿测量平均时间会越长，其中检测卫星对接环椭圆和标志点的运行时间显著加长.但是这个运行时间仍大幅小于每两帧之间的采样间隔时间，所以本方法的运行时间不会影响对接任务的效率.

表3 卫星位姿测量的平均运行时间Tab.3 The average running time of satellite pose estimation

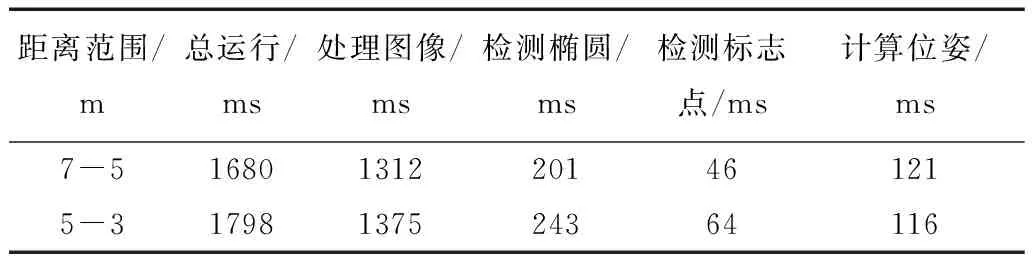
表4 在不同距离阈值中卫星位姿测量的平均运行时间Tab.4 The average running time of satellite pose estimation under different distance thresholds

6 结 论

由于太空环境中光源单一，且卫星表面一般为反光材质，在对接任务中对卫星进行准确的位姿测量是较为困难的.本文提出了一种高效且稳定的卫星双目位姿测量方法.本方法利用卫星固有的特征(对接环以及面板标志点)进行位姿测量，并且引入ORB特征点、光流追踪法和卡尔曼滤波模型以增强算法鲁棒性.仿真实验结果验证了本文方法的有效性.